Table 1. Complex network statistics commonly used in this work.
| Measure | Definition | Interpretation |
|---|---|---|
| Node degree | 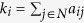 |
Number of edges connected to a given node i. Nodes with relatively high values of k are called hubs |
| Shortest path length |
 where ri↔j is the shortest path between i and j where ri↔j is the shortest path between i and j
|
The number of edges encountered in the shortest path between node i and j |
| Characteristic path length | 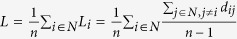 |
Measure of network integration. Small values identify strongly integrated networks |
| Clustering coefficient |
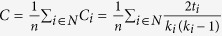 , with , with 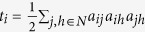
|
Measure of fine-grain network segregation. It counts the average number of triangles t (3-node fully connected graphs) present in the network |
| Modularity |
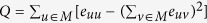 , where M is a partition of V (whose elements are called modules) and euv is the proportion of links that connect nodes in module u with nodes in module v , where M is a partition of V (whose elements are called modules) and euv is the proportion of links that connect nodes in module u with nodes in module v
|
It evaluates the tendency of the network to be reduced in independent (or scarcely dependent) modules |
| Betweenness Centrality |
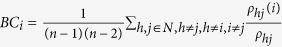 , where ρhj is the number of shortest paths between h and j, and ρhj(i) is the number of shortest paths between h and j that pass through i , where ρhj is the number of shortest paths between h and j, and ρhj(i) is the number of shortest paths between h and j that pass through i
|
It is the amount of shortest paths that pass through the node i. It roughly indicates how much information burdens the node i |
| Small-worldness |
 , where Cr and Lr are the randomized version of the original network; S >1 denotes small-world networks , where Cr and Lr are the randomized version of the original network; S >1 denotes small-world networks |
It determines how much the network is a small-world network. |
All formulas are referred to a (undirected) graph 〈V, E〉, with |V| = N, opportunely described by the adjacency N × N-matrix A = aij where aij = 1 if and only if there exist the element (i, j) in the set E and 0 otherwise.
