Detecting hybridization using ancient DNA

Abstract

It is well established that related species hybridize and that this can have varied but significant effects on speciation and environmental adaptation. It should therefore come as no surprise that hybridization is not limited to species that are alive today. In the last several decades, advances in technologies for recovering and sequencing DNA from fossil remains have enabled the assembly of high-coverage genome sequences for a growing diversity of organisms, including many that are extinct. Thanks to the development of new statistical approaches for detecting and quantifying admixture from genomic data, genomes from extinct populations have proven useful both in revealing previously unknown hybridization events and informing the study of hybridization between living organisms. Here, we review some of the key recent statistical innovations for detecting ancient hybridization using genome-wide sequence data, and discuss how these innovations have revised our understanding of human evolutionary history.

For more than two decades after the first DNA sequences were isolated from ancient remains (Higuchi et al. 1984; Pääbo 1985), the field of ancient DNA was limited to cloning or PCR-based interrogation of one or a few genetic loci. Such data can be useful for studying some aspects of past demography such as population migrations and bottlenecks (Hawks et al. 2000; Wang et al. 2000). For detecting subtle signals of admixture, however, genome-wide data sets are necessary. These data are becoming routinely available from ancient remains via high-throughput sequencing (Metzker 2010) of DNA. Beginning with the retrieval of 13 Mb of the mammoth genome (Poinar et al. 2006) and portions of the Neanderthal genome (Green et al. 2006; Noonan et al. 2006), a variety of approaches have been developed to extract DNA and make it available for direct sequencing, ushering in the new era of paleogenomics (Shapiro and Hofreiter 2014).

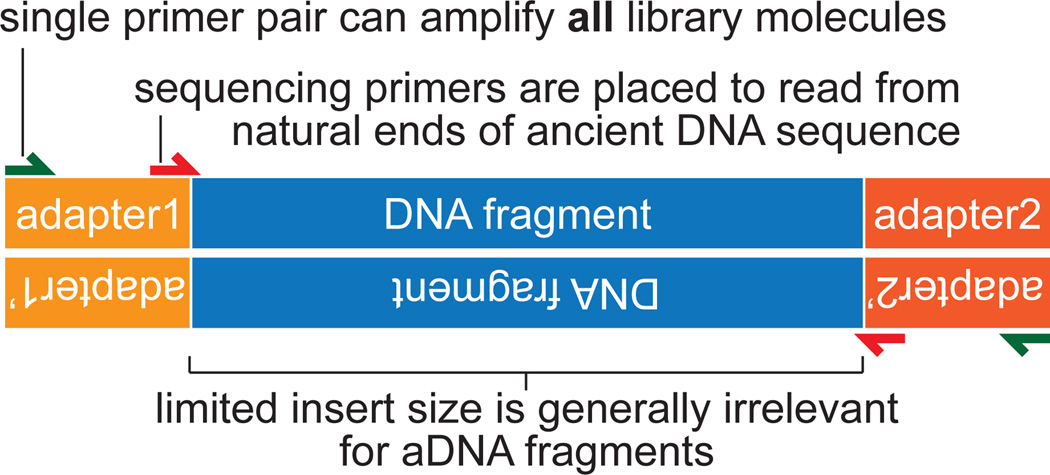
The field of ancient DNA has realized enormous benefits from the gains in efficiency of high-throughput sequencing (HTS). First, HTS libraries and the machines used to read them typically can accommodate a limited size fragment of DNA (up to several hundred nucleotides for currently-popular platforms; Jünemann et al. 2013). Because DNA molecules retrieved from ancient remains tend to be much smaller, this library and machine limitation is inconsequential. Second, to amplify library molecules during sequencing – e.g. during bridge amplification or emulsion PCR – a common set of adapters must be ligated onto each molecule. These adapters provide a convenient means to amplify the entire library before sequencing, effectively turning the library itself into a semi-renewable resource (limited by the diversity of DNA fragments present in the sample) (Figure 1). This is an important consideration for libraries derived from rare and precious ancient samples. Third, library construction and sequencing is set up so that the natural ends of each molecule are read from the sequencer. This has enabled observation of the patterns of DNA base damage in ancient DNA molecules at their ends (Gilbert et al. 2006; Briggs et al. 2007), whereas efforts to characterize damage in molecules amplified by primers specific to sequence within them (Pääbo et al. 1989; Briggs et al. 2007; Brotherton et al. 2007) were unable to do so. Finally, the sheer scale of data collection – depending on the machine, up to billions of reads – allows a means to retrieve genome-scale data sets from DNA extracts that are often mostly microbial DNA.

Figure 1.

Library molecules for high-throughput sequencing (HTS) consist of target DNA fragments with adapter sequences ligated on either end. Adapters, with known sequence complementary to primer sequences, allow a single primer pair to amplify a diversity of DNA fragments, and another to be used for the sequencing reaction, where labeled nucleotides are incorporated (Metzker 2010). For ancient DNA studies, HTS technology has allowed researchers to observe damage patterns at ends of molecules and amplify a large variety of genomic DNA fragments of unknown sequence. HTS size limitations are inconsequential, as ancient DNA is usually highly fragmented.

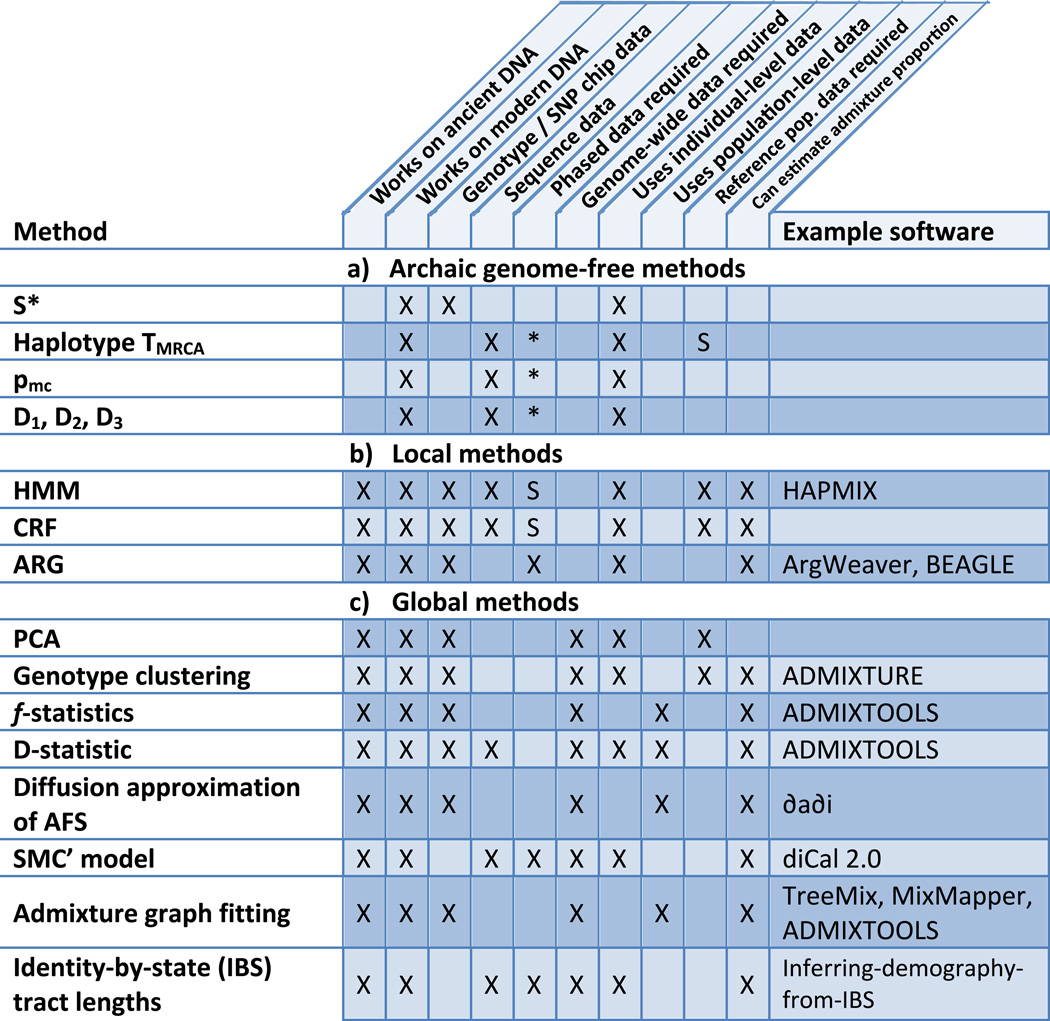
Driven by the accumulation of genome-scale data from ancient remains, a spate of methods for detecting admixture has been recently described. An overview of these methods and their requirements, strengths, and weaknesses is given in Figure 2; they will be described in detail in the following sections. Paleogenomic data and these methods have revealed many surprises in the evolutionary history of numerous species. Perhaps chief amongst these is that hybridization is extensive within the evolutionary history of many vertebrate species, including our own.

Figure 2.

Overview of popular techniques for studying archaic admixture. a: Archaic genome free methods are test statistics that can be used to infer archaic introgression into modern individuals without archaic sequence data. Each is computed on real data, then data simulated under various demographic models, and compared. These are prone to errors in model specification and can produce false positives. b: Local methods can be used to find specific genes or genomic regions admixed individuals derive from one or another ancestral population. These are tuned to detect detect long introgressed haplotypes but have reduced power to detect old admixture events. c: Global methods consider individual sites across the genome. Many are formal tests for admixture and/or can be used to estimate admixture proportion. In each box, “X” means true and “S” means true in some cases. “*” indicates methods applied to haplotype sequences, to which the concept of phasing does not apply. Note that, if sufficiently high-coverage genome-wide sequence data are available, these can be transformed into SNP calls if necessary. Also note that a method working on population-level data requires reference population data by default, as all inputs are population-level.

Detecting admixture without archaic genomes

Before the first paleogenomes had been assembled, approaches to detecting ancient admixture focused on analyzing data from present-day genomes, and in particular human genomes. Part of the reason for this is that single-locus data from ancient hominins, namely Neanderthals, were available for years before the first paleogenomic data that enabled definitive tests for admixture between Neanderthals and humans. By 2006, mitochondrial genomes were available from several Neanderthals, and the genetic divergence between Neanderthal and modern human mitochondrial genomes led to the prevailing view that humans and Neanderthals had not admixed (Serre et al. 2004; Green et al. 2008). Others argued, however, that the data were not incompatible with admixture, for example if gene flow were unidirectional and came only from males, or if enough time had elapsed for genetic drift to remove Neanderthal mitochondrial variants from modern humans (Nordborg 1998; Green et al. 2006). In the absence of a Neanderthal genome sequence, some sought to inform this debate by analyzing patterns within genomes of present-day humans.

Single-locus studies sought to find archaic alleles in present-day humans via a phylogenetic approach. Given sequence data from various human populations, researchers identified haplotypes showing unusually high divergence from other haplotypes, meaning that their time to most recent common ancestor (T_MRCA) is much older than the genome-wide average. Data about geographic distribution of alleles and even archaic sequence data, when available, are incorporated to strengthen findings. This type of approach was used to detect a handful of potentially introgressed haplotypes without ancient sequence data: one specific to present-day Asians, at an X-linked pseudogene called RRM2P4 (Garrigan et al. 2005b), which was later found in the Neanderthal genome (Hammer et al. 2011), as well as other two other haplotypes at clinically significant loci (Hardy et al. 2005; Evans et al. 2006), which were not found in the Neanderthal genome and are thus may have been false positives (Mendez et al. 2012a). More recent single-locus studies have incorporated sequence data from ancient hominins and used similar techniques to discover archaic haplotypes of genes involved in the immune response (Abi-Rached et al. 2011; Mendez et al. 2012a; b).

Plagnol and Wall (Plagnol & Wall 2006) tested for Neanderthal-human admixture using linkage patterns in modern human genomes. They reasoned that if humans had recently (e.g. 40,000 years ago) admixed with an archaic lineage, any introgressed variants should be tightly linked and occur in long (e.g. 40kb) blocks, since recombination would have had insufficient time to further erode the lengths of the archaic haplotypes. They defined a statistic called S*, which seeks to identify sets of SNPs that span long distances and show strong pairwise correlation between genotypes but are not necessarily adjacent, and computed S* over a data set of European and West African individuals. Assessing significance by comparison with simulated data, the authors concluded that European and West African genomes probably both carried genomic segments from separate ancient admixture events (Plagnol & Wall 2006). A follow-up study suggested that the admixture events involved multiple archaic hominin species, and inferred a low level of introgression into East Asians (Wall et al. 2009).

Other investigators have used a variety of techniques to infer archaic admixture from modern sequencing data alone. As in the Plagnol and Wall study, such efforts rely on summary statistics sensitive to admixture. These statistics are used to compare observed data to data simulated under a variety of demographic models, some of which include admixture. S* expanded upon earlier statistics by Wall designed to quantify numbers of tightly correlated genotypes and test demographic models (Wall 2000). Another group developed a summary statistic called p_mc, which identifies basal gene tree clades containing a large proportion of non-African haplotypes, and used it to support the case for the archaic origin of the Asian-specific RRM2P4 haplotype (Cox et al. 2008). Another study that used S* to infer archaic introgression also devised three summary statistics D₁, D₂, and D₃ designed to measure time of admixture, split time between admixing lineages, and extent of admixture, after placing all individuals under study into two groups based on sequence similarity (Hammer et al. 2011). S* has also recently been used to infer archaic admixture in modern African lineages, using whole-genome data (Lachance et al. 2012).

Methods to detect admixture without archaic genomes suffer from several shortcomings that can be avoided by the presence of sequence data from ancient individuals. Many techniques rely, for example, on assumptions about the demographic history of the species under investigation. Demographic model misspecification can thus bias results, as can misspecification of model parameters like mutation and recombination rates. This has led to several cases in which gene haplotypes inferred to have introgressed into modern humans from Neanderthals were not found in the Neanderthal genome (Mendez et al. 2012a). For this reason, ancient sequence data have proven useful.

Detecting admixture with archaic genomes

The availability of sequence data directly from ancient genomes has led many to use as well as develop techniques for inferring admixture from genomic data. Although described here for their utility in ancient DNA studies, these statistical approaches are general-purpose and are used to study admixture in modern organisms as well. They can enable, for example, the inference of ancestry for specific segments of an admixed individual’s genome (local methods), and genome-wide tests for admixture (global methods) that summarize the degree of ancestry components in an admixed individual. Local methods have reduced power to detect old admixture events compared to global methods (Patterson et al. 2012), since they seek to identify long stretches of common ancestry, which recombination will degrade over time. Nonetheless, both categories of methods have developed considerably over the last several years, and both have provided novel insights into species’ evolutionary trajectories.

Local methods

Local methods for ancestry detection are of use to researchers interested in uncovering specific genes or genomic regions that an admixed individual derives from one or another ancestral population. Although they were generally developed without ancient DNA in mind, they have proven useful in recent attempts to investigate specific archaic variants that have been lost or fixed in modern individuals after archaic admixture. They have also been used to reduce noise in data by uncovering variants that individuals have received via gene flow from populations that are not of interest to investigators.

Local methods model an admixed individual’s genome as a series of haplotype blocks, each of which originated in a specific ancestral population. As this requires considering blocks of linked polymorphisms rather than individual SNPs, hidden Markov models (HMMs) are popular local ancestry tools. HMMs are computational models in which sequences of observations are treated as emissions from a set of predefined “states;” in this case, observations are drawn from genotype or sequence data and states correspond to different sources of ancestry. The Viterbi algorithm can then be used to determine the most likely path through states given a sequence of observations (Rabiner 1989; Eddy 2004) and thus assign ancestry to regions of the genome. Early attempts at this strategy were used for admixture mapping in disease studies (Falush et al. 2003; Hoggart et al. 2003, 2004; Patterson et al. 2004; Zhu et al. 2004). Another generation of HMM-based local ancestry methods built upon the same concept but sought to improve parameter estimation by using a more complex model, improving efficiency, or calculating different statistics to use as input observations (Tang et al. 2006; Sundquist et al. 2008; Price et al. 2009; Baran et al. 2012; Brisbin et al. 2012). A popular example, HAPMIX, uses unphased genotype data from admixed individuals to simultaneously determine phase and infer ancestry. Since errors in phasing techniques can cause local ancestry tools to mistake regions of heterozygous ancestry for transitions between ancestral haplotypes, HAPMIX incorporates phasing into the process of inferring ancestry. This is done by representing phase as well as ancestry in the HMM state space and determining the most likely ancestry of each genomic position over all possible phase configurations (Price et al. 2009). In addition to locating introgressed regions, techniques like HAPMIX have been used to find and “mask” regions of European ancestry in Native Americans to improve inference of older population movements (Reich et al. 2012; Raghavan et al. 2015).

Conditional random fields (CRFs) are another, similar tool for local ancestry inference. CRFs can be thought of as generalized hidden Markov models. Where HMMs require each observation in a sequence to be a single data point, CRFs allow each observation to have an arbitrary number of features; this allows a CRF to train on and classify multiple types of data simultaneously (Lafferty et al. 2001). This approach is useful when authors are uncertain which summary statistics will be most useful for inferring ancestry. However, unlike HMMs, CRFs require training data (Rabiner 1989; Lafferty et al. 2001), which usually comes from simulations with known ancestry. A CRF was used in a recent effort to map Neanderthal ancestry in modern human populations (Sankararaman et al. 2014). The features used for ancestry inference had to do with allele sharing patterns, sequence similarity to Neanderthals, and linkage disequilibrium (Sankararaman et al. 2014).

Given current computational resources and available reference data, ancestral recombination graph (ARG) inference may soon become a feasible approach for local ancestry detection (Siepel 2009). The ARG is a representation of all coalescence and recombination events, which join and split lineages going back in time, across all individuals and variable sites in a data set; it is thus a complete description of the relationships between individuals in a population panel, across their genomes (Siepel 2009). ARG inference is computationally challenging, but at least two heuristic implementations currently exist. ArgWeaver (Rasmussen et al. 2014b) constructs the ARG one individual at a time, and uses Markov chain Monte Carlo (MCMC) sampling to draw from the distribution of all possible ARGs when a new individual is added. Song & Hein’s Beagle (Song & Hein 2005), not to be confused with popular haplotype-phasing software of the same name, conceptualizes the ARG as a sequence of trees describing non-recombined haplotype blocks separated by recombination events. Beagle, which was not designed for genome-scale data sets, computes the most parsimonious path between trees along the genome via dynamic programming. An accurate ARG could be used, for example, to determine where in the genome individuals and populations fall in clades with archaic hominins. Current implementations require high-quality, phased genotypes (Song & Hein 2005; Rasmussen et al. 2014b).

Global methods

Global methods for ancestry detection consider individual sites throughout the genome. In this section, we will first describe the most commonly used global methods used to detect ancient admixture in paleogenomic data sets. We will then highlight some of the key discoveries facilitated by these methods. We focus on admixture between humans and archaic hominins, as this is the field in which the majority of the work using these statistics has been performed.

Several global methods arose from other areas of research before large numbers of complete genome sequences were available, and all have limitations. Principal Components Analysis (PCA), in which vectors of genotype data at many loci are projected onto the axes that capture the most variation within them, has a long history and is famous for recapitulating the geographic distribution of humans (Menozzi et al. 1978; Novembre et al. 2008). Despite the visually interpretable results, however, PCA is not a formal test (Patterson et al. 2012) and an individual’s intermediacy between two groups in principal component space does not prove admixture (Yang et al. 2012b). EIGENSTRAT (Price et al. 2006), which relies on PCA to infer ancestry of individuals, thus may wrongly infer admixture in some problematic cases. Structure (Pritchard et al. 2000) and ADMIXTURE (Alexander et al. 2009) are common model-based clustering methods for inferring population structure. These methods attempt to learn local genotype frequencies for a user-defined number of groups across the genome. Then, individuals are described as being mixtures of one or more of these groups. ADMIXTURE provides an estimate of the extent of admixture between groups. Neither of these tests explicitly for significance.

f-statistics

With the advent of paleogenomics came the need for a new set of statistics that could describe tree topologies relating individuals and populations, formally test for admixture, and estimate the percent ancestry that admixed individuals and populations derive from ancestral groups. The f-statistics, which are included in the software package ADMIXTOOLS (Reich et al. 2009; Patterson et al. 2012), are popular for this purpose. The f-statistics work on population-level data, and each describes or tests a phylogenetic relationship by measuring genetic drift conceptualized as variance in allele frequencies along tree branches that is shared between populations. To avoid bias, f-statistics must be computed on sites ascertained in an outgroup to the populations being compared (Patterson et al. 2012).

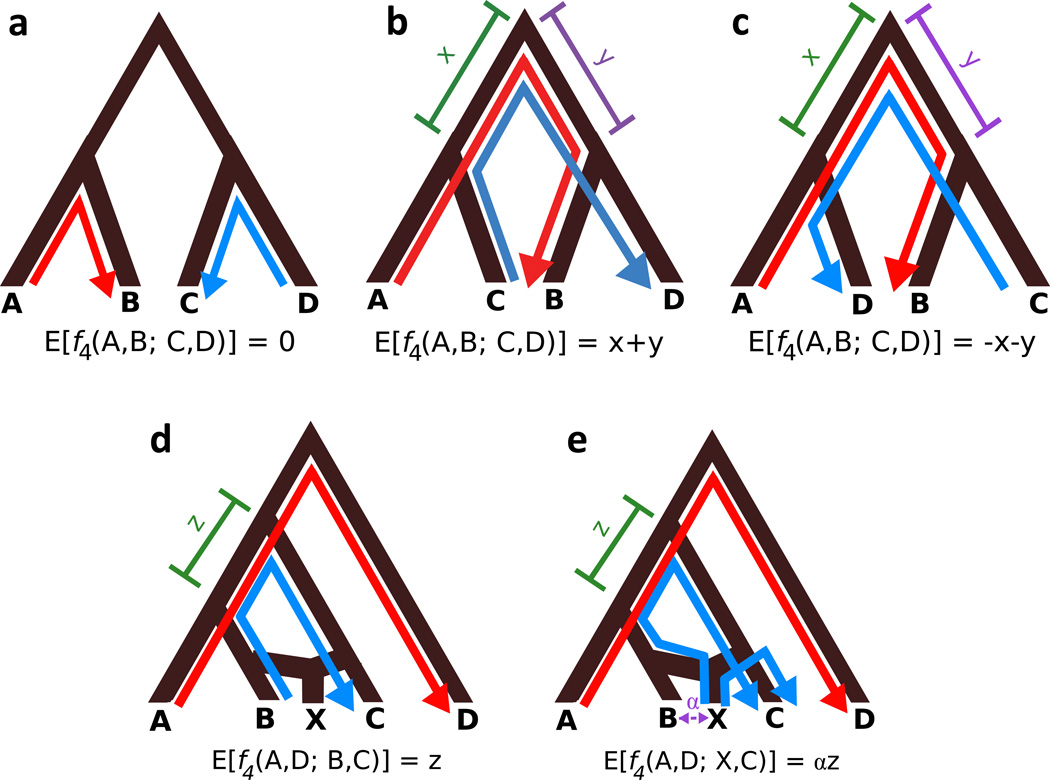
The f₃ statistic is a simple test for whether a population C is a product of admixture between populations A and B. At a single site, f₃(C; A, B) = (c — a)(c — b), where a, b, and c are allele frequencies in populations A, B, and C. When calculated genome-wide, f₃ is usually positive because of genetic drift in the C lineage that is not shared with A or B (Figure 3a, b). When C is the product of admixture between A and B, however, f₃ can be negative (Figure 3 c–f). Negative f₃ is strong evidence for admixture, although a positive f₃ does not necessarily disprove admixture (Reich et al. 2009; Patterson et al. 2012). f₃(C; A, B) can also be used to approximate the relatedness of populations A and B when C is a known outgroup to both (Figure 3 a); this is called an outgroup f₃ statistic (Raghavan et al. 2015).

Figure 3.

Adapted from (Patterson et al. 2012). Expected value of f₃(C; A, B) under various tree topologies. Red lines trace genetic drift between populations C and A; blue lines trace genetic drift between C and B. f₃ measures drift between C and A that is also shared between C and B. Drift is shared along branches where arrows going in the same direction overlap. a and b: expected value of f₃(C; A, B) with no admixture. If C is not a product of admixture between A and B, f₃ is expected to be positive. In the case where C is an outgroup to A and B (a), the value of f₃ is proportional to the distance separating C from A and B, which can also be thought of as the amount of shared history between A and B. c–f: expected value of f₃(C; A, B) when C is a product of admixture between A and B. α is the percent ancestry population C derives from A, and β is the percent derived from B. Distance j represents genetic drift between extant population A its ancestral population that admixed to form the population ancestral to C in the past; distance k is proportional to drift between extant population B and its admixing ancestral population. Computation of f₃(C; A, B) in this case requires tracing multiple paths through the tree, since population C can share drift with population B that it received through admixture with population A and vice versa. The expectation is the sum of all shared drift: E[f₃(C; A, B)] = αβi + α²(i + j) + β²(i + k) + αβ(i — p — q). This has the potential to be negative, although it can also be positive. Given that negative values are impossible if C is not a result of admixture (a and b), a negative result can be taken as evidence of admixture; a positive result, however, cannot be used to reject admixture.

The f₄ statistic is used to estimate the correct phylogenetic relationship between four populations. At a single site, f₄(A, B; C, D) = (a — b)(c — d), where a, b, c, and d are allele frequencies in populations A, B, C, and D. Positive, negative, and zero genome-wide values support different tree topologies (Figure 4 a–c). A technique called f₄ ratio estimation can also be used to estimate the percent ancestry an admixed population derives from an ancestral population (Patterson et al. 2012). If data exist from admixing populations B and C, admixed population X, population A (which is more closely related to B than C), and outgroup population D, f₄ ratio estimation can approximate the percent ancestry α that X derives from B. The estimate for α is given by f₄(A, D; X, C)/f₄(A, D; B, C) (Figure 4d, e) (Patterson et al. 2012).

Figure 4.

Adapted from (Reich et al. 2009). Visual explanation of expected values of f₄(A, B; C, D) under various tree topologies. Red lines trace genetic drift from A to B; blue lines trace drift from C to D. f₄ measures drift shared between A and B that is also shared between C and D. Drift is shared along branches where arrows overlap going in the same direction. a–c: Positive, negative, and zero values of f₄ give support for different tree topologies relating the four populations. d, e: visual explanation of f₄ ratio method for inferring admixture proportion. Population X is a mixture of populations related to B and C; population D is an outgroup. The quantity of interest, α, is the proportion of ancestry population X has received from B. If the expected value of f₄(A, D; B, C) = z (d), then the expected value of f₄(A, D; X, C) = αz (e). It follows that α = f₄(A, D; B, C)/f₄(A, D; X, C) (Patterson et al. 2012).

Haak et al (Haak et al. 2015) used the f₄ statistic in a more exploratory way, to identify populations that may have contributed DNA to an admixed population of interest, and to estimate the amount of ancestry contributed by each of the admixing populations. The authors defined a set of candidate admixing populations Ref₁, Ref₂, … Ref_N that may have contributed ancestry to the population of interest Test in unknown proportions α₁, α₂, … α_N. They then chose three outgroup populations A, B, and C, none of which share recent gene flow with Test or Ref₁…Ref_N. They observed that $f_4(\mathit{\text{Test}},\mathrm{A};\mathrm{B},\mathrm{C})={\sum }_{i=1}^N{\alpha }_i{f}_4({\mathit{\text{Ref}}}_i,\mathrm{A};\mathrm{B},\mathrm{C})$. After calculating f₄ for each candidate reference population and every possible permutation of available outgroups, the authors were able to calculate the α_i admixture coefficients for each candidate admixing population via linear regression (Haak et al. 2015).

D-statistic

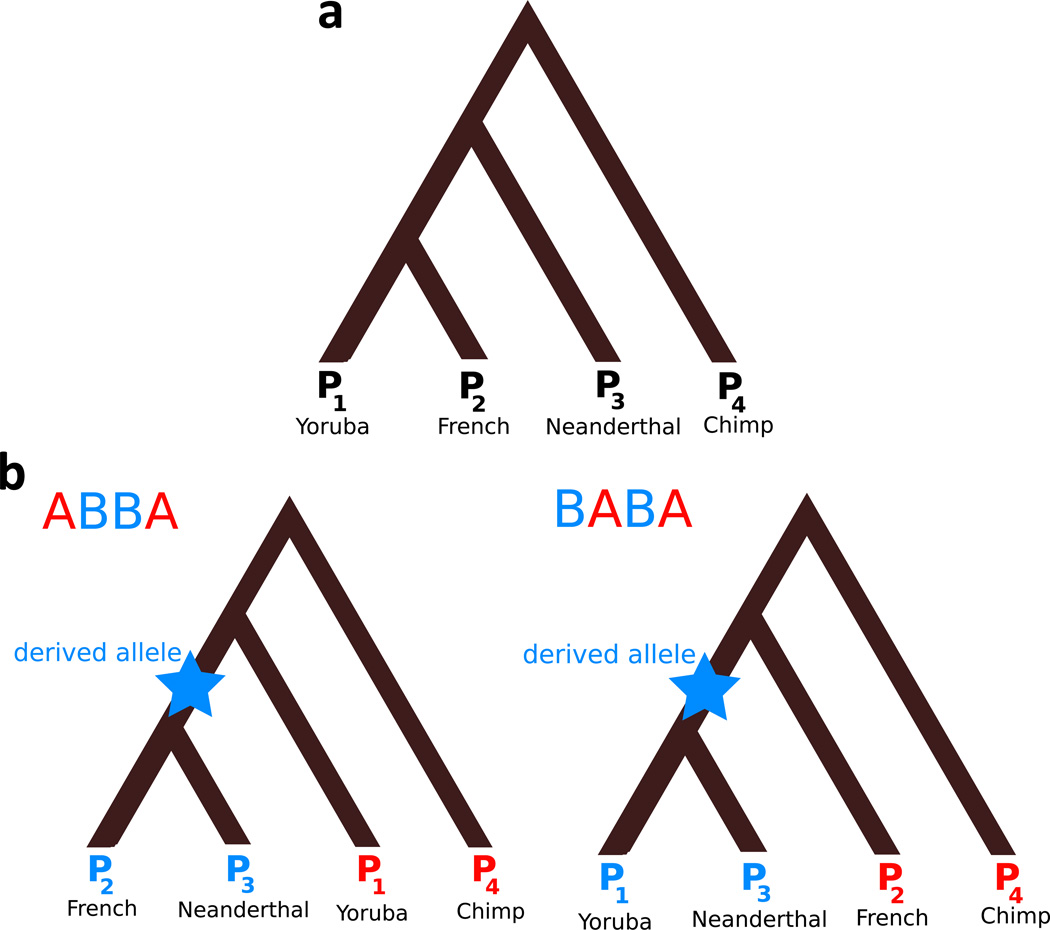
Another popular genome-wide test for admixture is the D-statistic (Green et al. 2010; Durand et al. 2011). D can be computed using either individual genomes or population allele frequency data (Durand et al. 2011). In the case of individual genomes, D requires sequence from two potentially admixed individuals, P₁ and P₂, a candidate admixing individual, P₃, and an outgroup P₄. D always falls between −1 and 1; it is positive if P₁ shares more derived alleles with P₃ than P₂ shares with P₃. D is negative if P₂ shares more derived alleles with to P₃ than P1 shares with P₃. The idea behind D is that, if there has been gene flow from the population of which P₃ is a member, then any admixed individual (P₁ or P₂) will share more derived alleles with P₃ than an unadmixed individual. To calculate D, one scans the genome for sites where P₂ shares a derived allele with a P₃, termed ABBA sites. To compensate for incomplete lineage sorting (ILS), this is subtracted from this the number of sites at which P₁ shares a derived allele with P₃, termed BABA sites. Then $\mathrm{D}=\frac{N_{\mathit{\text{ABBA}}}-N_{\mathit{\text{BABA}}}}{N_{\mathit{\text{ABBA}}}+N_{\mathit{\text{BABA}}}}$, where N_ABBA is the total number of ABBA sites and N_BABA is the number of BABA sites (Figure 5) (Green et al. 2010). Random processes like ILS and recurrent mutation can produce ABBA and BABA sites, but should produce an equal number of both. Admixture, if it occurs, will only increase ABBA or BABA counts in the admixed individual. D is robust to fluctuating ancestral population sizes but can be confounded by ancestral population structure (Durand et al. 2011). One recent study, seeking to minimize the noise resulting from ancestral population structure, restricted D to sites where individuals from a population believed to be free of admixture matched the outgroup P₄ and thus carried the ancestral allele. This technique is called an “enhanced D-statistic” and can improve power to detect admixture, but it can also introduce bias. If analysis is restricted to sites where individuals from unadmixed population P₀ match the outgroup P₄, and populations P₁ and P₂ are equally related to P₃ but not equally related to P₀, D_enhanced(P₁, P₂, P₃, P₄) can deviate from zero, although the expectation of D(P₁, P₂, P₃, P₄) is zero (Meyer et al. 2012).

Figure 5.

Explanation of D statistic (Green et al. 2010; Durand et al. 2011). Individuals are numbered according to the D-statistic notation: D(P₁, P₂, P₃, P₄) and examples of individuals that could be used to yield a positive D-statistic result when testing for Neanderthal ancestry are given (D would be negative in this case if there had been gene flow between the Yoruban and Neanderthal instead). a: genome-wide tree relating the four individuals, based on prior knowledge. b: trees at ABBA and BABA sites used to compute D. In both, blue is used to represent a derived allele (does not match chimpanzee); red represents an ancestral allele (matches chimpanzee). To calculate D on sequence data, the number of sites with the topology of the left tree is N_ABBA and the number of sites with the topology of the right tree is N_BABA. Then $\mathrm{D}=\frac{N_{\mathit{\text{ABBA}}}-N_{\mathit{\text{BABA}}}}{N_{\mathit{\text{ABBA}}}+N_{\mathit{\text{BABA}}}}$.

D can be used in other ways as well. Like the f statistics, D can be calculated on population genotype data by replacing N_ABBA and N_BABA with products of allele frequencies in the four populations (Durand et al. 2011). Another statistic f̂ (Green et al. 2010; Durand et al. 2011) uses D to estimate admixture proportion: if P_3a and P_3b are two individuals from population P₃, then $\widehat{f}=\frac{\mathrm{D}({\mathrm{P}}_1,{\mathrm{P}}_2,{\mathrm{P}}_3,{\mathrm{P}}_4)}{\mathrm{D}({\mathrm{P}}_1,{\mathrm{P}}_{3\mathrm{a}},{\mathrm{P}}_{3\mathrm{b}},{\mathrm{P}}_4)}$, and it can be understood as a ratio of D calculated on the admixed individual to D calculated on an individual from the admixing population. D can also be calculated without a candidate admixing individual P₃, if a different outgroup P₀ to P₁ and P₂ is available: E[D(P₂, P₁, P₀, P₄)] ∝ E[D(P₁, P₂, P₃, P₄)], with the value changing slightly due to this statistic’s dependence on the split time of P₀ and the P₁/P₂ lineage, rather than the time of admixture (Durand et al. 2011). Finally, Eaton and Ree introduced a variation on the D statistic, which they call the partitioned D statistic (Eaton & Ree 2013) and used it to analyze RADseq data collected from a genus of flowering plants within the broomrape family. This method is designed to remove the effect of shared ancestry amongst multiple candidate admixing populations by quantifying the number of derived alleles that are common in both and found in the admixed population.

Weighted block jackknife

A weighted block jackknife approach (Künsch 1989) can be used to assess significance of f and D statistics. To overcome bias introduced by linkage disequilibrium (LD), the block jackknife technique divides the genome into M blocks, each of which must be long enough to overcome LD between adjacent blocks. Appropriate block size can be determined by performing the block jackknife repeatedly with increasing block sizes until standard error estimates converge (Reich et al. 2009; Green et al. 2010). Each block is then removed from the genome in turn, and the test statistic is computed over the rest of the genome. In the case of D, a single jackknife computation is D_i for i = 1, 2, … M, the mean ${\mathrm{D}}_{\mu }=\frac{1}{M}{\sum }_{i=1}^M{D}_i$, and the weight of jackknife block i is $W_i=\frac{N_i}{{\sum }_{j=1}^M{N}_j}$ where N_i is the number of informative sites in the block and ${\sum }_{j=1}^M{N}_j$ is the number of informative sites in the genome. The weighted variance of D in an individual is then given by ${\sum }_{i=1}^M{W}_i{({\mathrm{D}}_i-{\mathrm{D}}_{\mu })}^2$ and standard error is $S{E}_{\mathrm{D}}=\sqrt{M{\sum }_{i=1}^M{W}_i{({\mathrm{D}}_i-{\mathrm{D}}_{\mu })}^2}$ (Green et al 2010). Since the expectation of D is zero, Z scores can then be computed from D scores as Z = D/SE_D.

Other approaches

Other approaches to detecting archaic admixture use information about specific demographic and evolutionary parameters, such as split times between populations, population structure, and natural selection. The program ∂a∂i (Gutenkunst et al. 2009) considers the derived allele frequency in multiple populations at sites throughout the genome, termed the multi-population allele frequency spectrum (AFS). The expected AFS under a model that can include selection and migration is computed by solving a diffusion equation that approximates AFS evolution over time. Model parameters including extent of migration are then adjusted via (composite) maximum likelihood estimation to fit the observed AFS (Gutenkunst et al. 2009). diCal 2.0 builds on the theory of the sequentially Markov conditional sampling distribution (Paul & Song 2010), using a hidden Markov model that trains on observed haplotypes and has states corresponding to discretized time points in the past. This HMM can be used to estimate parameters for demographic models that include population structure and migration (Steinrücken et al. 2013). TreeMix (Pickrell & Pritchard 2012), MixMapper (Lipson et al. 2013), and qpGraph from ADMIXTOOLS (Patterson et al. 2012) all build on the concept of fitting graphs rather than trees to genotype data, allowing for migration between nodes.

Another set of methods seek to infer demographic parameters like admixture extent from linkage disequilibrium patterns (Pool & Nielsen 2008; Patterson et al. 2012; Harris & Nielsen 2013). In a popular implementation of this approach, pairs of phased haplotypes are drawn from populations of interest, and the distribution of lengths of identity state (IBS) tracts, or runs of identical sequence flanked by variable sites, is computed (Harris & Nielsen 2013). This distribution is then compared to one expected under a demographic model and used to optimize model parameters, which can include population growth rates, divergence times, and rates of admixture (Harris & Nielsen 2013).

Detecting admixture with archaic hominins

One of the most visible contributions of paleogenomic studies to current understanding of admixture is the detection of gene flow between archaic hominins and modern humans. The first direct genetic evidence of admixture between Neanderthals and anatomically modern humans was from the 2010 publication of a draft Neanderthal genome sequence (Green et al. 2010), which expanded upon an earlier analysis of 1 megabase of the Neanderthal genome that hinted at possible Neanderthal-human admixture (Green et al. 2006). Using the D-statistic and sequences from modern humans, Green et al. inferred Neanderthal gene flow into all non-Africans, and estimated the Neanderthal proportion of non-Africans’ ancestry to be 1–4% (Green et al. 2010). A subsequent study using a higher-quality Neanderthal genome revised this to 1.5–2.1% and concluded that the Neanderthal that admixed with modern Eurasians was more closely related to a Neanderthal from the Caucasus than to Neanderthals from the Altai Mountains and Croatia, suggesting a possible location for admixture (Prüfer et al. 2014).

Although the D-statistic can be confounded by ancestral population structure (Durand et al. 2011), and some studies have suggested that such structure did exist in early humans (Garrigan et al. 2005a), other lines of evidence support Neanderthal-human admixture. First, patterns of linkage disequilibrium (LD) in present-day humans suggest admixture occurred 47–65 kya, more recently than would be expected if Neanderthal-like haplotypes were the result of ancestral population structure (Sankararaman et al. 2012). Second, a comparison of the site frequency spectrum of real data with that simulated under models of ancestral population structure and recent admixture also supported the recent admixture scenario (Yang et al. 2012a). The most convincing evidence came, however, from a more recent analysis of a previously unknown archaic hominin called the Denisovan. Denisovan DNA was extracted from a 30–50,000 year old finger bone found in Denisova cave in southern Siberia and was found to belong to a previously undiscovered hominin lineage (Krause et al. 2010; Reich et al. 2010). Phylogenies inferred from Denisovan mitochondrial and nuclear DNA are discordant: mitochondrial DNA suggests a deep, ~1 mya divergence between the Denisovan lineage and a clade containing both human and Neanderthal lineages (Krause et al. 2010), while nuclear loci place the Denisovan closer to Neanderthals (~650 kya diverged) than to modern humans (~800 kya diverged) (Reich et al. 2010). This discordance suggests either incomplete lineage sorting in a small population descended from a much larger one or admixture with an as-yet unknown archaic hominin with a more ancient divergence from humans and Neanderthals (Reich et al. 2010). A subsequent study that included demographic simulations supported the admixture hypothesis, while also detecting a small amount of gene flow from Neanderthals into the Denisovan (Prüfer et al. 2014).

Like Neanderthals, the Denisovan appears to have contributed to the modern human gene pool. Using the D-statistic, about 3–6% of the genomes of present-day Australian aborigines and Melanesians are of Denisovan-like origin (Reich et al. 2010; Meyer et al. 2012), as opposed to 0.2% of East Asian and Native American genomes and little to none of the genomes of other groups (Prüfer et al. 2014). A possible explanation for this pattern is admixture with the ancestors of Australians and Melanesians followed by migration of admixed Oceanians to East Asia (Prüfer et al. 2014). Another study suggests that New Guineans were the source for Denisovan ancestry detected in all other groups, including Australian aborigines (Qin & Stoneking 2015).

This discovery that Denisovans admixed with modern humans has had two consequences. First, it bolsters the case for Neanderthal-human admixture. If the signal of Neanderthal-human admixture resulted from structure in the ancestral African population, then the Denisovan should exhibit excess allele sharing with all non-Africans and not just Australians and Melanesians, because of the phylogenetic proximity of the Denisovan to Neanderthals (Meyer et al. 2012). Second, it creates a geographic mystery. Although the range of the Denisovan population is not known, it is unclear how a Siberian population could have admixed with the ancestors of Australians and Melanesians. This mystery is compounded by the recent discovery of a ~400,000 year old hominin bone from Sima de los Huesos in Spain, which has Neanderthallike morphological features and mitochondrial DNA that is very similar to the Denisovan (Meyer et al. 2014). Given that the Denisovan mitochondrial haplotype may have originated within another, unknown hominin lineage (Reich et al. 2010; Prüfer et al. 2014), this creates a connection between hominin lineages in western Europe, southern Siberia, and Oceania that is yet to be fully understood (Meyer et al. 2014).

Ancient remains of modern humans have also helped inform the study of Neanderthal-human admixture. In 2014, the genome of a 45,000 year old human male from the Ust’Ishim site in Siberia was sequenced (Fu et al. 2014). Computational analysis, which included D-statistics to detect gene flow and f₄ ratio estimation to quantify that gene flow, determined that the individual came from a population ancestral to both modern Europeans and Asians, and had tracts of Neanderthal ancestry that were longer than those found in modern humans (Fu et al. 2014). The length distribution of Neanderthal haplotypes was used to estimate that the Ust’Ishim individual’s Neanderthal ancestor lived between 50 and 60 kya (Fu et al. 2014). In addition to Ust’Ishim, two other ancient human genomes were found to have longer tracts of Neanderthal ancestry than modern humans: a 36–39,000 year old individual from western Russia (Seguin-Orlando et al. 2014), and a 37–42,000 year old human from Peştera cu Oase in Romania (Fu et al. 2015). In an analysis similar to the Ust’Ishim study (Fu et al. 2014), the latter was found to have a substantially larger Neanderthal component than present-day humans, with longer un-recombined Neanderthal haplotype blocks (Fu et al. 2015). Fu et al. concluded that the Peştera cu Oase individual was only 4–6 generations removed from a Neanderthal ancestor and may have had one or more other Neanderthal ancestors. This finding weakens the case for a single human-Neanderthal admixture event and suggests that at least one admixture event may have taken place in Europe.

The idea of multiple admixture events has been upheld by computational studies. Contrary to initial reports, recent studies have detected more Neanderthal ancestry in East Asians compared to Europeans (Wall et al. 2013; Sankararaman et al. 2014; Vernot & Akey 2014). One proposed explanation for this is that Neanderthal alleles are generally deleterious and thus were able to drift to higher frequency in the historically smaller East Asian population than in the historically larger European population, where purifying selection would have been more powerful (Sankararaman et al. 2014). Another explanation is a “two-pulse” model of admixture, in which the ancestors of East Asians admix with Neanderthals a second time, after the population split from western Eurasians (Vernot & Akey 2014). Simulations under different demographic models have upheld either the latter scenario or a more complex scenario involving admixture with other groups, as more likely than the former (Kim & Lohmueller 2015; Vernot & Akey 2015). These studies are leading to a new view of hominin history in which barriers between divergent taxa are porous and rapid adaptation to new environments may have been facilitated in part by gene flow (Pääbo 2015).

Many studies have moved beyond population genetics and sought to identify selective consequences of Neanderthal and Denisovan alleles present in modern humans. In some cases, there appears to have been adaptive introgression, as with several non-African human leukocyte antigen (HLA) haplotypes that may have originated in Neanderthals and Denisovans, where they probably arose under selective pressure from local pathogens long before modern humans migrated to the same areas (Abi-Rached et al. 2011). In other cases, deleterious alleles introgressed from an archaic hominin and then went to high frequency in modern human populations, as with a set of disease-related variants discovered by a whole-genome scan (Sankararaman et al. 2014) and a Neanderthal-origin haplotype across the gene SLC16A11 that poses high diabetes risk (Williams et al. 2014). The diabetes risk allele could, however, have originally conferred a selective advantage to ancient humans upon entering a new habitat and adopting a new diet (Racimo et al. 2015). Other studies, reviewed in Racimo et al (2015), have discovered cases in which selection has apparently spread archaic alleles of genes involved in immune defense, altitude adaptation, skin and hair phenotypes, and lipid metabolism. In addition to uncovering many cases of adaptive introgression, two recent studies that mapped out Neanderthal ancestry in present-day humans found depletion of Neanderthal sequence in and around coding regions, suggesting that natural selection may have acted to eliminate many Neanderthal variants (Sankararaman et al. 2014; Vernot & Akey 2014).

Inferring modern human migrations

Beyond Neanderthals and Denisovans, ancient DNA and statistics for detecting admixture can be used to infer the movement of genes, and therefore people, between locations. In addition to D and f-statistics, approaches to infer patterns of migration and admixture include but are not limited to admixture graph fitting, demographic model fitting to the sequentially Markovian conditional sampling distribution (diCal 2.0), and characterization of identity by state (IBS) tract length distributions. Together, these statistical approaches have reframed the existing view about the timing and nature of human movements across the globe.

In reconstructing the history of the peopling of Europe, for example, two early observations from paleogenomes demanded a context. First, the genome of Ötzi, a 5,300 year old man from the Italian alps, was found to resemble the genomes of present-day Sardinians (Keller et al. 2012). Second, the genome of a 24,000 year old boy from Mal’ta in south-central Siberia was found to share ancestry with both present-day European and Native American genomes (Raghavan et al. 2014b). A larger study followed up on these findings, adding many present-day genomes as well as several from ancient European farmers and hunter gatherers (Lazaridis et al. 2014). This study inferred that modern Europeans descend from three genetic sources: western European hunter-gatherers, early farmers from the Middle East, and a mystery population related to ancient Siberians and Native Americans (Lazaridis et al. 2014). This study also showed that Ötzi’s affinity to modern-day Sardinians was a trait shared with other Neolithic farmers (Lazaridis et al. 2014). Two more recent studies, one with 69 (Haak et al. 2015) and another with 101 ancient genomes (Allentoft et al. 2015), provided greater detail about past human migrations. In particular, these studies suggested that the mystery population identified earlier was probably a mixture of Eastern European hunter-gatherers, which were related to the ancient Siberian samples and Native Americans and to herders from the Eurasian steppe. This population was estimated to have invaded Europe during the Late Neolithic, after which they contributed genes to all populations, were a source for wheeled cart technology and Indo-European languages, and led to the rise of the Corded Ware culture throughout Copper Age Europe (Allentoft et al. 2015; Haak et al. 2015). This same group, known as Yamnaya, also spread east to create the Andronovo culture in the Altai region in Siberia, which later changed as it received migrants from East Asia in the Iron Age (Allentoft et al. 2015).

Admixture-based analyses of ancient human genomes have also shed light on the ongoing debate about the peopling of the Americas, in particular about whether Native Americans are descendants of a single group that migrated across the Bering Strait in the Late Pleistocene or a more complex mixture of groups. To date, Native American paleogenomes have shown strong continuity with present-day Native Americans, challenging hypotheses about ancient admixture that were based on analyses of skelet al morphology (Rasmussen et al. 2014a, 2015). One recent study divided Native Americans into three lineages: “First Americans,” Eskimo-Aleut speakers, and Na Dene speakers, and concluded that each of these could have represented a separate migration from Asia, with subsequent admixture and some possible back-migration from First Americans to Asia (Reich et al. 2012). In contrast, a subsequent larger study concluded that “First Americans” and Na Dene speakers more likely diverged within the Americas, while the Inuit may represent a separate migration (Raghavan et al. 2015).

Several studies have also attempted to address the possible gene flow from Oceanians into Native American populations, which was first detected by the observation of low levels of Denisovan DNA in the New World (Prüfer et al. 2014; Qin & Stoneking 2015). One study found a weak signal of differential Oceanian ancestry in New World populations, and concluded that a small amount of Oceanian ancestry made its way to different parts of the Americas via admixture first with East Asians and later with Aleutian Islanders (Raghavan et al. 2015). Another detects Oceanian admixture in several Amazonian groups and argues for a larger Melanesian presence among New World populations (Skoglund et al. 2015).

One feature that distinguishes several of these recent ancient DNA investigations of human migration and demography from past ones is an increase in both the number of samples and the variety of analysis techniques used. In contrast to previous studies in which one or several paleogenomes were analyzed, e.g. (Reich et al. 2010; Green et al. 2010; Prüfer et al. 2014), several recent studies have used dozens of samples (Raghavan et al. 2014a, 2015; Allentoft et al. 2015; Haak et al. 2015; Skoglund et al. 2015).

Owing to the lack of well-preserved hominin remains, some global regions, like Africa, have thus far been difficult to study using ancient DNA (Shapiro & Hofreiter 2014). Using patterns of Neanderthal ancestry, however, researchers have detected possible back-migrations from Eurasia to eastern Africa (Abi-Rached et al. 2011; Prüfer et al. 2014). More recently, ancient human remains with high endogenous DNA content were discovered in Ethiopia and yielded the first ancient African genome, called Mota (Llorente et al. 2015). Furthermore, several groups have sought to expand upon the original discovery of possible archaic introgression into African groups based on S* (Plagnol & Wall 2006; Wall et al. 2009). For example, one study of noncoding autosomal loci inferred archaic gene flow into a variety of central and southern African populations within the last 70,000 years, to the exclusion of a West African agriculturalist population (Hammer et al. 2011). Another group calculated S* across genomes of African hunter-gatherer populations and concluded that there had been multiple instances of archaic introgression, first into the common ancestors of this group and later as regional admixture events (Lachance et al. 2012). Follow-up studies will be needed to assess whether this signal might be the result of ancestral population structure rather than admixture.

Detecting ancient admixture in other species

Although hominins remain the most popular lineage for ancient admixture studies, advances have also been made in understanding the history of gene flow in other species. Within mammals, a recent study investigating the relationship between modern cattle and aurochs, their extinct wild ancestor, used the D-statistic to detect a low level of gene flow from aurochs into British and Irish cattle breeds in the period since domestication (Park et al. 2015). While lacking nuclear sequence data, another study using ancient DNA from mammoths analyzed mitochondrial genomes from the morphologically divergent Columbian mammoth and wooly mammoth species. The authors found that the Columbian mammoth’s mtDNA fell within the diversity of that of the wooly mammoth, and thus that the two species may have hybridized at some point in time; this suggests a follow-up study involving nuclear data (Enk et al. 2011).

Admixture studies using ancient DNA have been applied to plants and fungi as well. A group interested in maize, specifically its arrival in and adaptation to the US Southwest about 4,000 years ago, sought to settle a debate about its route of diffusion using ancient DNA. By sequencing 32 ancient maize samples spanning much of the history of maize domestication and geographic spread, the authors found, using the D-statistic, TreeMix, and a genotype clustering method, that maize in the US Southwest likely spread from highland Mexico, with subsequent gene flow from coastal varieties (da Fonseca et al. 2015). Another study sought to clarify interspecific relationships and centers of origin within the fungal genus Phytophthora, which includes the pathogen responsible for late blight, the cause of the Irish potato famine. They found, using the same methods, that P. andina, a species native to the Andes, appears to have arisen through hybridization between a species closely related to that which caused the potato famine, and an as-yet unknown outgroup to the other species examined (Martin et al. 2015).

It is worth noting that high-coverage ancient genomes from non-hominin species are just now becoming available (e.g. Lynch et al. 2015; Palkopoulou et al. 2015). Just as studies of archaic hominin admixture have been enabled by the growing diversity of genomic data from humans and their close relatives, future progress in other taxa should enable detection and characterization of ancient admixture events in lineages further removed from our own. These studies will no doubt provide important insights into the effects of hybridization and gene flow on speciation and environmental adaptation (Abbott et al. 2013).

Conclusion

Recent advances in extraction, sequencing, and analysis of ancient DNA have led the field away from studies of single loci and into the field of paleogenomics, where more ambitious studies and detection of admixture and inter-population migration are now possible. Such studies have both co-opted existing techniques and mandated the development of new tools for detecting and quantifying admixture. With these, they have shed light on past admixture events, in both the recent and distant past, that have changed our understanding of who we are as a species. As reference data become more available, and ancient DNA studies become more ambitious in sequencing a larger portion of genomes of an expanding number of ancient taxa, innovative new computational analysis techniques will follow. The result will be a wider perspective on the complex web of interactions between species past and present that defines Earth’s recent biological history.