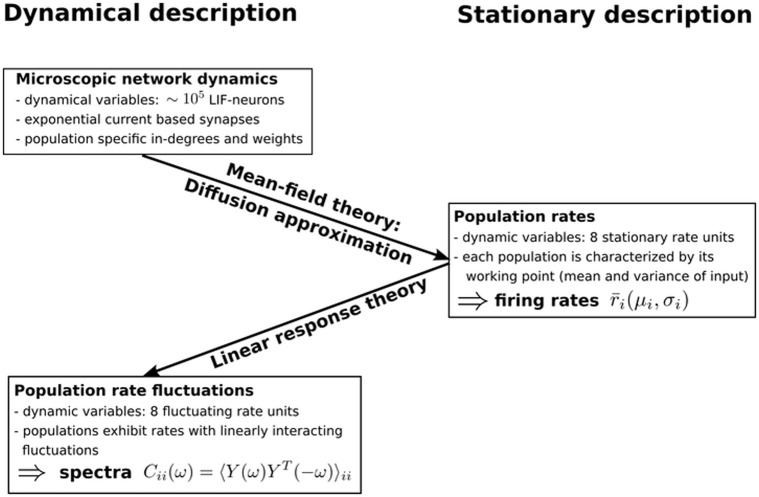
Fig 2. Sketch of the mean-field reduction and linear response theory of fluctuations.

Graphical representation of the two-step reduction carried out when deriving the description of fluctuations in recurrent networks. First, the working point of each population, determined by the mean and variance of its input is established by means of diffusion approximation. The working point suffices to predict the stationary firing rates of the populations, which follow from the self-consistent solution of a set of mean-field equations. This step constitutes a dimensionality reduction from two dynamic variables for each of the N = 77169 neurons, to one dynamic variable for each of the eight populations. Second, the dynamical responses of the populations are approximated by linear response theory around the stationary solution. The fluctuations of the population activities can subsequently be mapped to a linear rate model. The derived description of the rate fluctuations yields the population rate spectra, as described in “Fluctuation dynamics”.