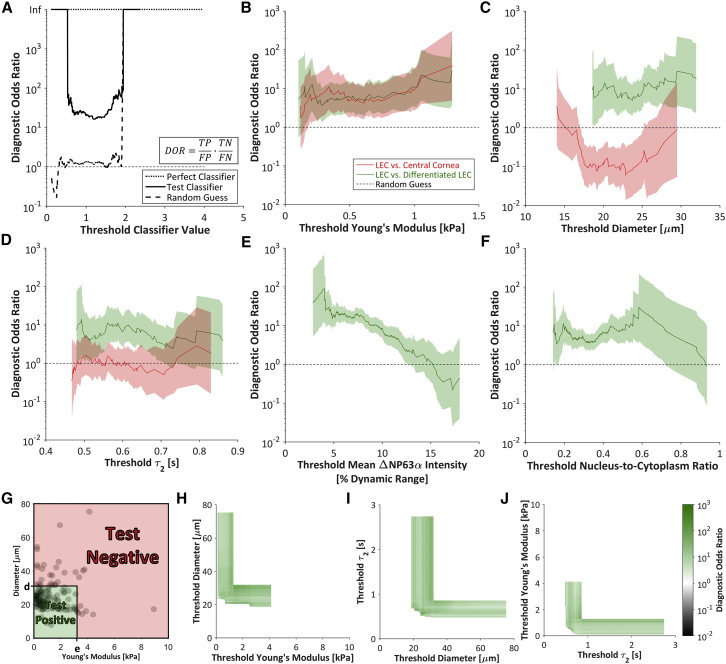
Figure 7.

DOR. (A) The DOR measures the overall utility of a binary classifier by $TP\cdot TN/FP\cdot FN$. The DOR of a perfect classifier (dotted line) is infinite for any threshold value, whereas the DOR of a random classifier (dashed line) is ∼1, and a test classifier (solid line) will have a finite DOR of >1. Extreme threshold classifier values yield an infinite DOR (where FP = 0 or FN = 0). (B–F) The DORs based on the (B) Young’s modulus, (C) diameter, (D) slow viscoelastic time constant, (E) mean ΔNP63α intensity, and (F) nucleus/cytoplasm ratio were generally higher for the selection of LECs against differentiated LECs than against central cornea cells. The DOR based on the Young’s modulus was ∼10 regardless of the threshold value. Shaded regions indicate 95% CI. (G) To determine the utility of a two-parameter classifier, cells below both the diameter threshold, d, and the Young’s modulus threshold, e, were defined as test positive. All other cells were defined as test negative. (H–J) For all possible combinations of (H) threshold diameter and threshold Young’s modulus, (I) threshold slow viscoelastic time constant (τ₂) and threshold diameter, and (J) threshold Young’s modulus and threshold slow viscoelastic time constant, the DOR was calculated for selection of LECs against differentiated LECs. The increase in DOR upon inclusion of a second classifier indicates that the combined classifiers can outperform the single-parameter classifiers. The DORs ranged from 0.01 to 1000. To see this figure in color, go online.