Applied Concepts in PBPK Modeling: How to Build a PBPK/PD Model

Abstract

The aim of this tutorial is to introduce the fundamental concepts of physiologically based pharmacokinetic/pharmacodynamic (PBPK/PD) modeling with a special focus on their practical implementation in a typical PBPK model building workflow. To illustrate basic steps in PBPK model building, a PBPK model for ciprofloxacin will be constructed and coupled to a pharmacodynamic model to simulate the antibacterial activity of ciprofloxacin treatment.

GENERAL INTRODUCTION TO PBPK MODELING

Overview of PBPK

In recent decades, different types of computational models have been applied in drug development programs. PBPK models combine information on the drug with independent prior knowledge on the physiology and biology at the organism level to achieve a mechanistic representation of the drug in biological systems, allowing the a priori simulation of drug concentration–time profiles. Since PBPK models explicitly consider different organs and tissues, it is possible to obtain the quantitative characterization of concentration–time profiles in the respective compartments. Such prediction is of high pharmacological relevance since it enables the estimation of drug exposure not only in plasma but also at the site of action, which may be difficult or impossible to measure experimentally.

A whole‐body PBPK model (Figure 1 a) contains an explicit representation of the organs that are most relevant to the absorption, distribution, excretion, and metabolization of the drug due to their physiological/pharmacological function or their volume.1 These are typically heart, lung, brain, stomach, spleen, pancreas, gut, liver, kidney, gonads, thymus, adipose tissue, muscle, bone, and skin. The tissues are linked by the arterial and venous blood compartments, and each one of them is characterized by an associated blood‐flow rate, volume, tissue‐partition coefficient, and permeability. A major advantage of PBPK modeling is the availability of a comprehensive structural representation of the physiology of an organism. The various parameters in the model are either obtained from compilations of prior knowledge or may be calculated from specific and carefully validated formulas. From a general point of view, it is possible to distinguish between organism parameters on the one hand and drug parameters on the other.

Figure 1.

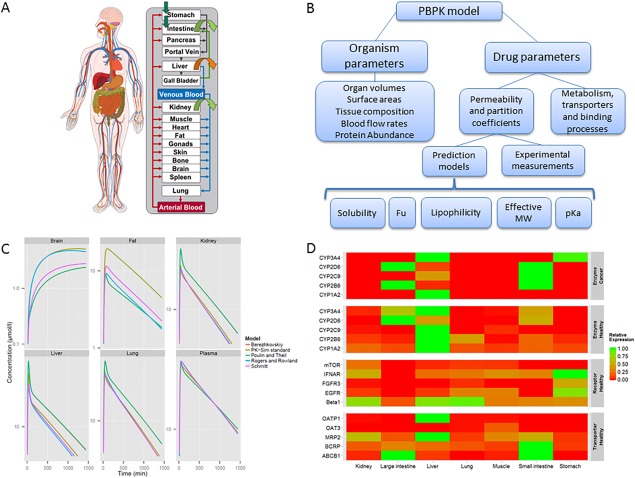
(a) Representation of the generic structure of a whole‐body PBPK model. (b) Hierarchical representation of the main physiological and drug parameters in a PBPK model. (c) Simulation of drug concentrations in different tissues using different distribution models for theophylline. This illustrates the impact of the choice of the distribution model on the simulated tissue concentration profiles even though corresponding plasma concentrations are very similar. (d) Example of relative gene expression data for a group of enzymes (in healthy and cancer patients), receptors, and transporters. Gene expression is represented as relative value obtained through normalization to the tissue or organ with the highest expression.

Figure 1 b represents the hierarchical relationship of the most important parameters in a PBPK model. The organism parameters are usually used as direct input in the model, representing the knowledge available a priori on the anatomy and physiology. When dedicated software packages are used, such information is usually contained in the database of the PBPK software available. By contrast, the drug parameters in the model are related to the compound partition coefficient and permeability across biological membranes. In some cases such parameters can be measured in vivo or in vitro, but most often they are estimated from the physicochemical properties of the drug. In this context, physicochemical parameters act as surrogate parameters for the calculation of the compound distribution. For this reason they can, in some cases, differ from the corresponding measured value. This is particularly evident in the case of lipophilicity, since this parameter is usually measured under experimental in vitro conditions (e.g., octanol‐water partitioning) which do not match in vivo conditions in the biological environment. Usually the calculation of membrane permeabilities or partition coefficients is automatically performed by the PBPK software. The latter parameters are estimated from so‐called distribution models quantifying equilibrium between plasma and the surrounding tissue. As an example, in Figure 1 c the tissue and plasma concentrations of theophylline estimated from its physicochemical properties using different distribution models are illustrated. As can be seen, the different models simulate different concentrations in the different organs; this point will be discussed in more detail in the section “Distribution models” (below).

While passive processes can be calculated from such model‐based relationships, there is currently no similar method for a priori prediction of the kinetics of active processes (e.g., metabolism, target binding, or active transport of the drug). One way to quantify the contribution of different organs to total clearance at the whole‐body level is use of in vitro–in vivo extrapolation.2 Furthermore, the relative tissue‐specific expression of genes or proteins might be considered.3 An example of gene expression data is shown in Figure 1 d, where the relative expression normalized to the tissue with the highest expression is represented for a group of enzymes, in healthy individuals and cancer patients, respectively, as well as for receptors and transporters in healthy individuals.

The PBPK models are composed of different types of information that are combined during model building and that can be used to generate simulations of different treatment scenarios. Such building blocks of information included in the model can be divided into organism properties, drug properties, and administration protocol and formulation properties, respectively (Figure 2).

Figure 2.

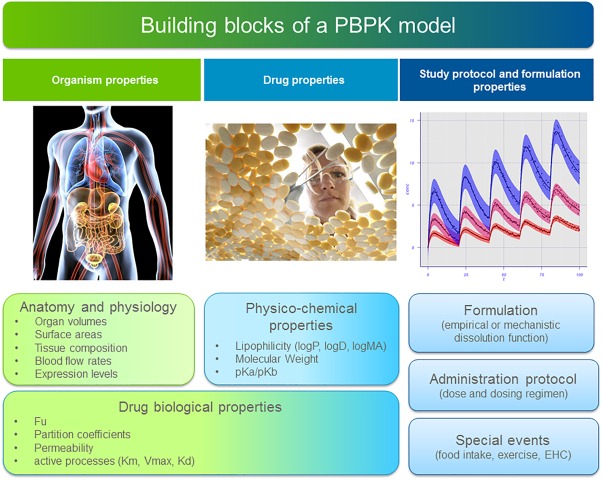
Representation of the general building blocks which can be part of a PBPK model. Some components may be optional depending on the model considered.

Figure 3.

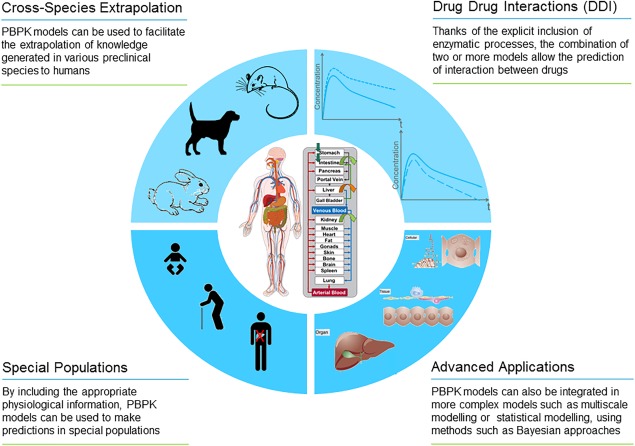
Schematic representation of the most common applications of PBPK modeling.

Organism properties are, for instance, organ volumes, organ composition, blood flows, surface areas, and expression levels. Such properties are dependent on the species or population considered. For example, in the case of special populations (e.g., diseased or pediatric populations) these organism properties take into account physiological differences between the special populations and the healthy adult reference population. By combining the drug properties with the anatomical and physiological features of the organism, it is possible to estimate the parameters for passive processes involved in distributing the drug in the body, such as, for example, permeation across membranes.

Drug properties include all parameters specific for the compounds under study. Notably, physicochemical properties such as compound lipophilicity, solubility, molecular weight (MW), and pKa values of a drug are fully independent of organism physiology. Drug‐biological properties (such as fraction of drug unbound, or tissue‐plasma partition coefficient), on the other hand, are drug‐specific but also defined by the interaction between the drug and the biological system itself, so they are dependent on both the drug and the organism properties.

Finally, information on the administration protocol and formulation properties is needed to define a PBPK simulation. Time‐related special events such as gallbladder emptying time or meal intake can also be included in the model and their impact on drug PK can be evaluated with the model.

The use of complex full‐blown PBPK models was recently facilitated by the development of several commercial platforms that integrate physiological databases and implement PBPK modeling approaches, such as GastroPlus (Simulations Plus, Lancaster, PA), SimCyp (SimCyp, Sheffield, UK), and PK‐Sim and MoBi (Bayer Technology Services, Leverkusen, Germany). These commercial PBPK modeling platforms provide a generic model structure for the physiology of predefined species and populations. They all include physiological databases that are combined with compound‐specific information as well as biometric data, and are used to parametrize a PBPK model on a whole‐body level.

In previously published tutorials, Jones and Rowland‐Yeo4 introduced some of the basic concepts of PBPK as well as the use of PBPK in drug discovery and development, while Maharaj and Edginton5 described the use of PBPK in pediatric clinical development. The aim of this tutorial is to cover the fundamental concepts of PBPK/PD models, focusing on their practical implementation in a typical PBPK model building workflow. In the next sections an overview of the information contained in the different building blocks of the model (section “Building blocks in PBPK modeling”) will be presented and then the different parameters included in the model structure will be discussed in more detail (section “Passive and active processes”). Finally, practical guidance on the different steps of the model‐building process will be provided (section “Best practices in PBPK model building”) and an example of PBPK/PD model will be discussed (section “Case study: Building a PBPK model for ciprofloxacin”).

Applications of PBPK modeling

Computational models provide an ideal platform for knowledge management since they offer the opportunity to collect, integrate, analyze, and store information. Ideally, in an integrative and iterative workflow such models can be used to generate working hypotheses from simulations. In turn, these hypotheses can then be tested in specifically designed experiments that may lead to a better understanding of the underlying processes and a refinement of the model. In the case of pharmaceutical applications, the main goals of PBPK modeling include (Figure 3): generating and testing a mechanistic understanding of the physiological processes that govern an observed drug behavior; translating the understanding to novel settings (e.g., to a different population); identifying an ideal therapeutic regimen; and optimizing risk–benefit ratios. In fact, any deviation between the model simulation and the data can provide insights into the mechanisms of the underlying processes that may not yet be reflected in the existing model.

Another important application of PBPK models are extrapolations to novel clinical scenarios such as different treatment schedules or patient subgroups. Notably, translation to novel therapeutic designs can usually be achieved by only changing single or limited sets of parameters. Extrapolations to different species or specific populations, in contrast, require knowledge of the sets of parameters characterizing the physiological properties of the species or particular patient cohort of interest.6

Typical applications of PBPK modeling include but are not limited to:

• Pediatric extrapolations,5, 7 where, with the support of the US Food and Drug Administration, a reference PBPK model for an adult population is scaled to specific life stages in children.

• Extrapolations to diseased populations, e.g., hepatically impaired cirrhotic patients.8

• Evaluating the effect of possible drug–drug interactions (DDI), e.g., by considering competitive inhibition of a metabolizing enzyme.9

• Scaling between different treatments scenarios by simulating specific dosing schemes.10

• Assessing the impact of different drug formulations by modifying corresponding compound/formulation parameters.11

Advanced applications include cross‐species extrapolation,12, 13 multiscale modeling,14, 15, 16 and statistical modeling using methods such as Bayesian approaches.17

Pharmacodynamic modeling

PBPK models offer a mechanistic framework to quantify the pharmacodynamic (PD) effect of a drug through coupling to simulated on‐ and off‐target tissue concentrations. The final result in this case would be a PBPK/PD model. An example of such a model is discussed in the ciprofloxacin case study presented in section “Case study: Building a PBPK model for ciprofloxacin” of this tutorial. Since different organs are explicitly represented in PBPK models, on‐ and off‐target tissue exposure can be directly quantified. This enables a consideration of therapeutic or toxic effects by coupling of PD to the corresponding PBPK models. To this end, tissue concentration profiles simulated with PBPK models may be used as input for downstream PD models. Notably, this coupling of PK and PD results in a multiscale PBPK/PD model that simultaneously describes drug ADME at the whole‐body level and the resulting drug effect at the cellular or tissue scale.

In the simplest case, PD models may represent simple proliferation models quantifying, for example, bacterial growth in infection biology18 or tumor growth in oncology.19 Given the ever‐growing number of systems biology models at different scales of biological organization, the PD disease or toxicity models may be largely expanded. Examples of such detailed PBPK‐based models include glucose‐insulin regulation in diabetes,10 management of endometriosis,20 acetaminophen intoxication,15 drug‐induced liver, injury21 or model‐based design and analysis of antithrombotic therapies.22 Ultimately, such PBPK/PD models aim for a mechanistic and physiological representation of systems interactions within the body,23 thereby providing an important toolbox for disease or toxicity modeling in quantitative systems pharmacology.

BUILDING BLOCKS IN PBPK MODELING

Anatomy and physiology

The physiology of the organism of interest is essential prior knowledge in PBPK modeling and relevant organs are explicitly included in the model. Each organ is represented by its anatomical and physiological properties; for example, volume, tissue composition, and perfusion blood flow rates. Furthermore, in some cases each compartment can be further divided into subcompartments, such as plasma, interstitium, cellular space, and red blood cells. Structurally, these subcompartments are the lowest level of structural differentiation in PBPK models and, for example, enzymatic processes can be localized in the relevant intracellular compartment to which the extracellular space can be connected by passive diffusion and additionally by active drug transport, where required. Without subcompartmentalization certain effects such as permeation limited metabolization within the liver may not be represented. Blood flow governs mass transfer within the body, and its rate is specific to each organ. Where necessary, a more detailed mechanistic description of a subset of organs can be included in the model; for instance, to obtain a more accurate description of the distribution in the brain,24 liver,25 kidney,26, 27 or lung,28 or describe in detail the process of intestinal absorption.29, 30, 31

Generally, two blood compartments, arterial and venous blood, connect the organ compartments in a PBPK model. Yet in clinical practice it is common to sample blood only from the superficial veins of patients, e.g., the antecubital vein. Thus, the measurements collected in peripheral veins present a concentration that may differ significantly from both arterial and central vein compartments, making the comparison of model predictions with collected data difficult. To solve this discrepancy, Levitt32 proposed a model in which an additional organ representing the tissues drained by the antecubital vein was added such that the concentration in the peripheral venous blood can be described. Based on this model, a peripheral venous blood compartment has also been included in some PBPK software tools.12, 33

Gastrointestinal transit and absorption models

For an orally administered drug, a combination of physiological, compound, and formulation‐related aspects comes into play. These affect the relevant parameters such as solubility, dissolution rate, and intestinal permeability.

From a general perspective, the gastrointestinal (GI) tract can be divided into several segments based on their anatomical and functional role: stomach, small intestine (duodenum, upper and lower jejunum, upper and lower ileum) and large intestine (cecum, colon ascendens, colon transversum, colon descendens, sigmoid, and rectum). Each of these segments can be further divided into zones representing the lumen and gut wall, which can in turn be divided into mucosal and nonmucosal tissues. The separation of the mucosal tissue from the remaining part of the gut wall allows the absorption processes to be described in a realistic manner, reflecting the localization of active processes such as gut wall metabolism in the respective tissue.34

After oral administration, the drug is transported along the lumen of the intestine according to a transit function. It can enter the mucosa of the corresponding segment either by the transcellular route (passing via the enterocytes into the intracellular space) or by paracellular diffusion into the interstitial space of the mucosa. The paracellular route has been shown to contribute significantly to the overall intestinal absorption of a few small molecules such as acyclovir, cimetidine, and ranitidine.29 However, the paracellular route is in general considered to contribute only marginally to the intestinal absorption, mainly due to the small surface area fraction that allows paracellular permeation.35 During the transit through the lumen, the maximum concentration of the drug might be limited by the local pH‐dependent GI solubility, which can be calculated using the Henderson–Hasselbalch equation. The intestinal pH will also affect the degree of dissociation of the compound, and consequently the relative concentration of neutral vs. the charged form(s). In this case, the charged molecules have a lower permeability than the neutral form, and this should be also accounted for in the model.36

Drug properties

The second major type of input into PBPK models are compound‐specific parameters. These include the physicochemical parameters of the compound (e.g., MW, lipophilicity, solubility, and pKa values) that can usually be determined in vitro. Lipophilicity is a key parameter that, together with the MW, is used to calculate the membrane permeability of a drug. The MW is, in this context, a surrogate measure for the size of the molecule. Since halogen atoms in particular contribute less to the molecular volume than expected from their atomic weight, a correction term can be applied to obtain an effective MW, which is a better representation of the size.36 Particularly relevant for oral administration, drug solubility determines the availability for absorption of a compound in the GI tract, while pKa values are used to calculate pH‐dependent changes in drug solubility. Pharmacokinetic parameters, such as fraction unbound, are likewise compound‐specific, yet they also depend on the organism. These basic values are frequently used together with physiological parameters to calculate other parameters that are much more difficult to measure but can be used immediately to quantify the drug mass balance in PBPK models. For example, tissue–plasma partition coefficients quantifying the distribution of a compound are calculated from MW, lipophilicity, fraction unbound, and pKa values, depending on the distribution model used (see below). Fraction unbound, the fraction of a drug not bound to plasma proteins, strongly influences drug distribution and clearance since only the available free fraction of a compound diffuses into cells, where it might be metabolized. Also, only the free fraction of a compound is filtered for renal excretion. The fraction unbound can either be measured experimentally, estimated from the drug concentration, or predicted from the lipophilicity of the drug, respectively.37 Notably, all the aforementioned compound‐specific parameters contribute to the quantification of passive processes such as membrane permeation and organ/plasma partitioning. On the other hand, key parameters for quantifying active processes such as enzymatic activity (Vmax) must be obtained by a complementary approach. For example, parameters for an active process can be determined in vitro or fitted from in vivo data and then converted to the enzymatic rate or a different parameter.

Formulation

The development of oral dosage forms for new chemical entities is often the favored option in drug development. The design and development of such formulations can be supported by accurate mechanistic models that can simulate in vivo bioavailability. In vitro dissolution profiles in biorelevant media, such as the Fasted State Simulated Intestinal Fluid (FaSSIF) and the Fed State Simulated Intestinal Fluid (FeSSIF), have been established. When used in standardized in vitro dissolution test methods, such media allow simulating the in vivo disintegration and dissolution behavior of orally administered dosage forms.38 This dissolution profiles together with drug PK profiles can be used to establish an in vitro–in vivo correlation (IVIVC). Such correlation enables the estimation of in vivo concentration PK profiles from the in vitro dissolution profiles of different formulations, providing a tool for optimizing the administered dosage form with a minimal number of in vivo animal experiments or clinical trials.39

As an alternative to a direct correlation between in vitro and in vivo concentrations, it is possible to include dissolution functions in the GI compartments of PBPK models to account for the disintegration and dissolution processes in the GI tract.40 The inclusion of such dissolution profiles in GI physiological models and their combination with whole‐body PBPK models has been described in the literature.30

Routes of administration and administration protocols

The administration protocol includes the (1) route of administration, (2) amount of compound (dose), and (3) an administration scheme for multiple dosing. Usually, when comparing model simulation to available data, the administration protocol used in the model will match the one used in the study for which the data are under evaluation.

Various routes of administration can be considered in the model. This will define how the drug is absorbed and, partly, how it will be distributed in the body. Common administration routes are intravenous (i.v.) and oral (p.o.) administration, but also alternative routes such as inhalation, subcutaneous, intramuscular, topical, or ocular administration are used in PBPK models. Apart from i.v., when considering other administration routes, also mechanistic consideration related to local drug release and absorption from the administration site should be included in the PBPK model, for instance to describe the progressive drug release and diffusion from the injection site after intramuscular administration.

PASSIVE AND ACTIVE PROCESSES

In PBPK modeling, physiological parameters provide the structural scaffold of the model, but active and passive processes describe the actual distribution, excretion, and metabolization of the drug (mass balance). The most important passive processes are tissue permeation and organ/plasma partitioning. The underlying processes are calculated from substance‐specific surrogate markers, such as lipophilicity, to obtain, for example, permeability or partition coefficients. Different concepts for quantifying passive and active transport processes are described in the following sections.

Estimation of passive processes from physicochemical properties for small molecules

Distribution models

Small molecules can generally penetrate all kinds of tissues in the body. Experimentally, the quantification of this compound‐specific distribution is very labor‐intensive.41, 42 A major advance in PBPK modeling came with the use of calculation methods for organ/plasma partition coefficients, which describe steady‐state ratios of the concentrations in the blood or plasma and the surrounding tissue. Various concepts for mechanistic correlations have been developed for the in silico estimation of organ/plasma partition coefficients. Based on tissue composition, these coefficients can account for the distribution between drug‐binding tissue constituents, such as proteins or lipids, on the one hand, and water on the other. Although the principles are very similar in all cases, the calculation methods deviate with respect to the kind of parameters used and resulting in different values of tissue concentration (Figure 1 c). All known partition coefficient models assume that tissue is composed of a limited number of components, and they all include partition coefficients for water/protein and lipid/water. These two partition coefficients are usually calculated from so‐called surrogate in vitro measurements. The total organ/plasma partition coefficient is then calculated as a weighted sum of the partition coefficients for all of the components; the weights are the volume fractions of each component. Importantly, the distribution of a drug within aqueous and organic tissue components is always assumed to be homogenous and passive. The most widely used concepts for calculating organ/plasma partition are briefly introduced below:

• Poulin et al.43, 44 calculate the lipo‐hydrophilicity of tissue as a mixture of neutral lipids, phospholipids, and water. In addition to the volumetric tissue composition, fraction unbound (fu), lipophilicity (logP and logD), and pKa are used as compound‐specific input parameters. Here as well as in all the following concepts for the calculation of organ/plasma partition coefficients, fu quantifies specific reversible binding to proteins in plasma and tissue, whereas lipophilicity accounts for nonspecific binding to lipids.

• Rodgers et al. extended the concepts of Poulin et al. to electrostatic interactions at physiological pH.45, 46 These include binding of ionized and unionized drugs to acidic phospholipids and neutral lipids, respectively. Also electrostatic drug interactions with extracellular proteins are taken into account. Consequently, the partition coefficients are calculated taking into account the lipophilicity and pKa value of the drug and the pH values of the tissues.

• Berezhkovskiy47 modified the calculation method by Poulin et al. by accounting for peripheral drug elimination that results in a different volume of distribution.

• Willmann et al.48, 49 extended the concept of Poulin et al. by additionally considering proteins as a tissue component. Moreover, Willmann et al. use membrane affinity (logMA)50 to quantify partitioning between water and an artificial cellular membrane as a measure for lipophilicity by using an empirical equation.51 This model is implemented in the PK‐Sim software as the PK‐Sim standard distribution model.

• Schmitt52 developed a method for calculating the organ/plasma partition coefficient for organic compounds, by compartmentalizing tissue as water, neutral lipids, neutral phospholipids, acidic phospholipids, and proteins. This concept accounts in particular for electrostatic interactions between charged molecules at physiological pH and acidic phospholipids. Also for this distribution method, the partition coefficients are calculated taking into account the lipophilicity and pKa value of the drug and the pH values of the tissues.

As shown in Figure 1 c, different distribution models can be used to describe similar plasma concentration profiles of the drug but, because of the intrinsic nature of the models, they will generate different tissue concentrations. If tissue concentrations for the drug are not collected, when assessing target site drug exposure it should be kept in mind that the selection of the distribution model represents a fundamental assumption during model development. An inherent uncertainty should hence be taken into account in the predictions. Ideally, different distribution models should be available during model development to allow for full structural flexibility in this regard. It should be kept in mind that Figure 1 c represents a specific example for the theophylline molecule, and it should not be used to draw any conclusion concerning comparison of distribution models and tissue predictions since the simulated concentrations are largely dependent on the drug parameters used as input.

Permeability models

Diffusion across the vascular wall from plasma to interstitial space of the organs or diffusion across the cellular membranes of tissue cells or red blood cells determines how fast drug distribution takes place and can be rate limiting for distribution (permeation limited kinetics). In general, the diffusion across the vascular wall is assumed to be fast for small molecules. However, this assumption might not hold true for drugs with high protein binding or which are highly hydrophilic.53 Also in the case of large molecules (e.g., protein therapeutics) this assumption does not hold true (cf. section “Passive and active process for large molecules”).

The cellular membrane is the diffusion barrier between interstitial space and intracellular space or between blood plasma and blood cells. The rate constant describing the diffusion across the cellular membrane can be written as the product of the drug permeability (P) and the effective surface area (SA) of the cells. Methods to calculate the drug‐specific permeability depending on physicochemical properties like lipophilicity and MW can be found in the literature.54, 55 In order to calculate the effective surface area for different organ volumes, allometric scaling equations can be used.56

An important consideration in calculating the rate and extent of intestinal drug absorption is the intestinal permeability. There are several experimental techniques that are able to provide a relatively reasonable assessment of the intestinal permeability, e.g., artificial membranes,57 “intestine‐like” cell lines (e.g., Caco‐2 or MDK),58, 59 Ussing chambers,60 and in situ rat intestinal perfusion techniques (e.g., single‐pass intestinal perfusion).61 In humans, effective permeability in different regions of the intestine can be measured using single‐pass perfusion methods.35 An alternative approach for establishing the intestinal permeability is to use the physicochemical properties as a basis for calculations.1 Several models are available for this approach; for instance, the membrane affinity of a compound (defined as its equilibrium partition coefficient for water and immobilized lipid bilayers) and its effective MW can be used for such calculations, using a semiempirical equation.51

Estimation of active processes for small molecules

Active processes allow the inclusion of additional mechanistic details in PBPK models, since they can frequently be assigned to biochemical processes at the molecular scale. Examples of such processes are metabolization reactions, in which a molecule is transformed and modified, as well as transport processes, in which a compound is actively taken up or secreted into a specific tissue compartment. Quantification of active processes follows different concepts than the ones of passive processes, relying on either careful extrapolation of in vitro results to an in vivo situation or knowledge‐based adjustment of parameters that are difficult to measure experimentally. In general, all clearance processes presented can be formulated as, for, instance first‐order clearance kinetics or Michaelis–Menten kinetics. The Michaelis–Menten kinetics are often used to describe processes that can be saturated by the substrate concentrations; its equation is the following, with v representing the reaction rate, Vmax the maximum reaction rate, Km being the Michaelis–Menten constant and the substrate concentration [S]:

$$v=\frac{V\mathit{max}*[S]}{Km+[S]}$$ (1)

If [S] is significantly lower than Km, elimination kinetics can be considered linear (first‐order process) and the rate constant for the clearance process can be approximated by the ratio Vmax/Km.

Parameters included for active processes are typically rate constants for elimination or active transport processes (e.g., intrinsic hepatic clearance, Michaelis–Menten parameters K_m and V_max, or parameters describing specific binding, for instance, to a receptor k_on and k_off). Examples of such processes are metabolic elimination related to a particular enzyme, or transporter activity or drug distribution due to binding partners. Parameters that define active processes are usually extrapolated based on in vitro measurements,62, 63 when the necessary extrapolation factors for measurement settings are available, or fitted using in vivo data.64 In vitro–in vivo extrapolation (IVIVE) can be applied to the different stages of absorption, distribution, metabolism, and excretion (ADME) processes.

Intrinsic and total plasma clearance

Clearance is generally used to quantify elimination rates in liver, kidney, or other organs. At the body level, total plasma clearance (CL_tot, i.e., volume of plasma cleared per time unit) describes the sum of multiple clearance processes that occur simultaneously within multiple organs. Here, CL_tot is the apparent rate at which a compound is removed from the systemic circulation. In PBPK modeling, the relative contribution of each organ to CL_tot can be further differentiated by quantifying the specific elimination rate in each organ. In this case, the intrinsic clearance CL_int is used to quantify the intracellular activity of a metabolizing enzyme in different organs.65

In vitro–in vivo extrapolation of clearance

For liver clearance, numerous in vitro assays are available to estimate the enzymatic activity, and this clearance needs to be rescaled to the whole‐organ in vivo situation. For example, activity can be derived from recombinant cytochromes, human hepatocytes, or human liver microsomes. For an IVIVE, the experimentally measured specific activity needs to be multiplied by the amount of catalyzing agent (amount of cytochrome, number of hepatocytes, or amount of microsomal protein) per gram of liver tissue to obtain the specific intrinsic clearance per gram of liver. The ratio of V_max/K_m describes the intrinsic metabolic clearance for unsaturated conditions, which can be derived from in vitro studies in human liver microsomes. In the past, IVIVE was routinely conducted based on mean data disregarding interindividual variability. As an alternative approach, it has been proposed to estimate enzyme abundance and its variability, measured by immunoquantification, to allow a direct extrapolation to the population level.66, 67

The second main clearance route in the body is usually renal secretion. Total renal clearance can be derived from the fraction of a drug secreted in the urine. This value can be further differentiated into glomerular filtration, which describes the passive filtration rate of urine in the kidney, and tubular reabsorption and tubular secretion, which are driven mainly by active transport.

Protein abundance in active processes

Although the liver and kidney are the key secretory organs of the body, the expression of many enzymes and drug transporters is not limited to these two organs. One way to quantify the contribution of different organs to the total clearance at the whole‐body level is to consider the relative tissue‐specific expression of genes or proteins. Recently, a generic approach was proposed whereby gene expression is used as a surrogate for tissue‐specific protein abundance in PBPK modeling.3, 12 The catalytic activity of each process is generally quantified for each organ by Vmax (μmol/l/min). Notably, Vmax_j is the product of the catalytic efficiency kcat (1/min) and the overall concentration of the catalyzing protein E_0,j (μmol/l) in the corresponding organ j:

$$Vma{x}_j=kcat*E_{0,j}=kcat*E_0*e_{rel,j}=kca{t}^{*}*e_{rel,j}$$ (2)

This reformulation allows describing the tissue‐specific abundance of an enzyme or transporter (E_0,j) as the product of its overall concentration, E_o, and its relative expression, e_rel,j, in a specific organ j. While E_o is obviously not accessible experimentally, relative expression profiles (e_rel,j) across different tissues may be obtained from public databases.3 In the above equation, kcat* is a new parameter that combines the catalytic efficiency kcat and the overall concentration E_o. This parameter needs to be estimated through parameter optimization. Moreover, it should be noted that this reformulation reduces significantly the number of independent model parameters, since only a single parameter (kcat*) needs to be considered instead of assigning a catalytic efficiency Vmax_j separately for each organ. Please note also that the relative tissue‐specific abundance of an enzyme or a transporter may be approximated either through gene or protein expression, respectively,3 even though correlations of both are a matter of debate. This is because any posttranscriptional effect can be assumed to be largely protein specific, as such only impacting kcat*. The use of expression data to quantify relative tissue‐specific catalytic efficiency represents a complementary approach to the IVIVE of clearance processes.68 Likewise, drug elimination in first‐pass organs such as liver, lung, or GI as well as other organs can be described.

Figure 1 d shows the relative gene expression for a group of enzymes, receptors, and transporters in healthy individuals or cancer patients, respectively. Note that the relative expression is dimensionless following normalization to the tissue with the highest expression. As expected, cytochrome P450 expression is consistently largest in the liver and the intestines, while receptor expression is rather ubiquitous. In turn, transporter availability is similar to cytochrome P450 with an occasional small contribution in the kidney (MRP2, BCRP). Interestingly, CYP2D6 expression is higher in the large intestine than in the liver in two independent measurements (healthy subjects and cancer patients). To validate this observation protein expression data from the literature could be alternatively used for model building, instead. Only a limited number of organs or tissues are represented for illustration.

Receptor availability

The above‐described concepts use expression data to quantify catalytic efficiency but they are applicable to both enzymatic processes and drug transporters as well. Notably, the approach can immediately also be applied to estimate the abundance of receptors for different drugs, including antibody‐drug conjugates.69 Thus, the availability of specific drug binding partners can be quantified simultaneously in multiple organs; this has enormous potential for mechanistic consideration of target‐mediated drug disposition or clearance, as well as on/off‐target effects.

Passive and active processes for large molecules

Therapeutic proteins are an increasingly important class of drugs.70 PK/PD modeling of therapeutic proteins differs from those of small‐molecule drugs, mainly due to the differences in size.71, 72, 73 PBPK models as well must therefore take into account the special mechanisms that govern the pharmacokinetics of protein therapeutics, mechanisms that can often be neglected for small molecules. Both the exchange of drug across the vascular endothelium and the return of drug by the lymph flow from the interstitial space of the organs to the systemic circulation are important phenomena for therapeutic proteins. These two processes influence the volume of distribution for proteins, and are generally considered in PBPK models of therapeutic proteins.74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84

Published PBPK models use various approaches to describe the extravasation of protein therapeutics. One commonly used is the two‐pore formalism,85, 86 which considers the barrier between the plasma and the interstitial space as a membrane consisting of two types of pores: few large ones and many small ones. Macromolecules are assumed passing through these pores by convection as well as by diffusion; convection being the predominant extravasation mechanism for large protein therapeutics such as antibodies or albumin.

Another relevant process for antibodies or other proteins (e.g., albumin fusion proteins) is the catabolism within endosomal space and the protection from catabolism by neonatal Fc receptor (FcRn), which is also often taken into account by more recently published PBPK models.76, 77, 78, 79, 80, 81, 82, 83, 84

In describing the lysosomal degradation of drugs and their recycling by FcRn, the organ representation used for small molecules is usually extended by adding a compartment for the endosomal space. This space represents the region within the endothelial capillary walls where catabolism and high‐affinity binding to the FcRn occurs (acidic environment). The fraction of drug that is bound to FcRn is recycled to the plasma and interstitial space, whereas the unbound fraction is subject to endosomal clearance. Additional processes can also be important and implemented if needed. Examples include target‐mediated disposition and clearance84 and immunogenicity.87, 88

BEST PRACTICES FOR PBPK MODEL BUILDING

Due to increasing application of PBPK modeling in drug development and regulatory submissions, there have been recent efforts by regulatory agencies, industry, and academia to discuss and develop best practices for establishing as well as reporting of PBPK modeling.89, 90, 91, 92, 93, 94 In this section, general recommendations for PBPK model building are provided (for information specific to applications for pediatric populations, see Refs. 5,95).

Compilation of available data and information

As a first step in model development, all available information on the drug regarding its ADME properties are gathered. This includes the drug‐specific parameters, which are used as input parameters, and the characterization of the organism or population. Default physiological parameters should only be changed if there is a mechanistic rationale, for instance, in the case of special populations. The physicochemical drug properties (see section “Drug properties”) are necessary parameters to inform the drug distribution. Besides these parameters, any further ADME information regarding, for instance, clearance processes, transporters, or specific binding partners are relevant in order to build physiologically plausible models. The appropriate level of detail in representing the relevant processes and the criteria for model evaluation depend on the particular aims, objectives, and applications of the model as well as on availability of data and information. Available experimental PK data are used to identify unknown or uncertain parameters as well as for model validation. Depending on their availability, data commonly used in PBPK model building includes time–concentration profiles of the drug in the plasma (for different preclinical species and/or humans, different application routes, different dosages, or applications schemes), time–concentration profiles of the drug in relevant tissues, the percentages of drug excreted via the urine and feces, mass balance data, and metabolites data (time–concentration profiles, excretion data). A scheme of the PBPK model‐building workflow for small molecule drugs is provided in Figure 4 .

Figure 4.

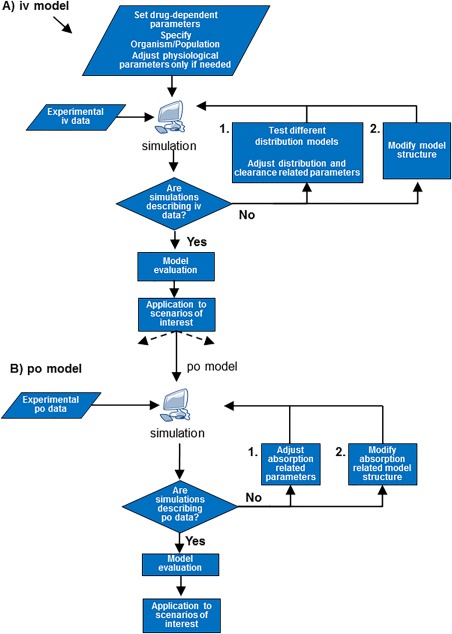
Flowchart illustrating the steps usually used in PBPK model building.

Establishment of the PBPK model for i.v. administration

As a first step, a method for calculation of organ/plasma partition coefficients, frequently referred to as distribution model, needs to be chosen to describe the drug distribution behavior. The distribution model selected for a certain compound should be able to consistently describe the compound distribution independently of the considered species or administration protocol. By comparing simulations with PK measurements in vivo after i.v. administration, different distribution models can be compared and clearance parameters can be estimated. The clearance parameters can be estimated from experimental in vivo data, i.e., plasma concentration–time profiles. Additionally, mass balance data might be used if different elimination pathways should be informed. Rates for metabolism processes might also be estimated using IVIVE approaches (see section “In vitro–in vivo extrapolation of clearance”). Surrogate compound parameters, like lipophilicity, are usually slightly adapted at this stage to obtain a good agreement with experimental i.v. data. There are no established rules regarding the extent of change that is reasonable, since this also depends on which lipophilicity measure is used as starting value. Even though a PBPK model may comprise several hundreds of ordinary differential equations, the number of independent model parameters for a new compound is usually small (in most cases, fewer than five per compound), due to the large amount of prior, independent physiological information that is incorporated (Figure 1 b). As in the case of the distribution models, also these compound‐specific parameters are usually kept unchanged across different species or administration protocols. If the selection of distribution models and adjustment of parameters are not sufficient to describe the i.v. data, this can be an indication that relevant processes are not yet taken into account in the model. In such cases, for instance, active transport or binding partners can be incorporated based on current knowledge or as testable hypothesis. Such additional processes might also be needed to explain features such as dose nonlinearity, the observed extent of clearance, or the drug distribution. When introducing additional processes, it is best to include as much experimental data as possible (e.g., K_m and K_d, values, abundance of enzyme, binding partner). It should be noted that data for different doses have to be available (showing dose‐nonlinearity) in order to be able to identify Michaelis‐Menten parameters, e.g., for transporters or clearances.

Establishment of the PBPK model for oral administration

Once an i.v. model is established, a model for p.o. administration (or for other extravascular routes) can be established. In this step none of the parameters that influence distribution or metabolism/excretion should be further modified and only those parameters that influence the oral absorption should be varied. Typical parameters to be estimated during development of a p.o. model are intestinal permeability and parameters related to meal events. In addition, formulation‐related parameters describing drug release as well as solubility might be adjusted, especially if aqueous solubility rather than FaSSIF and FeSSIF solubility were used as starting values. After that, additional absorption‐related processes, such as enterohepatic recycling (EHC), might be included if relevant for the drug under consideration. The stepwise approach of i.v. and p.o. (or any extravascular administration) model building is described to stress that during the establishment of a model including drug absorption, the information regarding distribution and clearance processes from the i.v. data should be used in order to be able to identify the parameters relevant for absorption. Note that in some cases the proposed strictly consecutive building of i.v. and p.o. PBPK might not be the best approach; for instance, if the i.v. model incorporates processes that are also relevant for oral absorption, e.g., uptake transporters. In such cases, it might be preferable to perform parameter identification using the i.v. and p.o. data simultaneously.

As mentioned, i.v. data are highly valuable, since they allow informing distribution and clearance processes independent from the drug absorption. Depending on the modeling purpose and the needed model precision, a PBPK model might also be developed using p.o. data only. Taking into account data on drug absorption, metabolism, and mass balance data, it is necessary to rely on the PBPK or IVIVE methods regarding prediction of absorption or clearance. If human i.v. data are missing, a human p.o. model might be scaled from an animal model that was established using i.v. as well as p.o. data. Without using i.v. data, the model uncertainty can be considerably higher depending on the BCS classification of the drug and if transporters or gut‐wall metabolism are involved.

Overall model evaluation

After model development, the model quality should be evaluated. This step should address whether the model fits its purpose. As such, the outcome of the evaluation depends on the goal of the modeling project. The following criteria or tests can be used in evaluating the model.

Agreement of modeling outcome with experimental data

Usually, a model is evaluated by visually comparing simulated vs. experimental concentration–time profiles (for plasma and, if available, for other tissues), focusing on the absolute concentrations and the dynamic shape of the PK profile or by means of error functions such as root‐mean‐square deviation (RMSD), the area under the curve (AUC) error,12 or the concordance correlation coefficient.16 Additionally, typical PK parameters like C_max, t_max, AUC, and t_1/2 can be compared between data and simulation during model evaluation. While comparing model simulations and experimental data, it should be considered that both are subject to uncertainty, and also experimental data might be critically reevaluated. In addition to data used for model building, further data can also be considered as external validation to assess consistency of model prediction.

Consistency of PBPK models for different doses, across species, special populations, and compounds

An important cross‐check for model validation is the consideration of different doses. Deviations in estimations for dose levels that had not been considered during model development point to structural shortcomings of the model. The drug‐dependent parameters as well as the calculation methods for distribution and cellular permeability should be the same across all species for a certain drug. If this is not possible, a plausible physiological explanation, as, for instance, species‐specific processes, should be discussed. If PK data for special populations, such as hepatically or renally impaired patients, are available, the model can also be evaluated using these data after changing the physiological parameters accordingly. The model might additionally be evaluated for consistency across compounds for which the same processes are relevant for the ADME properties. For example, if a saturable receptor binding was implemented as a relevant process into a PBPK model, it could be checked if the receptor concentration is the same in a PBPK model of a reference compound binding to the same receptor.

Sensitivity analysis or best‐ and worst‐case scenarios

In order to assess uncertainties in model results, it is recommended to perform a sensitivity analysis for relevant parameters. Such sensitivity analysis can be performed, for instance, on uncertain parameters for active processes included in the PBPK model or to all parameters in the model, in order to identify the most sensitive parameters for a specified model output (e.g., plasma concentration or PK parameters). Additionally best‐ and worst‐case scenarios can be simulated in order to evaluate the effect of changing uncertain parameters to extreme values within the experimental and physiological uncertainties. Uncertainties regarding underlying mechanisms can be assessed by simulating the respective model alternatives. The results of the sensitivity analysis or best‐ and worst‐case scenarios can be used to assess if the conclusions of modeling work are robust.

CASE STUDY: DEVELOPING A PBPK/PD MODEL FOR CIPROFLOXACIN

In order to illustrate the various steps of PBPK model development in a practical example, the construction of a PBPK model for the antibiotic ciprofloxacin (CIP) will be described in this section. Following the best‐practices section above, the experimental data needed for parametrization of the basic model structure will be discussed and it will be shown how both i.v. and p.o. administration of the drug may be systematically considered during model establishment. Finally, an empirical PD model of CIP treatment of E. coli infections18 will be coupled to the PBPK model. This resulting PBPK/PD model will be then used to simulate the therapeutic effect of different dosing schemes. The individual steps in model development are provided as a hands‐on tutorial in the Supplementary Materials. The final modeling example shows prototypical demands and applications of PBPK modeling in a pharmaceutical development program.

The first step in PBPK model building is gathering and assembling existing information. In this regard, the basic physicochemistry of the drug is of particular importance (Table 1 1A A). The physicochemical information in Table 1 1A A can be plugged directly into a PBPK software tool, where it is used to calculate all indirect PBPK model parameters from the models, as explained above. Notably, the information provided in Table 1 1A A, together with the exhaustive collections of physiological parameters integrated in PBPK software tools, is sufficient to obtain a preliminary, yet fully parametrized initial model regarding absorption and distribution processes.

Table 1A.

Physicochemical parameters

Parameter	Value	Parameter	Value
logP	0.95	pKa (acid)	6.1
MW	331 g/mol	pKa (base)	8.6
MW (effective)*	314 g/mol	fu in human	0.67
Solubility	6.18 mg/ml

These parameters represent the a priori input parameters for the drug.

*CIP contains a fluorine atom that leads to a reduction of the effective MW.

In the case of CIP, various clinical studies have been performed to identify physiological processes governing drug ADME. The following assumptions were made in the model: (1) CIP is metabolized via CYP1A2,96 (2) CIP is secreted into bile ducts in the liver,97 and (3) CIP is subject to significant renal elimination.98 In this regard, it is interesting to note that the rate at which CIP is excreted in the kidney cannot be explained by passive glomerular filtration alone; active tubular secretion must also contribute to the excretion process. In the case of a novel compound, the parametrization of such active physiological processes requires either IVIVE of physiological parameters in combination with dedicated scaling factors68 or identification of the model parameter using targeted experimental mass balance and excretion data. For the CIP example discussed here, it was assumed that the contribution of each of the three above‐mentioned physiological processes has been determined before (Table 1 1A B). Because CIP demonstrates dose linear PK,99 all three processes are quantified by first‐order kinetics.

Table 1B.

Metabolization and excretion

Process		Parameter
CYP1A2 metabolization	17 ml/min (intrinsic clearance)
Biliary secretion	1.03 ml/min/kg
Renal excretion	GFR specific: 0.266 ml/min/g of organ TBS: 0.57 l/min

These parameters have been estimated from the plasma drug concentration. GFR, glomerular filtration rate; TBS, tubular secretion

Assuming a mean standard individual (i.e., an individual with average demographic covariates) and a given administration scheme, the resulting PBPK model can be used for a first simulation of drug plasma concentrations. As outlined in the best‐practice section above, the establishment of a PBPK model for an i.v. administration is usually a reasonable first step, since it makes it possible to ignore all effects related to absorption in the GI tract. Here, clinical data for i.v. administration of 200 mg CIP are considered.100 For initial PBPK model building, the physicochemical properties of CIP (Table 1 1A A) are first integrated into the PBPK software to calculate the basic distribution model. In a second step, parameters for physiological metabolization and excretion processes were estimated from experimental PK data (Table 1 1A B). Whereas renal excretion and biliary secretion are solely linked to single organs, i.e., kidney and liver, respectively, enzyme‐mediated metabolization may simultaneously occur in tissues throughout the body. For the CIP model, relative CYP1A2 abundance was quantified, using tissue‐specific gene expression as a surrogate for protein availability3 (Figure 1 d). In the resulting PBPK model, the distribution, metabolization, and excretion of CIP is structurally represented. The standard distribution of PK‐Sim was identified as the most accurate distribution model, and the associated model parameters are quantified. Since the main focus is on intravenous administration during initial establishment of the model, as mentioned, it is reasonable to ignore oral absorption at this time. Note that a mean patient is usually represented by the collection of physiological PBPK model parameters used as such quantifying the basic model structure. The only information missing at this point is the CIP dose administered intravenously. In accordance with the experimental PK data, an i.v. dose of 200 mg CIP is considered here. Figure 5 a shows the result of a 24‐hour simulation of the i.v. CIP PBPK model, as well as the corresponding observed PK plasma data.100 In an actual pharmaceutical development program, this single step can potentially involve several iterations of parameter optimization, and bring about the identification of structural changes in the model.101

Figure 5.

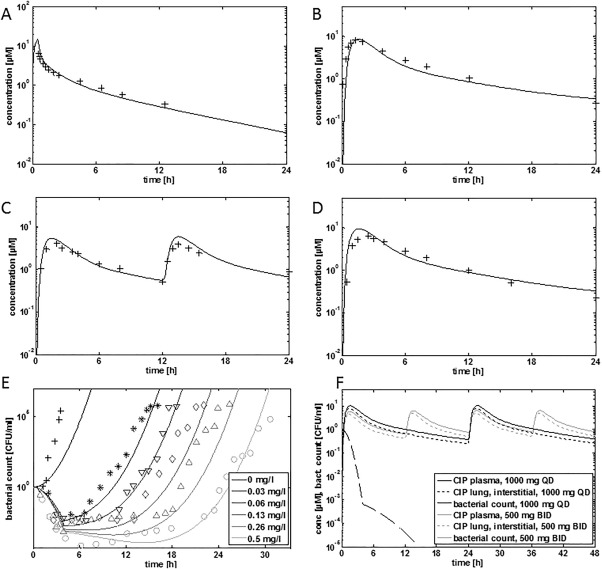
(a) PBPK simulations for 200 mg CIP (i.v.).100 (b) PBPK simulation for 750 mg CIP (p.o.).100 (c) PBPK simulation for 500 mg b.i.d. (p.o.).18 (d) PBPK simulation for 1,000 mg q.d. (p.o.).18 (e) PD simulations with an adaptive Emax model that describes time‐kill profiles of E. coli (11775) in the context of various in vitro doses of CIP.18 (f) PBPK/PD simulations. q.d., once‐a‐day dosing; b.i.d., twice‐a‐day dosing.

In the next step, the oral administration of CIP was considered. The dataset from the study by Davis et al.100 is particularly well suited for this purpose because it contains a crossover study in which CIP was administered to the same patients both i.v. and p.o. The missing model parameters for oral administration are relevant only to absorption in the GI tract. First, the specific drug formulation needs to be considered. A Weibull function was assumed to quantify dissolution of the tablet (Table 1 1A C). Together with formulation release, the physicochemical solubility of CIP (Table 1 1A A) and the estimation of the intestinal permeability (Table 1 1A C) are sufficient to quantify absorption of a CIP tablet in the GI tract. As previously discussed, the physiological processes implemented above for the i.v. administration remain unchanged, such that CIP ADME can now be fully represented with the PBPK model. Figure 5 b shows the result of a 24‐hour simulation of the p.o. CIP PBPK model, as well as the corresponding PK plasma data for an oral CIP dose of 750 mg.100 The resulting PBPK model can now be used to assess different administration schemes, to simulate virtual populations, or to extrapolate the data to special populations.5 As a validation of model predictions, the model was used to simulate the administration of 500 mg b.i.d. and 1,000 mg q.d., and the model predictions were compared with the data available in the publication by Schuck et al.18 As can be seen from Figure 5 c,d, the model is able to describe both doses as well.

Table 1C.

Oral absorption.

Process	Parameter/Function
Drug dissolution in the GI tract (Weibull)	time (50%):4 min lag time: 0 min Shape: 0.8
Transcellular intestinal permeability	1E‐06 cm/min
Small intestine transit time	4h

These parameters have been estimated from the plasma drug concentration.

Having established a PBPK model for i.v. and p.o. administration of CIP, as next step such model was applied to further PD analyses. As mentioned above, CIP is routinely used in clinical practice for the treatment of E. coli infections. An adaptive in vitro Emax model for CIP treatment of infections with the microbial strain E. coli (11775) was previously established.18 The model allows the description of microbial growth as well as CIP‐mediated inhibition such that time‐kill profiles can be mechanistically analyzed. The model hence quantifies growth in the absence as well as in the presence of CIP treatment, and shows an initial phase of rapid killing followed by the development of an adaptive resistance that slows the killing rate in the presence of CIP.

$$\frac{dN}{dt}=\left(k-\frac{\left(k_1\cdot (1-\frac{C_r}{I{C}_{50}+C_r}\right)+k_2}{E{C}_{50}+C}\cdot C\right)\cdot \mathrm{N}\cdot \left(1-e^{z\cdot t}\right)$$ (3)

Here, N is the bacterial count (CFU), k is the growth rate, k₁ is the initial kill rate constant, k₂ is the permanent kill rate constant, C is the lung interstitial concentration, i.e., the site of infection, and z accounts for the initial lag phase (Table 1 1A D). C_r is the drug concentration inducing adaptive resistance (Table 1 1A E):

$$C_r=C_0\cdot \left(e^{-k_{e\cdot }\cdot \left(t-t_{lag}\right)}-e^{-k_{ecr\cdot }\cdot \left(t-t_{lag}\right)}\right)$$ (4)

Table 1D.

Bacterial growth model

k (h−1)	k1 (h−1)	k2 (h−1)	EC50 (mg/l)	IC50 (mg/l)	z (h−1)
7.76	10.8	8.4	0.0035	0.00047	0.09

These parameters are provided in the literature (95).

Table 1E.

Adaptive resistance

tlag (h)	kecr (h−1)	ke (h−1)
4	10	0.014

These parameters are provided in the literature (95).

In this equation, C₀ is the initial CIP concentration in the experiment, k_e is the simulated elimination rate constant, k_ecr is the decline of the adaptive resistance (Table 1 1A E), t_lag is the lag time until development of adaptive resistance sets in, EC₅₀ is the concentration of CIP that gives half‐maximal response, and IC₅₀ is the concentration at 50% of maximum resistance. The adaptive Emax model has been validated using in vitro data on the growth of E. coli in the presence of different in vitro CIP concentrations18 (Figure 5 e).

The CIP PBPK model and the PD model for CIP treatment of respiratory tract infections of E. coli infections can now be combined to generate a full‐blown PBPK/PD model. In a previous PK/PD study, an initial CIP concentration was calculated from a simulated 24‐hour area AUC vs. time curve (AUC₂₄)/MIC ratio (C_0' = 2.43 mg/l).18 Using the lung interstitial concentration in the PBPK/PD as input in the adaptive E_max model, the therapeutic effect of 1,000 mg once‐daily (q.d.) and 500 mg twice‐daily (b.i.d.) of CIP was simulated for this bacterial strain (Figure 5 f). As reported before, the time kill curve for both dosing regimens show an equally effective decrease in CFU/ml >5 log units over the first 24 hours.18 As also reported in the literature, this is related to the use of an E. coli strain extremely sensitive to CIP, for which the 500 mg b.i.d. dosing regimen was already high enough to promote maximum bacterial killing. Notably, the presented PBPK/PD model could now be the starting point for further investigations involving, for example, dedicated disease models of bacterial infections in specific tissues or usage of interstitial or intracellular target tissue concentrations as effective input concentrations.

SUMMARY

In conclusion, PBPK models can be a valuable support in drug development, in particular considering the possibility to generate a priori simulations. As a consequence, they are increasingly used in pharmaceutical companies and regulatory agencies like the US Food and Drug Administration. Such model development is possible, on the one hand, thanks to the collection of physiological and anatomical information as well as models that relate the physicochemical properties of a molecule to its permeability and partition properties. On the other hand, during the model building process model assumptions should be carefully considered and components included in the model should be in agreement with physiological and pharmacological information available for the considered compound. Such assumptions should also be clearly kept in mind when using the model for simulation and extrapolation. Together with assumptions regarding the processes included in the model, also assumptions relative to the physiological and anatomical information incorporated from the database should be carefully evaluated, in particular when considering diseased populations for which in many instances such information is not available or extremely variable.

Supporting information

Supporting Information

Supporting Information

Supporting Information

Supporting Information