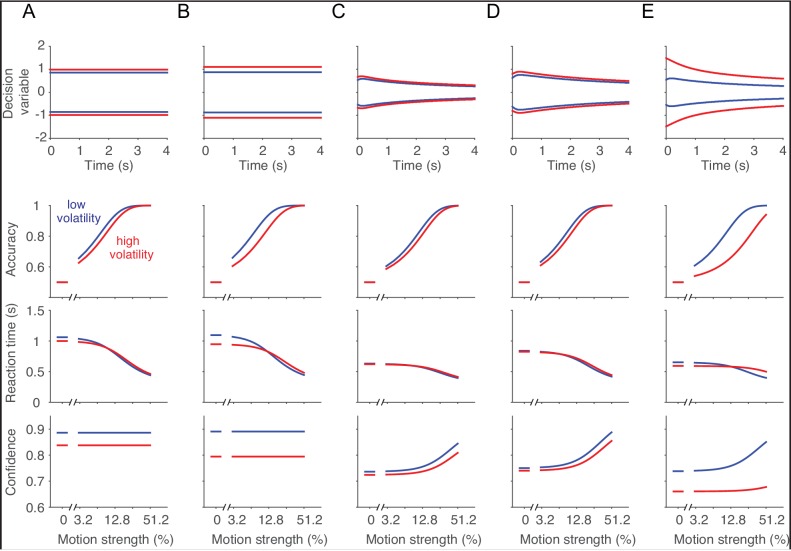
Appendix 1—figure 1. Normative decision model.
From the model comparisons we concluded that the volatility manipulation affected the noisiness of the momentary evidence without consistently affecting the parameters of the decision making process. However, it is unclear from these analyses what an optimal decision maker would do if the volatility condition were known. Therefore, we used dynamic programming to find the decision policy that maximizes average reward (Rao, 2010; Drugowitsch et al., 2012), for a variety of combinations of task parameters. The following examples are meant to convey intuitions about how parameters can change to maximize overall success per unit time. (A) Optimal solution for an experiment in which there is just one nonzero motion strength. Notice that the optimal bound height for low and high volatility trials is independent of time, consistent with a well known property of Wald’s sequential probability ratio test (Wald and Wolfowitz, 1948). The high volatility condition invites a slightly higher bound but not so much to overcome the faster decision times induced by greater noise (A, third row). Unlike the experimental observation, the normative solution assigns lower confidence under high volatility (A, bottom). (B) If the noise level associated with the high volatility condition were exaggerated further, the optimal solution would predict a greater increase in the bound height, thereby compensating for the additional noise. The bound height for the low volatility condition should increase as well. (C) In the situation we study, there are many levels of difficulty which are randomly interleaved across trials. In this situation, the optimal solution asserts a time-dependent collapse of the bounds toward lower magnitude of accumulated evidence (Drugowitsch et al., 2012). As in the single coherence case, the high volatility condition should induce an increase in bound height at all times, relative to the low volatility condition. Notice, however, that the optimal solution would lead to lower confidence under high volatility—contrary to what we observed empirically. The same pattern holds if there is a substantial time penalty after an error (D) and if the variance in the high volatility condition were exaggerated to six times that of the low volatility condition (E).