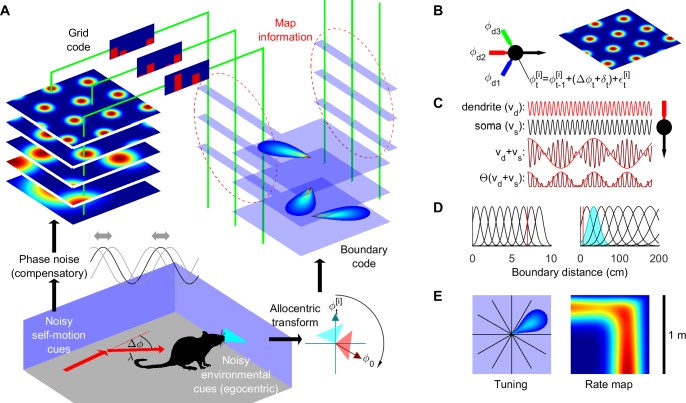
Fig 1. Probabilistic spatial learning using grid and boundary cells.

(A) Self-motion (angular and linear displacement, Δϕ and λ) and boundary inputs (transformed via estimated heading, ${\varphi }_t^{[i]}$) shift grid phase and activate boundary cells, respectively, forming associative maps (dashed ellipses) during learning. (B) Self-motion phase signal is integrated along each preferred direction of the grid cell (ϕ_d1, ϕ_d2, ϕ_d3) via plane wave oscillators, whose coincident activity leads to a hexagonal tessellating spatial grid in the absence of noise. (C) An example of plane wave oscillators produced by the interference between dendritic membrane oscillations, v_d = cos(ω_dt), and somatic membrane oscillations, v_s = cos(ω_st), producing an approximately sinusoidal rectified oscillation, Θ(v_d + v_s), where Θ denotes the Heaviside function [14]. (D) Distance tuning functions of short-range (left) and long-range (right) boundary cells (red line—maximum boundary detection distance without vision). (E) Firing rate map (right) of boundary cell with example tuning direction (E, left) and distance (D, shaded). See also S1 Fig and S1.1 Text.