Fig. 1. Measuring the time-gated reflection matrix.

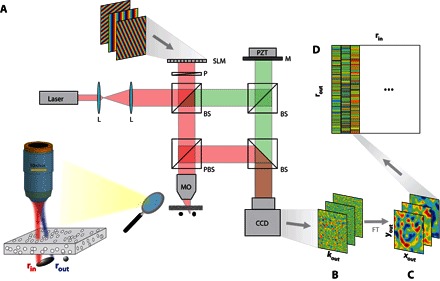
(A) A femtosecond laser beam (center wavelength, 810 nm; bandwidth, 40 nm) is shaped by an SLM acting as a dynamic diffraction grating. A set of incident plane waves is thus emitted from the SLM and focused at a different position in the focal plane of an MO (NA, 0.25). The backscattered wave field is collected through the same MO and interferes with a reference beam on an CCD camera. The latter one is conjugated with the back focal plane of the MO. The amplitude and phase of the wave field are recorded by phase-shifting interferometry (5). The time of flight t is controlled by the length of the interferometric arm and is matched with the position of the focal plane. Experimental setup: L, laser; P, polarizer; MO, microscope objective; BS, beam splitter; PBS, polarized beam splitter; PZT, piezo phase shifter; M, mirror. (B) For each input-focusing point r_in, the reflected wave field R(r_in,k_out) is recorded in the k space. (C) A two-dimensional Fourier transform yields the wave field in the real space R(r_in,r_out), where r_out represents the output-focusing point in the focal plane. (D) For each incident-focusing point r_in, the recorded wave field is stored along a column vector. Finally, the set of column vectors forms the reflection matrix R = [R(r_in,r_out)].