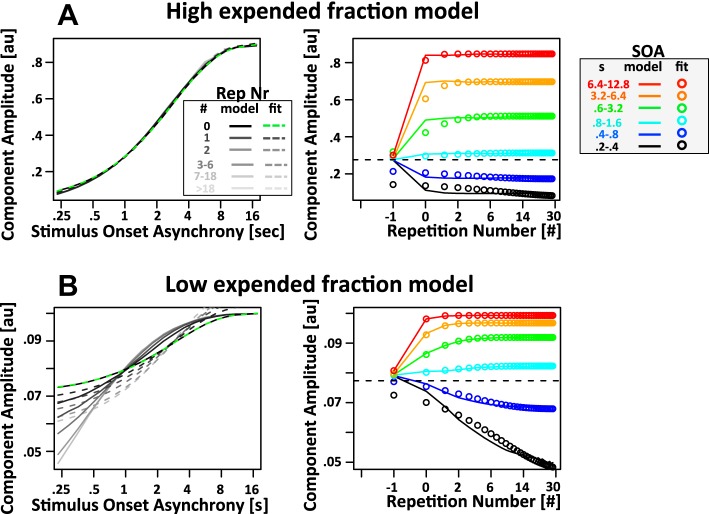
Fig. 2.
Properties of limited resource model. Shown are simulated responses from the limited resource model with a recovery time constant τ of 2 s. A and B, left: simulated component amplitude as a function of SOA split by repetition number (Rep Nr; black and shaded lines). Right, response amplitude as a function of repetition number split by SOA (black and colored lines). Note that a repetition number of 0 corresponds to the tone following the first time a specific SOA is presented in a series of identical SOAs. Furthermore, a repetition number of −1 corresponds to all tones that preceded tones with a repetition number of 0. Because of the design of the experiment, these trials have a random SOA. Hence, the component amplitude for a repetition number of −1 is approximately identical to the mean over all trials (dashed line). An exponential decay function with time constants of 2 s (same as recovery time constant τ) was fit to the simulated data. In left panels, the fits with λSOA = 2 s are indicated by dashed lines; in right panels, the fits with λRep# = 2 s are indicated by colored circles. Note the logarithmic x-axis in both cases. As a result, the exponential recovery functions have a somewhat unusual sigmoidal shape. A: in the high expended fraction model, the effect of SOA is largely independent of the number of repetitions of a particular SOA. The dependence of component amplitude on SOA is captured well by the fits with λSOA = 2 s. In contrast, component amplitude as a function of repetition number reaches an asymptote almost instantaneously with the very first use of a particular SOA (repetition number = 0). Hence, the fits with λRep# = 2 s do not capture the simulated data (see circles for deviation of fit from simulated data). B: the low expended fraction model reveals a somewhat complementary pattern of results: the dependence of amplitude on repetition number is captured reasonably well by fits with λRep# = 2 s, especially for tones with SOA above 0.4 s (blue, cyan, green, orange, and red color). Fits become even better because expended fraction is further reduced toward 0 (data not shown). In contrast, the dependence of amplitude on SOA is not captured by fits with λSOA = 2 s (note the stark misfit of the dashed lines). The only exception is the data for the first presentation of a particular SOA (repetition number = 0). In this case, the dependence of amplitude on SOA is captured perfectly by a time constant λSOA = 2 s (green dashed line).