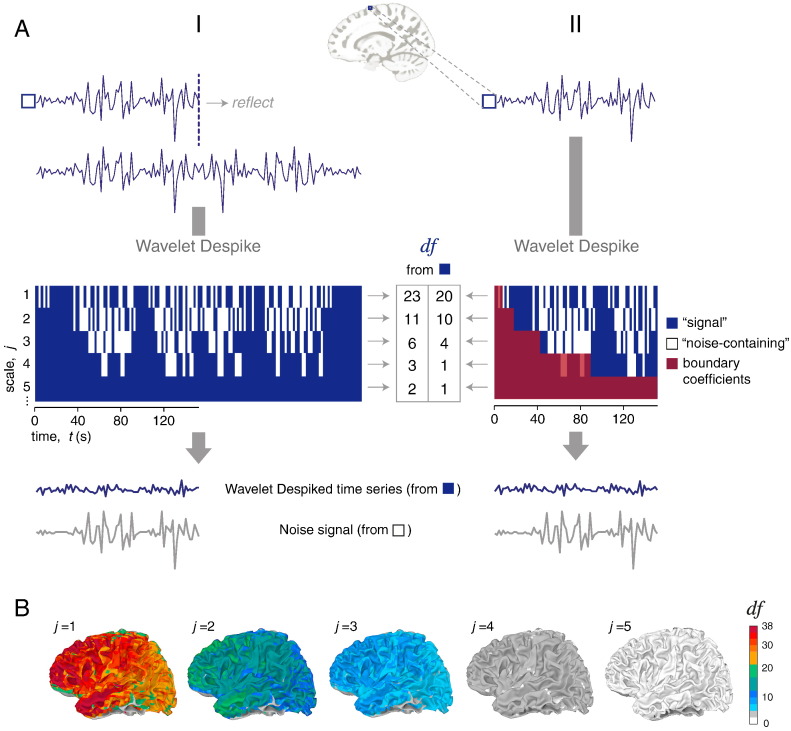
Fig. 1.

A wavelet-based estimator of the (effective) degrees of freedom, df, in functional MRI time series. Each voxel time series is processed using the wavelet despiking algorithm. The first step in this algorithm is computing the maximal overlap discrete wavelet transform (MODWT) of the time series. (A) Column (I) shows the MODWT computed using the reflection boundary, and (II) shows the same for the periodic, or circular boundary. This step converts the time series into a matrix of scale (j) vs. time (t). Denoising is conducted on this matrix to produce a final binary matrix indicating coefficients affected by non-stationary events (“noise” coefficients ${\tilde{W}}_{\varphi ,j,t}$ shown in white) and unaffected coefficients (“signal” coefficients ${\tilde{W}}_{\alpha ,j,t}$ shown in blue). For more details on the method, see Section 2.3 and Patel et al. (2014). The df are estimated from the “signal” coefficients as described in Eqs. (5), (6), for each wavelet scale (frequency band) taking advantage of the fact that the MODWT is an approximate band-pass filter with pass-bands 1/2^j + 1 < |f| ≤ 1/2^j. If the periodic boundary condition is used, the boundary coefficients (shown in red, column II) need to be discounted in order to obtain an unbiased estimate of the df, thus resulting a reduction in the df available at each scale (as described in Eq. (6)). The number of boundary coefficients at each scale is dependent on the wavelet filter used (see Eq. (4)); here we used the Daubechies L = 8 wavelet. (B) Spatial df maps for each wavelet scale (j), in a randomly selected subject, after the voxel-wise df had been estimated as in panel A, column I.