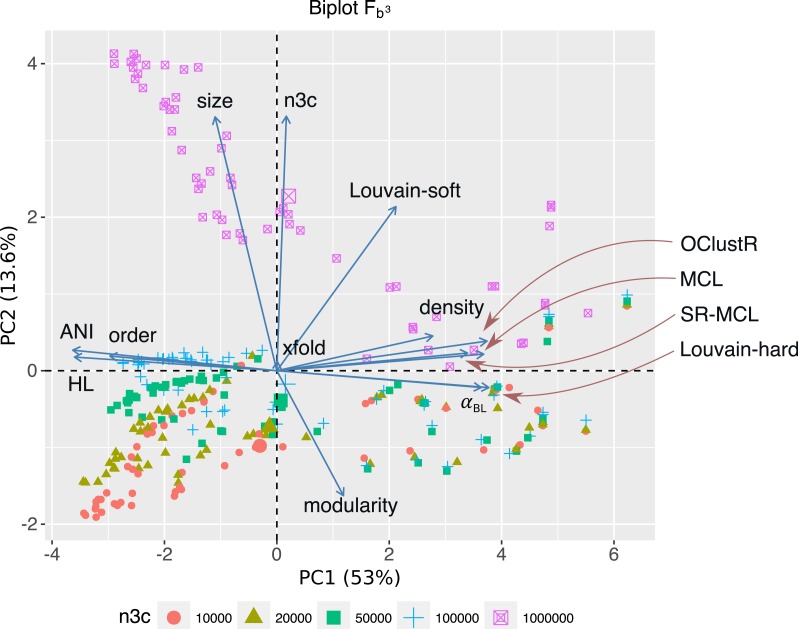
Figure 5. For the 300 3C-contig graphs pertaining to uniform abundance, a PCA biplot is shown for the two most significant components (PC1, PC2).

Respectively, PC1 and PC2 explain 53% and 13.6% of the variation within the data-set. Here vectors represent sweep variables, while points represent individual 3C-contigs graphs and are coloured by 3C sequencing depth (n3c: 10k–1M pairs). Double-sized points show mean values of these n3c groupings. Vectors labelled after the five clustering algorithms represent performance as measured by scoring metric F_B³ (Eq. 1). PC1 and PC2 explained 53% and 13.6% of the variation within the data-set respectively. PC1 was most strongly correlated with graphical complexity (H_L) and the number of graph nodes (order), which come about with decreasing evolutionary divergence (ANI_b and α_BL) and explained the majority of variation in performance for four out of five clustering algorithms. The notable exception was Louvain-soft which had significant support on PC2. PC2 was related to HiC/3C sampling depth (n3c), which correlated strongly with the number of graph edges (size). The positive response Louvain-soft had to increasing the number of HiC/3C read-pairs (n3c) relative to the remaining four algorithms is evident.