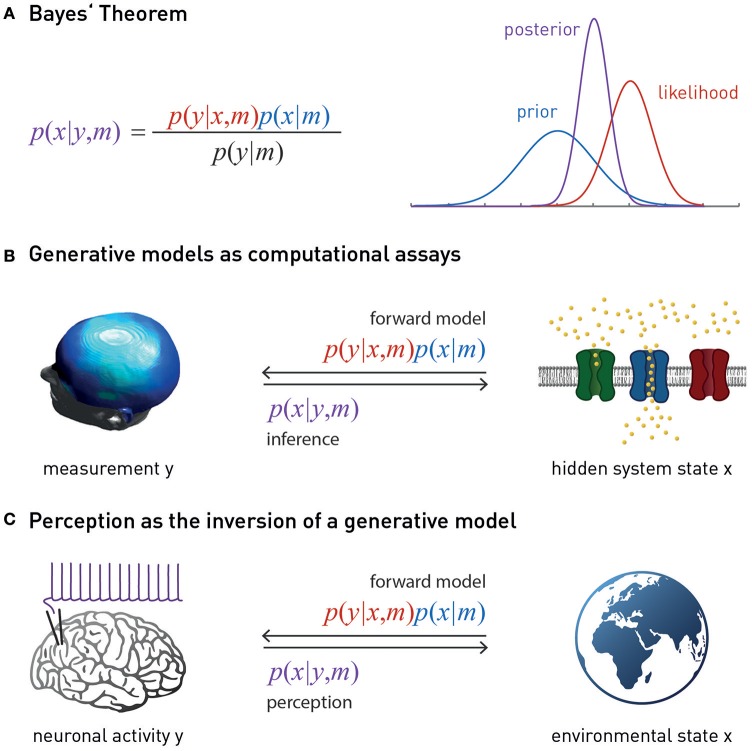
Figure 1.

(A) Bayes theorem provides the foundation for a generative model m. This combines the likelihood function p(y | x, m) (a probabilistic mapping from hidden states of the world, x, to sensory inputs y) with the prior p(x | m) (an a priori probability distribution of the world's states). Model inversion corresponds to computing the posterior p(x | y, m), i.e., the probability of the hidden states, given the observed data y. The posterior is a “compromise” between likelihood and prior, weighted by their relative precisions. The model evidence p(y | m) in the denominator of Bayes' theorem is a normalization constant that forms the basis for Bayesian model comparison—see main text. (B) Suitably specified and validated generative models with mechanistic (e.g., physiological or algorithmic) interpretability could be used as a computational assay for diagnostic purposes. The left graphics is reproduced, with permission, from Garrido et al. (2008). (C) Contemporary models of perception (the “Bayesian brain hypothesis”) assume that the brain instantiates a generative model of its sensory inputs. Perception corresponds to inverting this model, yielding posterior beliefs about the causes of sensory inputs. The globe picture is freely available from http://www.vectortemplates.com/raster-globes.php.