Time-resolved energy transfer in DNA sequence detection using water-soluble conjugated polymers: The role of electrostatic and hydrophobic interactions

Abstract

We have investigated the energy transfer processes in DNA sequence detection by using cationic conjugated polymers and peptide nucleic acid (PNA) probes with ultrafast pump-dump-emission spectroscopy. Pump-dump-emission spectroscopy provides femtosecond temporal resolution and high sensitivity and avoids interference from the solvent response. The energy transfer from donor (the conjugated polymer) to acceptor (a fluorescent molecule attached to a PNA terminus) has been time resolved. The results indicate that both electrostatic and hydrophobic interactions contribute to the formation of cationic conjugated polymers/PNA-C/DNA complexes. The two interactions result in two different binding conformations. This picture is supported by the average donor–acceptor separations as estimated from time-resolved and steady-state measurements. Electrostatic interactions dominate at low concentrations and in mixed solvents.

Conjugated polymers are novel materials with useful optical and electronic properties (1). Although structural disorder causes the effective localization length (conjugation length) to be significantly shorter than the actual chain length, an excitation can migrate along the chain before it is quenched via electron transfer to a nearby quencher (2–5) or before the excitation energy is transferred to a nearby acceptor (6–10). Thus, conjugated polymers function as light-harvesting materials and thereby exhibit greatly enhanced quenching efficiencies via electron transfer (2–5) and optical amplification via Förster resonance energy transfer (FRET) (6–10). Because of these exceptional properties, conjugated polymers offer potential for use in detecting biological and chemical target molecules with high sensitivity (2, 7–10).

To develop homogenenous biosensors, water solubility is essential. Water-soluble conjugated polymers (conjugated polyelectrolytes) are obtained by terminating the solubilizing side groups of traditional conjugated chains, e.g., poly(phenylene vinylenes) or polyfluorenes, with charged moieties (8, 9, 11, 12). Positively charged (cationic) conjugated polymers (CCPs) are particularly useful because biopolymers such as DNA and RNA are negatively charged. When these negatively charged biopolymers are labeled with fluorescent molecules, electrostatic interactions bring the fluorescent labels sufficiently close to the CCP to enable fast and efficient FRET.

The long-range excitation energy transfer from donor to acceptor via the dipole–dipole interaction was initially described by Förster (6). The rate of energy transfer for donor and acceptor separated by a distance r_DA is given by (13):

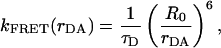where

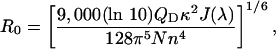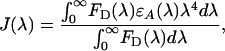τ_D is the lifetime of donor in the absence of acceptor, Q_D is the quantum yield of the donor in the absence of acceptor, N is Avogadro's number, n is the refractive index of the medium (typically assumed to be 1.4 for biomolecules in aqueous solution), and κ² is a factor describing the relative orientation of the transition dipoles of the donor and acceptor. The integral, J(λ), expresses the degree of spectral overlap between the emission of the donor, F_D(λ), and the absorption of the acceptor, ε_A(λ). R₀ is referred to as the Förster distance.

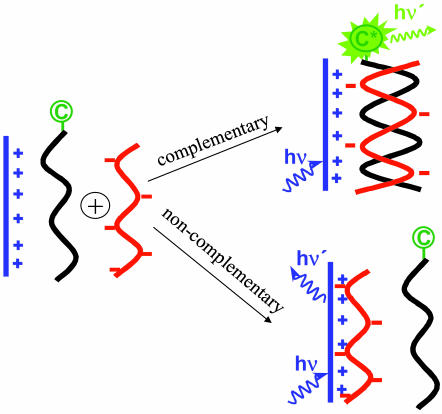
The recent demonstration of DNA sequence detection using water-soluble conjugated polymers and peptide nucleic acid (PNA) probes opened a new direction for biosensor research (9). In PNA (14, 15), the negatively charged sugar phosphate backbone of DNA is replaced by a neutral pepto-mimetic backbone, while keeping the spacing between the nucleotide bases unchanged. Thus, PNA and DNA can form duplexes similar to double-stranded DNA. Because PNA is neutral, the interaction between PNA and DNA can be used in detecting targeted DNA sequences based on the illustration shown in Scheme 1 (9).

Scheme 1.

Schematic representation for the use of a CCP with a PNA-C probe to detect the sequence of ssDNA.

The detection scheme begins with a solution that contains a CCP (as FRET donor, shown in blue) and a PNA strand (as FRET acceptor, shown in black) labeled with a fluorescent chromophate (C). The optical properties of the CCP and the fluorescent dye are chosen to satisfy the spectral requirements for efficient FRET from donor to acceptor. The concentrations are chosen so that in the initial dilute solution, the average donor–acceptor distance is too large for efficient FRET. Single-stranded DNA (ssDNA, shown in red) is then added and an appropriate annealing protocol is followed. When complementary ssDNA is added, it hybridizes with the PNA to form a negatively charged double helix. Electrostatic interactions cause the formation of a complex comprising a positively charged CCP and a negatively charged PNA-C/DNA duplex in close proximity, thereby enabling efficient FRET from the CCP to C. When noncomplementary ssDNA is added, hybridization and subsequent complex formation do not occur. As a result, with noncomplementary ssDNA, the donor–acceptor distance in the dilute solution remains too large for FRET. The PNA/ssDNA hybridization is therefore detected by enhanced emission from the acceptor. The overall scheme serves as a probe for the presence of specific targeted ssDNA sequences.

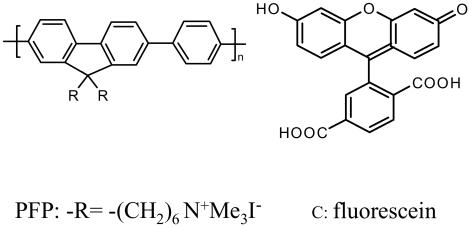
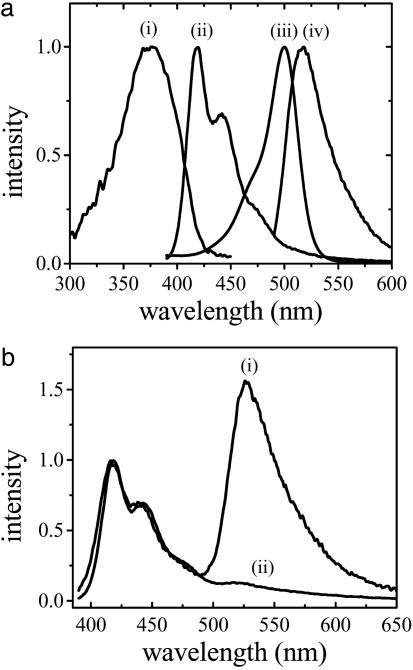
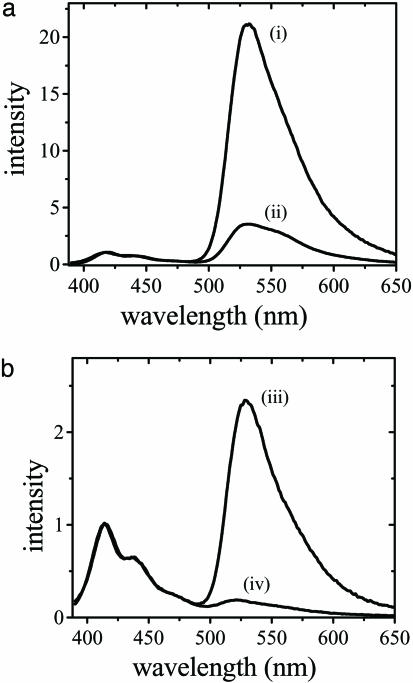
Scheme 1 was initially proposed and successfully demonstrated by Gaylord et al. (9) using poly(9,9-bis(6′-N,N,N-trimethylammonium)-hexyl)-fluorene phenylene) (PFP) with iodide counteranions (Scheme 2). The overlap between the emission of PFP (donor) and the absorption of fluorescein (C, acceptor) (Fig. 1a) ensures efficient FRET. The fluorescence spectra of the PFP/PNA-C/DNA complexes demonstrated excellent selectivity between complementary and noncomplementary PNA/DNA pairs (Fig. 1b). Furthermore, the fluorescein emission is up to 25 times more intense than that obtained from direct excitation of fluorescein at its absorption maxima in the absence of PFP. The increased fluorescein emission (optical amplification) in the energy transfer complex provides enhanced sensitivity. In the initial experiments, specific targeted sequences of DNA were detected at concentrations as low as 10 pM (9).

Scheme 2.

Molecular structures of the CCP (PFP) and fluorescein (C).

Fig. 1.

Steady-state spectra for the FRET donor, acceptor, and donor/acceptor complexes. (a) Absorption (i for PFP and iii for fluoresecin) and emission (ii for PFP and iv for fluorescein) spectra of CCP and fluorescein, respectively. (b) Emission spectra of PFP/PNA-C/DNA complex for complementary (i) and noncomplementary (ii) PNA/DNA pairs by excitation of the polymer PFP. [PFP] = 2.3 × 10^–7 M (in terms of polymer repeat units) for emission spectra in b.

Time-Resolved FRET Measurements

Studies of energy transfer dynamics can provide insight into the donor–acceptor separation and the influence of the environment on the process by which the PFP/PNA-C/DNA complex forms. PNA is known to display hydrophobic interactions, leading to aggregation at high concentrations (14). Thus, the process in Scheme 1 must be carried out at very low concentrations (<1 × 10^–5 M).

The very dilute concentrations used for the sequence-specific detection experiments are typically below the sensitivity of conventional pump–probe experiments. Additionally, pumpprobe signals from very dilute solutions are easily contaminated by the solvent response. Although conventional time-correlated single-photon counting measurements can deliver solvent response free dynamics at low concentrations, the temporal resolution is usually limited to ≈50 ps (13).

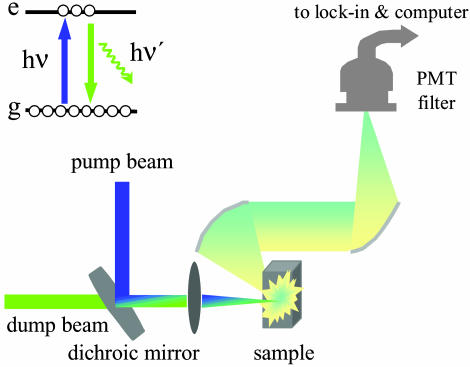
We have used ultrafast pump-dump-emission spectroscopy (PDES, as shown in Fig. 2) to time-resolve the FRET process. This technique has been used to investigate the excited-state decay dynamics and the charge generation mechanism in conjugated polymers (16–18). It also has the capability of delivering very good signal-to-noise ratio. Thus, PDES is ideal for measurements designed to time-resolve the energy transfer dynamics in the very dilute solutions required in our experiments. The laser system used in the experiments has been described (19). The 400-nm pump beam is obtained from the second harmonic of the 800-nm pulse from a regenerative amplifier. The tunable output from optical parametric amplifer (OPA) (from UV to near IR) was used for the dump beam in the experiments described here. Both pump and dump beams are intense laser beams; their relative intensities can be adjusted to optimize signal to noise (20).

Fig. 2.

Experimental arrangement for ultrafast PDES.

In PDES, the pump pulse first promotes a fraction of chromophore molecules into their excited state. The time-delayed beam then dumps the excited-state population by stimulated emission. The resulting excited-state population change is monitored via emission in the perpendicular direction, which is detected by a photomultiplier tube that is connected to a lock-in amplifier and computer system. As a result, the signal (dI/I) is negative because the dump beam decreases the excited-state population and thereby decreases the measured fluorescence. In this work, the data are presented as –dI/I for a straightforward description of the evolution of the excited-state population.

The pump and dump beams were aligned colinearly to take advantage of the long sample path length in the cuvette. This scheme for measuring the FRET dynamics in dilute solution is superior to the conventional pump/probe experiment because it detects only the fluorescence orthogonal to the pump/dump beam directions and is thus free of any contamination from solvent response, a problem that is particularly serious in very dilute solutions. In our PDES measurements, the signal-to-noise is >20 times better than that of pump-probe experiments under similar experimental conditions.

Results of the PDES Experiments

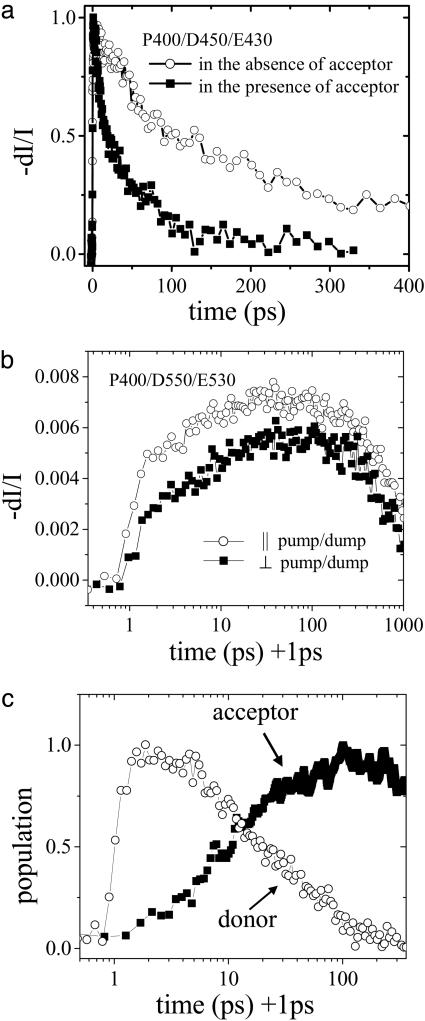
The excited-state dynamics of PFP (donor) in the absence and presence of a PNA/DNA duplex containing a fluorescein (acceptor)-labeled PNA in buffered water solution (potassium phosphate-sodium hydroxide buffer solution, 0.03 M, pH 7.4) were measured by PDES. The PDES was performed with a pump wavelength of 400 nm, a dump wavelength of 450 nm, and an emission wavelength of 430 nm. In PDES, to measure excited-state dynamics both dump and emission wavelengths need be within the donor (PFP) fluorescence spectrum. The emitted light is collected at a different wavelength from the dump beam to reduce any contamination from scattering of the dump beam.

The results of a set of PDES experiments are plotted in Fig. 3a. As expected, the donor excited-state lifetime is greatly reduced in the presence of the energy acceptor as a result of efficient FRET. In the absence of the acceptor, the PFP emission displays an initial gradual growth with a time constant of 38 ps, followed by a single exponential decay with a time constant of 400 ps. The initial signal growth arises from the Stokes shift due to solvent reorganization, geometric relaxation, and exciton migration from segments with shorter conjugation lengths to segments with longer conjugation lengths (21, 22). The exponential decay time constant (400 ps) is the fluorescence lifetime of PFP. In the presence of the acceptor, the PFP emission decay is not a single exponential; the data can be approximately fit with a double exponential with time constants of 11.5 ps (49%) and 85 ps (51%); the average lifetime is 49 ps.

Fig. 3.

Ultrafast PDES measurements on PFP/PNA-C/DNA with complementary PNA/DNA pair in buffered water solution (potassium phosphate—sodium hydroxide buffer solution, 0.03 M, pH 7.4). [PFP] = 4 × 10^–6 M (in repeat units) and [C] = 2 × 10^–7 M. (a) The excited-state decay of donor (PFP) in the absence (○) and presence (▪) of acceptor (PNA-C/DNA) measured at P400 nm/D450 nm/E430 nm. (b) The PDES data for PFP/PNA-C/DNA at P400 nm/D550 nm/E530 nm with parallel (○) and perpendicular (▪) pump/dump beam polarization. (c) The excited-state dynamics of donor (○, the P400 nm/D450 nm/E430 nm data) and acceptor (▪, obtained by subtracting donor contamination from the P400 nm/D550 nm/E530 nm data, as described in the text) for PFP/PNA-C/DNA complexes.

The excited-state dynamics of the acceptor were also monitored by PDES with a pump wavelength of 400 nm, a dump wavelength of 550 nm, and an emission wavelength of 530 nm; the results are plotted in Fig. 3b. With parallel polarized pump and dump beams, the signal rises almost instantly and gradually increases as a result of energy transfer, followed by a slow decay with a time constant of ≈2 ns, the fluorescein luminescence lifetime. The measured fluorescein lifetime is consistent with that reported (23), although there is significant uncertainty in the fitting result because of the limited time window in our measurements.

The gradual rise of the acceptor emission as a result of energy transfer can be clearly seen in the P400/D550/E530 PDES data in Fig. 3b, although there is some contamination from the donor contribution to the signal, as manifested by the initial instantaneous rise of the signal. There are several reasons for such contamination. First, the PFP donor emission has a tail that extends out to 550 nm. Even though its steady-state contribution (time integrated) is much smaller than that of the acceptor emission, its initial amplitude cannot be ignored considering the very large difference in their average lifetimes (49 ps vs. 1–3 ns), e.g., 1% contamination of the PFP emission in steady-state measurement will result in comparable amplitudes in the time-resolved measurement. Second, transient absorption measurements of polyfluorene indicate that excited-state absorption overcomes the stimulated emission at wavelengths >510 nm (24, 25). Thus, the conjugated polymer can also be promoted to an even higher energy excited state by the second beam (“dump” beam, although its role now is to further pump the excited-state population to an even higher excited state rather than to dump to the ground state). If this higher-energy excited-state population does not directly return to the first excited state (emissive state) with unity yield, e.g., it may dissociate into charge-separated pairs (16–18, 24, 25) or directly decay to the ground state in a nonradiative manner. These modulations of the excited-state population of the donor will result in the modulation of the acceptors' excited-state population and their corresponding emission intensity. These effects thus also contribute to the PDES signal at these wavelengths. On the other hand, direct excitation of the fluorescein at 400 nm is negligible because there is little absorption at this wavelength. Thus, we can safely conclude that the time-resolved acceptor emission is caused by energy transfer from PFP to fluorescein, instead of from direct excitation of fluorescein.

Considering the fact that absorption and emission transition dipole moments of the conjugated polymers are along the polymer chain, the polymer emission is locally polarized (however not fully polarized because of the homogenous nature of solution). In contrast, the fluorescein emission via energy transfer from PFP will be partially depolarized due to the inhomogenous distribution of the local fluorescin orientation with respect to the polymer chain. Thus, the beam polarization can be used to minimize the relative contribution from the conjugated polymer. As shown in Fig. 3b, when a dump beam is used with polarization perpendicular to that of the pump beam, the initial instantaneous rise caused by the polymer contamination is suppressed and the gradual increase of the acceptor emission via energy transfer is more clearly seen. Note that the depolarization here results from the population transfer via FRET. The reorientation of the entire complex (on the time scale of a few ns) and the restricted motion of the fluorescein molecules attached to the PNA terminus (on the time scale of ≈220 ps) are much slower than the energy transfer process. Consequently, the depolarization caused by these effects is negligible (unpublished work).

The net acceptor contribution (growth and subsequent decay) can be obtained by further subtracting the donor contamination as shown in Fig. 3c. As noted, the PDES signal for the P400/D550/D530 data in Fig. 3b is a superposition of both donor and acceptor contributions. The donor contribution was measured (the P400/D450/E430 data in Fig. 3a). Assuming the signal at time 0 is totally from donor contamination, the acceptor contribution was obtained by subtracting the rescaled P400/D450/E430 data (by matching the signal levels of the two data sets at time 0) from the P400/D550/D530 data in Fig. 3b. Data obtained with any polarization combination gave identical results, here the depolarized data, i.e., I_| + 2I_⊥, is used to obtain the data presented in Fig. 3c.

The energy transfer process from PFP to fluorescein in aqueous solution is very efficient, and the decay is biexponential. However, when a noncomplementary ssDNA is used under the identical conditions, the steady-state fluorescence measurements also indicate efficient energy transfer from PFP to fluorescein (Fig. 4a), implying very limited selectivity between the complementary and noncomplementary ssDNA. Thus, although the electrostatic attraction is important for complex formation, at relatively high concentrations, hydrophobic interactions also contribute significantly to bringing the polymer and fluorescein-labeled PNA in close proximity (10, 26). Hydrophobic interactions are insensitive to whether complementary or noncomplementary ssDNA are used (10).

Fig. 4.

Solvent dependence of the selectivity of the complementary and noncomplementary PNA/DNA pairs. (a) Emission spectra of PFP/PNA-C/DNA complex for complementary (i) and noncomplementary (ii) PNA/DNA pairs by excitation of the polymer PFP in water solvent. (b) Emission spectra of PFP/PNA-C/DNA complex for complementary (iii) and noncomplementary (iv) PNA/DNA pairs by excitation of the polymer PFP in water/NMP (9:1) mixed solvent. The concentrations of PFP, PNA-C, and DNA were diluted to half compared to those in a.

Macromolecules such as PNA and conjugated polymers are known to display hydrophobic interactions (11, 14). The organic core of the conjugated polymer is only partially shielded by the hydrophilic side groups. Thus, reduction of the hydrophobic interactions is necessary to improve the selectivity at high PNA and DNA concentrations. When the solution is diluted or when a fraction of organic solvent, such as N-methyl-pyrolidone (NMP) is added, the energy transfer efficiency for the non-complementary PNA/DNA pair is greatly reduced. This improved selectivity is shown in Fig. 4b. When H₂O/NMP (9:1) mixed solvent is used (where [PFP], [PNA-C], and [DNA] are reduced by half compared to Fig. 4a), there are two effects: (i) Energy transfer becomes less efficient. (ii) The selectivity between the complementary and noncomplementary PNA/DNA pairs is greatly improved.

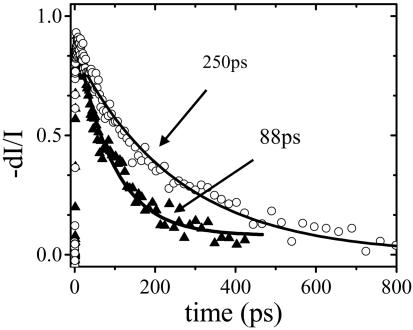
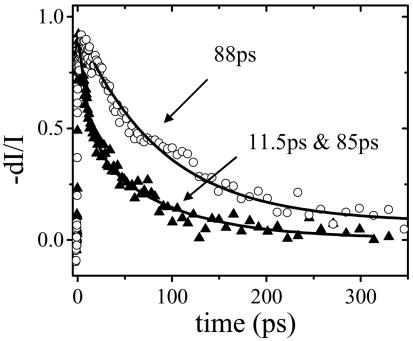
With the mixed solvent, the overall selectivity is nearly as good as obtained at very low concentrations (compare Figs. 4b and 1b). Under these conditions, PDES measurements of the donor (PFP) emission decay (Fig. 5) indicate a decay time of 88 ps for the complementary PNA/DNA pair and an energy transfer rate of 9 × 10⁹ s^–1 (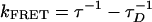, where τ and τ_D = 400 ps are the donor excited-state lifetimes in the presence and absence of acceptor, respectively). In contrast, the donor emission decays with a time constant of 250 ps for the noncomplementary PNA/DNA pair, indicating an energy transfer rate of 1.5 × 10⁹ s^–1, significantly slower than that for the complementary case. The time-resolved result is consistent with less efficient energy transfer for the noncomplementary PNA/DNA as implied by the steady-state fluorescence measurements.

Fig. 5.

The excited-state decay of PFP measured by PDES at P400 nm/D450 nm/E430 nm for PFP/PNA-C/DNA in water/NMP (9:1) mixed solvent for complementary (▴) and noncomplementary (○) PNA/DNA pairs. The solid lines are fitting results, as described in the text.

Using the spectral data in Fig. 1, the Förster distance is calculated to be 37.2 Å; Q_D = 0.37 for PFP in water is used in the calculation, and κ² = 2/3 was assumed (isotropic average) (13). The isotropic average approximation (κ² = 2/3) gives an uncertainty of ±10% in calculating donor–acceptor separations, compared to that for immobilized donor and wobbling acceptor with cone orientation of 60°, which is probably a better model for our system (27).

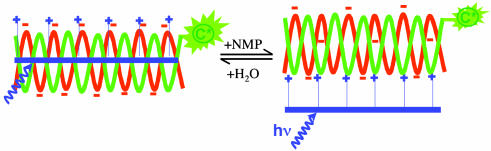
The biexponential energy transfer dynamics in water and improved selectivity by using water/organic mixed solvents indicate that both electrostatic and hydrophobic interactions contribute to the formation of polymer/PNA/DNA complexes. These two interactions result in an equilibrium between two different binding conformations as shown schematically in Scheme 3 (10). In water, the complex favors the conformation in which the positive and negative charges are exposed to the water (Scheme 3 Left). In this conformation, both electrostatic and hydrophobic interactions contribute to bringing PFP and DNA/PNA-C together. The PNA-C and PFP are closer to one another (Scheme 3 Left) than in the mixed solvent conformation (Scheme 3 Right); hence the faster component of the energy transfer process. Addition of organic solvent (NMP) reduces the hydrophobic interactions and favors the conformation sketched on Scheme 3 Right with a larger separation between PFP and PNA-C (10).

Scheme 3.

Schematic representation of the conformation equilibrium for the PFP/PNA-C/DNA complexes in water and water/NMP mixed solvents. The complex is bound by a combination of electrostatic and hydrophobic interactions in water (Left) and is only bound by electrostatic attraction in mixed solvent(Right).

This picture is supported by the average separations between CCP and fluorescein, as estimated from steady-state and time-resolved measurements (Fig. 6 and Table 1). Using R₀ = 37.2 Å, the biexponential decay in the 100% water solvent gives an energy transfer rate of 8 × 10¹⁰ s^–1 and 9 × 10⁹ s^–1 (again obtained from 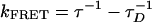with τ_D = 400 ps), corresponding to donor–acceptor separations of ≈21 and ≈30 Å. Similarly, the single exponential decay in water/NMP (9:1) mixed solvents (88 ps) corresponds to a donor–acceptor separation of ≈30 Å. Note that it might not be rigorously accurate to apply Föster theory to calculate the donor–acceptor separation for the fast component (12 ps and ≈21 Å), because the donor has not been totally relaxed (relaxation time of ≈38 ps). Its emission spectrum is not exactly known and the steady-state spectrum (fully relaxed) is used in our calculations. Nevertheless, the existence of two conformations with donor–acceptor separations of ≈21 and ≈30 Å is clearly demonstrated.

Fig. 6.

The solvent-dependent energy transfer dynamics. The excited-state decay of PFP was measured by PDES at P400 nm/D450 nm/E430 nm for PFP/PNA-C/DNA with complementary PNA/DNA pair in water (▴) and water/NMP (9:1) mixed solvent (○). The solid lines are fitting results, as described in the text.

Table 1. Decay time constants, energy transfer rates, and donor/acceptor separations in two different solvents.

Solvent	100% H2O	H2O/NMP (9:1)
Decay time constant, τ	11.5 and 85 ps	88 ps
Energy transfer rate, kFRET*	8 × 1010 s-1 and 9 × 109 s-1	9 × 109 s-1
Donor/acceptor separation, rDA	21 and 30 Å	30 Å

^*Obtained from k_FRET = τ^-1 - τ_D^-1 with τ_D = 400 ps.

The obtained donor–acceptor separations are consistent with the two conformations sketched in Scheme 3. Note, however, that these specific forms of the two different complexes (one bound by the electrostatic interaction and the other bound by a combination of hydrophobic and electrostatic interactions) are obviously only schematic representations. The actual structures remain unknown.

Summary

In this work, we have investigated energy transfer processes in DNA sequence detection by using CCPs and PNA probes with ultrafast PDES. The PDES technique provides femtosecond resolution and avoids interference from the solvent response, the latter being particularly important for studies carried out with very dilute solutions. We have used PDES to time-resolve the energy transfer from the conjugated polymer (PFP) to fluorescein, a fluorescent molecule attached to a PNA terminus.

At moderately high concentrations, the energy transfer dynamics from PFP to fluorescein is biexponential in aqueous solution, with poor selectivity between the complementary and noncomplementary PNA/DNA. The selectivity can be improved by using mixed water/organic solvents, although the energy transfer becomes less efficient. The results indicate that both electrostatic and hydrophobic interactions can cause the formation of CCP/PNA-C/DNA complexes. The two interactions result in the equilibrium between two different binding conformations sketched in Scheme 3. This picture is supported by the average separations between CCP and fluorescein as estimated from steady-state and time-resolved measurements.