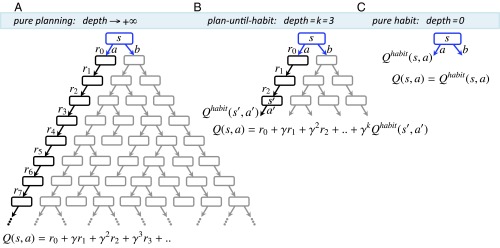
Fig. 1.

Schematic of the algorithm in an example decision problem (see SI Appendix for the general formal algorithm). Assume an individual has a “mental model” of the reward and transition consequent on taking each action at each state in the environment. The value of taking action $a$ at the current state $s$ is denoted by $Q(s,a)$ and is defined as the sum of rewards (temporally discounted by a factor of $0\le \gamma \le 1$ per step) that are expected to be received upon performing that action. $Q(s,a)$ can be estimated in different ways. (A) “Planning” involves simulating the tree of future states and actions to arbitrary depths ($k\to \infty )$ and summing up all of the expected discounted consequences, given a behavioral policy. (B) An intermediate form of control (i.e., plan-until-habit) involves limited-depth forward simulations ($k=3$ in our example) to foresee the expected consequences of actions up to that depth (i.e., up to state $s\text{'}$). The sum of those foreseen consequences ($r_0+\gamma r_1+{\gamma }^2{r}_2$) is then added to the cached habitual assessment [${\gamma }^k{Q}_{habit}(s\text{'},a\text{'})$] of the consequences of the remaining choices starting from the deepest explicitly foreseen states ($s\text{'}$). (C) At the other end of the depth-of-planning spectrum, “habitual control” avoids planning ($k=0$) by relying instead on estimates $Q_{habit}(s,a)$ that are cached from previous experience. These cached values are updated based on rewards obtained when making a choice.