Estimating relative risk of a log-transformed exposure measured in pools

Abstract

Pooling biospecimens prior to performing laboratory assays is a useful tool to reduce costs, achieve minimum volume requirements, and mitigate assay measurement error. When estimating the risk of a continuous, pooled exposure on a binary outcome, specialized statistical techniques are required. Current methods include a regression calibration approach, where the expectation of the individual-level exposure is calculated by adjusting the observed pooled measurement with additional covariate data. While this method employs a linear regression calibration model, we propose an alternative model that can accommodate log-linear relationships between the exposure and predictive covariates. The proposed model permits direct estimation of the relative risk associated with a log-transformation of an exposure measured in pools.

1. Introduction

In epidemiological studies, pooling biospecimens prior to performing laboratory assays can help reduce lab costs, lessens assay measurement error in the observations, and achieve minimum volume requirements by combining only a small portion of each sample into a larger pool [1–5]. Pooling is currently used to screen blood for diseases such as HIV [6–10], biomonitor prevalence of environmental exposures [11, 12], and reduce measurement error in genetic microarray studies [13].

When analyzing pooled specimens in a regression setting, specialized statistical techniques are often needed. If the pooled samples are to be included as a predictor of a binary outcome, a set-based logistic regression model yields unbiased estimates when pools are matched on case status [5], or in matched survival studies [14]. If pools are not matched on the outcome, more complex methods may be required [15, 16]. This scenario could occur, for instance, if pools are formed and assayed before the outcome of interest is observed [15]. In such cases, Zhang and Albert [15] proposed a regression calibration (RC) approach to perform regression of a binary outcome on a pooled predictor. Regression calibration is typically applied in measurement error problems; in the pooling scenario, a pooled measurement is treated as a mis-measured value of each of the individual concentrations of the specimens comprising that pool. The existing regression calibration approach for pools uses ancillary information to adjust the observed measurement of the pooled sample, by estimating the linear relationship between the pooled variable and potential predictors. This method performs well when the pooled biomarker is approximately normally distributed.

If individual values of the biomarker are available (i.e. no pooling is performed), a regression model on a log-transformation of the exposure may be of interest, particularly when a biomarker is positive and right-skewed [17, 18]. When measured in pools, a log-transformation on the pooled measurements can induce computational complexity, due to the non-linearity of the log function. In light of recent developments for regression on a log-transformed, pooled outcome [19, 20], we propose an extension of the pooled regression calibration approach that will permit estimation of regression coefficients corresponding to a log-transformed biomarker, when only pooled measurements are available.

In Section 2, we set up the regression model and summarize the existing regression calibration method for an untransformed biomarker. In the following section we describe our proposed methods for extending this regression calibration approach to a log-transformed predictor variable that is logarithmically associated with the auxiliary predictive covariates. We then use simulation studies to compare the performance of the proposed approaches to existing methods in estimating relative risk, and we apply these strategies using data from the Effects of Aspirin in Gestation and Reproduction (EAGeR) trial to determine the association between prenatal serum leptin levels and the outcome of live birth.

2. Regression Calibration: Untransformed Predictor

In this section, we summarize the methods presented by Zhang and Albert [15] to apply a regression calibration approach to an untransformed exposure. While these methods were originally developed for a general link function, we specifically focus on the log link, to investigate the common scenario when the relative risk is of primary interest. Thus, for all of the methods that follow, we assume we are interested in estimating the relative risk associated with a biomarker of interest that is measured in pools. When all N specimens are measured individually, the relative risk associated with the untransformed exposure is commonly estimated under the model:

$$Pr(Y_i=1\mid X_i,{\mathbf{C}}_i)=E(Y_i\mid X_i,{\mathbf{C}}_i)=exp(\alpha +\beta X_i+{\mathit{\gamma }}^{\prime }{\mathbf{C}}_i)$$ (1)

for i = 1, …, N, where Y_i is the binary outcome, X_i the exposure of interest that is only observed after laboratory analysis, C_i a vector of observed covariates, γ a vector of regression coefficients, and exp(β) is the relative risk associated with a 1-unit increase in X. Model (1) is commonly fit parametrically assuming that Y follows a binomial or Poisson distribution, often employing a sandwich estimator for robust standard error estimation [21, 22].

When the exposure is measured in pools instead of on individual specimens, the pooled measurement ${\overline{X}}_i=g_i^{-1}{\sum }_{j=1}^{g_i}{X}_{ij}$ is observed, assumed to be the average of the concentrations of specimens comprising that pool [23], where g_i is the number of specimens in pool i, (i = 1, …, n), n denotes the total number of pools, and ${\sum }_{i=1}^n{g}_i=N$.

Zhang and Albert [15] showed that, through application of a first-order Taylor Series approximation, X̄_i could be related to the outcome approximately by:

$$Pr(Y_{ij}=1\mid {\overline{X}}_i,{\mathbf{C}}_{ij})\approx exp\{\alpha +\beta E(X_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})+{\mathit{\gamma }}^{\prime }{\mathbf{C}}_{ij}\}$$

where the ‘ij’ subscript denotes the j^th subject in the i^th pool. $E(X_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})$ is the expected value of the individual specimen concentration, given the observed measurement of pool i as well as additional covariate information { ${\mathbf{C}}_{ij}^{\ast }:j=1,\dots ,g_i$}, which consists of the individual-level vector of covariates for each individual in pool i({C_ij}), as well as potentially additional auxiliary variables. The quality of this Taylor Series approximation depends on the higher-order (2nd and higher) centered moments of the distribution $f(X_{ij}\mid {\overline{X}}_i,{\mathbf{C}}_{ij}^{\ast })$, where the approximation works best when these values are small [15].

Under the linear regression calibration approach, a linear relationship between X_ij and ${\mathbf{C}}_{ij}^{\ast }$ is assumed, such that

$$X_{ij}={\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }+{\epsilon }_{ij}$$ (2)

where the ε_ij’s are assumed to be independent and identically-distributed with E(ε_ij) = 0 and Var(ε_ij) = σ² for all j = 1, …, g_i, i = 1, …, n. It follows that:

$${\overline{X}}_i={\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\overline{\mathbf{C}}}_i^{\ast }+{\epsilon }_i$$ (3)

where $E({\epsilon }_i)=g_i^{-1}{\sum }_{j}E({\epsilon }_{ij})=0$ and $\mathit{Var}({\epsilon }_i)=g_i^{-2}{\sum }_j\mathit{Var}({\epsilon }_{ij})=g_i^{-1}{\sigma }^2$. ${\overline{\mathbf{C}}}_i^{\ast }$ is a matrix of covariates, where each column represents the average across the individual-level covariate values within pool i (i.e. ${\overline{\mathbf{C}}}_i^{\ast }=g_i^{-1}{\sum }_{j=1}^{g_i}{\mathbf{C}}_{ij}^{\ast }$).

By combining equations (2) and (3), $E(X_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})$ can then be derived as follows:

$$\begin{array}{l}{X}_{ij}=({\overline{X}}_i-{\overline{X}}_i)+{\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }+{\epsilon }_{ij}\\ ={\overline{X}}_i-({\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\overline{\mathbf{C}}}_i^{\ast }+{\epsilon }_i)+({\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }+{\epsilon }_{ij})\\ ={\overline{X}}_i+{\mathit{\varphi }}_1^{\prime }({\mathbf{C}}_{ij}^{\ast }-{\overline{\mathbf{C}}}_i^{\ast })+{\eta }_{ij}\end{array}$$ (4)

where E(η_ij) = E(ε_ij) − E(ε_i) = 0 and thus

$$E(X_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})={\overline{X}}_i+{\mathit{\varphi }}_1^{\prime }({\mathbf{C}}_{ij}^{\ast }-{\overline{\mathbf{C}}}_i^{\ast })={\overline{X}}_i+E(X_{ij}\mid {\mathbf{C}}_{ij}^{\ast })-E({\overline{X}}_i\mid {\overline{\mathbf{C}}}_i^{\ast }).$$

Although the individual X’s are unobserved, ϕ̂ = (ϕ̂₀, ϕ̂₁) can be estimated by a weighted least squares on the pooled measurements [24]. Similar to the traditional regression calibration approach for measurement error, $E(X_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})$ acts as an adjustment on X̄_i, the observed ‘mis-measured’ value of X_ij, given the information inherent in { ${\mathbf{C}}_{ij}^{\ast }$}. The estimated relative risk, exp(β̂), can then be obtained by substituting $\widehat{E}(X_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})={\overline{X}}_i+{\widehat{\mathit{\varphi }}}_1^{\prime }({\mathbf{C}}_{ij}^{\ast }-{\overline{\mathbf{C}}}_i^{\ast })$ for X_ij in equation (1) and following with standard binomial or Poisson regression.

3. Regression Calibration: Log-transformed predictor

While the linear regression calibration approach described in Section 2 estimates the risk associated with an untransformed exposure, it is often of interest to estimate the risk based on a log-transformation of the exposure, particularly when that predictor is highly skewed. In this scenario, the regression model based on the individual-level data is:

$$Pr(Y_{ij}=1\mid X_{ij},{\mathbf{C}}_{ij})=exp\{\alpha +\beta (log{X}_{ij})+{\mathit{\gamma }}^{\prime }{\mathbf{C}}_{ij}\}.$$ (5)

Here, exp(β) represents the risk associated with a 1-unit increase in log(X). To fit this regression model when X is measured in pools, we again employ a Taylor Series expansion, where

$$Pr(Y_{ij}=1\mid {\overline{X}}_i,{\mathbf{C}}_{ij})\approx exp\{\alpha +\beta E(log{X}_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})+{\mathit{\gamma }}^{\prime }{\mathbf{C}}_{ij}\}.$$ (6)

To facilitate calibration of the log-transformed individual biomarker values, we propose two alternative methods to directly estimate $E(log{X}_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})$, which are particularly suited for capturing logarithmic relationships between the individual-level exposure and the covariates. First, we exploit the convenient summation properties of the gamma distribution to employ a parametric strategy, which will theoretically obtain maximum precision when the distributional assumptions are correctly specified. Next, we consider an alternative estimation procedure based on recently-developed quasi-likelihood methods for pooled measurements. This method is expected to be more flexible in accommodating alternate distributional assumptions, as it requires specification of the first two moments, as opposed to the full distribution, of the exposure conditional on the remaining covariates.

3.1. Parametric Calibration

Similar to the log-normal distribution, the gamma distribution can effectively characterize positive, right-skewed random variables. In addition, the convenient summation properties of the gamma distribution make it particularly amenable to analyzing biomarker data measured in pools [3, 23, 25, 26]. In this section, we exploit these convenient properties to obtain a closed form expression for $E(log{X}_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})$.

Suppose that ( $X_{ij}\mid {\mathbf{C}}_{ij}^{\ast }$) follows a gamma distribution with shape k_ij and scale θ, where $log{k}_{ij}={\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }$ and $E(X_{ij}\mid {\mathbf{C}}_{ij}^{\ast })=k_{ij}\theta =\theta exp({\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast })$. Letting S_i = g_iX̄_i denote the sum of the individual specimens comprising pool i, it follows directly from the summation property of the gamma distribution that $S_i\mid \{{\mathbf{C}}_{ij}^{\ast }\}~\mathit{Gamma}({\sum }_j{k}_{ij},\theta )$ and $(S_i-X_{ij})\mid \{{\mathbf{C}}_{ij}^{\ast }\}~\mathit{Gamma}({\sum }_{j^{\prime }\ne j}{k}_{i{j}^{\prime }},\theta )$. Then (X_ij/S_i|S_i, { ${\mathbf{C}}_{ij}^{\ast }$}) follows a beta distribution, since:

$$\begin{array}{l}f(X_{ij}\mid S_i,{\mathbf{C}}_{ij}^{\ast })=\frac{f(X_{ij},S_i\mid {\mathbf{C}}_{ij}^{\ast })}{f(S_i\mid {\mathbf{C}}_{ij}^{\ast })}\\ =\frac{f(X_{ij}\mid {\mathbf{C}}_{ij}^{\ast })f(S_i-X_{ij}\mid {\mathbf{C}}_{ij}^{\ast })}{f(S_i\mid {\mathbf{C}}_{ij}^{\ast })}\\ =\frac{\mathrm{\Gamma }({\sum }_j{k}_{ij})}{\mathrm{\Gamma }(k_{ij})\mathrm{\Gamma }({\sum }_{j^{\prime }\ne j}{k}_{i{j}^{\prime }})}\frac{X_{ij}^{k_{ij}-1}{(S_i-X_{ij})}^{({\sum }_{j^{\prime }\ne j}{k}_{i{j}^{\prime }}-1)}}{S_i^{{\sum }_j{k}_{ij}-1}}\\ =\frac{\mathrm{\Gamma }({\sum }_j{k}_{ij})}{S_i\mathrm{\Gamma }(k_{ij})\mathrm{\Gamma }({\sum }_{j^{\prime }\ne j}{k}_{i{j}^{\prime }})}{\left(\frac{X_{ij}}{S_i}\right)}^{(k_{ij}-1)}{\left(1-\frac{X_{ij}}{S_i}\right)}^{({\sum }_{j^{\prime }\ne j}{k}_{i{j}^{\prime }}-1)}.\end{array}$$

By applying a transformation of variables, we see that $(X_{ij}/S_i\mid S_i,\{{\mathbf{C}}_{ij}^{\ast }\})~\mathit{Beta}(k_{ij},{\sum }_{j^{\prime }\ne j}{k}_{i{j}^{\prime }})$.

We can then use the properties of the beta distribution to derive the conditional expectation of the individual concentrations given the measured average (or equivalently, the measured sum) of the pool as well as additional individual-level auxiliary variables:

$$\begin{array}{l}E(log{X}_{ij}\mid S_i,\{{\mathbf{C}}_{ij}^{\ast }\})=log(S_i)+E\left[log\left(\frac{X_{ij}}{S_i}\right)\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\}\right]\\ =log(S_i)+\psi (k_{ij})-\psi \left(\sum _j{k}_{ij}\right)\\ =log(S_i)+E(log{X}_{ij}\mid {\mathbf{C}}_{ij}^{\ast })-E(log{S}_i\mid \{{\mathbf{C}}_{ij}^{\ast }\})\end{array}$$

where ψ is the digamma function [27] and the final step follows from the properties of the gamma distribution. Hence, similar to its linear analogue, the regression calibration step assuming a gamma distribution on X|C^* involves adjusting the observed ‘mis-measured’ value log X̄_i with ancillary information based on the relationship between X and C^*. To obtain the calibrated value of log X_ij for each individual specimen, ${\widehat{k}}_{ij}=exp({\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast })$ is estimated for all i, j by optimizing the log-likelihood of the gamma distribution with constant scale parameter [20]. Calculation of $E(log{X}_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})$ is then straightforward. Once obtained, this value is plugged into the regression model (6). Example R code to obtain the maximum likelihood estimates from this gamma calibration approach is provided in the Appendix.

3.2. Quasi-Likelihood Calibration

While the parametric assumption on ( $X_{ij}\mid {\mathbf{C}}_{ij}^{\ast }$) will theoretically provide the most precise estimates of ϕ̂ when correctly specified, a less restrictive approach may be preferred if ( $X_{ij}\mid {\mathbf{C}}_{ij}^{\ast }$) does not follow a gamma distribution. For this method, we assume a linear relationship between log X_ij and ${\mathbf{C}}_{ij}^{\ast }$, such that:

$$log{X}_{ij}={\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }+{\epsilon }_{ij}$$ (7)

where E(ε_ij) = 0 and Var(ε_ij) = σ². Then, similar to the approach outlined in equation (4), we can re-write this expression as:

$$\begin{array}{l}log{X}_{ij}=(log{\overline{X}}_i-log{\overline{X}}_i)+{\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }+{\epsilon }_{ij}\\ =log{\overline{X}}_i-log\left\{g_i^{-1}\sum _{j}exp({\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }+{\epsilon }_{ij})\right\}+{\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }+{\epsilon }_{ij}\\ =log{g}_i{\overline{X}}_i-log\left\{\sum _{j}exp({\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }+{\epsilon }_{ij})\right\}+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }+{\epsilon }_{ij}.\end{array}$$

Applying a first-order Taylor Series approximation to the second log function, the conditional expectation is then:

$$\begin{array}{l}E(log{X}_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})\approx log{g}_i{\overline{X}}_i-log\left\{\sum _{j}exp({\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast })E(e^{{\epsilon }_{ij}})\right\}+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }\\ =log{g}_i{\overline{X}}_i-logE(e^{{\epsilon }_{11}})-log\left\{\sum _{j}exp({\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast })\right\}+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast }\end{array}$$

which follows directly from the assumption that the ε_ij’s are identically distributed. Estimates of ϕ₁ are found using an extension of the quasi-likelihood method for pools [19]. Under equation (7), $E({\overline{X}}_i\mid \{{\mathbf{C}}_{ij}^{\ast }\})=g^{-1}{\sum }_{j}exp({\varphi }_0^{\ast }+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast })$, where ${\varphi }_0^{\ast }={\varphi }_0+logE\{exp({\epsilon }_{11})\}$, and $\mathit{Var}({\overline{X}}_i\mid \{{\mathbf{C}}_{ij}^{\ast }\})=\nu g^{-2}{\sum }_{j}exp\{2({\varphi }_0^{\ast }+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast })\}$, where ν = Var{exp(ε₁₁)}/E{exp(ε₁₁)}². Then the following quasi-score function is solved:

$$\sum _{i=1}^n\frac{{\overline{X}}_i-{\mu }_i}{V_i(\mathit{\varphi })}\frac{d{\mu }_i}{d\mathit{\varphi }}=0$$

where ${\mu }_i=g_i^{-1}{\sum }_{j}exp({\varphi }_0^{\ast }+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast })$ and $V_i(\mathit{\varphi })=g_i^{-2}{\sum }_{j}exp({\varphi }_0^{\ast }+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast })$. Note that ν is omitted from the function V_i since it does not affect estimation of the parameters of interest, ϕ. Normally, ν would be absorbed into the estimate of the dispersion parameter. However, since we only seek to identify a point estimate for $E(log{X}_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})$, a function of ϕ₁, estimation of the dispersion parameter is unnecessary for our purposes. Furthermore, since ${\varphi }_0^{\ast }$ is a function of E{exp(ε₁₁)}, its estimator will not be an unbiased estimate of ϕ₀. However, since the main value of interest does not depend on ϕ₀, it is also treated as a nuisance parameter. After obtaining estimates of ϕ̂₁ from the quasi-score function, $\widehat{E}(log{X}_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})$ is substituted into (6). Since $E(X_{ij}\mid {\mathbf{C}}_{ij}^{\ast })=E(e^{{\epsilon }_{11}})exp({\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast })$ and $E({\overline{X}}_i\mid \{{\mathbf{C}}_{ij}^{\ast }\})=g^{-1}E(e^{{\epsilon }_{11}}){\sum }_{j}exp({\varphi }_0+{\mathit{\varphi }}_1^{\prime }{\mathbf{C}}_{ij}^{\ast })$, we can write:

$$\begin{array}{l}E(log{X}_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})\approx {\alpha }^{\ast }+log{\overline{X}}_i+logE(X_{ij}\mid {\mathbf{C}}_{ij}^{\ast })-logE({\overline{X}}_i\mid \{{\mathbf{C}}_{ij}^{\ast }\})\\ ={\alpha }^{\ast }+log\left\{{\overline{X}}_i\frac{E(X_{ij}\mid {\mathbf{C}}_{ij}^{\ast })}{E({\overline{X}}_i\mid \{{\mathbf{C}}_{ij}^{\ast }\})}\right\}\end{array}$$ (8)

where α^* = −log E(e^ε₁₁). Thus, similar to the regression calibration goal of adjusting a mis-measured value based on auxiliary information, this approximation adjusts the ‘mis-measured’ value of X̄_i multiplicatively based on the additional information of the expected value of the individual-level biomarker concentration (X_ij) given the individual-level observed covariates ( ${\mathbf{C}}_{ij}^{\ast }$). Furthermore, adding a constant (e.g. α^*) to the approximation of $E(log{X}_{ij}\mid {\overline{X}}_i,\{{\mathbf{C}}_{ij}^{\ast }\})$ will not change the estimate of β or γ in (6), since this constant will be absorbed into the intercept term. Thus, it is unnecessary to estimate the value of log E(e^ε₁₁), and this term can also be treated as a nuisance parameter. Example code for each of these methods is provided in the Appendix.

4. Simulation Study

In this section we perform simulations to test the performance of each of these methods in estimating the relative risk of a log-transformed, pooled predictor on a binary outcome. 5000 simulations of 1000 observations were performed for various pool sizes to mimic the motivating study from the EAGeR trial, described in more detail in Section 6. Two confounders, C₁ and C₂, were generated to resemble Age and BMI, respectively. C₁ was generated from a truncated normal distribution with a mean of 28 and standard deviation of 3.5, and with lower and upper limits of 18 and 42, to reflect the age distribution of the population of women in the EAGeR trial, specifically, pre-menopausal women attempting pregnancy. C₂ was generated from a log-normal distribution with a geometric mean of E(log C₂|C₁) = 3.2 + 0.002(C₁) and geometric variance of 0.05. To test these methods under various distributions of X|C, separate simulation studies were run, with X|C generated under a gamma distribution, a log-normal distribution, and a normal distribution.

For the first set of simulations, the exposure of interest was generated under a gamma distribution with scale parameter θ = 300 and:

$$E(X\mid C_1,C_2)=exp\{-1-0.02C_1+3.2log{C}_2\}.$$

These parameters were chosen to mimic the distribution of leptin in the EAGeR study, as described in more detail in Section 6. Under this simulation, the parametric approach from Section 3.1 is correctly specified. Furthermore, the assumptions on the first and second moments of E(X|C₁, C₂) that are needed for the quasi-likelihood approach in (8) are satisfied when X|C is generated under a gamma distribution. Thus, the quasi-likelihood calibration procedure is also correctly-specified in this scenario.

For the second set of simulations, X was generated under a log-normal distribution with geometric standard deviation of 0.25 such that:

$$E(logX\mid C_1,C_2)=-1.5-0.02C_1+3.2log{C}_2.$$

This distribution corresponds to the assumption of a linear association between log X and C, as in Section 3.2. Thus, the multiplicative adjustment to the pooled measurement using quasi-likelihood estimates of ϕ are correctly-specified in this scenario, while the assumption of the conditional gamma distribution needed for the parametric calibration method is misspecified. Results from this model will help illuminate potential consequences of misspecification of the distribution of X|C under the parametric regression calibration approach.

A skewed exposure distribution does not necessarily imply that a log-linear or gamma regression calibration model will provide the best predicted values of the individual-level X’s. Rather, the aptness of a log-linear or gamma model to predict individual-level exposure values depends more on the underlying link function than the skewness of the distribution [28]. For instance, if a covariate C is highly skewed, while X|C is normally-distributed, the marginal distribution of X may be skewed, even though a linear link function would more accurately capture the relationship between X and C. The advantage of the proposed regression calibration models is the ability to capture a logarithmic relationship between the exposure and some predictive covariates. Since the goal in fitting the calibration model is to ‘adjust’ the pooled values of the exposure back to the individual-level values, the model that most appropriately characterizes the relationship between X and C is preferred. Thus, we also conducted simulations where X|C is normally-distributed, in which case the linear regression calibration described in Section 2 would provide the best predictions of the individual-level X’s; expected values are incorporated into the outcome model as in Equation (8). In this scenario, X is generated with mean:

$$E(X\mid C_1,C_2)=-100-0.02C_1+3.2C_2^2$$

and a standard deviation of 40. This model differs from the previous simulations since X is dependent on $C_2^2$, rather than log C₂, to generate a skewed marginal distribution for X while retaining an underlying linear link function.

After simulating the exposure of interest, the outcome Y for each simulation study was then generated under a binomial distribution with log link such that:

$$E(Y\mid X,C_1,C_2)=exp\{0.8-0.1logX-0.015C_1-0.01C_2^{\ast }\}$$

where $C_2^{\ast }=I(C_2\ge 25)$ is a binary variable designed to mimic an indication of whether a participant is overweight, where C₂ represents BMI. The regression coefficients were chosen to emulate those observed in the EAGeR data analysis, where Y represents the outcome of live birth. Note that C₂ and $C_2^{\ast }$ are highly correlated, and C₂ can be considered an auxiliary variable useful in helping predict the individual-level values of X. After generating the simulated data, pools with an equal number of specimens were artificially formed to have size 2, 4, and 8, to assess the potential impact of higher pool sizes on parameter estimation.

Models were fit under the complete data (“Full”), the naive model (“Naive”), the existing linear regression calibration approach (“Linear RC”), a regression calibration assuming a gamma distribution on X|C (“Gamma RC”), and a regression calibration approach assuming a log-linear relationship between X and C and estimating the corresponding parameters using quasi-likelihood (“Log-linear RC”). All models were fit assuming a linear relationship between Y and the log-transformed individual-level X’s. Poisson models with robust variance were fit according to (6), where the calibrated value for $E(log{X}_{ij}\mid {\overline{X}}_i,{\mathbf{C}}_{ij}^{\ast })$ differed according to the assumptions underlying the relationship between X and C.

The full model, fit on the complete data, is considered the gold standard, since this is the model that would be available if all individual specimen concentrations were measured, assuming no measurement error. The naive model simply substitutes the pooled values for the individual X’s in (5), which is essentially equivalent to a linear regression calibration approach with no covariates (i.e. an intercept-only model). The linear regression calibration model assumes a linear relationship between X and C to obtain an estimate of the expected value of the individual level concentrations, given the observed covariates and pooled values, ${\widehat{X}}_{ij}=\widehat{E}(X_{ij}\mid {\mathbf{C}}_{ij}^{\ast },{\overline{X}}_i)$. To fit this model, this calibrated value was substituted for X in (5).While this ad hoc substitution and log-transformation does not conform to the original proposed methods of Zhang and Albert [15], our goal in fitting this model was to determine the extent to which an inappropriate application of the regression calibration approach may result in invalid inference. Correct application of the regression calibration approach as described in Section 2 has been shown to provide unbiased and efficient estimates of β when only pooled measurements are available, and the goal is to estimate the risk associated with an untransformed exposure [15]. In addition, we demonstrate the utility of this method when X|C is normally-distributed in the third simulation scenario. Furthermore, while Zhang and Albert [15] tested several versions of the regression calibration approach, including imputation vs. augmentation, and a plug-in vs. normal distribution assumption, we only apply regression calibration under the imputation approach (as described in Section 2) and normal distribution assumption on X|C, since this method performed best, in general, in the simulation scenarios presented by Zhang and Albert [15]. In addition, while the Y_ij’s corresponding to the same pool are generally correlated with each other given X̄_i, we fit regression models under the correlation structure of working independence, since additional testing of alternate structures did not noticeably improve estimation of the parameters of interest or their standard errors [15].

In addition to fitting the full, naive, and linear regression calibration models, we also apply the regression calibration approach assuming a gamma distribution for X|C. Under the first simulation scenario, this model is correctly specified, so estimates of β should be consistent. While this approach is not correctly-specified under the second simulation study when X|C is generated from a log-normal distribution, the gamma distribution can adequately characterize skewed distributions in epidemiological studies [29–31].

Estimation of the maximum likelihood estimates ϕ̂ under the gamma assumption was conducted using the optim function in R. To improve convergence, several starting values were tested. Finally, the regression calibration assuming a linear relationship between log X and C was fit, where R’s nleqslv function was applied to solve the non-linear system of quasi-likelihood estimating equations (see Appendix for details).

5. Simulation Results

Tables 1 and 2 provide the percent bias, empirical standard deviation, average estimated standard error, and 95% confidence interval coverage for β when X|C is generated under a gamma and lognormal distribution, respectively. Based on these simulation results, both the gamma and log-linear RC models give approximately unbiased estimates of the β coefficients with nominal 95% confidence interval coverage, when the true conditional exposure distribution is log-normal or gamma. These results hold regardless of pool size. Furthermore, the precision of these estimates under these proposed models is close to the full precision under the complete model, even for pools of size 8, when the total number of lab assays is reduced from 1000 to 125. This precision is likely a reflection of the predictive capacity of the model due to the high correlation between the simulated covariates and the exposure of interest.

Table 1.

Simulation results when X|C is generated under a gamma distribution. Relative bias, empirical standard deviation (SD), and average estimated standard error ( $\widehat{\text{SE}}$) are multiplied by 100 to facilitate comparison between methods.

Pool Size	Method	β1 = −0.1				γ1 = −0.015				γ2 = −0.01
		Bias x 100	SD x 100	$\widehat{\text{SE}}$ x100	95% CI Coverage	Bias x 100	SD x 100	$\widehat{\text{SE}}$ x 100	95% CI Coverage	Bias x 100	SD x 100	$\widehat{\text{SE}}$ x 100	95% CI Coverage
2	Full	−0.05	4.83	5.01	96.0	−0.02	0.74	0.75	95.5	0.03	7.75	7.85	95.5
	Naive	4.71	5.19	5.37	85.8	0.12	0.73	0.74	95.3	−8.83	5.92	5.99	69.1
	Linear RC	5.19	3.83	4.00	75.9	0.05	0.77	0.78	95.7	−5.07	7.05	7.08	89.1
	Gamma RC	−0.37	5.55	5.59	95.3	−0.02	0.74	0.75	95.4	0.10	8.23	8.24	95.2
	Log-Linear RC	−0.37	5.55	5.59	95.3	−0.02	0.74	0.75	95.5	0.11	8.23	8.24	95.2
4	Full	−0.05	4.83	5.01	96.0	−0.02	0.74	0.75	95.5	0.03	7.75	7.85	95.5
	Naive	5.61	6.75	6.83	86.8	0.15	0.73	0.74	95.1	−10.6	5.45	5.47	50.8
	Linear RC	5.44	3.92	4.13	75.7	0.06	0.78	0.79	95.4	−5.48	7.01	7.03	88.0
	Gamma RC	−0.43	5.78	5.80	95.0	−0.02	0.74	0.75	95.4	0.12	8.43	8.40	95.5
	Log-Linear RC	−0.44	5.78	5.80	94.9	−0.02	0.74	0.75	95.3	0.14	8.43	8.41	95.4
8	Full	−0.05	4.83	5.01	96.0	−0.02	0.74	0.75	95.5	0.03	7.75	7.85	95.5
	Naive	5.94	9.17	9.22	90.6	0.16	0.73	0.74	95.1	−11.3	5.27	5.29	42.6
	Linear RC	5.45	4.02	4.24	77.7	0.06	0.78	0.79	95.6	−5.54	6.98	7.05	87.7
	Gamma RC	−0.44	5.87	5.88	95.1	−0.02	0.74	0.75	95.3	0.14	8.52	8.48	95.1
	Log-Linear RC	−0.45	5.87	5.88	95.1	−0.02	0.74	0.75	95.2	0.14	8.52	8.49	95.1

Table 2.

Simulation results when X|C is generated under a log-normal distribution. Relative bias, empirical standard deviation (SD), and average estimated standard error ( $\widehat{\text{SE}}$) are multiplied by 100 to facilitate comparison between methods.

Pool Size	Method	β1 = −0.1				γ1 = −0.015				γ2 = −0.01
		Bias x 100	SD x 100	$\widehat{\text{SE}}$ x100	95% CI Coverage	Bias x 100	SD x 100	$\widehat{\text{SE}}$ x 100	95% CI Coverage	Bias x 100	SD x 100	$\widehat{\text{SE}}$ x 100	95% CI Coverage
2	Full	−0.01	4.74	4.84	95.5	0.00	0.69	0.70	95.2	0.04	7.30	7.36	95.3
	Naive	4.73	4.86	4.96	84.2	0.13	0.68	0.70	94.8	−8.46	5.60	5.59	67.6
	Linear RC	5.52	3.45	3.67	68.8	0.08	0.72	0.73	95.3	−5.16	6.43	6.59	88.4
	Gamma RC	0.26	5.09	5.14	95.2	0.00	0.69	0.70	95.2	−0.41	7.56	7.57	95.4
	Log-linear RC	0.32	5.06	5.11	95.1	0.00	0.69	0.70	95.3	−0.33	7.59	7.60	95.4
4	Full	−0.01	4.74	4.84	95.5	0.00	0.69	0.70	95.2	0.04	7.30	7.36	95.3
	Naive	5.68	6.11	6.22	85.1	0.15	0.68	0.70	94.8	−10.3	5.18	5.13	48.5
	Linear RC	5.74	3.62	3.84	69.5	0.08	0.73	0.74	95.4	−5.50	6.45	6.58	87.0
	Gamma RC	0.21	5.31	5.35	95.2	0.00	0.69	0.71	95.0	−0.32	7.77	7.76	94.9
	Log-linear RC	0.28	5.27	5.31	95.2	0.00	0.69	0.71	95.0	−0.28	7.78	7.78	95.0
8	Full	−0.01	4.74	4.84	95.5	0.00	0.69	0.70	95.2	0.04	7.30	7.36	95.3
	Naive	5.95	8.30	8.34	88.8	0.16	0.68	0.70	94.6	−10.9	5.00	4.97	40.9
	Linear RC	5.71	3.76	3.96	71.8	0.08	0.73	0.75	95.1	−5.50	6.50	6.62	87.5
	Gamma RC	0.21	5.46	5.42	94.4	0.00	0.69	0.71	94.9	0.10	8.95	8.07	94.8
	Log-linear RC	0.17	5.38	5.44	95.3	0.00	0.69	0.71	95.0	−0.14	7.94	7.90	94.9

On the other hand, regression coefficient estimates from the naive and linear regression calibration models (‘Linear RC’) are biased under the first two simulation scenarios. Although this bias is not excessive (~5 to 10% bias), the artificially low precision of these estimates results in sub-nominal 95% confidence interval coverage, despite accurate estimation of standard errors. These coverage rates, which drop below 70% for the linear regression calibration model and under 41% for the naive model, make these methods particularly susceptible to inflated Type I Error rates due to misspecification of the calibration model.

When the exposure is linearly related to the covariates, however, the linear regression calibration model performs best, with approximately unbiased coefficients, nominal 95% confidence interval coverage, and the lowest standard errors among the calibrated models (Table 3). Although the log-linear and gamma regression calibration models are misspecified, they continue to provide approximately unbiased coefficient estimates with close to nominal confidence interval coverage, demonstrating robustness to misspecification of the link function. Estimates under the naive model, on the other hand, remain biased, similar to those from the previous simulation scenarios, which subsequently corresponds to sub-nominal confidence interval coverage rates.

Table 3.

Simulation results when X|C is generated under a normal distribution. Relative bias, empirical standard deviation (SD), and average estimated standard error ( $\widehat{\text{SE}}$) are multiplied by 100 to facilitate comparison between methods.

Pool Size	Method	β1 = −0.1				γ1 = −0.015				γ2 = −0.01
		Bias x 100	SD x 100	$\widehat{\text{SE}}$ x100	95% CI Coverage	Bias x 100	SD x 100	$\widehat{\text{SE}}$ x 100	95% CI Coverage	Bias x 100	SD x 100	$\widehat{\text{SE}}$ x 100	95% CI Coverage
2	Full	0.07	7.42	7.55	95.4	0.00	0.62	0.63	95.7	−0.05	7.27	7.19	95.0
	Naive	4.94	7.57	7.63	89.4	−0.01	0.62	0.63	95.6	−5.68	5.25	5.20	79.8
	Linear RC	0.07	7.44	7.57	95.5	0.00	0.62	0.63	95.7	−0.05	7.28	7.20	94.8
	Gamma RC	0.34	7.58	7.56	95.1	0.00	0.62	0.63	95.7	−0.35	7.43	7.17	94.2
	Log-Linear RC	−0.21	7.75	7.80	95.3	0.00	0.62	0.63	95.6	0.08	7.39	7.28	94.8
4	Full	0.07	7.42	7.55	95.4	0.00	0.62	0.63	95.7	−0.05	7.27	7.19	95.0
	Naive	5.80	9.73	9.68	90.3	−0.01	0.62	0.63	95.6	−6.79	4.76	4.70	69.1
	Linear RC	0.06	7.46	7.58	95.4	0.00	0.62	0.63	95.7	−0.05	7.29	7.20	94.7
	Gamma RC	0.18	7.82	7.69	94.7	0.01	0.63	0.63	95.5	−0.11	7.86	7.39	93.3
	Log-Linear RC	−0.43	7.97	7.98	94.9	0.00	0.62	0.63	95.6	0.17	7.46	7.35	94.6
8	Full	0.07	7.42	7.55	95.4	0.00	0.62	0.63	95.7	−0.05	7.27	7.19	95.0
	Naive	6.03	13.18	13.14	92.4	−0.01	0.62	0.63	95.5	−7.20	4.56	4.52	64.2
	Linear RC	0.06	7.46	7.58	95.3	0.00	0.62	0.63	95.6	−0.04	7.29	7.20	94.7
	Gamma RC	−0.16	7.96	7.84	94.7	0.01	0.63	0.63	95.3	0.11	7.96	7.43	93.7
	Log-Linear RC	−0.57	8.10	8.09	94.8	0.00	0.62	0.63	95.6	0.23	7.50	7.38	94.6

As mentioned previously and demonstrated in the simulation studies, the choice of calibration model is not dictated by the skewness of the marginal distribution of X. While the gamma and log-linear calibration models demonstrated robustness to misspecification in the final simulation study, the ability to choose the best model could improve estimate efficiency. While several methods exist for comparing model fit, the difficulty arises in the flexibility of these models to accommodate pooled, i.e. averaged, X values. Thus, in this scenario, we choose to use the root mean squared error (RMSE) to compare relative goodness of fit of the calibration models, due to its flexibility in assessing pooled values as well as its non-parametric underpinnings, which facilitate comparison across distributional assumptions. When applied to pooled values of X, the RMSE is defined as: $\mathit{RMSE}=\sqrt{n^{-1}{\sum }_{i=1}^n{({\overline{X}}_i-{\widehat{X}}_i)}^2}$ and ${\widehat{X}}_i=g_i^{-1}{\sum }_{j=1}^{g_i}\widehat{E}(X_{ij}\mid {\mathbf{C}}_{ij}^{\ast })$ is the predicted pooled value based on the predicted individual-level values from the calibration model. While not a formal test of goodness of fit, comparing RMSE values across the calibration models can guide selection of the preferred model, where a lower RMSE value suggests a better fit. To demonstrate this, we provide average RMSE values for the calibration models under each simulation scenario in Table 4.

Table 4.

Average root mean squared error (RMSE) for the calibration models under each simulation scenario.

Pool Size	Method	Distribution of X|C
		Gamma	Log-normal	Normal
2	Naive	5380	3546	793
	Linear RC	2665	1992	28
	Gamma RC	1161	1304	163
	Log-linear RC	1167	1311	53
4	Naive	3799	2504	560
	Linear RC	1876	1402	19
	Gamma RC	817	916	107
	Log-linear RC	821	922	31
8	Naive	2679	1765	394
	Linear RC	1314	983	13
	Gamma RC	571	645	61
	Log-linear RC	575	646	20

When X|C is generated under the gamma or log-normal models, the average RMSE for the gamma and log-linear calibration models are quite similar, but both are considerably lower than the linear calibration model, indicating that both the gamma or log-linear calibration models fit the data better than the linear model. When X|C is generated under a normal model, however, a comparison of the RMSE values clearly indicates that a linear regression calibration model provides the best fit. In addition, the RMSE values from the naive model, which is equivalent to a linear calibration model with no covariates (the intercept-only model), has the highest RMSE in all scenarios. While the naive model is not a real contender for a calibration model in this scenario, RMSE values under this model can illustrate how much the other calibration models may be improving the predicted values of the X’s. If the RMSE for each calibration model were close to that from the naive model, the calibration step would be of little benefit to improving the fit of the final outcome model. Thus, comparing RMSE values can guide selection of the best calibration model, as well as provide an indication of the extent of improvement available over the naive model.

Due to the strong similarity in performance between gamma and log-linear regression calibration models, choice of which to fit could depend on the researcher’s preference concerning the assumptions and tools required to produce maximum likelihood or quasi-likelihood estimates, especially when the RMSE values fit under these models are similar. For instance, the gamma assumption requires full specification of the parametric distribution and involves maximization of the log-likelihood. The quasi-likelihood approach, while only requiring assumptions on the mean and variance of log X|C, relies on the performance of the Taylor Series approximation. If both procedures are employed but provide contradictory results, the discrepancy might indicate a more serious violation of the underlying model assumptions on the individual-level data.

6. Data Analysis

The Effects of Aspirin in Gestation and Reproduction (EAGeR) Trial was a prospective, multi-site, double-blinded randomized controlled trial, designed to evaluate the effects of preconception low-dose aspirin on gestation among women with a prior history of pregnancy loss. Women in the study were 18–40 years old, had reported 1 or 2 prior pregnancy losses and were actively attempting to conceive. These women had no prior gynecologic disease and had not been diagnosed with infertility. Baseline characteristics were recorded and blood draws were taken at randomization. Participants were followed for up to 6 cycles of attempting pregnancy; if they became pregnant, they were followed until the end of pregnancy [32].

Leptin is a hormone that plays a significant role in human physiology and reproduction, and recent studies have demonstrated an association between leptin in menstrual function and pregnancy-related conditions [34–37]. The goal of this data analysis was to determine whether higher levels of leptin were associated with adverse pregnancy outcomes in the EAGeR trial after adjusting for potential confounders, where the outcome of interest is live birth. Due to the strong correlation between BMI and leptin [33], overweight status is considered a potential confounder of the relationship between leptin and pregnancy outcome. In this dataset, the median leptin concentration among normal weight women (BMI < 25) was 9.0 ng/mL, while the median concentration among overweight women was 34.3 ng/mL. Age was also considered as a potential confounder.

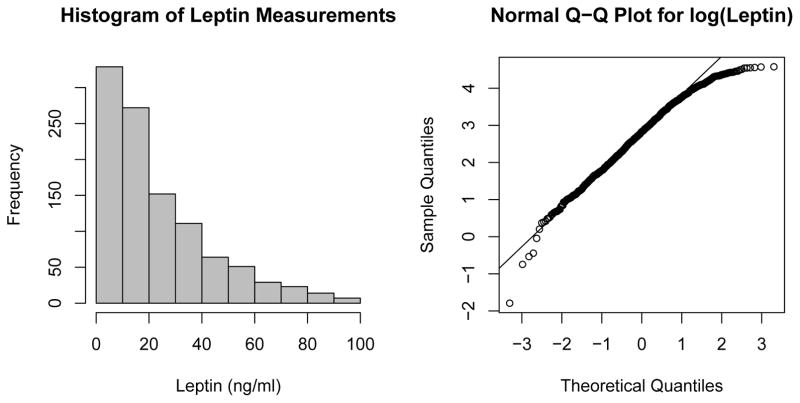
1052 observations with complete data on live birth outcome, leptin measurements, age, and BMI were available for analysis. Leptin concentration was measured for women at baseline using the Quantikine ELISA assay (R&D Systems, Minneapolis, MN), and BMI and age were assessed from the baseline questionnaire. The distribution of leptin concentration in the study sample was positive and right-skewed, with a median of 16.96 ng/mL and a mean of 23.42 ng/mL. A histogram of the individual-level concentrations as well as a normal Q-Q plot of log(leptin) are provided in Figure 1.

Figure 1.

Histogram and normal Q-Q plot of leptin and log(leptin) concentrations, respectively, measured on individual specimens obtained from participants in the EAGeR trial.

Since previous research has assessed the association between log-transformed leptin levels and health outcomes [38–45], we apply a log-transformation to leptin to estimate the relative risk associated with a 1-unit increase of leptin on the log scale. Specifically, we seek to estimate the association between leptin and birth outcome after controlling for overweight status and age, based on the following regression model:

$$E(\text{Live}\text{birth})=exp\{{\beta }_0+{\beta }_{1}log(\text{leptin})+{\gamma }_1\text{Age}+{\gamma }_2\text{Overweight}\}$$ (9)

where ‘Live birth’ is the binary outcome indicating whether a participant had a live birth, ‘Age’ is measured in years, and ‘Overweight’ is a binary variable indicating a woman categorized as overweight or obese based on pre-pregnancy BMI (BMI ≥ 25). Since leptin concentrations were measured on individual specimens, we can directly compare results from analyses on artificially pooled samples to the gold standard based on individual-level measurements. To illustrate the proposed methods, pools were artificially formed first of size 2 (n = 526), then of size 4 (n = 263). For all models, Poisson distributions with log link and robust variance were fit to directly estimate β. Continuous BMI values were applied as ancillary information to help calibrate values of log-transformed leptin for analyses when only the pooled measurements are available.

Table 5 gives parameter estimates and standard errors under the full data as well as for each of the models discussed in Sections 2 and 3 for pool sizes of 2 and 4. In addition, RMSE values for the calibration models are provided as a relative goodness of fit criterion. Under the full data based on individual measurements of leptin, log(leptin) tris significantly negatively associated with live birth at a significance level of 0.05 (Relative Risk = 0.9). Consistent with previous knowledge, age was also negatively associated with live birth, an association that was preserved under all scenarios. When leptin is measured in pools, the naive and linear regression calibration (‘Linear RC’) models underestimate the magnitude of the association detected under the full data, and are unable to detect this significant association. Of note, the linear regression calibration model suffered from additional missing data (32 observations) due to a log-transformation on negative expected values in the regression calibration step.

Table 5.

Regression coefficient estimates and standard errors when regressing live birth on log(leptin), age, and overweight status in the EAGeR study. A ‘*’ indicates a statistically significant association at the 0.05 level. RMSE refers to the root mean squared error of the calibration model.

Pool Size	Method	log(Leptin)	Age	Overweight	RMSE
1	Full Data	−0.111 (0.040)*	−0.018 (0.006)*	−0.016 (0.078)	–
2	Naive	−0.061 (0.051)	−0.017 (0.006)*	−0.124 (0.066)	13876
	Linear RC	−0.033 (0.038)	−0.018 (0.006)*	−0.109 (0.079)	7512
	Gamma RC	−0.120 (0.057)*	−0.018 (0.006)*	−0.014 (0.091)	7448
	Log-linear RC	−0.121 (0.057)*	−0.018 (0.006)*	−0.011 (0.091)	7453
4	Naive	−0.035 (0.071)	−0.017 (0.006)*	−0.152 (0.061)	9814
	Linear RC	−0.059 (0.046)	−0.019 (0.006)*	−0.080 (0.088)	5258
	Gamma RC	−0.141 (0.074)	−0.018 (0.006)*	0.011 (0.107)	5253
	Log-linear RC	−0.128 (0.069)	−0.018 (0.006)*	−0.003 (0.103)	5205

On the other hand, the regression calibration approaches assuming a gamma distribution or log-linear relationship give point estimates that are close to those under the full data. Furthermore, the standard errors of these estimates are precise enough to detect the significant association between log(leptin) and live birth with only 526 (as opposed to 1052) assays required. When pools are formed of size 4, none of the methods retain sufficient power to detect the significant association between log(leptin) and live birth. However, the gamma and log-linear RC models continue to calculate coefficient estimates that are similar to those under the full data.

The RMSE values provide a guide to choose the best calibration model in this analysis. When pool size is 2, the RMSE suggests that the gamma regression calibration model provides the best fit, with the log-linear calibration model performing similarly. In fact, these two models provide regression coefficient estimates similar to those from the full model, with the gamma model giving the closest estimates. When pool size is 4, the RMSE values suggest that the log-linear model is preferred and in fact, this model does slightly outperform the gamma and linear calibration models with respect to approximating estimates from the full data for log(leptin) and age. In real-world scenarios, when the full data is unavailable, the RMSE values can help select the best calibration model from among a set of pre-specified candidates.

This data analysis illustrates the potential benefits of applying a gamma or log-linear regression calibration approach to pooled data when the association between a log-transformed exposure and a binary outcome is of primary interest. Importantly, this analysis is for illustration purposes only and should not be interpreted as a complete and robust estimate of the association between leptin levels and live birth outcome, as this inference would require appropriate handling of additional statistical issues such as missing data, selection bias, measurement error, and other potential confounders.

7. Discussion

Pooling biospecimens prior to performing lab assays has been gaining traction as a cost-saving strategy in epidemiological studies in recent years with the development of statistical tools necessary for analysis. In this study, we have contributed to the toolkit of available analytical methods for pooled specimens by developing two new approaches to estimate relative risk when an exposure is measured in pools and the risk associated with the log-transformation of this exposure is of primary interest. We chose to focus on the logarithmic transformation of an exposure due to the popularity of this strategy in epidemiological studies. While it may be possible to extend these methods to additional monotonic transformations (e.g. square root), a thorough exploration of this topic is beyond the scope of this paper. In addition, while we only expounded upon a log link in the outcome model to specifically investigate the performance of these methods when estimating a relative risk, these methods could also be applied to general link functions, by combining the proposed calibration models for the expectation of a log-transformed exposure, with the original methodology for untransformed exposures as described in Zhang and Albert [15].

The proposed approaches were developed as an extension of an existing regression calibration method for pooled exposures, which was based on a linear adjustment to the pooled measurements, applying the measurement error approach of regression calibration to correct for the pools acting as ‘mis-measured’ values of the individual-level concentrations [15]. Since this method was not developed for a log-transformed exposure, our methods were proposed with the goal of direct calibration of the log-transformed individual-level biomarker values, particularly when the log-transformed exposure is linearly associated with the predictive covariates.

The first of the proposed methods exploited the convenient summation properties of the gamma distribution to derive a closed-form expression for the conditional expectation of the individual-level log-transformed exposures given the measured pooled values and supplementary auxiliary information. In contrast, the second approach assumes a linear relationship between the log-transformed exposure and the auxiliary variables. While the parametric methods assuming a gamma distribution should theoretically provide the most precise estimates when correctly-specified, our empirical simulations demonstrated negligible differences between the two methods. Implementation of each of these methods, however, does require different computational methods (e.g. maximizing the log-likelihood vs. solving a system of nonlinear equations), as demonstrated in the example code in the Appendix.

Since the regression calibration methods rely on a Taylor Series approximation, at least some amount of bias may be unavoidable. These methods, however, will often provide considerable improvement over the naive model with respect to estimating the regression coefficients, in which the pooled measurements are included as predictors in the regression model without any adjustment. The success of the regression calibration approach depends on the amount of relevant auxiliary variable information available, and the predictive value of these variables on the pooled exposure. If the biomarker of interest is uncorrelated with all of the auxiliary covariates, the regression calibration approach is indistinguishable from the naive method, which, as evidenced in the simulation studies, can result in bias and sub-nominal confidence interval coverage. On the other hand, a covariate that is perfectly predictive of the individual-level exposure concentrations will produce risk estimates that are equivalent to the full model. Thus, the goal of regression calibration is to shift estimates away from the biased estimates produced by the naive model, towards those from the full model. It may be difficult, however, to determine how close the adjusted estimates come to the gold standard of the individual-level data. While RMSE provides a useful tool to compare candidate calibration models, it does not provide an absolute measure of predictive capacity. Additional validation data containing measurements on individual-level exposure values may be required to assess the absolute fit of the calibration model.

Since the regression calibration approach can essentially be viewed as a single imputation approach, where observed relationships in the data are leveraged to predict expected values of the unobserved (individual-level) concentrations of the biomarker, a multiple imputation framework may improve this approach. This strategy could incorporate outcome information into the imputation procedure, and could be generalized to calibrate additional missing covariate information in the dataset. We are currently testing the feasibility of this method applied to pooled specimens.

As evidenced in the data analysis, pooling can impact the power to detect a significant association. Strategic pooling techniques, where pools are formed to be homogeneous with respect to important covariates, can help improve power when pooling is performed [4, 24]. In the data example, for instance, pooling specimens from subjects with similar BMI values could enhance prediction of the individual-level leptin values, subsequently improving precision of the regression coefficients in the outcome model. Similar methods to those presented here will still be applicable. Pooling on the outcome, however, creates additional complexities in the analysis, similar to those associated with outcome-dependent sampling [46, 47]. In a non-pooled scenario, logistic regression can accommodate outcome-dependent sampling (i.e. case-control sampling) directly, while log-linear regression requires additional adjustments such as propensity score weighting to mitigate selection bias. Similarly, when pools are formed to be homogeneous on the outcome, a set-based logistic regression model will provide unbiased regression coefficient estimates. However, it is unclear how to extend this model to accommodate a log-transformation on a pooled exposure [5]. Under log-linear regression with a pooled, log-transformed exposure, adjustments similar to propensity weighting may be necessary to counteract the bias induced by pooling on the outcome, as in the non-pooled scenario. While recent research has explored this topic in a slightly different scenario [46], additional efforts are needed to determine how a similar method could be extended to a log-transformed exposure. In summary, careful consideration of pooling design can help reduce cost, attain minimum volume requirements for lab assays, and reduce the number of measurements below the limit of detection. When appropriate analytical techniques are applied to these pooled measurements, reliable and efficient inference can be obtained.

Appendix

Example R Code: Table A1 gives the first 12 observations from the example dataset on which subsequent code is based. Example code calculates estimates for ϕ̂, then E(log X|C^*), and applies this value to the original log-linear regression model.

Table A1.

Example dataset of a binary outcome (Y), covariates (C1 and C2), and an exposure measured in pools (Pooled_X).

Y	C1	C2	Pooled_X	Pool_Number
1	0	1.818	0.549	1
0	0	2.865	0.549	1
1	0	1.319	0.549	1
1	0	2.458	0.549	1
0	0	1.538	0.575	2
0	1	2.209	0.575	2
0	0	1.757	0.575	2
0	1	1.817	0.575	2
0	0	2.359	1.096	3
0	0	1.765	1.096	3
1	1	1.750	1.096	3
0	0	1.623	1.096	3

## Data set-up:
# Calculate poolwise averages of additional covariates
     Pooled_C1 = ave(C1,Pool_Number)
     Pooled_C2 = ave(C2,Pool_Number)
# Calculate pool weights (i.e. pool size) for weighted least squares
     Pool_wts = tabulate(Pool_Number)[Pool_Number]
## Regression Calibration Step:
  # 1. Weighted Least Squares (Zhang and Albert, 2011)
         rc.ZA = glm(Pooled_X ∼ Pooled_C1+Pooled_C2,weights=Pool_wts)
         E.X = cbind(1,C1,C2)%*%rc.ZA$coef
         E.XP = ave(E.X,Pool_Number)
         ZA.Xhat = Pooled_X + E.X - E.XP
  # 2. Parametric Gamma assumption on X|C
       # Define log-likelihood for Gamma distribution:
          gamma.ll = function(theta,Pooled_X,C,pool=1:length(Pooled_X),pool.size){
              scale = theta[length(theta)] # scale parameter
              phi = theta[-length(theta)]
              mu.ij = exp(as.matrix(cbind(1,C))%*%phi)
              mu.i = ave(mu.ij,pool,FUN=sum)
              ll = sum(dgamma(Pooled_X,shape=mu.i/scale,
                            scale=scale/pool.size,log=T))
              return(-ll)
          }
          xfit.GA = optim(c(1,0,0,1),gamma.ll,Pooled_X=Pooled_X,
                                     # can try different starting values to improve convergence
                                     C=cbind(C1,C2),pool=Pool_Number,pool.size=Pool_wts)
          EX.GA = exp(cbind(1,C1,C2)%*%xfit.GA$par[1:3])
          ES.GA = ave(EX.GA,Pool_Number,FUN=sum)
          logGA.Xhat = log(Pooled_X*Pool_wts) + digamma(EX.GA) - digamma(ES.GA)
  # 3. Quasi-likelihood regression calibration
       # Define quasi-likelihood for alternate version:
          library(nleqslv)
          QL.htro = function(phi,Pooled_X,C,pool=1:length(Pooled_X),pool.size){
               mu.ij = exp(as.matrix(cbind(1,C))%*%phi)
               V.ij = mu.ijˆ2
               mu.i = ave(mu.ij,pool,FUN=mean)[!duplicated(pool)]
               V.i = (ave(V.ij,pool,FUN=sum)/pool.sizeˆ2)[!duplicated(pool)]
               dmu = apply(as.matrix(cbind(1,C))*c(mu.ij),2,ave,pool)[!duplicated(pool),]
               Q = t(dmu)%*%as.matrix((Pooled_X-mu.i)/V.i)
               return(Q)
          }
          xfit.QL = nleqslv(c(0,0,0),QL.htro, Pooled_X = Pooled_X[!duplicated(Pool_Number)],
                                       C=cbind(C1,C2),pool=Pool_Number,pool.size=Pool_wts)
          EX.QL = exp(cbind(1,C1,C2)%*%xfit.QL$x)
          EXP.QL = ave(EX.QL,Pool_Number)
          logQL.Xhat = log(Pooled_X)+log(EX.QL)-log(EXP.QL)
## Fit original regression model on calibrated X values
# Zhang and Albert (2011) version on log-transformed X:
   glm(Y∼C1+C2+log(ZA.Xhat),family=quasibinomial(link=log))
# Parametric Gamma Reg. Cal. on log(X):
   glm(Y∼C1+C2+logGA.Xhat,family=quasibinomial(link=log))
# Quasi-Likelihood Reg. Cal. on log(X):
   glm(Y∼C1+C2+logQL.Xhat,family=quasibinomial(link=log))