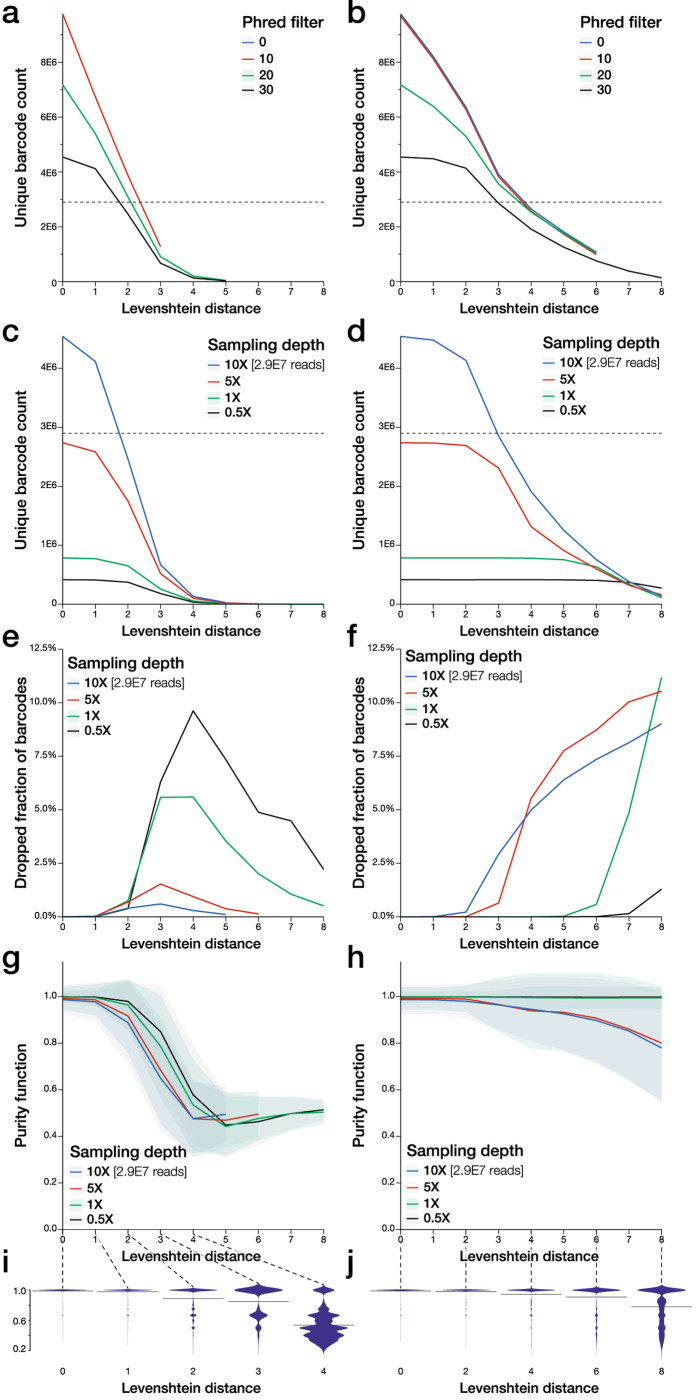
Figure 8. Validation of the Starcode message passing clustering algorithm using library 4.

(a) To determine the true identity of all unique barcodes and the real library content, we evaluated two clustering algorithms on the NextSeq sequencing data set from library 4. The NextSeq identified 9 762 153 unique barcodes although only 3 × 10⁶ clones were observed during the library preparation. The Starcode software package multi-purpose “sphere clustering” reduced the number of unique barcode sequences down to the expected number (dashed line in a–d) at a Levenshtein distance around 2. (b) The more advanced algorithm in Starcode, tailored for barcode clustering based on a variation of the Needleman–Wunsch (NW) algorithm and provides an message passing clustering. This required a Levenshtein distance of around 4 to reach the expected barcode count. Due to the non-linear increase in memory requirements with the increase in Levenshtein distance threshold of these algorithms, the calculations failed to complete at some of the highest levels with the 196 gb ram and 1 Tb SSD ram swap file we had at hand for this computation. (c,d) Both algorithms require a read depth of 10x the clone count to recover all unique barcodes as seen through subsampling of the read counts (evaluated after filtration by phred of min 30). (e,f) Both algorithms include an evaluation of ties and discards barcodes that are ambiguous at the point of clustering, i.e., at equal distance to two generated clusters. However, the sphere clustering displays an inverted U shape of the fraction of discarded barcodes while compared to the saturating rate in the message passing clustering algorithm. (g,i) However, the biggest difference between the two algorithms was observed by studying the purity function. If two, truly unique, barcodes are falsely clustered together, this would reduce the purity measurement as they would point to different fragments. While an observable reduction in barcode purity was seen already at a Levenshtein distance threshold of 2 and completely breaks down at a distance of 4, (h,k) the message passing clustering algorithm manages to retain the barcodes highly pure up to a distance of 6.