Subtraction-based approach for enhancing the depth sensitivity of time-resolved NIRS

Abstract

The aim of this study was to evaluate enhancing of the depth sensitivity of time-resolved near-infrared spectroscopy with a subtraction-based approach. Due to the complexity of light propagation in a heterogeneous media, and to prove the validity of the proposed method in a heterogeneous turbid media we conducted a broad analysis taking into account a number of parameters related to the method as well as various parameters of this media. The results of these experiments confirm that the depth sensitivity of the subtraction-based approach is better than classical approaches using continuous-wave or time-resolved methods. Furthermore, the results showed that the subtraction-based approach has a unique, selective sensitivity to a layer at a specific depth. In vivo application of the proposed method resulted in a greater magnitude of the hemodynamic changes during functional activation than with the standard approach.

1. Introduction

Accurate estimation of optical properties of heterogeneous tissue structures by near-infrared spectroscopy (NIRS) methods is challenging [1]. Perhaps nowhere is this better exemplified than using NIRS to measure the optical properties of brain tissue, which requires contending with significant signal contamination from superficial tissue layers (skull and scalp). Various techniques have been developed to overcome this problem. The most popular and widely used in brain applications is multi-distance continuous-wave (CW) NIRS [2]. This method is based on the assumption that depth sensitivity is proportional to source-detector (r_SD) separation. Consequently, signals changes that occurs in the extracerebral layers can be monitored by acquiring NIRS data with a relatively small source-detector distance (r_SD ≈1 cm), while data acquired at a larger distance (r_SD > 3 cm) will provide sensitivity to the brain. CW-NIRS is frequently used in functional NIRS (fNIRS) studies [4,5].

The most advanced NIRS method is based on the time-resolved (TR) technique, which measures the distribution of times of flight of diffusely reflected photons (DTOFs) [6,7]. Measuring the DTOF not only provides a means of separating the effects of light scatter from absorption, it also provides greater depth sensitivity since light that have only travelled through superficial layers is detected earlier than light that penetrates deeper layers [7,8]. Moment analysis is a well-established method of improving depth sensitivity and determining the optical properties from DTOFs that was first introduced by Liebert et al. [9]. The first three statistical moments of DTOFs: N – total number of photons, <t> – mean time of flight and V – variance are typically calculated. Due to the positive skewness of measured DTOFs, higher moments (<t>, V) are more sensitive to late-arriving photons. However, even these higher moments still have significant contribution from early-arriving photons [11]. Binning methods applied to DTOFs can be used to isolate photons with longer arrival times, but this approach is prone to signal-to-noise (SNR) limitations and requires careful measurement of the instrument response function (IRF) [8,12–14].

In a previous paper we presented a subtraction method (referred to as sTR) applied to the higher moments of DTOFs measured at two source-detector distances. The original objective was to avoid the need to measure the instrument response function (IRF) when measuring the absorption coefficient [15]. Moreover, it was found that the sTR method also provided more accurate estimates of the optical properties of heterogeneous media. This is not unexpected considering that higher order statistical moments and subtraction CW measurements have both been used independently to improve depth sensitivity [4,13,16,17]. The aim of the current study was to further investigate the improved depth sensitivity provided by the sTR method. Monte Carlo simulations and tissue-mimicking phantoms were used to determine how the depth sensitivity was affected by both source-detector separation and the separation between the two detectors. For comparison, moment analysis was also applied to DTOFs acquired at each detector separately [9]. As a final demonstration, TR-NIRS data acquired from the primary motor cortex during motor activation, and the magnitudes of the oxyhemoglobin concentration increases derived from moments analysis and sTR were compared.

2. Methodology

The absorption coefficient, μ_a, of a semi-infinite turbid medium can be estimated by applying moment analysis to a DTOF measured at a given source-detector separation (herein referred to as individual moment analysis or iMA) [9]:

$${\mu }_a=\frac{{<t>}^3}{2cV\left({<t>}^2+V\right)}$$ (1)

where: c refers to the speed of light in the medium. The accuracy of this approach depends on carefully measuring the instrument response function.

For the sTR method, μ_a is estimated based on the difference in the mean time of flight (∂<t>) and variance (∂V) calculated from two DTOFs measured at separate source–detector distances. As outlined in [15], μ_a can be determined by:

$${\mu }_a=\frac{\partial <t>}{2c\partial V}$$ (2)

2.1 Monte-Carlo simulations

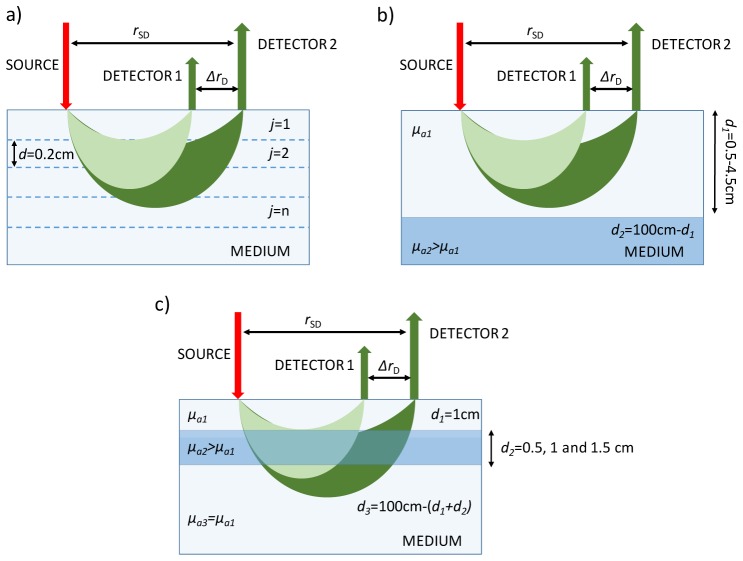
Monte Carlo (MC) simulations of heterogeneous media were conducted to assess potential applications of the sTR method and for comparison to iMA. The MC algorithm was based on Liebert et al. [18] and is described in detail elsewhere [19]. The following simulations were conducted and are illustrated in Fig. 1:

Fig. 1.

Schemes for the MC simulations to assess the depth sensitivity of sTR: (a) Semi-infinite, multilayered model to generate the sensitivity factors, (b) Semi-infinite, two-layered model used to assess the sensitivity to the bottom layer, and (c) Semi-infinite, three-layered model to assess depth discrimination.

• a)
  Depth sensitivity factors [20] to changes in μ_a located at specific depth were generated for a semi-infinite geometry consisting of a stack of 10 layers, each with a thickness (d) of 0.2 cm (Fig. 1(a)). Initial values of the optical properties for all layers were set to μ_a = 0.1 cm⁻¹, μ_sʹ = 10 cm⁻¹, and a refractive index = 1.4. The sensitivity factors for iMA and sTR for the mean time-of-flight:

  $$MTS{F}_{iMA}=\frac{\Delta <t>}{{\mu }_{a,j}},MTS{F}_{sTR}=\frac{\Delta \left(\partial <t>\right)}{{\mu }_{a,j}}$$ (3)
  and variance:

  $$VS{F}_{iMA}=\frac{\Delta V}{{\mu }_{a,j}},VS{F}_{sTR}=\frac{\Delta \left(\partial V\right)}{{\mu }_{a,j}}$$ (4)

  were calculated [20] by increasing μ_a by 0.01 cm⁻¹ in all consecutive layers j.

• b)The ability of sTR to retrieve the optical properties of the bottom layer of a two-layer medium was assessed (Fig. 1(b)). Simulations were generated with initial values of μ_a1 = 0.1 cm⁻¹, μ_s1ʹ = 10 cm⁻¹ and d₁ = 4.5 cm for the upper layer; and μ_a2 = 0.15 cm⁻¹, μ_s2ʹ = 10 cm⁻¹ and d₂ = 5.5 cm for the lower layer. Successive simulations were carried out while reducing the thickness of the upper layer from 4.5 cm to 0.5 cm.
• c)The final set of simulations was performed to investigate the depth specificity of sTR to changes in μ_a located at specific depth, based on the concept that the sensitivity to a given layer will varying depending on the separation between the detectors (Δr_D). Simulations were conducted using a three-layer model (Fig. 1(c)) with the initial properties: μ_a1 = 0.1 cm⁻¹, μ_s1ʹ = 10 cm⁻¹ and d₁ = 1 cm for the upper layer; μ_a2 = 0.15 cm⁻¹, μ_s2ʹ = 10 cm⁻¹ and d₂ = 0.5 cm for the middle layer; and μ_a3 = 0.1 cm⁻¹, μ_s3ʹ = 10 cm⁻¹ and d₃ = 1 m - (d₁ + d₂) for the lower layer. Simulations were repeated for d₂ = 1 and 1.5 cm.

For each of the scenarios illustrated in Fig. 1, a total of 3∙10⁹ photon packages were simulated. Simulation for a single scenario took approximately an hour on a 12-core 3.4 GHz PC. DTOFs of the diffusely reflected photons were analyzed by calculation of their statistical moments.

2.2 Phantom experiments

To verify the predictions of the MC simulations, experiments were conducted with a liquid phantom with a volume of ~3 dm³ (17.5 x 17.5 x 9 cm). The phantom included two removable membranes made of Mylar film that were used to create two and three-layered models. The phantom layers were filled with solution of water, diffusively scattering component Intralipid-20% (Fresenius Kabi AG, Germany) with a small amount of absorber (Indian Ink) added. The optical properties of the solutions were estimated using procedure proposed and validated in previous studies [21,22].

Data were acquired with a time-resolved system consisting of a picosecond pulsed diode laser (λ = 803 nm, repetition rate = 80 MHz, LDH-P-C series, PicoQuant, Berlin Germany), and two hybrid photomultiplier detectors (PMA Hybrid, PicoQuant, Berlin, Germany) coupled to a multichannel picosecond event timer and a time-correlated single photon counting (TCSPC) module (HydraHarp 400, PicoQuant, Berlin, Germany) [23]. Experiments were carried out with one emission fiber (ϕ = 400 μm, N.A. = 0.22, Fiberoptics Technology, Pomfret, CT, United States) and two custom-made fiber bundles for collection (length = 2 m, N.A. = 0.22, core 200 µm, and 3.6 mm active area; FiberTech Optica, Kitchner, ON, Canada). The optodes were positioned on the surface of the phantom using an in-house 3D printed holder, which provided a range of r_SD values from 1 to 6 cm. The integration time for each measurement was 60 s (i.e., a series of 200 DTOF’s were obtained with an acquisition time = 300 ms).

For the experiments involving the two-layer model the initial optical properties of the phantom were: μ_a1 = μ_a2 = 0.1 cm⁻¹ and μ_s1ʹ = μ_s2ʹ = 10 cm⁻¹, with a 1 cm thick top layer (d₁). Specific amounts of ink were then added to each layer separately to alter their absorption coefficients [22]: first μ_a1 was varied between 0.1 and 0.25 cm⁻¹, then μ_a2 was varied 0.15 to 0.35 cm⁻¹. In a second set of experiments, μ_a1 and μ_s1ʹ were set to 0.1 and 10 cm⁻¹, respectively, and μ_a2 and μ_s2ʹ were 0.15 and 10 cm⁻¹, respectively. Successive measurements were then collected while increasing the thickness of the upper layer from 0.5 cm to 4.5 cm. All experiments were conducted with two source-detector separations r_SD = 3 and 3.5 cm, typical of in vivo studies.

For the three-layered model, the initial optical properties of the Intralipid solutions were μ_a1 = 0.1 cm⁻¹, μ_a2 = 0.15 cm⁻¹, μ_a3 = 0.1 cm⁻¹, and all μ_sʹ values set to 10 cm⁻¹. The initial thicknesses of the top, middle and bottom layers were 0.5, 1 and 7 cm, respectively. DTOFs were acquired from the two detectors at seven r_D2 values (0.5 to 4 cm) with Δr_D = 0.5 cm. The experiment was repeated with the thickness of the top layer increased to 1, 1.5 and 2 cm.

2.3 In vivo study

Data were acquired with the TR-NIRS system described above but modified for activation studies [24]. This consisted of two laser diodes (LDs) operating at λ = 760 nm and 830 nm. Laser pulses from both LDs were coupled into one emission fiber. The system was also equipped with two detection channels, which were built with the same optical and mechanical elements in order to ensure same IRF for the both channels. The detection fiber bundles were placed perpendicular at a distance of 3 and 4 cm with respect to the emission fiber over the left primary motor cortex as based the 10-10 international system for EEG. Three healthy subjects were recruited (male, mean age 31, right handed). The experimental paradigm consisted of five 30-s alternating periods of finger tapping (right hand) and rest to measure the oxygenation change during motor activation. The TR-NIRS data were used to calculated the changes in μ_a as a function of time from the statistical moments of the DTOFs for each detection channel separately (i.e., the iMA method) [25] and by combining the two channels for the sTR method [15]. The μ_a change measured at the two wavelengths were combined to determine the change in ΔHbO2 concentration using published values of the extinction coefficient at 760 and 830 nm. Finally, the contrast-to-noise ratio (CNR) parameter was calculated as the difference between the ΔHbO₂ value during task and rest periods divided by the standard deviation of ΔHbO₂ in the rest periods.

3. Results

3.1 Monte-Carlo simulations

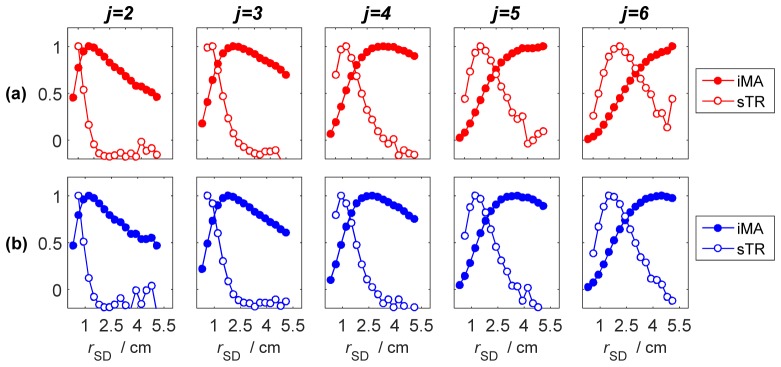
The sensitivity factors derived for sTR are presented in Fig. 2 along with the corresponding sensitivity factors from iMA. Sensitivity factors were generated according to the model shown in Fig. 1(a) by shifting the depth of the perturbation layer (i.e., the 0.2 cm thick layer with the greater μ_a value) from 0.2 cm (j = 2) to 1.2 cm (j = 6). These simulations demonstrate that for a given layer, the sTR method provides greater sensitivity at a shorter source-detector separation compared to that achieved by moment analysis of individual DTOFs. The sensitivity factors for sTR also had a more selective (i.e., narrower) profile compared to iMA. Finally, the separation between the maxima of the sensitivity factors for sTR and iMA increased as the depth of the perturbation layer was increased.

Fig. 2.

Normalized sensitivity factors for (a) mean time-of-flight (MTSF) and (b) variance (VSF). Data are presented for individual layers, denoted by j, of a 10-layer model plotted as a function of source-detector separation. Sensitivity factors were calculated for individual DTOFs (filled circles) and using the moment subtraction approach (open circles, Δr_D = 0.3 cm).

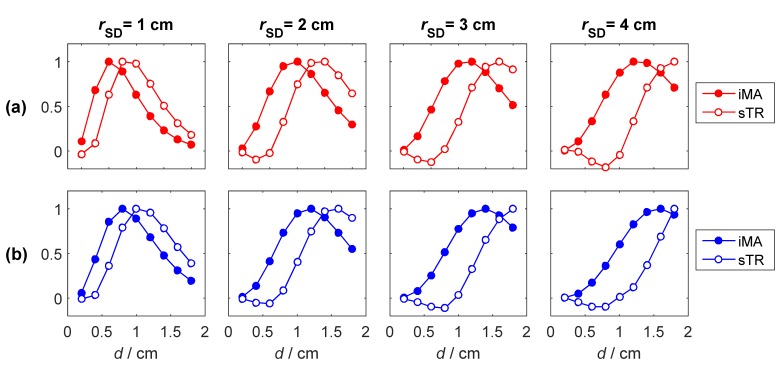
To further illustrate the enhanced depth sensitivity of the sTR method, the normalized sensitivity factors calculated at 4 source-detector separations (r_SD = 1, 2, 3 and 4 cm) are plotted in Fig. 3 as a function of depth of the perturbation layer. It can be observed that for a given r_SD value, the sTR method is more sensitive to deeper layers than iMA. Furthermore, the difference between the two approaches increases as r_SD increases.

Fig. 3.

Sensitivity factors for (a) mean time-of-flight and (b) variance at 4 source-detector separations. The data are presented for the moments of the DTOFs acquired at r_SD (filled circles) and the subtraction of two moments obtained from DTOFS separated by Δr_D = 0.5 cm (open circles). Each curve was normalized to its maximum value.

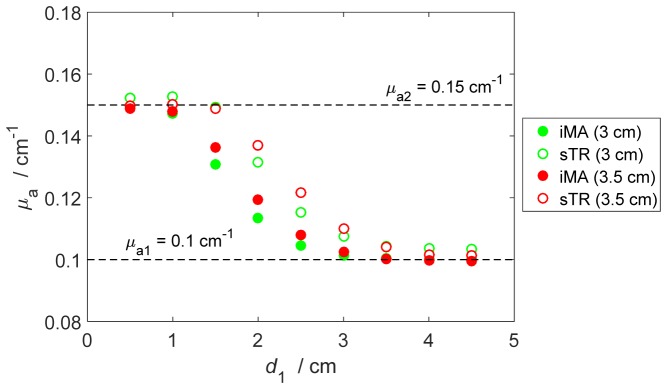
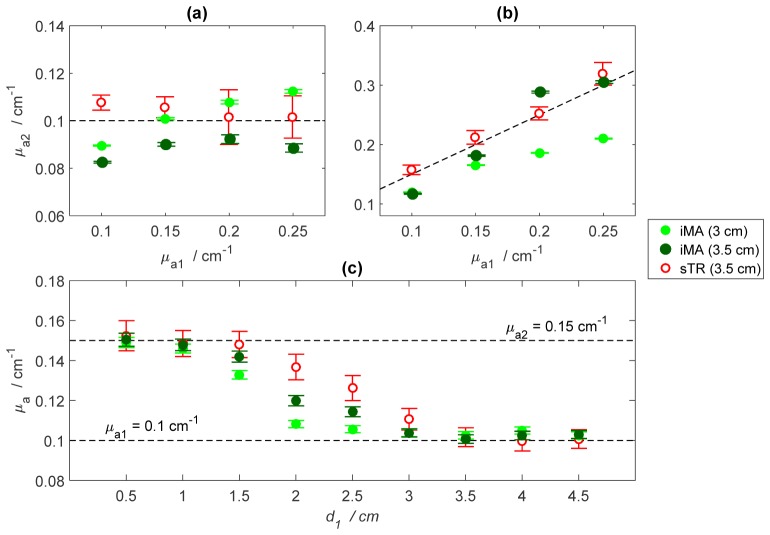
Results of the estimation of μ_a of the bottom layer of a two-layer model obtained from the MC simulations are presented in Fig. 4. In this figure, μ_a values derived from moment analysis are shown as the thickness of the upper layer (d₁) varied from 0.5 to 4.5 cm (shown in Fig. 1(b)). The sTR and iMA methods were applied to DTOFs generated for r_SD values of 3 and 3.5 cm – for the former, Δr_D was 0.5 cm in both cases. Both methods were able to retrieve the μ_a value of the bottom layer when d₁ ≤ 1 cm and, conversely, the estimated μ_a values converged to the upper layer value for d₁ > 3 cm. The greater values of μ_a from sTR compared to those from iMA for d₁ values between 1.5 to 3 cm demonstrate its greater depth sensitivity, which is reflected by the slower convergence to μ_a for the upper layer.

Fig. 4.

Comparison of μ_a values derived from moment analysis of individual DTOFs (filled circles) and the moment subtraction method (open circles). The calculations were carried out for the model presented in Fig. 1(b) for r_SD = 3 cm (green symbols) and r_SD = 3.5 cm (red symbols) with Δr_D = 0.5 cm for the sTR method. The true values of μ_a for the upper (μ_a1) and lower (μ_a2) layers were 0.1 and 0.15 cm⁻¹, respectively.

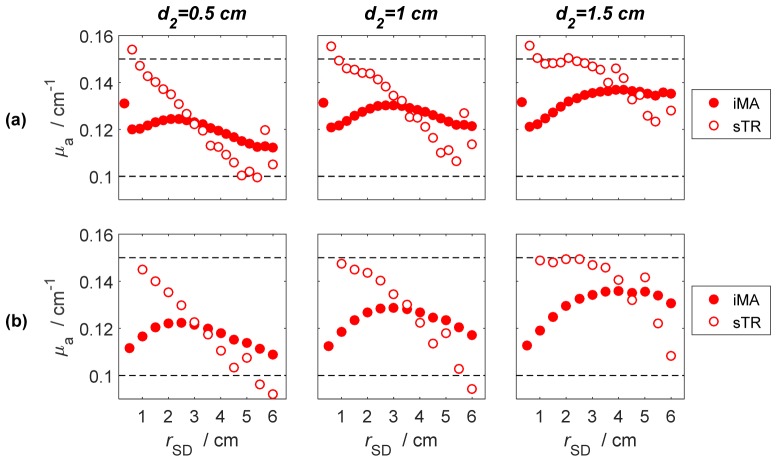
The results of the estimation of μ_a of the middle layer of a three-layer model (shown in Fig. 1(c)) obtained from the MC simulations are presented in Fig. 5. Estimates of μ_a of the middle layer were obtained for three different values of d₂ (0.5, 1.0 and 1.5 cm), which was located at a fixed depth of 1 cm from the top surface, and for the source-detector separations given in Table 1. Photon bundles were collected simultaneously in a set of concentric, consecutive, ring-shaped detectors with fixed width.

Fig. 5.

Comparison of the spatial sensitivity of the moment analysis of individual DTOFs (filed circles) and the moment subtraction method (open circles). The calculations were carried out for (a) Δr_D = 0.3 cm and (b) Δr_D = 0.5 cm. Results are presented for three different thicknesses of the middle layer (d₂ = 0.5-1.5 cm) located at fixed depth 1 cm from the surface of the model and for the source-detector separations given in Table 1. In all simulations μ_a was 0.15 cm⁻¹ for the middle layer and 0.10 cm⁻¹ for the other two layers.

Table 1. Configuration of the source-detector positions used in the three-layer MC simulations.

		iMA			sTR
Detector width		rSD	No. of SD pairs		Detector separation (ΔrD)	rSD	No. of SD pairs
0.3 cm		0.3-6 cm	20		0.3 cm	0.6-6 cm	19
0.5 cm		0.5-6 cm	12		0.5 cm	1-6 cm	11

Because of its greater depth selectivity, the sTR method was able to extract the correct μ_a value of the middle layer at shorter r_SD values (< 2 cm) even when the thickness of the middle layer was only 0.5 cm (Fig. 5(a)). In contrast, μ_a estimates from the iMA method (Fig. 5(b)) were always in between the input values for the middle (0.15 cm⁻¹) and the other two layers (0.10 cm⁻¹), indicating that the method remained sensitive to all layers.

3.2 Phantom experiments

The results of the estimation of μ_a of the bottom layer obtained with the two-layered phantom (Figs. 6 and 7) show similar trends to the MC simulations. For the two-layered structure (shown in Fig. 1(b)), the μ_a estimates derived by applying the sTR method to data acquired at r_SD = 3.5 cm and Δr_D = 0.5 cm were fairly insensitive to μ_a changes in the upper layer (Fig. 6(a)) and were in good agreement with the μ_a values of the bottom layer (Fig. 6(b)). The greater variability observed in the μ_a estimates at μ_a1 > 0.15 cm⁻¹ was due to increased noise in the higher order statistical moments. The results presented in Fig. 4(c) confirm that sTR was able to retrieve μ_a for the bottom layer for d₁ ≤ 1.5 cm while the iMA estimates began to diverge at d₁ = 1 cm. As expected from the MC simulations, estimated μ_a values from both method converged to the upper layer value for d₁ > 3 cm. The difference between the μ_a values estimated from the two source-detector separations observed in Fig. 6(b) can be expalined by the difference in their respective depth sensitivities. For r_SD = 3 cm, the sensitivity to the bottom layer is limited and therefore the measured μ_a value is more heavily weighted to μ_a of the upper layer. The difference between the relative weights for the two source-detector separations becomes more evident as the μ_a value for the bottom layer was increased.

Fig. 6.

Results from the two-layer phantom experiments with absorption changes in (a) the upper layer and (b) the bottom layer. (c) Comparison of μ_a values obtained from the iMA (filled circles) and sTR (open circles) methods. For the sTR method Δr_D = 0.5 cm, and the iMA method was applied to DTOFs acquired at r_SD = 3 cm (green), and r_SD = 3.5 cm (dark green). The error bars represent the standard deviation of μ_a across a series of 200 measured DTOFs.

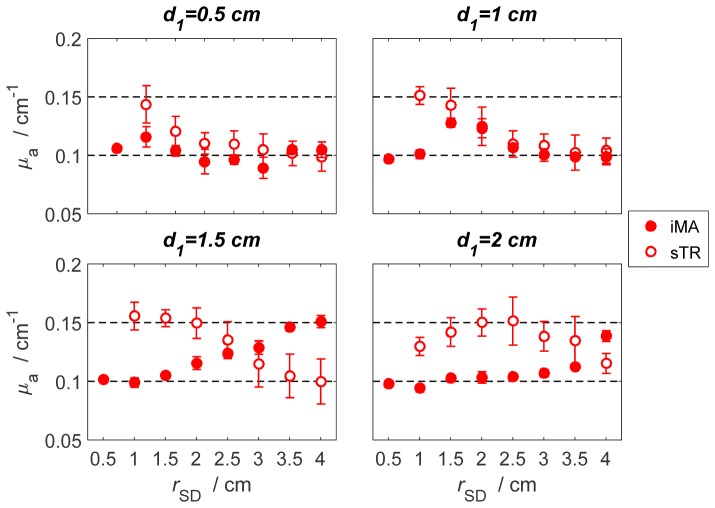
Fig. 7.

Results obtained with the three-layered phantom carried out over a range of thicknesses for the top layer (d₁ = 0.5 - 2 cm). Estimated μ_a values were obtained with the sTR method (open circles) and the iMA method (filled circles). In all cases, μ_a was 0.15 cm⁻¹ for the middle layer and 0.10 cm⁻¹ for the other two layers. The thickness of the middle layer was 1 cm in all cases. The error bars represent standard deviation of μ_a across a series of 200 measured DTOFs.

The estimated μ_a values of the middle layer derived from the sTR and iMA methods applied to data acquired with the three-layered phantom (according to Fig. 1(c)) are presented in Fig. 7. In all cases, which spanned a range of top-layer thicknesses from 0.5 to 2 cm, the sTR method was able to retrieve the μ_a value of the middle layer. The accuracy of sTR depended on both d₁ and r_SD, which demonstrates the depth selectivity of the method. In contrast, the iMA method only converged to the μ_a value of the middle layer in one case (d₁ = 1.5 cm and r_SD ≥ 3.5 cm). In this case, the sTR method converged to the μ_a value of the middle layer at a shorter source-detector separation (r_SD ≤ 2 cm).

3.3 In vivo study

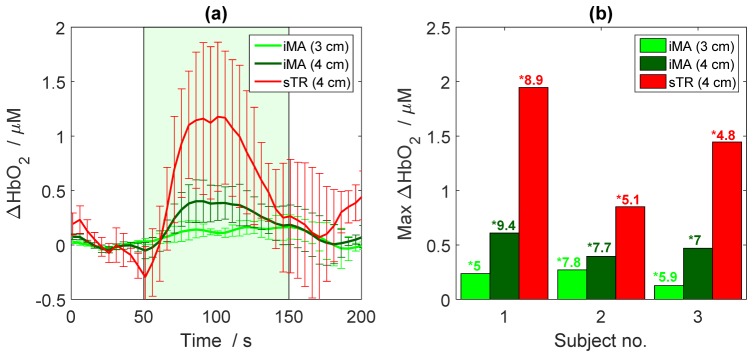
The results of the in vivo studies confirmed the enhanced depth sensitivity of the sTR method predicted by the MC simulations and demonstrated with the tissue-phantom experiments. In all three subjects, the sTR method provided a greater change in oxyhemoglobin concentration (ΔHbO₂) during finger tapping than obtained by analyzing the DTOFs acquired at r_SD of 3 and 4 cm individually by the iMA method (Fig. 8). The maximum ΔHbO₂ was calculated from the mean value between 75 and 125 s relative to the mean baseline value. This signal improvement is similar to that obtained by selecting late time gates [17,26]. It should be noted that the contrast-to-noise ratio (CNR) of the sTR method appeared to be lower than the iMA approach, although this did not reach significance.

Fig. 8.

(a) Increase in oxyhemoglobin concentration (ΔHbO₂) during motor activation determined by iMA applied to each r_SD separately (green lines) and by sTR. Time courses are the average across three subjects. The green box represents the stimulation period. (b) Magnitude of the ΔHbO₂ for each subject calculated by the iMA and sTR techniques. The CNR of each time course is indicated beside an asterisk (*). The error bars represent the standard deviation of ΔHbO₂ across subjects.

4. Discussion

Real-time in vivo assessment of tissue optical properties is one of the crucial advantages of NIRS, particularly for bedside monitoring of brain function. One of the limitations of NIRS for in vivo studies is its limited spatial resolution. This can be overcome using high-density NIRS systems [27,28] based on signals acquired at multiple source-detector distances. However, signals recorded by such systems require rigorous analysis in order to adequately separate scalp and brain signals. To overcome this issue and enhance the sensitivity of NIRS to deeper tissues (i.e., brain), TR methodology has been proposed. It has been previously shown that the sensitivity to deeper tissue can be improved by analyzing the measured DTOFs in terms of higher order statistical moments. The sTR method proposed in an earlier study [15] and applied here is based on maximizing depth sensitivity by combining higher order moment analysis with DTOFs acquired at separate source-detector distances.

The results obtained for the first group of simulations (Figs. 2 and 3) demonstrate that application of the sTR technique increases sensitivity to changes in μ_a located at specific depth at any given source-detector separation. That is, the peak of the sensitivity profile for sTR shifts toward shorter source-detector separations in comparison to the iMA approach. This feature is important because generally greater depth sensitivity is only achieved by increasing the source-detector separation [7], but at the cost of reducing CNR due to lower photon counts. The sTR technique can potentially overcome this limitation since it allows monitoring of deeper tissue compartments with the use of shorter (~2 cm) source-detector separations than iMA approach (~4 cm).

The second set of MC simulations and corresponding phantom experiments (Figs. 4 and 6) focused on evaluating the effectiveness of sTR for detecting absorption changes at greater depths in a turbid medium. The results showed that sTR provide a better response to absorption changes within the medium (for the shorter source-detector separations). Results presented in Fig. 4 shows that sTR is still able to accurately estimate μ_a at a depth of 1.5 cm. In contrast, the iMA applied to DTOFs at a source-detector distance of 3.5 cm underestimates μ_a by 15%. This advantage could be used in future studies as it can potentially prove the usefulness of the sTR technique as a tool for early detection of deeper lesions resulting from stroke or traumatic brain injury. The observed ability of the sTR method for direct measurements of the deeper tissue compartments (e.g., cerebral cortex) can be crucial for CBF monitoring since skull thickness is typically between 1 to 1.5 cm in adults. It should be also pointed out that the results of the MC simulations as well as the phantom experiments prove that the sTR method for r_SD >2 cm is almost insensitive to the superficial layer, which is important in neurophysiological experiments because it provide methodology for elimination of the of systemic contamination [29,30].

The final set of phantom experiments was conducted with different combinations of source-detector distances (r_SD) and detector separations (Δr_D) to assess the depth specificity of sTR; that is, the ability to determine μ_a accurately for a specific optical layer at a given depth and thickness. The enhanced depth specificity provided by sTR is demonstrated by the greater range of μ_a estimates shown in Figs. 5 and 7 as the depth and thickness of the target layer was varied. Figure 7 demonstrates that for a shallow target layer (i.e., d₁ ≤ 1 cm), the sTR converges to the correct μ_a (0.15 cm⁻¹) for short r_SD values only. If this layer is relatively deep (i.e., d₁ = 2 cm), this μ_a value is obtained at r_SD values around 2.5 cm. In contrast, the iMA results did not show the same range of μ_a estimates. Instead, its estimates tended to converge to the μ_a value (0.1 cm⁻¹) of the upper and lower layers (Fig. 7), or to a weighted average of the two μ_a values if the depth of the target layer was constant and its thickness varied (Fig. 5). These results demonstrate that μ_a estimated from higher order moment analysis of a single DTOF is more sensitive to absorption properties over a range of layers compared to the sTR method. Applying the latter method to TR-NIRS data acquired at multiple source-detector distances may provide a means of resolving the different absorption properties of heterogeneous medium – particularly considering the advent of low-cost TR detectors [31].

As an initial in vivo demonstration of the sTR method, a TR-fNIRS experiment was conducted using a simple finger-tapping experiment and acquiring data at source-detector distances of 3 and 4 cm. The results presented in Fig. 8 show that magnitudes of changes in oxyhemoglobin concentration calculated by sTR were considerably higher for all three participants than the corresponding changes determined from the iMA method for each detector separately. Considering that the functional paradigm should elicit minimal hemoglobin changes in scalp, these results show that the sTR method is less sensitive to superficial tissue since the lower ΔHbO₂ obtained by the iMA method is likely due to greater partial-volume errors. This greater depth sensitivity would be advantageous for fNIRS paradigms that produce smaller hemoglobin changes than simple motor tasks [34]. However, the calculated CNR of the sTR method was lower than the analysis of individual DTOFs, which should be considered in future applications.

Funding

This study was supported by the operating grants from the Canadian Institutes of Health Research (CIHR), the Natural Sciences and Engineering Research Council of Canada (NSERC), and the National Institutes of Health (1ROINS082309), as well as a personnel award to K. St. Lawrence from the Heart and Stroke Foundation, Ontario Provincial Office. Involvement of A.L. was supported by the project UMO-2014/15/B/ST7/05276 “Spectral time-resolved measurements for cerebral blood flow assessment” financed by the Polish National Science Center.