Abstract
The purpose of this study was to determine whether the effects of cumulative head impacts during a season of high school football produce changes in diffusional kurtosis imaging (DKI) metrics in the absence of clinically diagnosed concussion. Subjects were recruited from a high school football team and were outfitted with the Head Impact Telemetry System (HITS) during all practices and games. Biomechanical head impact exposure metrics were calculated, including: total impacts, summed acceleration, and Risk Weighted Cumulative Exposure (RWE). Twenty-four players completed pre- and post-season magnetic resonance imaging, including DKI; players who experienced clinical concussion were excluded. Fourteen subjects completed pre- and post-season Immediate Post-Concussion Assessment and Cognitive Testing (ImPACT). DKI-derived metrics included mean kurtosis (MK), axial kurtosis (K axial), and radial kurtosis (K radial), and white matter modeling (WMM) parameters included axonal water fraction, tortuosity of the extra-axonal space, extra-axonal diffusivity (De axial and radial), and intra-axonal diffusivity (Da). These metrics were used to determine the total number of abnormal voxels, defined as 2 standard deviations above or below the group mean. Linear regression analysis revealed a statistically significant relationship between RWE combined probability (RWECP) and MK. Secondary analysis of other DKI-derived and WMM metrics demonstrated statistically significant linear relationships with RWECP after covariate adjustment. These results were compared with the results of DTI-derived metrics from the same imaging sessions in this exact same cohort. Several of the DKI-derived scalars (Da, MK, K axial, and K radial) explained more variance, compared with RWECP, suggesting that DKI may be more sensitive to subconcussive head impacts. No significant relationships between DKI-derived metrics and ImPACT measures were found. It is important to note that the pathological implications of these metrics are not well understood. In summary, we demonstrate a single season of high school football can produce DKI measurable changes in the absence of clinically diagnosed concussion.
Keywords: : concussion, diffusion kurtosis imaging, football, Head Impact Telemetry System, Risk Weighted Cumulative Exposure
Introduction
Football has the highest concussion rate of any competitive contact sport.1 Parents, coaches, and physicians of youth athletes are becoming increasingly concerned about the effects of head impacts. These concerns are reflected in the recent 9.5% decrease in participation in the Pop Warner youth football program.2 While concussion can represent a serious and immediate clinical manifestation of any head impact, the effects of repeated subconcussive impacts on youth and high school populations are largely unknown.
Previous research has focused primarily on collegiate football players.3–7 Recent biomechanical studies of head impacts have shown impact distributions for youth and high school players to be similar to those seen at the collegiate level, with differences primarily in the highest impact magnitudes and total number of impacts.7–9 The effects of these impacts can, in part, be studied through measuring the integrity of white matter, or using diffusion tensor imaging (DTI) derived metrics, which are known to be important in tracking brain development.10 Recently, we demonstrated associations between DTI-derived metric changes and biomechanical head impact metrics over a single season of high school football.11 Bazarian and colleagues found similar changes in DTI-derived metrics that correlated with helmet impact measures over a single season of collegiate football.12
Diffusional kurtosis imaging (DKI) is an extension of DTI that may provide additional information regarding white matter integrity. When diffusion is homogeneous and Gaussian, it can be calculated using the linear estimation methods applied for DTI. However, diffusion in the brain is naturally anisotropic and non-Gaussian due to the effects of the cellular microstructure, particularly myelinated axons. DKI is able to measure the non-Gaussian diffusion by requiring three b values and at least 15 gradient directions. Kurtosis refers, in general, to a dimensionless statistic that quantifies the deviation from a Gaussian, or normal distribution.13 Kurtosis can be used to characterize quantitatively non-Gaussian water diffusion from magnetic resonance imaging (MRI) using a series of equations.14 The diffusional kurtosis pertains specifically to the distribution of molecular displacements associated with a diffusive medium, such as water within brain tissue. A greater degree of structure in the medium tends to cause more deviations from Gaussian movement and typically increases the diffusional kurtosis.15 Because water diffusion in the brain is anisotropic, particularly in white matter, the diffusional kurtosis depends on the direction in which the diffusion is measured.
DKI-derived metrics include mean kurtosis (MK), axial kurtosis (K axial), and radial kurtosis (K radial).16 MK is the mean, over all diffusion directions, of the measured diffusional kurtosis. K axial is measured along the principal diffusion tensor eigenvector, while K radial is the average measured kurtosis over all directions perpendicular to the principal eigenvector. The principal diffusion tensor eigenvector is the direction that maximizes the diffusivity; in white matter regions with unidirectional axons, it generally will be oriented parallel to the axons, which is the basis of white matter fiber tractography.17
These kurtosis parameters apply to any diffusive medium and reflect the physics of the diffusion dynamics. By augmenting these with tissue modeling assumptions for brain microstructure, additional metrics can be calculated that have more specific biological interpretations.18 One simple example, which we call the white matter modeling (WMM) method, assumes that the axons are unidirectional and that brain tissue water can effectively be divided into two non-exchanging pools corresponding to the intra-axonal space and extra-axonal space (EAS).31 The combination of DKI and WMM allows for the calculation of several model parameters, including the axonal water fraction (AWF), the tortuosity of the EAS, the extra-axonal diffusivities (De axial and radial), and the intra-axonal diffusivity. AWF represents the fraction of the water signal in the axons relative to the total water signal. Tortuosity measures the ratio of diffusion along the direction of the fibers and the diffusion perpendicular to the fibers in the EAS; it is expected to be sensitive to the myelinated axonal fraction, which increases with increasing myelin and axonal density.
DKI-derived metrics have been used to study early development, autism spectrum disorders, attention-deficit/hyperactivity disorder, Alzheimer's disease, and traumatic brain injury (TBI).19–23 These studies suggest that DKI-derived metrics can provide a more sensitive imaging biomarker to assess the changes in microstructure in the brain. MK increases with age, as expected for brain development; however, other metrics are not well studied in the adolescent age group.19,22 Stokum and colleagues showed decreases in MK and K radial, from 10 days post-injury to 6 months post-injury, in subjects with TBI, compared with controls.21 Grossman and colleagues also showed decreases in MK in subjects scanned within 1 year post-injury, compared with controls.24 In contrast, Zhuo and colleagues showed increases in MK from baseline in rats scanned 7 days post-injury, which coincided with increases in K axial and decreases in K radial.25
Concussion, or mild traumatic brain injury (mTBI), is typically a clinical diagnosis. However, in order to study the more subtle effects of subconcussive head impacts, an effective method of measuring the biomechanical forces associated with each head impact is required. To acquire this information, many investigators have used the Head Impact Telemetry System (HITS). The HITS collects real-time data during on-field play, and has been implemented at the youth, high school, and collegiate levels.3–6,8,26,27 It consists of a base unit, placed beside the field, and helmet-embedded encoders that are designed such that the sensors remain in contact with the head to ensure measurement of head acceleration rather than helmet acceleration. These helmet-embedded sensor systems collect data on number of impacts, time between impacts, as well as peak resultant linear acceleration and estimated peak resultant rotational acceleration, which is sent to the base unit in real-time. This data is then analyzed in terms of the peak acceleration, impact location, and other biomechanical indicators.
The primary aim of this study was to determine if the cumulative effects of head impacts from a season of high school varsity football can produce DKI detectable changes in the brain in the absence of clinically diagnosed concussion. The primary hypothesis was that there would be a significant association between the cumulative head impact exposure of an athlete and DKI-derived metrics, due to an alteration in microstructural complexity related to axonal injury.25 Additionally, we compared the DKI metrics to DTI metrics from a previous study computed in the same cohort.
Methods
Protocol summary
The HITS data collection, imaging acquisition, cognitive testing, and subjects for this paper are identical to that of Davenport and colleagues11 and are abbreviated here.7 The calculation of DKI scalar metrics differs and is explained in more detail.
All subjects (n = 24, male; mean age = 16.9) were fitted with the HITS for acquisition of biomechanical exposure data during all practices and games. From this data, Risk Weighted Cumulative Exposure (RWE) was calculated.7 This metric represents the cumulative concussion risk for each impact for each player over the course of the season. The RWE can be calculated separately from the linear, rotational, and combined probability risk functions and is referred to as RWELinear, RWERotational, and RWECP respectively.28,29 Our primary hypothesis relates to changes in the brain associated with RWECP. RWECP is based on the combined probability associated with the peak resultant linear and rotational acceleration components of each head impact. In addition, all participants received baseline, pre-season, and post-season MRI and ImPACT neuropsychologic testing.
ImPACT cognitive testing protocol
Neuropsychological testing was administered pre- and post-season using version 2.1 of the ImPACT computer test battery at the high school computer laboratory under the supervision of the team's athletic trainer.30,31 Ten of the 24 subjects did not return for post-season ImPACT testing, leaving 14 subjects (mean age, 17.03) with complete pre- and post-season testing. The outcome measures include Verbal Memory, Visual Memory, Visual Motor (Processing Speed), and Reaction Time.
MRI acquisition and processing
MRI data was acquired on a 3 Tesla Siemens Skyra MRI scanner using a 32-channel human head/neck coil (Siemens Medical, Erlangen, Germany) in accordance with the National Institute of Neurological Disorders and Stroke Common Data Elements specification. T1-weighted images were obtained for anatomic correlation using a 3D volumetric Magnetization Prepared Rapid Acquisition Gradient Echo sequence with isotropic resolution of 0.9 mm3: repetition time (TR) = 1900 msec; echo time (TE) = 2.93 msec; inversion time (TI) = 900 msec; flip angle = 9 degrees; slices = 176. Diffusion-weighted data were acquired using a two-dimensional single-shot EPI sequence (TR = 10,500 msec; TE = 99 msec; flip angle = 90 degrees; spatial resolution = 2.2 × 2.2 mm2; slice thickness = 3 mm; slices = 54; 10 b = 0 volumes; 15 diffusion directions with b = 1000/2000 sec/mm2 each). The additional b value of 2000 provided for computation of DKI metrics.
Pre-processing of diffusion tensor images was performed using FMRIB Software Library.32 All DKI-derived and WMM metrics were calculated using the Diffusion Kurtosis Estimator (DKE).33 Images were corrected for distortion by normalizing the B0 image to the T1 image and subsequently applying the transform to the DKE output images. These scalar maps were then normalized to MNI space based on parameters from an SPM8 normalization of the corresponding T1-weighted structural images. WMM metrics were masked to only allow white matter voxels with fractional anisotropy (FA) above 0.4, in accordance with the model assumptions.34 DKI-derived metrics were masked for whole–brain, white matter, and gray matter for separate analysis. All images were visually inspected to ensure quality of processing procedures. Delta maps (post-season minus pre-season), were computed for each DKI and WMM metric. The group mean and standard deviation of the delta maps were used to calculate voxel-wise Z-scores thresholded at ±2 SD.11 This provides a single number representing the total number of abnormal voxels for each subject and each scalar metric to be used in the regression analysis.
Comparison of biomechanics and imaging data
Linear regression analyses were performed to study the relationship between cumulative exposure metrics and DKI-derived and WMM metrics using JMP (SAS Institute Inc., Cary, NC). Secondary analyses with RWELinear and RWERotational, and DKI-derived and WMM measures also were performed to better characterize any associations. In the primary analysis, the number of abnormal MK voxels was used as a dependent variable. A log transformation was applied in order to satisfy assumptions of normality. Age at pre-season, body mass index (BMI), and time between scans were used as covariates. No outliers were identified in any linear regression performed based on the Cook's distance of each point.
No corrections were made for multiple comparisons, as our primary hypothesis centered on the relationship between RWE and MK.
Comparison of cognitive testing and imaging data
The delta (post- season minus pre-season) of each ImPACT outcome measure also was computed (Verbal Memory, Visual Memory, Visual Motor [Processing Speed], and Reaction Time). The delta scores were then individually, compared with the number of abnormal DKI voxels using the Spearman's rank correlation coefficient.
Results
Our primary hypothesis focused on changes in MK associated with RWECP. This association explained 4% of the total variance in the whole–brain (Table 1B; p = 0.3507). Covariate adjustment for age, BMI, and time between scans increased the strength of this relationship to explain 66% of variance (p < 0.0001). RWECP also demonstrated a significant relationship with AWF (R2 = 0.20; p = 0.0268). The strength of this relationship increased after covariate adjustment for time between scans, age, and BMI (R2 = 0.51; p = 0.0013). Other DKI-derived and WMM metrics (MK, K axial, K radial, and De axial, De radial, Da) also achieved significance after covariate adjustment. The relationship between RWECP and its subcomponents with respect to tortuosity did not achieve significance. The linear component of RWE similarly achieved significance for many of these metrics, except for De axial (Table 1A; p = 0.0675). Relationships between RWELinear and whole–brain DKI-derived metrics (MK, K axial, and K radial) were all significant (Table 1B). For the rotational component of RWE, only whole–brain and gray matter DKI-derived metrics achieved significance (Tables 1B, 1D).
Table 1B.
Associations Between HITS Metrics and Changes in DKI-Derived Metrics in WHOLE BRAIN (± SD 2.0)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| MK vs. RWECP | 0.0397 | 0.3507 | 0.6598 | 0.4572 | < 0.0001* |
| K axial vs. RWECP | 0.0578 | 0.2577 | 0.6284 | 0.4712 | 0.0001* |
| K radial vs. RWECP | 0.0302 | 0.4169 | 0.5933 | 0.3760 | 0.0002* |
| MK vs. RWELinear | 0.0038 | 0.7738 | 0.6079 | 0.3745 | 0.0002* |
| K axial vs. RWELinear | 0.0109 | 0.6267 | 0.5732 | 0.3926 | 0.0004* |
| K radial vs. RWELinear | 0.0015 | 0.8580 | 0.5508 | 0.3108 | 0.0006* |
| MK vs. RWERotational | 0.0591 | 0.2523 | 0.5014 | 0.2045 | 0.0014* |
| K axial vs. RWERotational | 0.0397 | 0.3503 | 0.4019 | 0.1487 | 0.0072* |
| K radial vs. RWERotational | 0.0552 | 0.2691 | 0.4811 | 0.2039 | 0.0021* |
| MK vs. total impacts | 0.0066 | 0.7055 | 0.5297 | 0.2497 | 0.0009* |
| K axial vs. total impacts | 0.0116 | 0.6166 | 0.4770 | 0.2557 | 0.0022* |
| K radial vs. total impacts | 0.0051 | 0.7402 | 0.5023 | 0.2364 | 0.0014* |
| MK vs. summed linear acceleration | 0.0051 | 0.7405 | 0.5466 | 0.4444 | 0.0006* |
| K axial vs. summed linear acceleration | 0.0099 | 0.6430 | 0.4977 | 0.4482 | 0.0015* |
| K radial vs. summed linear acceleration | 0.0031 | 0.7949 | 0.5112 | 0.413935 | 0.0012* |
| MK vs. summed rotational acceleration | 0.0103 | 0.6373 | 0.5548 | 0.4456 | 0.0005* |
| K axial vs. summed rotational acceleration | 0.0165 | 0.5502 | 0.5063 | 0.4517 | 0.0013* |
| K radial vs. summed rotational acceleration | 0.0071 | 0.6961 | 0.5169 | 0.4141 | 0.0011* |
p < 0.05. Bold p values.
HITS, Head Impact Telemetry System; DKI, diffusional kurtosis imaging; SD, standard deviation; BMI, body mass index; MK, mean kurtosis; RWEcp, Risk Weighted Cumulative Exposure combined probability; K axial, axial kurtosis; K radial, radial kurtosis.
Table 1A.
Associations Between HITS Metrics and Changes in WMM Metrics in White Matter Areas with FA >0.4 (± SD 2.0)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| AWF vs. RWECP | 0.2039 | 0.0268* | 0.5069 | 0.5237 | 0.0013* |
| Tortuosity vs. RWECP | 0.1895 | 0.0335* | 0.3401 | 0.4050 | 0.0167* |
| De axial vs. RWECP | 0.1799 | 0.0389* | 0.4212 | 0.4513 | 0.0054* |
| De radial vs. RWECP | 0.1410 | 0.0706 | 0.4209 | 0.4193 | 0.0054* |
| Da vs. RWECP | 0.2391 | 0.0153* | 0.6412 | 0.6415 | < 0.0001* |
| AWF vs. RWELinear | 0.0839 | 0.1697 | 0.2861 | 0.3105 | 0.0324* |
| Tort vs. RWELinear | 0.0666 | 0.2233 | 0.1354 | 0.2204 | 0.1518 |
| De axial vs. RWELinear | 0.0614 | 0.2432 | 0.2198 | 0.2603 | 0.0675 |
| De radial vs. RWELinear | 0.0491 | 0.2979 | 0.3085 | 0.3066 | 0.0248* |
| Da vs. RWELinear | 0.0830 | 0.1721 | 0.3944 | 0.3949 | 0.0080* |
| AWF vs. RWERotational | 0.0840 | 0.1696 | 0.0946 | 0.1255 | 0.2151 |
| Tortuosity vs. RWERotational | 0.0683 | 0.2173 | 0.0101 | 0.1074 | 0.4039 |
| De axial vs. RWERotational | 0.0880 | 0.1593 | 0.1038 | 0.1504 | 0.1993 |
| De radial vs. RWERotational | 0.0871 | 0.1615 | 0.2358 | 0.2336 | 0.0570 |
| Da vs. RWERotational | 0.0064 | 0.7096 | 0.0295 | 0.0304 | 0.3532 |
| AWF vs. total impacts | 0.0127 | 0.5997 | 0.0034 | 0.0374 | 0.4225 |
| Tortuosity vs. total impacts | 0.0110 | 0.6264 | −0.0654 | 0.0393 | 0.6358 |
| De axial vs. total impacts | 0.0041 | 0.7664 | −0.0222 | 0.0310 | 0.4970 |
| De radial vs. total impacts | 0.0018 | 0.8448 | 0.0701 | 0.0675 | 0.2614 |
| Da vs. total impacts | 0.0067 | 0.7033 | 0.0672 | 0.0680 | 0.2674 |
| AWF vs. summed linear acceleration | 0.0244 | 0.4664 | 0.0504 | 0.1181 | 0.3037 |
| Tortuosity vs. summed linear acceleration | 0.0182 | 0.5296 | −0.0340 | 0.1054 | 0.5335 |
| De axial vs. summed linear acceleration | 0.0116 | 0.6171 | 0.0175 | 0.1138 | 0.3841 |
| De radial vs. summed linear acceleration | 0.0078 | 0.6812 | 0.1224 | 0.2173 | 0.1701 |
| Da vs. summed linear acceleration | 0.0167 | 0.5476 | 0.1281 | 0.2151 | 0.1619 |
| AWF vs. summed rotational acceleration | 0.0232 | 0.4774 | 0.0434 | 0.1072 | 0.3196 |
| Tortuosity vs. summed rotational acceleration | 0.0203 | 0.5067 | −0.0337 | 0.1029 | 0.5327 |
| De axial vs. summed rotational acceleration | 0.0104 | 0.6349 | 0.0081 | 0.0982 | 0.4092 |
| De radial vs. summed rotational acceleration | 0.0072 | 0.6929 | 0.1072 | 0.1902 | 0.1936 |
| Da vs. summed rotational acceleration | 0.0203 | 0.5062 | 0.1318 | 0.2152 | 0.1567 |
p < 0.05. Bold p values.
HITS, Head Impact Telemetry System; WMM, white matter modeling; FA, fractional anisotropy; SD, standard deviation; BMI, body mass index; AWF, axonal water fraction; RWEcp, Risk Weighted Cumulative Exposure combined probability; De axial and radial, extra-axonal diffusivity; Da, intra-axonal diffusivity.
Table 1D.
Associations Between HITS Metrics and Changes in DKI-Derived Metrics in Gray Matter (± SD 2.0)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-Adjusted R2 | p value | |
| MK vs. RWECP | 0.0271 | 0.4419 | 0.6575 | 0.4182 | < 0.0001* |
| K axial vs. RWECP | 0.0455 | 0.3171 | 0.6125 | 0.4339 | 0.0001* |
| K radial vs. RWECP | 0.0199 | 0.5112 | 0.5975 | 0.3443 | 0.0002* |
| MK vs. RWELinear | 0.0018 | 0.8449 | 0.6328 | 0.3762 | < 0.0001* |
| K axial vs. RWELinear | 0.0081 | 0.6767 | 0.5747 | 0.3786 | 0.0003* |
| K radial vs. RWELinear | 0.0003 | 0.9360 | 0.5756 | 0.3086 | 0.0003* |
| MK vs. RWERotational | 0.0539 | 0.2751 | 0.5336 | 0.2077 | 0.0008* |
| K axial vs. RWERotational | 0.0431 | 0.3306 | 0.4218 | 0.1552 | 0.0053* |
| K radial vs. RWERotational | 0.0517 | 0.2853 | 0.5168 | 0.2127 | 0.0011* |
| MK vs. total impacts | 0.0067 | 0.7033 | 0.5841 | 0.2934 | 0.0003* |
| K axial vs. total impacts | 0.0135 | 0.5890 | 0.5052 | 0.2771 | 0.0013* |
| K radial vs. total impacts | 0.0047 | 0.7508 | 0.5515 | 0.2693 | 0.0006* |
| MK vs. summed linear acceleration | 0.0047 | 0.7505 | 0.5964 | 0.4562 | 0.0002* |
| K axial vs. summed linear acceleration | 0.0108 | 0.6293 | 0.5210 | 0.4645 | 0.0010* |
| K radial vs. summed linear acceleration | 0.0024 | 0.8186 | 0.5558 | 0.4500 | 0.0005* |
| MK vs. summed rotational acceleration | 0.0100 | 0.6437 | 0.6042 | 0.4918 | 0.0002* |
| K axial vs. summed rotational acceleration | 0.0178 | 0.5338 | 0.5305 | 0.4692 | 0.0008* |
| K radial vs. summed rotational acceleration | 0.0062 | 0.7157 | 0.5614 | 0.4499 | 0.0005* |
p < 0.05. Bold p values.
HITS, Head Impact Telemetry System; DKI, diffusional kurtosis imaging; SD, standard deviation; BMI, body mass index; MK, mean kurtosis; RWEcp, Risk Weighted Cumulative Exposure combined probability; K axial, axial kurtosis; K radial, radial kurtosis.
Tables 1A-D were computed based on two tails of the distribution, examining both increases and decreases (± 2 SD) in DKI-derived and WMM metrics. The metrics in Table 1A were calculated for areas where FA >0.4, whereas Table 1B includes all voxels within the brain. Table 1C is for WM voxels only and Table 1D is for gray matter voxels only. We performed additional analyses of the DKI-derived and WMM metrics examining only increases (+ 2 SD) shown in Tables 2A-D, and only decreases (- 2SD) shown in Tables 3A-D.
Table 1C.
Associations Between HITS Metrics and Changes in DKI-Derived Metrics in White Matter (± SD 2.0)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| MK vs. RWECP | 0.1411 | 0.0705 | 0.4993 | 0.4807 | 0.0015* |
| K axial vs. RWECP | 0.1891 | 0.0337* | 0.5735 | 0.5597 | 0.0004* |
| K radial vs. RWECP | 0.1474 | 0.0640 | 0.4024 | 0.4194 | 0.0071* |
| MK vs. RWELinear | 0.0347 | 0.3837 | 0.2699 | 0.2427 | 0.0391* |
| K axial vs. RWELinear | 0.0398 | 0.3497 | 0.3342 | 0.3126 | 0.0180* |
| K radial vs. RWELinear | 0.0443 | 0.3233 | 0.3438 | 0.2283 | 0.0779 |
| MK vs. RWERotational | 0.0769 | 0.1894 | 0.1604 | 0.1291 | 0.1210 |
| K axial vs. RWERotational | 0.0004 | 0.9252 | 0.0642 | 0.0339 | 0.2736 |
| K radial vs. RWERotational | 0.0612 | 0.2438 | 0.0713 | 0.0977 | 0.2590 |
| MK vs. total impacts | 0.0073 | 0.6923 | 0.0739 | 0.0394 | 0.2539 |
| K axial vs. total impacts | 0.0006 | 0.9134 | 0.0714 | 0.0413 | 0.2588 |
| K radial vs. total impacts | 0.0128 | 0.5984 | 0.0253 | 0.0530 | 0.3640 |
| MK vs. summed linear acceleration | 0.0104 | 0.6360 | 0.1036 | 0.1116 | 0.1996 |
| K axial vs. summed linear acceleration | 0.0001 | 0.0029 | 0.1084 | 0.1670 | 0.1917 |
| K radial vs. summed linear acceleration | 0.0170 | 0.3798 | 0.0554 | 0.1288 | 0.2926 |
| MK vs. summed rotational acceleration | 0.0129 | 0.5972 | 0.1072 | 0.1143 | 0.1937 |
| K axial vs. summed rotational acceleration | 0.0005 | 0.9178 | 0.1085 | 0.1630 | 0.1916 |
| K radial vs. summed rotational acceleration | 0.0197 | 0.5129 | 0.0572 | 0.1279 | 0.2886 |
p < 0.05. Bold p values.
HITS, Head Impact Telemetry System; DKI, diffusional kurtosis imaging; SD, standard deviation; BMI, body mass index; MK, mean kurtosis; RWEcp, Risk Weighted Cumulative Exposure combined probability; K axial, axial kurtosis; K radial, radial kurtosis.
Table 2A.
Associations Between HITS Metrics and Changes in WMM Metrics in White Matter Areas With FA >0.4 (> 2 SD)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| AWF vs. RWECP | 0.2129 | 0.0232* | 0.3937 | 0.4438 | 0.0081* |
| Tortuosity vs. RWECP | 0.1107 | 0.1122 | 0.1578 | 0.2528 | 0.1239 |
| De axial vs. RWECP | 0.1549 | 0.0571 | 0.3412 | 0.3494 | 0.0165* |
| De radial vs. RWECP | 0.1285 | 0.0854 | 0.4076 | 0.3927 | 0.0066* |
| Da vs. RWECP | 0.2485 | 0.0132* | 0.5408 | 0.5609 | 0.0007* |
| AWF vs. RWELinear | 0.0459 | 0.3146 | 0.1443 | 0.2150 | 0.1402 |
| Tort vs. RWELinear | 0.0337 | 0.3902 | 0.0321 | 0.1412 | 0.3469 |
| De axial vs. RWELinear | 0.0703 | 0.2106 | 0.2102 | 0.2200 | 0.0744 |
| De radial vs. RWELinear | 0.0554 | 0.2683 | 0.2858 | 0.2679 | 0.0326* |
| Da vs. RWELinear | 0.0795 | 0.1819 | 0.3142 | 0.3442 | 0.0232* |
| AWF vs. RWERotational | 0.0145 | 0.5756 | 0.1013 | 0.0019 | 0.7116 |
| Tortuosity vs. RWERotational | 0.0255 | 0.4560 | −0.0637 | 0.0562 | 0.6303 |
| De axial vs. RWERotational | 0.0922 | 0.1492 | 0.0565 | 0.0682 | 0.2900 |
| De radial vs. RWERotational | 0.1113 | 0.1112 | 0.1525 | 0.1312 | 0.1302 |
| Da vs. RWERotational | 0.0001 | 0.9635 | 0.1406 | 0.0052 | 0.5537 |
| AWF vs. total impacts | 0.0004 | 0.9298 | −0.0635 | 0.0243 | 0.6295 |
| Tortuosity vs. total impacts | 0.0038 | 0.7749 | −0.0951 | 0.0283 | 0.7357 |
| De axial vs. total impacts | 0.0159 | 0.5575 | 0.0282 | 0.0402 | 0.3566 |
| De radial vs. total impacts | 0.0071 | 0.6964 | 0.0594 | 0.0358 | 0.2838 |
| Da vs. total impacts | 0.0027 | 0.8086 | 0.0256 | 0.0683 | 0.3632 |
| AWF vs. summed linear acceleration | 0.0003 | 0.9395 | −0.0389 | 0.1024 | 0.5491 |
| Tortuosity vs. summed linear acceleration | 0.0067 | 0.7039 | −0.0756 | 0.0815 | 0.6699 |
| De axial vs. summed linear acceleration | 0.0315 | 0.4069 | 0.0682 | 0.0928 | 0.2653 |
| De radial vs. summed linear acceleration | 0.0175 | 0.5381 | 0.1029 | 0.1166 | 0.2008 |
| Da vs. summed linear acceleration | 0.0109 | 0.6278 | 0.0804 | 0.2155 | 0.2411 |
| AWF vs. summed rotational acceleration | 0.0017 | 0.8463 | −0.0292 | 0.1137 | 0.5187 |
| Tortuosity vs. summed rotational acceleration | 0.0097 | 0.6463 | −0.0693 | 0.0873 | 0.6488 |
| De axial vs. summed rotational acceleration | 0.0339 | 0.3891 | 0.0637 | 0.0823 | 0.2746 |
| De radial vs. summed rotational acceleration | 0.0152 | 0.5666 | 0.0884 | 0.0921 | 0.2261 |
| Da vs. summed rotational acceleration | 0.0173 | 0.5397 | 0.0935 | 0.2263 | 0.2169 |
p < 0.05 Bold p values.
HITS, Head Impact Telemetry System; WMM, white matter modeling; FA, fractional anisotropy; SD, standard deviation; BMI, body mass index; AWF, axonal water fraction; RWEcp, Risk Weighted Cumulative Exposure combined probability; De axial and radial, extra-axonal diffusivity; Da, intra-axonal diffusivity.
Table 2B.
Associations Between HITS Metrics and Changes in DKI-Derived Metrics in Whole–Brain (> 2 SD)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| MK vs. RWECP | 0.0942 | 0.1446 | 0.4630 | 0.3523 | 0.0028* |
| K axial vs. RWECP | 0.1163 | 0.1030 | 0.4830 | 0.4052 | 0.0020* |
| K radial vs. RWECP | 0.0738 | 0.1992 | 0.4675 | 0.3208 | 0.0026* |
| MK vs. RWELinear | 0.0285 | 0.4304 | 0.3073 | 0.1645 | 0.0252* |
| K axial vs. RWELinear | 0.0469 | 0.3092 | 0.3165 | 0.2136 | 0.0225* |
| K radial vs. RWELinear | 0.0216 | 0.4934 | 0.3391 | 0.1570 | 0.0169* |
| MK vs. RWERotational | 0.0772 | 0.1888 | 0.1828 | 0.0143 | 0.0978 |
| K axial vs. RWERotational | 0.1044 | 0.1236 | 0.1649 | 0.0391 | 0.1160 |
| K radial vs. RWERotational | 0.0655 | 0.2273 | 0.2210 | 0.0063 | 0.0666 |
| MK vs. total impacts | 0.0265 | 0.4473 | 0.2058 | 0.0421 | 0.0778 |
| K axial vs. total impacts | 0.0463 | 0.3125 | 0.1876 | 0.0653 | 0.0933 |
| K radial vs. total impacts | 0.0253 | 0.4578 | 0.2534 | 0.0476 | 0.0471* |
| MK vs. summed linear acceleration | 0.0313 | 0.4084 | 0.2251 | 0.0294 | 0.0638 |
| K axial vs. summed linear acceleration | 0.0495 | 0.2963 | 0.2099 | 0.0652 | 0.0747 |
| K radial vs. summed linear acceleration | 0.0291 | 0.4254 | 0.2711 | 0.0295 | 0.0386* |
| MK vs. summed rotational acceleration | 0.0379 | 0.3623 | 0.2289 | 0.0304 | 0.0613 |
| K axial vs. summed rotational acceleration | 0.0572 | 0.2603 | 0.2154 | 0.0681 | 0.0706 |
| K radial vs. summed rotational acceleration | 0.0351 | 0.3804 | 0.2735 | 0.0281 | 0.0376* |
p < 0.05. Bold p values.
HITS, Head Impact Telemetry System; DKI, diffusional kurtosis imaging; SD, standard deviation; BMI, body mass index; MK, mean kurtosis; RWEcp, Risk Weighted Cumulative Exposure combined probability; K axial, axial kurtosis; K radial, radial kurtosis.
Table 2C.
Associations Between HITS Metrics and Changes in DKI-Derived Metrics in White Matter (> 2 SD)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| MK vs. RWECP | 0.1010 | 0.1302 | 0.3240 | 0.3166 | 0.0205* |
| K axial vs. RWECP | 0.1818 | 0.0378* | 0.4917 | 0.4924 | 0.0017* |
| K radial vs. RWECP | 0.1119 | 0.1102 | 0.3032 | 0.3200 | 0.0265* |
| MK vs. RWELinear | 0.0001 | 0.9803 | 0.0793 | 0.0692 | 0.2433 |
| K axial vs. RWELinear | 0.0152 | 0.5660 | 0.1836 | 0.1847 | 0.0970 |
| K radial vs. RWELinear | 0.0032 | 0.7937 | 0.0777 | 0.1000 | 0.2463 |
| MK vs. RWERotational | 0.0628 | 0.2376 | 0.0723 | 0.0622 | 0.2570 |
| K axial vs. RWERotational | 0.0082 | 0.6742 | −0.0012 | 0.0001 | 0.4354 |
| K radial vs. RWERotational | 0.0558 | 0.2664 | 0.0351 | 0.0584 | 0.3395 |
| MK vs. total impacts | 0.0370 | 0.03679 | 0.0113 | 0.0005 | 0.4006 |
| K axial vs. total impacts | 0.0155 | 0.5621 | 0.0019 | 0.0032 | 0.4265 |
| K radial vs. total impacts | 0.0169 | 0.5450 | −0.0239 | 0.0009 | 0.5022 |
| MK vs. summed linear acceleration | 0.0273 | 0.4407 | 0.0118 | 0.0004 | 0.3993 |
| K axial vs. summed linear acceleration | 0.0078 | 0.6812 | 0.1866 | 0.0588 | 0.3898 |
| K radial vs. summed linear acceleration | 0.0111 | 0.6227 | 0.1590 | 0.0223 | 0.4845 |
| MK vs. summed rotational acceleration | 0.0163 | 0.5527 | 0.0152 | 0.0157 | 0.3903 |
| K axial vs. summed rotational acceleration | 0.0039 | 0.7710 | 0.0208 | 0.0605 | 0.3754 |
| K radial vs. summed rotational acceleration | 0.0059 | 0.7204 | −0.0136 | 0.0329 | 0.4712 |
p < .05. Bold p values.
HITS, Head Impact Telemetry System; DKI, diffusional kurtosis imaging; SD, standard deviation; BMI, body mass index; MK, mean kurtosis; RWEcp, Risk Weighted Cumulative Exposure combined probability; K axial, axial kurtosis; K radial, radial kurtosis.
Table 2D.
Associations Between HITS Metrics and Changes in DKI-Derived Metrics in Gray Matter (> 2 SD)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| MK vs. RWECP | 0.0849 | 0.1671 | 0.4412 | 0.3193 | 0.0040* |
| K axial vs. RWECP | 0.1077 | 0.1174 | 0.4590 | 0.3729 | 0.0030* |
| K radial vs. RWECP | 0.0608 | 0.2454 | 0.4372 | 0.2769 | 0.0042* |
| MK vs. RWELinear | 0.0333 | 0.3937 | 0.3106 | 0.1602 | 0.0242* |
| K axial vs. RWELinear | 0.0508 | 0.2898 | 0.3095 | 0.1996 | 0.0245* |
| K radial vs. RWELinear | 0.0216 | 0.4927 | 0.3324 | 0.1424 | 0.0184* |
| MK vs. RWERotational | 0.0985 | 0.1352 | 0.1952 | 0.0196 | 0.0866 |
| K axial vs. RWERotational | 0.1204 | 0.0966 | 0.1712 | 0.0393 | 0.1093 |
| K radial vs. RWERotational | 0.0826 | 0.1734 | 0.2294 | 0.0101 | 0.0610 |
| MK vs. total impacts | 0.0397 | 0.3507 | 0.2195 | 0.0492 | 0.0676 |
| K axial vs. total impacts | 0.0594 | 0.2512 | 0.1938 | 0.0655 | 0.0878 |
| K radial vs. total impacts | 0.0332 | 0.3944 | 0.2604 | 0.0499 | 0.0435* |
| MK vs. summed linear acceleration | 0.0442 | 0.3239 | 0.2382 | 0.0181 | 0.0555 |
| K axial vs. summed linear acceleration | 0.0617 | 0.2420 | 0.2143 | 0.0421 | 0.0714 |
| K radial vs. summed linear acceleration | 0.0363 | 0.3724 | 0.2766 | 0.0148 | 0.0362* |
| MK vs. summed rotational acceleration | 0.0507 | 0.2899 | 0.2409 | 0.0174 | 0.0539 |
| K axial vs. summed rotational acceleration | 0.0693 | 0.2141 | 0.2193 | 0.0447 | 0.0678 |
| K radial vs. summed rotational acceleration | 0.0419 | 0.3374 | 0.2778 | 0.0117 | 0.0357* |
p < 0.05. Bold p values.
HITS, Head Impact Telemetry System; DKI, diffusional kurtosis imaging; SD, standard deviation; BMI, body mass index; MK, mean kurtosis; RWEcp, Risk Weighted Cumulative Exposure combined probability; K axial, axial kurtosis; K radial, radial kurtosis.
Table 3A.
Associations Between HITS Metrics and Changes in WMM Metrics in White Matter Areas With FA >0.4 (<−2SD)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| AWF vs. RWECP | 0.0488 | 0.2994 | 0.0343 | 0.1321 | 0.3415 |
| Tortuosity vs. RWECP | 0.1462 | 0.0652 | 0.1504 | 0.2696 | 0.1327 |
| De axial vs. RWECP | 0.0854 | 0.1659 | 0.1082 | 0.1638 | 0.1921 |
| De radial vs. RWECP | 0.1051 | 0.1222 | 0.4687 | 0.3756 | 0.0025* |
| Da vs. RWECP | 0.1093 | 0.1146 | 0.1823 | 0.2421 | 0.0983 |
| AWF vs. RWELinear | 0.0847 | 0.1676 | 0.0903 | 0.1825 | 0.2227 |
| Tort vs. RWELinear | 0.0631 | 0.2364 | 0.0010 | 0.1487 | 0.4046 |
| De axial vs. RWELinear | 0.0475 | 0.3062 | 0.0786 | 0.1360 | 0.2447 |
| De radial vs. RWELinear | 0.0260 | 0.4517 | 0.4298 | 0.3299 | 0.0047* |
| Da vs. RWELinear | 0.1053 | 0.1219 | 0.1745 | 0.2349 | 0.1059 |
| AWF vs. RWERotational | 0.3069 | 0.0050* | 0.3562 | 0.4215 | 0.0135* |
| Tortuosity vs. RWERotational | 0.1205 | 0.0965 | 0.0358 | 0.1710 | 0.3378 |
| De axial vs. RWERotational | 0.0030 | 0.7997 | 0.0209 | 0.0819 | 0.3752 |
| De radial vs. RWERotational | 0.0005 | 0.9213 | 0.3036 | 0.1816 | 0.0264* |
| Da vs. RWERotational | 0.0469 | 0.3094 | 0.0402 | 0.1105 | 0.3271 |
| AWF vs. Total Impacts | 0.0973 | 0.1379 | 0.0141 | 0.1140 | 0.3932 |
| Tortuosity vs. Total Impacts | 0.0166 | 0.5485 | −0.1297 | 0.0287 | 0.8478 |
| De axial vs. Total Impacts | 0.0106 | 0.6314 | −0.0018 | 0.0607 | 0.4369 |
| De radial vs. Total Impacts | 0.0014 | 0.8621 | 0.2599 | 0.1302 | 0.0438* |
| Da vs. Total Impacts | 0.0708 | 0.2087 | 0.0362 | 0.1067 | 0.3368 |
| AWF vs. summed linear acceleration | 0.1128 | 0.1086 | 0.0628 | 0.1699 | 0.2766 |
| Tortuosity vs. summed linear acceleration | 0.0242 | 0.4684 | −0.1063 | 0.0813 | 0.7730 |
| De axial vs. summed linear acceleration | 0.0107 | 0.6309 | 0.0057 | 0.1083 | 0.4160 |
| De radial vs. summed linear acceleration | 0.0001 | 0.9712 | 0.2986 | 0.3412 | 0.0280* |
| Da vs. summed linear acceleration | 0.0414 | 0.1720 | 0.0817 | 0.1743 | 0.2387 |
| AWF vs. summed rotational acceleration | 0.0885 | 0.1580 | 0.0214 | 0.1262 | 0.3740 |
| Tortuosity vs. summed rotational acceleration | 0.0196 | 0.5138 | −0.1175 | 0.0514 | 0.8095 |
| De axial vs. summed rotational acceleration | 0.0073 | 0.6912 | −0.0064 | 0.0910 | 0.4502 |
| De radial vs. summed rotational acceleration | 0.0001 | 0.9928 | 0.2934 | 0.3265 | 0.0298* |
| Da vs. summed rotational acceleration | 0.0738 | 0.1990 | 0.0662 | 0.1587 | 0.2694 |
p < 0.05. Bold p values.
HITS, Head Impact Telemetry System; WMM, white matter modeling; FA, fractional anisotropy; SD, standard deviation; BMI, body mass index; AWF, axonal water fraction; RWEcp, Risk Weighted Cumulative Exposure combined probability; De axial and radial, extra-axonal diffusivity; Da, intra-axonal diffusivity.
Table 3B.
Associations Between HITS Metrics and Changes in DKI-Derived Metrics in Whole–Brain (< −2 SD)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| MK vs. RWECP | 0.0004 | 0.9282 | 0.1101 | 0.0338 | 0.1891 |
| K axial vs. RWECP | 0.0008 | 0.8971 | 0.0808 | 0.0114 | 0.2404 |
| K radial vs. RWECP | 0.0127 | 0.5995 | 0.1919 | 0.0898 | 0.0895 |
| MK vs. RWELinear | 0.0014 | 0.8618 | 0.1327 | 0.0584 | 0.1555 |
| K axial vs. RWELinear | 0.0062 | 0.7156 | 0.0983 | 0.0302 | 0.2087 |
| K radial vs. RWELinear | 0.0001 | 0.9601 | 0.2006 | 0.0997 | 0.0820 |
| MK vs. RWERotational | 0.0264 | 0.4480 | 0.3915 | 0.3393 | 0.0083* |
| K axial vs. RWERotational | 0.0024 | 0.8216 | 0.2380 | 0.1806 | 0.0556 |
| K radial vs. RWERotational | 0.0205 | 0.5043 | 0.4340 | 0.3625 | 0.0044* |
| MK vs. total impacts | 0.0085 | 0.6683 | 0.1209 | 0.0456 | 0.1723 |
| K axial vs. total impacts | 0.0187 | 0.5235 | 0.0930 | 0.0245 | 0.2181 |
| K radial vs. total impacts | 0.0068 | 0.7018 | 0.1711 | 0.0664 | 0.1094 |
| MK vs. summed linear acceleration | 0.0075 | 0.6874 | 0.1309 | 0.1383 | 0.1580 |
| K axial vs. summed linear acceleration | 0.0176 | 0.5371 | 0.0984 | 0.0828 | 0.2084 |
| K radial vs. summed linear acceleration | 0.0058 | 0.7243 | 0.1818 | 0.1823 | 0.0988 |
| MK vs. summed rotational acceleration | 0.0084 | 0.6695 | 0.1222 | 0.1166 | 0.1703 |
| K axial vs. summed rotational acceleration | 0.0188 | 0.5233 | 0.0926 | 0.0654 | 0.2186 |
| K radial vs. summed rotational acceleration | 0.0056 | 0.7277 | 0.1751 | 0.1648 | 0.1053 |
p < 0.05. Bold p values.
HITS, Head Impact Telemetry System; DKI, diffusional kurtosis imaging; SD, standard deviation; BMI, body mass index; MK, mean kurtosis; RWEcp, Risk Weighted Cumulative Exposure combined probability; K axial, axial kurtosis; K radial, radial kurtosis.
Table 3C.
Associations Between HITS Metrics and Changes in DKI-Derived Metrics in White Matter (< −2 SD)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| MK vs. RWECP | 0.0115 | 0.6179 | 0.0537 | 0.0909 | 0.2964 |
| K axial vs. RWECP | 0.0456 | 0.3163 | 0.2406 | 0.2192 | 0.0541 |
| K radial vs. RWECP | 0.1474 | 0.0640 | 0.4024 | 0.4194 | 0.0071* |
| MK vs. RWELinear | 0.0283 | 0.4317 | 0.1227 | 0.1572 | 0.1697 |
| K axial vs. RWELinear | 0.0307 | 0.4129 | 0.2750 | 0.2545 | 0.0369* |
| K radial vs. RWELinear | 0.0443 | 0.3233 | 0.2057 | 0.2283 | 0.0779 |
| MK vs. RWERotational | 0.2378 | 0.0156* | 0.4957 | 0.5155 | 0.0016* |
| K axial vs. RWERotational | 0.0352 | 0.3799 | 0.2230 | 0.2011 | 0.0652 |
| K radial vs. RWERotational | 0.0612 | 0.2438 | 0.0713 | 0.0977 | 0.2590 |
| MK vs. total impacts | 0.0581 | 0.2564 | 0.1115 | 0.1464 | 0.1868 |
| K axial vs. total impacts | 0.0104 | 0.6354 | 0.1443 | 0.1201 | 0.1402 |
| K radial vs. total impacts | 0.0128 | 0.5984 | 0.0253 | 0.0530 | 0.3640 |
| MK vs. summed linear acceleration | 0.0578 | 0.2578 | 0.1418 | 0.2425 | 0.1435 |
| K axial vs. summed linear acceleration | 0.0144 | 0.5770 | 0.1873 | 0.2767 | 0.0936 |
| K radial vs. summed linear acceleration | 0.0170 | 0.5441 | 0.0554 | 0.1288 | 0.2926 |
| MK vs. summed rotational acceleration | 0.0466 | 0.3109 | 0.1113 | 0.2044 | 0.1872 |
| K axial vs. summed rotational acceleration | 0.0097 | 0.6464 | 0.1577 | 0.2323 | 0.1240 |
| K radial vs. summed rotational acceleration | 0.0197 | 0.5129 | 0.0572 | 0.1279 | 0.2886 |
p < 0.05. Bold p values.
HITS, Head Impact Telemetry System; DKI, diffusional kurtosis imaging; SD, standard deviation; BMI, body mass index; MK, mean kurtosis; RWEcp, Risk Weighted Cumulative Exposure combined probability; K axial, axial kurtosis; K radial, radial kurtosis.
Table 3D.
Associations Between HITS Metrics and Changes in DKI-Derived Metrics in Gray Matter (< −2 SD)
| Without covariate adjustment | Covariate adjustment for age, BMI, and time between scans | ||||
|---|---|---|---|---|---|
| R2 | p value | Adjusted R2 | Covariate-adjusted R2 | p value | |
| MK vs. RWECP | 0.0001 | 0.9570 | 0.1327 | 0.0282 | 0.1555 |
| K axial vs. RWECP | 0.0020 | 0.8363 | 0.0654 | 0.0052 | 0.2712 |
| K radial vs. RWECP | 0.0094 | 0.6521 | 0.2139 | 0.0782 | 0.0717 |
| MK vs. RWELinear | 0.0047 | 0.7514 | 0.1466 | 0.0438 | 0.1373 |
| K axial vs. RWELinear | 0.0094 | 0.6518 | 0.0775 | 0.0181 | 0.2468 |
| K radial vs. RWELinear | 0.0005 | 0.9149 | 0.2153 | 0.0798 | 0.0707 |
| MK vs. RWERotational | 0.0106 | 0.6321 | 0.3648 | 0.2883 | 0.0121* |
| K axial vs. RWERotational | 0.0011 | 0.8801 | 0.2135 | 0.1628 | 0.0720 |
| K radial vs. RWERotational | 0.0079 | 0.6787 | 0.4205 | 0.3205 | 0.0054* |
| MK vs. total impacts | 0.0220 | 0.4890 | 0.1326 | 0.0281 | 0.1557 |
| K axial vs. total impacts | 0.0250 | 0.4604 | 0.0746 | 0.0151 | 0.2524 |
| K radial vs. total impacts | 0.0185 | 0.5268 | 0.1860 | 0.0455 | 0.0948 |
| MK vs. summed linear acceleration | 0.0199 | 0.5107 | 0.1399 | 0.0978 | 0.1459 |
| K axial vs. summed linear acceleration | 0.0236 | 0.4735 | 0.0784 | 0.0525 | 0.2449 |
| K radial vs. summed linear acceleration | 0.0167 | 0.5468 | 0.1937 | 0.1383 | 0.0879 |
| MK vs. summed rotational acceleration | 0.0203 | 0.5068 | 0.1347 | 0.0815 | 0.1528 |
| K axial vs. summed rotational acceleration | 0.0247 | 0.4633 | 0.0744 | 0.0387 | 0.2529 |
| K radial vs. summed rotational acceleration | 0.0157 | 0.5590 | 0.1898 | 0.1256 | 0.0913 |
p < 0.05. Bold p values.
HITS, Head Impact Telemetry System; DKI, diffusional kurtosis imaging; SD, standard deviation; BMI, body mass index; MK, mean kurtosis; RWEcp, Risk Weighted Cumulative Exposure combined probability; K axial, axial kurtosis; K radial, radial kurtosis.
When only increases in MK (whole–brain) were considered (Table 2B), the relationships were similar to when both ends of the distribution were considered. The relationship between MK and RWECP explained 9.4% of the variance (p = 0.1446). After covariate adjustment, this relationship increased to explain 46.3% of the variance (p = 0.0028). The relationship between AWF and RWECP explained 21.3% of the variance (p = 0.0232), which increased after covariate adjustment to 39.4% of the variance (p = 0.0081).
When examining only decreases (Tables 3A-D), the relationship between MK and RWECP did not achieve significance. However, De radial was significant following covariate adjustment, as well as K radial in the WM. Similarly, for RWElinear, only De axial and K axial in the white matter achieved significance following covariate adjustment. Interestingly, multiple metrics achieved significance for the rotational component (RWErotational), including AWF, De radial, MK, and K radial.
Total impacts
DKI-derived metrics, (MK, K axial, and K radial), compared with total impacts achieved significance only after covariate adjustment. For the WMM, De radial versus Total Impacts achieved significance when examining the decreases in white matter areas with FA >0.4. Other WMM metrics (AWF, tortuosity, De axial, and Da) did not achieve a significant relationship, compared with total impacts.
Summed acceleration
DKI-derived metrics, (MK, K axial, and K radial), compared with summed linear acceleration, as well as summed rotational acceleration, achieved significance in gray matter and whole–brain only after covariate adjustment. Similar to total impacts, De radial versus summed linear acceleration and De radial versus summed rotational acceleration achieved significance when examining the decreases in white matter areas with FA >0.4. Other WMM metrics (AWF, tortuosity, De axial, and Da) did not achieve a significant relationship, compared with summed linear acceleration or summed rotational acceleration.
Cognitive testing
Spearman's rank correlation revealed no statistically significant associations between ImPACT composite score decrease (post- minus pre-season) and the number of abnormal voxels.
Discussion
In this study, we compared the pre- and post-season imaging data and cognitive data of players with head impact exposure experienced during one season of high school football, represented by RWE. A method was used allowing the number of abnormal DKI-derived metric voxels to be measured independent of spatial relationships. The number of abnormal voxels (> 2 SD) in all DKI-derived and most WMM metrics had a statistically significant association with RWECP. This study uses the same subjects and biomechanical data as a previous report investigating relationships between DTI-derived metrics and head impacts, allowing for direct comparison with the DTI data.11 These studies are among the first to report quantitative relationships between head impact metrics and DTI-derived or DKI-derived scalars in non-concussed subjects.
The RWE metric captures the wide variances in exposure within the subjects. RWECP takes into account both the frequency and severity of the peak linear and rotational acceleration experienced from each impact to the head. RWELinear and RWERotational are computed from the peak linear and rotational accelerations separately. Each are computed from the respective risk function (combined probability, linear, or rotational). A positive relationship between an increasing RWE metric and an increasing number of abnormal DKI-derived and WMM metric voxels suggests an association between increased cumulative head impact exposure and white matter integrity changes. Studies in animal models and humans have shown the risk of brain injury and associated functional impairment increases as the frequency and severity of head impacts increase.35–37 There are few studies relating DKI-derived or WMM metrics to TBI, or mTBI. However, it has been shown that DKI-derived metrics change in the presence of mTBI, especially MK.21 Here, we demonstrate changes in DKI-derived and WMM metrics that are significantly associated with an athlete's cumulative head impact exposure, represented as RWECP, in the absence of clinically diagnosed concussion.
RWECP was able to explain variance in all DKI-derived and most WMM metrics. RWELinear was able to explain the variance in fewer metrics than those explained by RWECP. DKI-derived scalars demonstrated limited significant relationships with RWERotational, total impacts, or summed acceleration. We previously found that DTI-derived metrics were better explained by RWECP and demonstrated no relationship with total number of impacts.11 RWE is an equation that includes not only the number of impacts or total acceleration, but the summed risk associated with the rotational and linear acceleration of each impact. The number of impacts or acceleration alone provide partial information, as the frequency and severity of impacts may have difference effects. RWE considers the non-linear relationship between impact magnitude and concussion risk and may be a more robust metric of characterizing the cumulative exposure of an athlete. Our findings with DKI metrics, again, suggest that knowledge of the cumulative exposure of an athlete, represented by both the frequency and severity (linear and rotational acceleration) of each impact, is needed for accurate characterization of the effects of sub-concussive head impacts.
Changes in WMM metrics and DKI-derived metrics with regard to RWE may provide more information on the response of white matter to mTBI and subconcussive impacts. Water diffuses through biological tissues in a non-Gaussian manner due to cellular microstructure. This is also seen in the brain, especially due to myelinated axons. A higher mean kurtosis indicates more microstructural complexity. The axial and radial kurtosis provide the direction of any potential abnormalities. Tortuosity represents the ratio of diffusion along the direction of the fibers to diffusion perpendicular to the fibers in the EAS. Thus, tortuosity is a measure of the packing arrangement of the axons, not simply the packing density.19 AWF represents the fraction of water signal in the axons relative to the total water signal. AWF values are comparable to axonal volume density measures in animal models.34 De radial is expected to be sensitive to axonal volume, as well as myelin integrity. The De axial and Da metrics should be sensitive to structural changes along, or parallel, the axon (e.g. axonal beading).38
In our study, we observed a significant relationship between cumulative exposure metrics and many of the DKI-derived and WMM metrics. These results indicate a variety of changes and injury types that may be occurring within the white matter, including axonal swelling, axonal beading, ischemia, and astrogliosis. Increases in AWF, indicating a greater amount of water in the axons relative to the total water signal post-season than pre-season, are indicative of axonal swelling. MK, K axial, and K radial all increased significantly for whole–brain, white matter, and gray matter. Similar changes have been seen previously in ischemic regions of stroke patients.38,39 The significant increase in MK also has been demonstrated in axonal injury and astrogliosis.25 Astrogliosis is the increase of reactive astrocytes due to the destruction of nearby neurons. This abnormal increase in astrocytes increases the microcellular complexity and has been shown to significantly elevate the measured MK in animal models.25 The increase in astrocytes is a lingering effect seen in animal models after induced TBI.40 Axonal injury and the associated release of cytokines by activated microglia can induce astrogliosis. Microglial inhibition is now the target of several potential and promising TBI therapies.41–43
Both significant increases and decreases were seen in the various WMM metrics. The trending decrease in Da, in conjunction with the increase in AWF, follows a model of ischemia and is consistent with axonal beading.38 The increases in Da with decreases in De radial suggest areas of cytotoxic edema, causing water to shift from extra- to intra-axonal regions. In contrast, the increases in De axial and radial may be due to areas of extra-axonal inflammation or vasogenic edema. Interestingly, none of the results were suggestive of demyelination. In summary, our findings indicate that the axons are experiencing a variety of changes in their microstructural complexity. This may be indicative of multiple mechanisms, including swelling, beading, ischemia, and astrogliosis. However, the pathological implications of these metrics still are not well understood.
In all of these relationships, it is important to consider the strong effect of the covariates. DKI-derived metrics have proven to be a strong predictor of brain maturation, where DTI-derived metrics showed little dependency on age.44,45 The DKI-derived metrics could be especially sensitive to the brain changes due to age and time between scans, making them important factors to regress out. However, the effect of BMI on DKI-derived metrics has not been well studied. There is evidence suggesting an effect of BMI on DTI-derived metrics.46 A study of well characterized healthy children and animal models is necessary to further investigate these relationships.
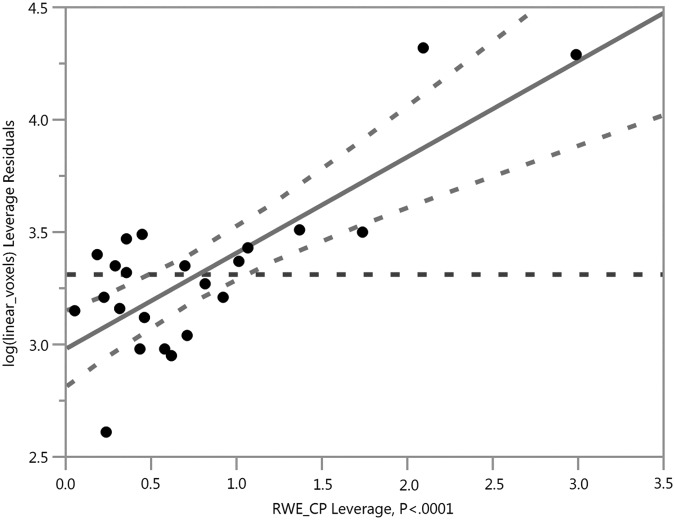
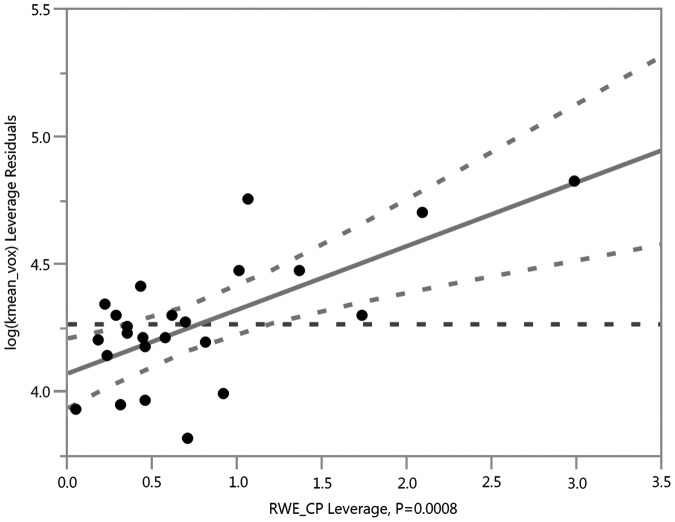
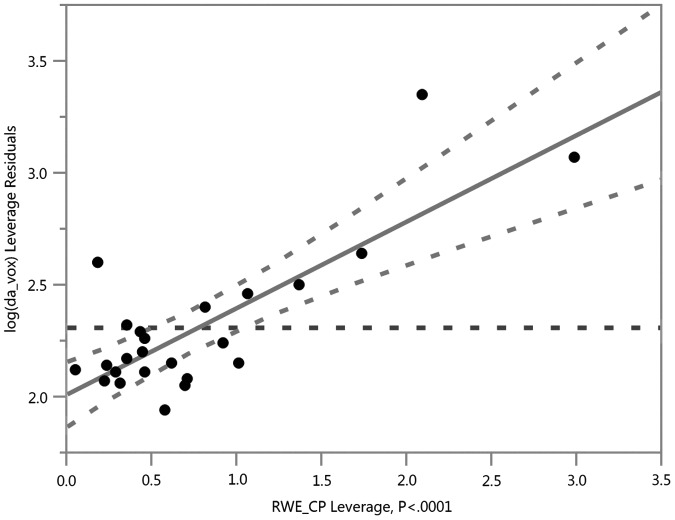
In comparison to a previous study of DTI-derived metrics (obtained at the same imaging sessions in this exact same cohort), the DKI-derived scalar relationships with RWE explained more variance—especially Da, MK, K axial, and K radial—in whole–brain and gray matter, suggesting that DKI may provide more sensitive and specific metrics for subconcussive head impacts. Our previous work with DTI in this group demonstrated the strongest relationship between linear anisotropy (CL) and RWECP (R2 = 0.5626; p < 0.0001), as shown in Figure 1. In the current study, the strongest relationships were between MK and RWECP (R2 = 0.6598; p < 0.0001), as well as Da and RWECP (R2 = 0.6412; p < 0.0001), as shown in Figures 2 and 3. The relationship with CL in our previous study suggested axotomy, or axonal tearing. The changes in Da demonstrated here, however, are more suggestive of axonal beading and cytotoxic edema. The previous study demonstrated increases in spherical and planar diffusivities suggestive of demyelination. In contrast, we did not demonstrate evidence of demyelination in the DKI-derived metrics. This is not necessarily conflicting, as the DKI-derived metrics are more specific and can provide less ambiguous information. In addition, the relationship with MK and RWECP was suggestive of astrogliosis.
FIG. 1.
Risk Weighted Cumulative Exposure combined probability (RWECP) vs. abnormal linear anisotropy (CL) voxels in the white matter, adjusted for age, body mass index, and time between scans (R2 = 0.5626; p < 0.0001).
FIG. 2.
Risk Weighted Cumulative Exposure combined probability (RWECP) vs. abnormal kurtosis (K) mean voxels in the whole–brain, adjusted for age, body mass index, and time between scans (R2 = 0.6598; p < 0.0001).
FIG. 3.
Risk Weighted Cumulative Exposure combined probability (RWECP) vs. abnormal intra-axonal diffusivity (Da) voxels in white matter areas with fractional anisotropy (FA) >0.4, adjusted for age, body mass index, and time between scans (R2 = 0.6412; p < 0.0001).
We found no statistically significant relationships between magnitude of delta ImPACT composite scores (post- minus pre-season) and number of abnormal voxels for any imaging metrics. We did demonstrate a significant relationship between Verbal Memory composite score and DTI metrics in our previous study.11 It is known that DKI-derived metrics relate to cognitive metrics in Alzheimer's disease and mild cognitive impairment.47 To identify this relationship in our cohort, a larger sample may be needed. In addition, the ImPACT test has proven sensitive to concussion, but its sensitivity to sub-concussive cognitive changes is unknown and the statistical power to detect associations may have been low.48 The DKI metrics also may be demonstrating changes taking place in the brain before they become clinically apparent. This phenomena of the discrepancy between the amount of brain damage and the observed clinical manifestations is often described as cognitive reserve.49
Several caveats must be considered. Our sample size is relatively small; however, it is one of the largest studies to date of non-concussed high school football players to include biomechanics, imaging, and cognitive data. Our subjects were monitored during all practices and games by trained staff in concussion identification and management, including a certified athletic trainer. However, it is possible a concussion was not reported or went undetected, as previous studies show a 50% underreporting rate for concussion in high school football.50 Although a control group of non-contact sport athletes was not used, this is somewhat mitigated by the use of delta metrics with the subjects baseline scans serving as an internal control. Our study was not designed to examine the potential reversibility or the time course of these changes. The WMM parameters are based on specific tissue modeling assumptions,51 and so their interpretation should be regarded as preliminary.
Conclusion
We demonstrate a significant relationship between changes in DKI-derived metrics and cumulative head impact exposure using the RWE metric in the absence of clinical concussion. In this study, we show that a single season of high school football produced DKI-derived and WMM metric changes that have previously been seen in animal models of TBI. Although the pathophysiologic implications of these metrics will still require further research, this study adds to a growing body of literature demonstrating that a single season of contact sports can result in brain changes regardless of clinical findings or concussion diagnosis.
Acknowledgments
The authors would like to thank the Reagan High School, especially Ashley Lake, ATC, Corbin Ratcliffe, Lauren Smith, and the football program. Thank you to Ben Wagner and all those who contributed to the study development. Special thanks to the Childress Institute for Pediatric Trauma at Wake Forest Baptist Medical Center for providing support for this study. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-0907738. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors(s) and do not necessarily reflect the views of the National Science Foundation. Support for this research also was provided by National Institutes of Health grant NS082453 (JAM,JDS), NS088125 (JAM), and R01NS091602 (CTW, JAM, JDS).
References
- 1.Marar M., McIlvain N.M., Fields S.K., and Comstock R.D. (2012). Epidemiology of concussions among United States high school athletes in 20 sports. Am. J. Sports Med. 40, 747–755 [DOI] [PubMed] [Google Scholar]
- 2.OTL: Pop Warner participation drops. Available at: http://espn.go.com/espn/otl/story/_/page/popwarner/pop-warner-youth-football-participation-drops-nfl-concussion-crisis-seen-causal-factor Accessed April20, 2016
- 3.Brolinson P.G., Manoogian S., McNeely D., Goforth M., Greenwald R., and Duma S. (2006). Analysis of linear head accelerations from collegiate football impacts. Curr. Sports Med. Rep. 5, 23–28 [DOI] [PubMed] [Google Scholar]
- 4.Duma S.M., Manoogian S.J., Bussone W.R., Brolinson P.G., Goforth M.W., Donnenwerth J.J., Greenwald R.M., Chu J.J., and Crisco J.J. (2005). Analysis of real-time head accelerations in collegiate football players. Clin. J. Sport Med. 15, 3–8 [DOI] [PubMed] [Google Scholar]
- 5.Schnebel B., Gwin J.T., Anderson S., and Gatlin R. (2007). In vivo study of head impacts in football: a comparison of National Collegiate Athletic Association Division I versus high school impacts. Neurosurgery 60, 490–495 [DOI] [PubMed] [Google Scholar]
- 6.Guskiewicz K.M., Mihalik J.P., Shankar V., Marshall S.W., Crowell D.H., Oliaro S.M., Ciocca M.F., and Hooker D.N. (2007). Measurement of head impacts in collegiate football players: relationship between head impact biomechanics and acute clinical outcome after concussion. Neurosurgery 61, 1244–1252 [DOI] [PubMed] [Google Scholar]
- 7.Urban J.E., Davenport E.M., Golman A.J., Maldjian J.A., Whitlow C.T., Powers A.K., and Stitzel J.D. (2013). Head impact exposure in youth football: high school ages 14 to 18 years and cumulative impact analysis. Ann. Biomed. Eng. 41, 2474–2487 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cobb B.R., Urban J.E., Davenport E.M., Rowson S., Duma S.M., Maldjian J.A., Whitlow C.T., Powers A.K., and Stitzel J.D. (2013). Head impact exposure in youth football: elementary school ages 9–12 years and the effect of practice structure. Ann. Biomed. Eng. 41, 2463–2473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wong R.H., Wong A.K., and Bailes J.E. (2014). Frequency, magnitude, and distribution of head impacts in Pop Warner football: the cumulative burden. Clin. Neurol. Neurosurg. 118, 1–4 [DOI] [PubMed] [Google Scholar]
- 10.Mills K.L. and Tamnes C.K. (2014). Methods and considerations for longitudinal structural brain imaging analysis across development. Dev. Cogn. Neurosci. 9, 172–190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Davenport E.M., Whitlow C.T., Urban J.E., Espeland M.A., Jung Y., Rosenbaum D.A., Gioia G.A., Powers A.K., Stitzel J.D., and Maldjian J.A. (2014). Abnormal white matter integrity related to head impact exposure in a season of high school varsity football. J. Neurotrauma 31, 1617–1624 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bazarian J.J., Zhu T., Zhong J., Janigro D., Rozen E., Roberts A., Javien H., Merchant-Borna K., Abar B., and Blackman E.G. (2014). Persistent, long-term cerebral white matter changes after sports-related repetitive head impacts. PLoS One 9, e94734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.DeCarlo L.T. (1997). On the meaning and use of kurtosis. Psychol. Methods 2, 292–307 [Google Scholar]
- 14.Jensen J.H., and Helpern J.A. (2010). MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 23, 698–710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jensen J.H., Helpern J.A., Ramani A., Lu H., and Kaczynski K. (2005). Diffusional kurtosis imaging: The quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med. 53, 1432–1440 [DOI] [PubMed] [Google Scholar]
- 16.Jensen J.H. and Helpern J.A. (2010). MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 23, 698–710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lazar M. (2010). Mapping brain anatomical connectivity using white matter tractography. NMR Biomed. 23, 821–835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hui E.S., Russell Glenn G., Helpern J.A., and Jensen J.H. (2015). Kurtosis analysis of neural diffusion organization. NeuroImage 106, 391–403 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jelescu I.O., Veraart J., Adisetiyo V., Milla S.S., Novikov D.S., and Fieremans E. (2015). One diffusion acquisition and different white matter models: how does microstructure change in human early development based on WMTI and NODDI? NeuroImage 107, 242–256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lazar M., Miles L.M., Babb J.S., and Donaldson J.B. (2014). Axonal deficits in young adults with High Functioning Autism and their impact on processing speed. NeuroImage: Clin. 4, 417–425 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Stokum J.A., Sours C., Zhuo J., Kane R., Shanmuganathan K., and Gullapalli R.P. (2015). A longitudinal evaluation of diffusion kurtosis imaging in patients with mild traumatic brain injury. Brain Inj. 29, 47–57 [DOI] [PubMed] [Google Scholar]
- 22.Adisetiyo V., Tabesh A., Di Martino A., Falangola M.F., Castellanos F.X., Jensen J.H., and Helpern J.A. (2014). Attention-deficit/hyperactivity disorder without comorbidity is associated with distinct atypical patterns of cerebral microstructural development. Hum. Brain Mapp. 35, 2148–2162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fieremans E., Benitez A., Jensen J.H., Falangola M.F., Tabesh A., Deardorff R.L., Spampinato M.V.S., Babb J.S., Novikov D.S., Ferris S.H. and Helpern J.A. (2013). Novel white matter tract integrity metrics sensitive to Alzheimer disease progression. A.J.N.R. Am. J. Neuroradiol. 34, 2105–2112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Grossman E.J., Jensen J.H., Babb J.S., Chen Q., Tabesh A., Fieremans E., Xia D., Inglese M., and Grossman R.I. (2013). Cognitive impairment in mild traumatic brain injury: a longitudinal diffusional kurtosis and perfusion imaging study. A.J.N.R. Am. J. Neuroradiol. 34, 951–957, S951–953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhuo J., Xu S., Proctor J.L., Mullins R.J., Simon J.Z., Fiskum G., and Gullapalli R.P. (2012). Diffusion kurtosis as an in vivo imaging marker for reactive astrogliosis in traumatic brain injury. NeuroImage 59, 467–477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Broglio S.P., Sosnoff J.J., Shin S., He X., Alcaraz C., and Zimmerman J. (2009). Head impacts during high school football: a biomechanical assessment. J Athl Train 44, 342–349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Daniel R.W., Rowson S., and Duma S.M. (2012). Head impact exposure in youth football. Ann. Biomed. Eng. 40, 976–981 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rowson S. and Duma S.M. (2013). Brain injury prediction: assessing the combined probability of concussion using linear and rotational head acceleration. Ann. Biomed. Eng. 41, 873–882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rowson S., Duma S.M., Beckwith J.G., Chu J.J., Greenwald R.M., Crisco J.J., Brolinson P.G., Duhaime A.C., McAllister T.W., and Maerlender A.C. (2012). Rotational head kinematics in football impacts: an injury risk function for concussion. Ann. Biomed. Eng. 40, 1–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lovell M.R., M.W.C., Podell K., Powell J., Maroon J. (2000). ImPACT: Immediate Post-Concussion Assessment and Cognitive Testing. NeuroHealth Systems, LLC: Pittsburgh [Google Scholar]
- 31.Maroon J.C., Lovell M.R., Norwig J., Podell K., Powell J.W., and Hartl R. (2000). Cerebral concussion in athletes: evaluation and neuropsychological testing. Neurosurgery 47, 659–669 [DOI] [PubMed] [Google Scholar]
- 32.Smith S.M., Jenkinson M., Woolrich M.W., Beckmann C.F., Behrens T.E., Johansen-Berg H., Bannister P.R., De Luca M., Drobnjak I., Flitney D.E., Niazy R.K., Saunders J., Vickers J., Zhang Y., De Stefano N., Brady J.M., and Matthews P.M. (2004). Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage 23 Suppl 1, S208–S219 [DOI] [PubMed] [Google Scholar]
- 33.Tabesh A., Jensen J.H., Ardekani B.A., and Helpern J.A. (2011). Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magn. Reson. Med. 65, 823–836 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fieremans E., Jensen J.H., and Helpern J.A. (2011). White matter characterization with diffusional kurtosis imaging. NeuroImage 58, 177–188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ommaya A.K. and Hirsch A.E. (1971). Tolerances for cerebral concussion from head impact and whiplash in primates. J. Biomech. 4, 13–21 [DOI] [PubMed] [Google Scholar]
- 36.Ono K., Kikuchi A., Nakamura M., Kobayashi H., and Nakamura N. (1980). Human Head Tolerance to Sagittal Impact Reliable Estimation Deduced from Experimental Head Injury Using Subhuman Primates and Human Cadaver Skulls. SAE Technical Paper 801303 [Google Scholar]
- 37.Rowson S. and Duma S.M. (2013). Brain injury prediction: assessing the combined probability of concussion using linear and rotational head acceleration. Ann. Biomed. Eng. 41, 873–882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hui E.S., Fieremans E., Jensen J.H., Tabesh A., Feng W., Bonilha L., Spampinato M.V., Adams R., and Helpern J.A. (2012). Stroke assessment with diffusional kurtosis imaging. Stroke 43, 2968–2973 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jensen J.H., Falangola M.F., Hu C., Tabesh A., Rapalino O., Lo C., and Helpern J.A. (2011). Preliminary observations of increased diffusional kurtosis in human brain following recent cerebral infarction. NMR Biomed. 24, 452–457 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Shitaka Y., Tran H.T., Bennett R.E., Sanchez L., Levy M.A., Dikranian K., and Brody D.L. (2011). Repetitive closed-skull traumatic brain injury in mice causes persistent multifocal axonal injury and microglial reactivity. J. Neuropathol. Exp. Neurol. 70, 551–567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Giovanni S.D., Movsesyan V., Ahmed F., Cernak I., Schinelli S., Stoica B., and Faden A.I. (2005). Cell cycle inhibition provides neuroprotection and reduces glial proliferation and scar formation after traumatic brain injury. Proc. Natl. Acad. Sci. U.S.A. 102, 8333–8338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Erlich S., Alexandrovich A., Shohami E., and Pinkas-Kramarski R. (2007). Rapamycin is a neuroprotective treatment for traumatic brain injury. Neurobiol. Dis. 26, 86–93 [DOI] [PubMed] [Google Scholar]
- 43.Zhang D., Hu X., Qian L., O'Callaghan J.P., and Hong J.-S. (2010). Astrogliosis in CNS pathologies: is there a role for microglia? Mol. Neurobiol. 41, 232–241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Das S.K., Wang J.L., Bing L., Bhetuwal A., and Yang H.F. (2016). Regional values of diffusional kurtosis estimates in the healthy brain during normal aging. Clin. Neuroradiol. 2016. January 4; Epub ahead of print [DOI] [PubMed] [Google Scholar]
- 45.Cheung M.M., Hui E.S., Chan K.C., Helpern J.A., Qi L., and Wu E.X. (2009). Does diffusion kurtosis imaging lead to better neural tissue characterization? A rodent brain maturation study. Neuroimage 45, 386–392 [DOI] [PubMed] [Google Scholar]
- 46.Kullmann S., Callaghan M.F., Heni M., Weiskopf N., Scheffler K., Haring H.U., Fritsche A., Veit R., and Preissl H. (2016). Specific white matter tissue microstructure changes associated with obesity. Neuroimage 125, 36–44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Benitez A., Fieremans E., Jensen J.H., Falangola M.F., Tabesh A., Ferris S.H., and Helpern J.A. (2014). White matter tract integrity metrics reflect the vulnerability of late-myelinating tracts in Alzheimer's disease. NeuroImage Clin. 4, 64–71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Schatz P. and Sandel N. (2013). Sensitivity and specificity of the online version of ImPACT in high school and collegiate athletes. Am. J. Sports Med. 41, 321–326 [DOI] [PubMed] [Google Scholar]
- 49.Stern Y. (2009). Cognitive reserve. Neuropsychologia 47, 2015–2028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.McCrea M., Hammeke T., Olsen G., Leo P., and Guskiewicz K. (2004). Unreported concussion in high school football players: implications for prevention. Clin. J. Sports Med. 14, 13–17 [DOI] [PubMed] [Google Scholar]
- 51.Dhital B K.E., Reisert M, Kiselev VG. (2015). Isotropic Diffusion Weighting Provides Insight on Diffusion Compartments in Human Brain White Matter In vivo. In: ISMRM 23rd Annual Meeting & Exhibition. Proc. Intl. Soc. Mag. Reson. Med.: Toronto, Ontario, Canada, pps. 2788 [Google Scholar]