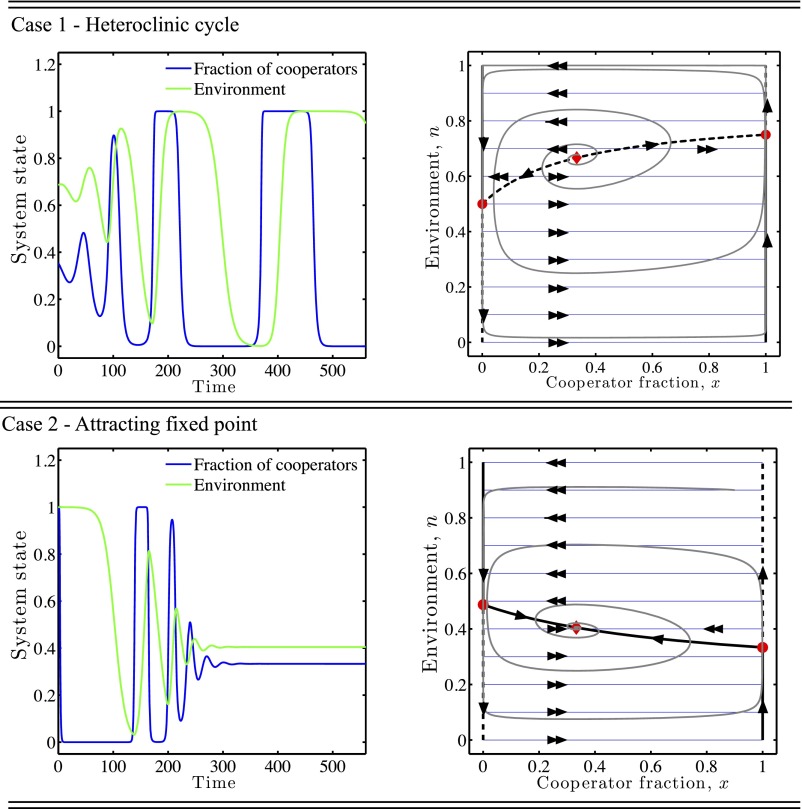
Fig. 3.

Fast–slow dynamics of feedback-evolving games, where x and n are the fast and slow variables, respectively—including critical manifolds and realized dynamics. In both panels, the black lines denote the critical manifolds with solid denoting attractors and dashed denoting repellers. The blue lines and double arrows denote expected fast dynamics in the limit $\mathrm{ϵ}\to 0$. The red circles denote the bifurcation points of the fast subsystem parameterized by n. The single arrows denote expected slow dynamics. The gray curve denotes the realized orbit. In both cases, $\mathrm{ϵ}=0.1$ and $\theta =2$. (Top) Relaxation oscillations converging to a heteroclinic cycle arising due to a saddle-node bifurcation in the fast subsystem parameterized by n in which the critical manifold is a repeller. The payoff matrix $A\left(n\right)$ is that defined in Eq. 21. (Bottom) Relaxation oscillations converging to a fixed point arising due to a saddle-node bifurcation in the fast subsystem parameterized by n in which the critical manifold is an attractor. The payoff matrix $A\left(n\right)$ is that defined in Eq. 23.