Reversible Leaf Xylem Collapse: A Potential “Circuit Breaker” against Cavitation^,

Reversible collapse of the xylem in the smallest vein orders of red oak leaves buffers major veins from cavitation over time scales relevant to stomatal responses.

Abstract

We report a novel form of xylem dysfunction in angiosperms: reversible collapse of the xylem conduits of the smallest vein orders that demarcate and intrusively irrigate the areoles of red oak (Quercus rubra) leaves. Cryo-scanning electron microscopy revealed gradual increases in collapse from approximately −2 MPa down to −3 MPa, saturating thereafter (to −4 MPa). Over this range, cavitation remained negligible in these veins. Imaging of rehydration experiments showed spatially variable recovery from collapse within 20 s and complete recovery after 2 min. More broadly, the patterns of deformation induced by desiccation in both mesophyll and xylem suggest that cell wall collapse is unlikely to depend solely on individual wall properties, as mechanical constraints imposed by neighbors appear to be important. From the perspective of equilibrium leaf water potentials, petioles, whose vessels extend into the major veins, showed a vulnerability to cavitation that overlapped in the water potential domain with both minor vein collapse and buckling (turgor loss) of the living cells. However, models of transpiration transients showed that minor vein collapse and mesophyll capacitance could effectively buffer major veins from cavitation over time scales relevant to the rectification of stomatal wrong-way responses. We suggest that, for angiosperms, whose subsidiary cells give up large volumes to allow large stomatal apertures at the cost of potentially large wrong-way responses, vein collapse could make an important contribution to these plants’ ability to transpire near the brink of cavitation-inducing water potentials.

Terrestrial photosynthesis is inextricably linked with water loss. Plants expose hydrated cells to the atmosphere to obtain CO₂, with evaporation an inevitable consequence. Vascular plants meet this challenge by replacing water lost via transpiration with water pulled from the soil. What allows this is the xylem: a system of stiff-walled conduits capable of remaining water filled at negative pressures low enough to extract water from micrometer- to nanometer-scale soil capillaries and to drive flow through the 10- to 100-μm-diameter xylem conduits that extend from the roots to the leaves (Tyree and Zimmermann, 2002). To deliver water at rates equal to transpiration, the pressure in the xylem must fall far below the vapor pressure of water, such that water transport through the xylem occurs in a metastable state (i.e. at kinetic, but not thermodynamic, equilibrium) and thus at risk of cavitation (Stroock et al., 2014). How many plants seemingly operate with little to no safety margin against cavitation (Brodribb et al., 2003; Brodribb and Holbrook, 2004; Meinzer et al., 2009; Choat et al., 2012) remains an important and unsolved question.

Cavitation occurs when metastable liquid water is replaced by water vapor due to the expansion of a gas bubble nucleus, forming an embolism or air blockage: embolism disrupts water transport because tensions cannot be transmitted through gas. The most probable origin of such nuclei is thought to be gas bubbles pulled through a pit membrane from an adjacent, gas-filled conduit (Lens et al., 2013), and many studies have focused on the formation and propagation by air seeding of embolism as a key determinant of plant performance (Choat et al., 2012). However, negative pressures in xylem conduits can affect xylem function in other ways. If xylem conduits are unable to withstand the mechanical forces imposed by the negative pressure, they can deform or collapse inward, with the reduction in Poiseuille (or effective) radius markedly reducing the hydraulic conductance. Conduit deformation has been observed in tracheids of conifer leaves, most notably in transfusion tracheids, which supply water laterally from the vein to the photosynthetic cells (Cochard et al., 2004a; Brodribb and Holbrook, 2005; Zhang et al., 2014). In angiosperms, leaf xylem conduit thickness-to-span ratios (thought to be predictive of collapse) have been shown to correlate with resistance to the loss of hydraulic conductance as xylem tensions increase (Blackman et al., 2010), but no previous study has addressed whether xylem conduits in angiosperm leaves collapse as leaf water potentials (Ψ_L) decline.

Plants avoid negative pressures that cause cavitation by closing their stomata. But in angiosperms, the regulation of transpiration is complicated by a stomatal mechanism in which the achievement of large apertures, and thus high surface conductances, involves not just the swelling of guard cells but also the shrinkage of subsidiary cells (Franks and Farquhar, 2007). A consequence of this is that stomatal aperture does not passively track Ψ_L, and increases in transpiration lead initially to opening rather than closing (referred to as a wrong-way response [WWR]; Mott and Parkhurst, 1991). The combination of high stomatal conductances and WWR means that the variation in transpiration rate due to fluctuations in wind speed, humidity, and leaf temperature places angiosperms at risk of potentially damaging transient drops in Ψ_L.

Here, we examine what happens to xylem conduits in the highest order (i.e. smallest) veins as Ψ_L declines. As the terminal end of the transpiration stream, the highest order veins are where the most negative pressures will occur and, thus, where the risk of embolism formation should be greatest. It is also where the tissues surrounding xylem conduits provide the least mechanical reinforcement and, thus, the greatest possibility of buckling. We focus here on leaves of red oak (Quercus rubra), a canopy species whose increasing dominance is accelerating carbon sequestration in New England mixed deciduous forests (Urbanski et al., 2007). Our goal is to determine whether terminal xylem conduits cavitate or collapse and how this relates to losses in the conductivity of xylem in larger, upstream veins. Our motivation is the hypothesis that buckling due to negative pressure, if reversible, could provide a means to protect upstream xylem from cavitation during the time it takes for stomata to regain control of transpiration following a rapid increase in hydraulic demand.

RESULTS

Cryo-Scanning Electron Microscopy Imaging of Buckling and Collapse in Xylem Conduits

To investigate the fate of xylem conduits under negative pressure, we froze leaves from greater than 1-m-long branches dried to varying water potentials and imaged freeze-fractured cross sections approximately 3 mm in length using cryo-scanning electron microscopy (cryo-SEM). As we were focused on the minor veins, our samples excluded 1° and 2° major veins. The next-largest veins that form ribs of ground tissue that extend above the surface of the leaf (3° and some 4°) also are classified as major veins, and they have been shown to contain vessels as well as protoxylem in Populus spp. (Russin and Evert, 1984). Such veins did not form a clean fracture plane and so were not included in the analysis. The next level of organization (e.g. some 4° and 5° order veins) included the majority of areole-bounding veins, defined by their complete bundle sheath extensions to both epidermal surfaces. These generally fractured cleanly, and we refer to them as boundary-type veins. The remaining level of vascular organization constitutes the intrusive veins that extend into individual areoles and includes veins grading between those with bundle-sheath extension to the lower epidermis alone (6°) and those entirely embedded within mesophyll (7°), which we lump together as intrusive-type veins. The total population of boundary- and intrusive-type veins we will refer to as minor veins.

Out of 1,037 xylem conduits of intrusive veins imaged by cryo-SEM of freeze-fractured leaves, ranging from −0.3 to −3.9 MPa in water potential, we found none that were embolized (gas filled). Nor was embolism observed in any of the 2,001 boundary-type conduits in samples wetter than −3 MPa. Out of three samples ranging from −3.4 to −3.9 MPa, two boundary-type veins were found that contained a total of 10 embolized conduits, or 3.6% of the 277 conduits observed for this vein type in this water potential range. The overall size distribution (based on perimeter, which we assumed to be invariant with shape) for all 2,278 conduits measured was notably right skewed, with a long tail of both large and rare conduits (Supplemental Fig. S1).

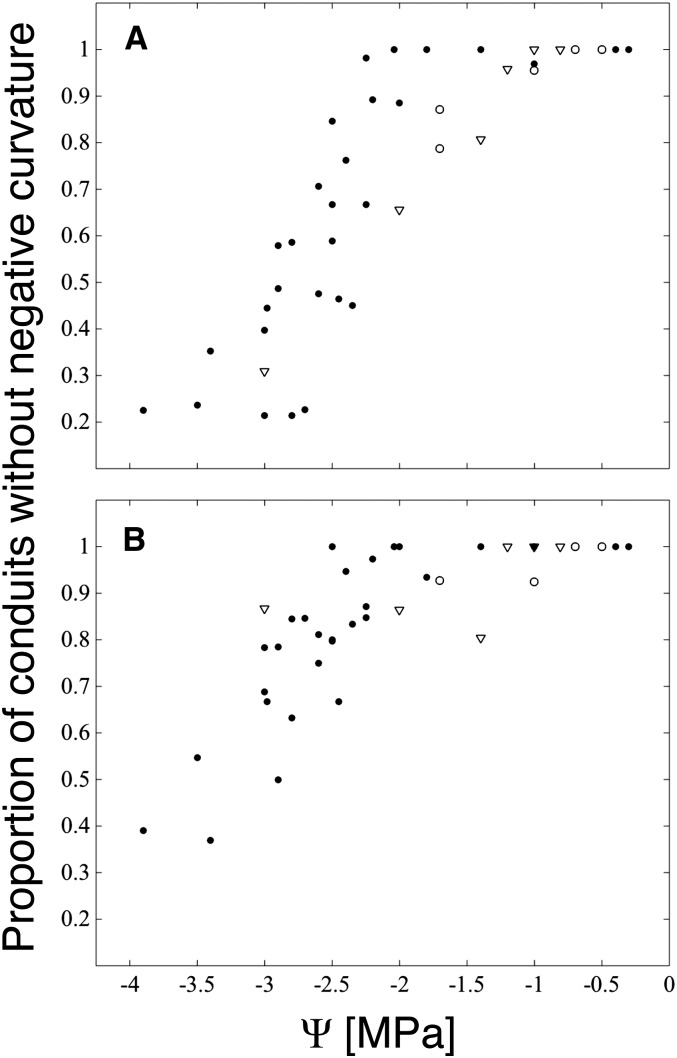
Rather than cavitate, as water potentials became drier than −2 MPa xylem conduits tended to become progressively more deformed (Fig. 1), as evidenced by declining HI (a measure of roundness; Fig. 2) and an increase in the frequency of conduits with negative (concave) curvature (Fig. 3). We interpret the appearance of negative curvature as indicating that a conduit has exceeded a threshold xylem tension for buckling, rather than as part of a conduit’s preferred, most often ovoid, stress-free shape. In the well-hydrated range for red oak (water potentials wetter than −1.5 MPa), no conduits were perfectly round (HI = 1), with HI ranging between 0.7 and 0.8 for both boundary- and intrusive-type veins (Fig. 2). In this same range, most samples lacked any conduits whose perimeters had one or more regions of negative curvature (Figs. 1A and 3).

Figure 1.

Freeze-fracture cryo-SEM images of the intrusive veins of red oak leaves. The hydraulic index (HI) of the xylem conduits, a measure of roundness, decreases as the water potential falls (bottom left corner). At −1 MPa (A), none of the xylem conduits show any negative curvature; by −2.5 MPa (B), two of the four conduits show signs of buckling (HI = 0.47 and 0.62); at −3 MPa (C), all conduits have buckled, but there is a broad range in the degree of deformation; by −3.5 MPa (D), most conduits are highly deformed (HI = 0.01, 0.03, 0.03, 0.2), while one (HI = 0.85) persists in an undeformed state. HI scores for each vein in total were as follows: 0.79 (A), 0.6 (B), 0.2 (C), and 0.05 (D).

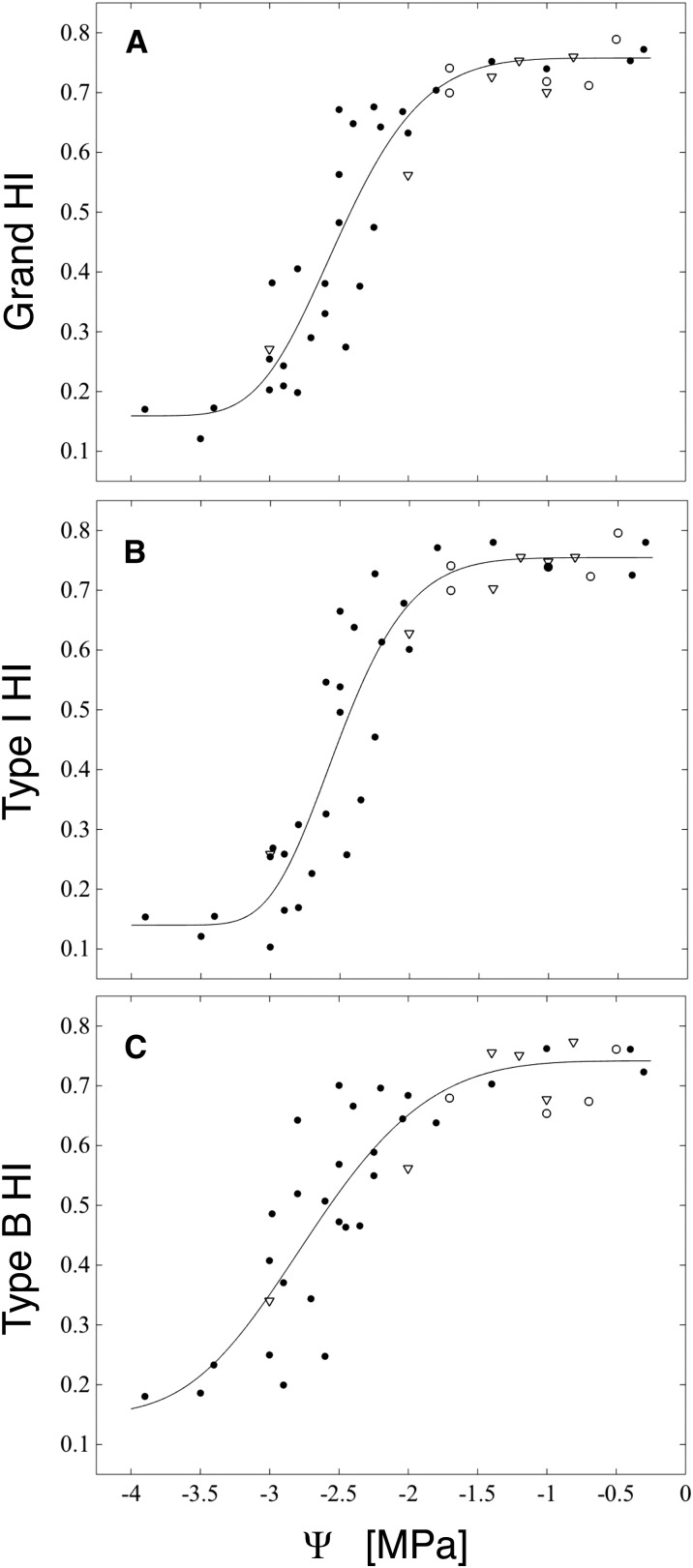
Figure 2.

Boundary and intrusive vein collapse as functions of water potential (Ψ). A, Grand HI for each leaf is calculated over all conduits from both vein types. B, Type I HI is calculated over all conduits from intrusive veins only. C, Type B HI is calculated over all conduits from boundary veins. HI scores for each leaf are plotted at the branch water potential (black circles) or for rehydrated leaves at the final equilibrium water potential (white circles; initial Ψ = −3.5 to −2.7) and at the predicted final equilibrium water potential for leaves frozen immediately after rehydration (white triangles; initial Ψ = −3.5 to −2.5 MPa).

Figure 3.

Proportion of conduits whose perimeters lack instances of negative (concave) curvature. A, Intrusive veins (type I). B, Boundary veins (type B). Scores for each leaf sample imaged are plotted at the parent branch water potential (black circles) or for rehydrated leaves at the final equilibrium water potential (white circles; initial Ψ = −3.5 to −2.7) and at the predicted final equilibrium water potential for leaves frozen immediately after rehydration (white triangles; initial Ψ = −3.5 to −2.5 MPa).

Following the appearance of negative curvature in a population of conduits, the degree of collapse observed increased as water potentials fell further (Figs. 1 and 2). That is, buckled conduits did not instantly (in the water potential domain) transition to very low (flattened) HI indices but rather appeared to resist further deformation (Fig. 1B). Nor did we find evidence of a bimodal distribution of HI scores in the range of water potentials over which collapse was occurring (Supplemental Figs. S2 and S3), as might be expected for a catastrophic, binary process. Larger conduits did appear to be more susceptible to deformation (Supplemental Fig. S3), and, as terminal xylem tracheids may be highly irregular in shape, we expect that the deformation of individual tracheids may vary along their length. Unfortunately, we were not able to fracture leaves in the plane tangential to the surface in order to view tracheids along their full length.

Rehydration prior to cryo-fixation showed that recovery from highly negative water potentials varied spatially and was consistent with an elastic (fast) response to changes in water potential. For example, in a leaf rehydrated from −3.5 MPa for 20 s and frozen, we observed heterogeneity in recovery of conduit shape across a fracture plane of only a few millimeters (Fig. 4, A and B). In this leaf, we further observed that the disposition of the mesophyll appeared to be under strong local control of the xylem: regions where xylem conduits remained distorted also were characterized by folded and deformed mesophyll (Fig. 4A), while in others, intrusive vein xylem had rerounded and the mesophyll appeared to have regained turgor (Fig. 4B). However, uptake of water for 2 min prior to cryo-fixation was sufficient for uniform recovery from −3.4 MPa (Fig. 4, C and D), and in general, we found no evidence of important levels of hysteresis in conduit shape as measured by HI following rehydration to equilibrium potentials wetter than −2 MPa (Fig. 2). However, the incidence of negative curvature did not always fully recover to zero (Figs. 3 and 4C), so some degree of plastic, or in the transient experiments (in which leaves were frozen after a short rehydration period) perhaps viscoelastic, deformation cannot be ruled out.

Figure 4.

Freeze-fracture cryo-SEM images of intrusive vein xylem recovery from deformation during rehydration. HI index scores are given for each conduit. In a leaf initially at −3.5 MPa and frozen after 20 s of hydration (A and B), the degree of recovery varies between different intrusive veins from no apparent recovery (A) with shrunken mesophyll to almost full recovery (B) with turgid mesophyll. In a leaf hydrated from −3.4 MPa for 120 s, recovery in conduit shape and mesophyll turgor is uniform (C and D). The expected equilibrium water potentials, had the leaves come to internal equilibrium rather than been frozen, were −3 MPa (A and B) and −1.4 MPa (C and D).

Hydraulic Experiments

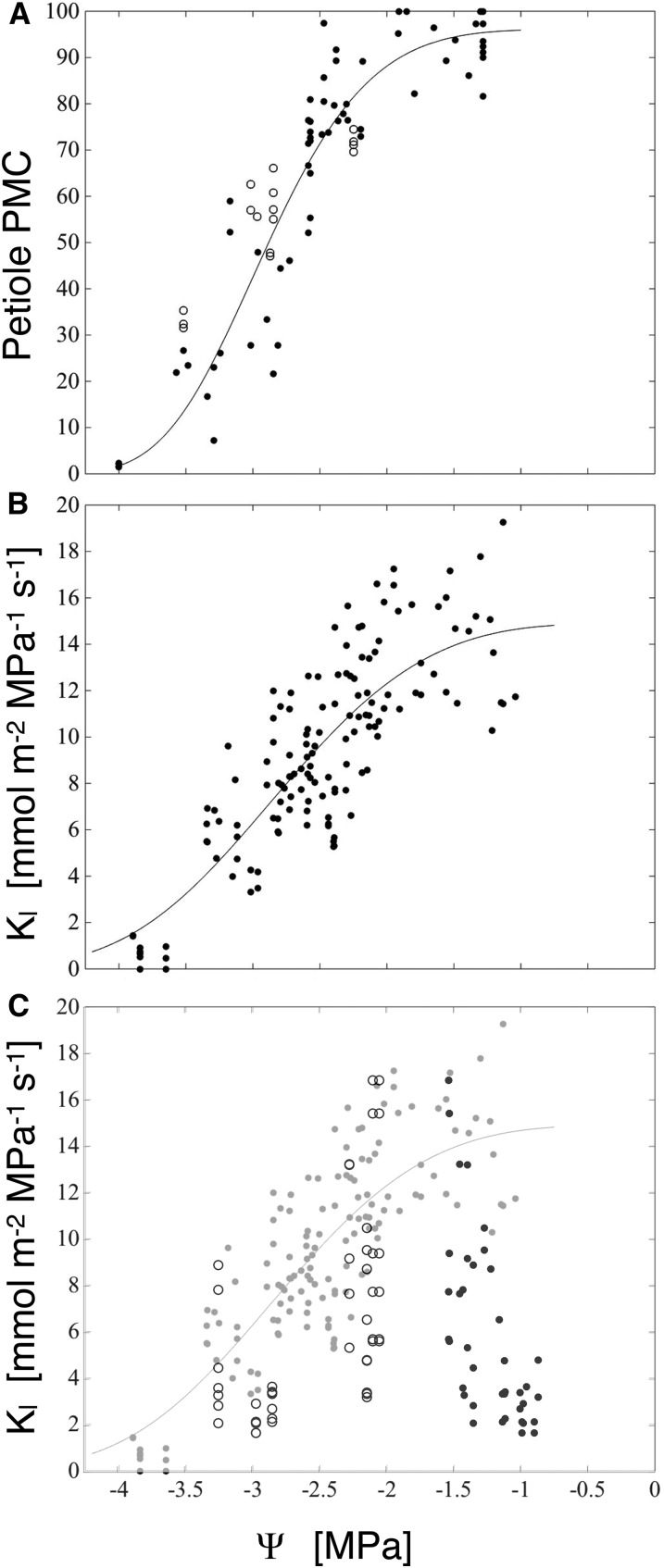
Petiole hydraulic conductance followed a sigmoid relationship with branch water potential, remaining above 80% of flushed values (henceforth percentage maximum conductance [PMC]) until xylem pressures fell below −2 MPa, then reaching minimum values between −3.5 and −4 MPa (Fig. 5A). To test for artifactual embolism induced by sampling petioles while their xylem was under tension (Wheeler et al., 2013; Torres-Ruiz et al., 2015), we relaxed branches to water potentials at which petiole conductance is expected to be at least 80% of flushed values (−1.7 to −0.1 MPa) before sampling; the resulting conductances were consistent with petioles sampled at their minimum water potentials, suggesting that cutting artifacts did not influence the shape of the vulnerability curve in an important way.

Figure 5.

A, Petiole conductance, as percentage maximum flushed values, versus branch water potential. Black circles, Petioles sampled at native water potentials; white circles, petioles sampled after relaxing branches to −1.7 to −0.1 MPa from their native minimum water potentials (plotted). B, K_l versus initial branch water potential; the line is a best-fit Weibull function. C, Leaf conductances from branches dried to a minimum water potential and rehydrated to between −1.6 and −0.9 MPa, then reequilibrated before measuring K_l. Rehydrated K_l is plotted versus branch minimum water potential (white circles), and the rehydrated branch water potential was measured at the time of the experiment (black circles); data in gray are K_l values replotted from B for comparison.

Leaf hydraulic conductance (K_l), as defined by rehydration kinetics (Brodribb and Holbrook, 2003; Rockwell et al., 2014b), declined with declining water potential in a manner broadly similar to both petiole conductance and indices of xylem conduit shape (Fig. 5B). Relaxing branches from water potentials at which leaf conductance was expected to be impaired (less than −2 MPa) to potentials at which no impairment had been seen (−1.6 < Ψ < −0.9 MPa) prior to measuring leaf conductance resulted in K_l values more consistent with the maximum stress experienced by the branch, rather than the water potential in the branch at the time of the experiment (Fig. 5C). The failure of K_l to recover following the relaxation of branch water potentials supports a dominant role for upstream embolism, rather than downstream conduit collapse, in limiting leaf conductance during rehydration experiments. Further support for embolism as the principal factor for the K_l declines in the rehydration experiments comes from the close congruence between the Ψ₅₀ (water potential at 50% loss of conductance) of the K_l and the petiole PMC (Table I). If collapse played a limiting role for K_l in these experiments, we would have expected a faster fall off of K_l with declining water potentials and a Ψ₅₀ close to that of the intrusive veins (type I HI; Table I), in the case of a strictly series-type xylem model, or both vein types combined, in the case that boundary veins also supply water to the mesophyll (grand HI; Table I).

Table I. Weibull fit parameters for hydraulic loss functions.

Quantity	Figure	s	Ψc	a	b	Ψ50
		−	MPa	−	−	MPa
Grand HI	2A	6.3	−2.65	0.16	0.60	−2.50
Type I HI	2B	7.38	−2.64	0.14	0.62	−2.51
Type B HI	2C	4.63	−2.95	0.15	0.59	−2.73
Petiole PMC	5A	5.54	−3.1	0	96.1	−2.91
Kl	5B	3.71	−3.12	0	14.89	−2.83

In apparent contradiction to the idea of petiole embolism-limited K_l, absolute petiole conductances were too high (mean flushed conductance of 371 ± 110 [sd] mmol m⁻² MPa⁻¹ s⁻¹; n = 91) to constitute a limiting conductance until water potentials became more negative than −3.5 MPa (PMC of <5%; Fig. 5). Yet, petiole sample conductances in red oak are so high precisely because, over the length of the petioles, many vessels are open and such vessels extend into the first, second, and third order veins (as attested to by preliminary tests made by pushing air into the petiole at low pressure, cutting open veins of different orders under water, and watching for the emergence of air bubbles). Embolism that occurs in the petiole then must extend into the higher vein orders, which have a lower absolute conductance (Sack et al., 2004). Therefore, we can resolve the apparent contradiction by interpreting petiole PMC as an estimate of the degree of embolism in the proximal vein orders of the blade. We did not attempt to quantify this embolism directly by cryo-SEM, as artifactual freezing-induced embolism would be difficult to rule out (Cochard et al., 2000). By contrast, we know of no process by which freezing could induce an artifactual lack of embolism in the minor veins.

Observation of changes in the refractive index of leaf vasculature during desiccation suggests that embolism appears first in the petiole and midvein of leaves, appearing in higher orders progressively as the leaf dries (Brodribb et al., 2016). Such observations are most easily explained by a model of leaf vulnerability in which the accumulation of embolism occurs primarily due to propagation, rather than de novo air seeding or heterogenous nucleation occurring independently throughout the leaf in any vein order. The first evidence of embolism in boundary-type veins in our imaging data comes from samples dried to −3.4 MPa, at which time the PMC of the petiole is approximately 25% (75% loss). Under a propagation-dominant model of embolism formation, we would then expect the xylem of the intervening vein orders to range between 75% and 4% loss of conductivity due to cavitation (4% is the average background level of unstressed leaves), with a large degree of variation possible between various paths and areoles. Such a pattern could explain the submillimeter-scale spatial heterogeneity seen in recovery during rehydration from similar water potentials (Fig. 4).

That the collapse of xylem conduits in the minor veins of red oak did not appear to affect measurements of K_l requires comment, especially as the collapse of transfusion tracheids was closely associated with declines in K_l in the conifers Podocarpus greyi and Taxus baccata (Brodribb and Holbrook, 2005; Zhang et al., 2014). The speed with which oak leaves rehydrate, coupled with the lack of any significant hysteresis in conduits returning to an unbuckled shape, means that much of the hydraulic effect of conduit collapse would have been lost early during the longer rehydration times required to measure K_l on leaves initially below their turgor loss points (due to the increased capacitance). In contrast, transfusion tracheids in T. baccata regain their original shape much more slowly (more than 10 min, rehydrated from −3 MPa; Y.-J. Zhang and N.M. Holbrook, unpublished data) when branchlets are given free access to water. The longer time needed for T. baccata tracheids to rebound may reflect a greater degree of viscoelastic deformation but also could be due to the greater hydraulic resistance of T. baccata xylem and, thus, slower flow rates.

Cryo-SEM Imaging of Buckling and Collapse in Living Cells

Our imaging also allowed us to follow the progress of buckling and collapse in the surrounding mesophyll of water-stressed samples (Fig. 6), behaviors that, when scaled up, contribute to whole leaf pressure-volume (PV) curves. PV analyses undertaken in support of rehydration experiments produced estimates of the leaf turgor loss point (Supplemental Fig. S4; −2.17 ± 0.1 [sd] MPa; n = 6) wetter than the transition in the imaging data from no evidence of mesophyll cell deformation to widespread wrinkling, folding, and faceting that occurred near −2.6 to −2.7 MPa (Supplemental Fig. S5). The apparent discrepancy may derive from the degree of volume loss that mechanical models suggest occurs after the primary cell wall has ceased to resist deformation (i.e. buckling) but before a cell shows gross visual signs of volume shrinkage (Ding et al., 2014).

Figure 6.

Heterogeneity across leaf cell types in deformation due to dehydration. A, At water potentials above the buckling point, all tissues appear equally turgid. B, At water potentials below the buckling point, the spongy mesophyll cells appear crumpled, while the palisade mesophyll cells are faceted along their long axes. The cells with the least mechanical freedom from their neighbors (epidermal and vascular parenchyma) show the least deformation. In the epidermal cells at top, deformation is seen in the lateral walls (white arrows), consistent with larger changes in thickness relative to area. The inset shows a 2× digital magnification of a deformed region of the lateral wall.

Given the same wall material properties and thicknesses, larger cells have a lower bulk modulus and experience larger deformations than small ones (Tyree and Jarvis, 1982). However, comparisons of cross sections from samples showing widespread mesophyll deformation (less than −2.6 MPa; n = 7) versus no such deformation (greater than −2.1 MPa; n = 7) found no important difference between the two groups in the average relative thicknesses of different tissue zones (upper epidermis, 12%; palisade, 52%; spongy, 28%; and lower epidermis, 8%). Therefore, changes in thickness during dehydration were evenly distributed among tissue layers and did not support our expectation that large upper epidermal cells would contribute the most volume loss. In the upper epidermis, changes in thickness manifested as a folding of the upper portions of the lateral walls (Fig. 6B, inset), while folding was never observed in the epidermal walls parallel to the leaf surfaces. Our images did not support a model prediction (based on similar cell sizes) by Ding et al. (2014) that the relatively small diameter of the cylindrical palisade cells would prevent them from buckling, perhaps because their simulations assumed a cell wall thickness four times the approximately 250 nm observed here.

Modeling Results

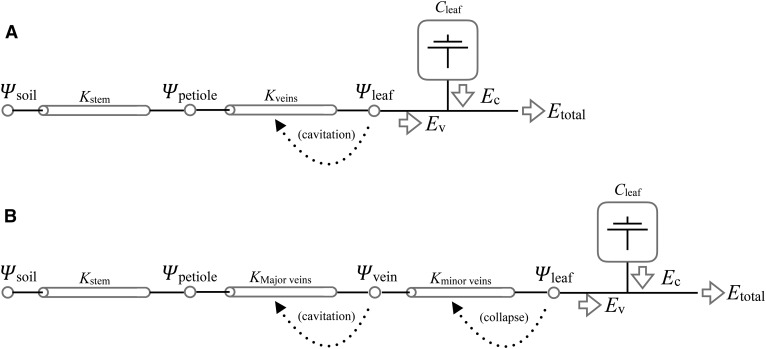
To investigate a hypothesized adaptive function of collapsing conduits, that of protecting upstream cavitation-prone xylem during a sustained perturbation to transpiration prior to an effective stomatal response, we compared two simple transient models of vascular flow in transpiring leaves similar in construction to that of Brodribb and McAdam (2011). We then challenged the models with an imposed doubling of transpiration (E) lasting 10 min. While the size and duration of the perturbation are arbitrarily chosen, the orders of magnitude are relevant to those of experiments on stomatal behavior (Mott and Parkhurst, 1991; Powles et al., 2006; Buckley et al., 2011). In the first model, the vasculature is represented as a conductor subject to loss of conductance based on the downstream (i.e. transpiring leaf) water potential (Fig. 7A). In the second, leaf vasculature is decomposed into two conductors in series, the first representative of the major veins and subject to cavitation and the second representative of the minor veins and subject to collapse (Fig. 7B). In this model, losses in conductance due to the cavitation of major veins and the collapse of minor veins are each a function of their immediate downstream water potential. Note that neither model includes any stomatal regulation (i.e. no feedback of leaf water status on transpiration). Rather, the imposed E is assumed to reflect the combined effects of an environmentally driven increase in evaporative demand and stomatal WWR, and we are interested in what happens to the leaf prior to the active rectification of stomatal aperture. While transpiration over the WWR and the following reduction in stomatal aperture to a new steady state generally follow a parabolic path, in order to avoid assuming a specific stomatal dynamic, we approximate the transient as a step change and investigate the relationship between transient duration and cavitation. That is, as we are interested primarily in effects that accumulate over time, the precise shape of the transient is of lesser importance.

Figure 7.

Schematics for two models of the loss of vascular function in leaves. A, In the cavitation-only model, the conductance of the leaf vasculature (K_veins) is determined by transpiring leaf water potential (Ψ_leaf). B, In the cavitation-and-collapse model, the conductance of the vasculature is split into two conductors in series, such that the major veins are subject to cavitation and the minor veins are subject to collapse, as driven by their vulnerability curves and the downstream water potentials. In both models, E_total, Ψ_soil, and K_stem are specified and invariant, and the flux from the living cells (C_leaf) is the capacitive discharge specified by a PV curve and Ψ_leaf.

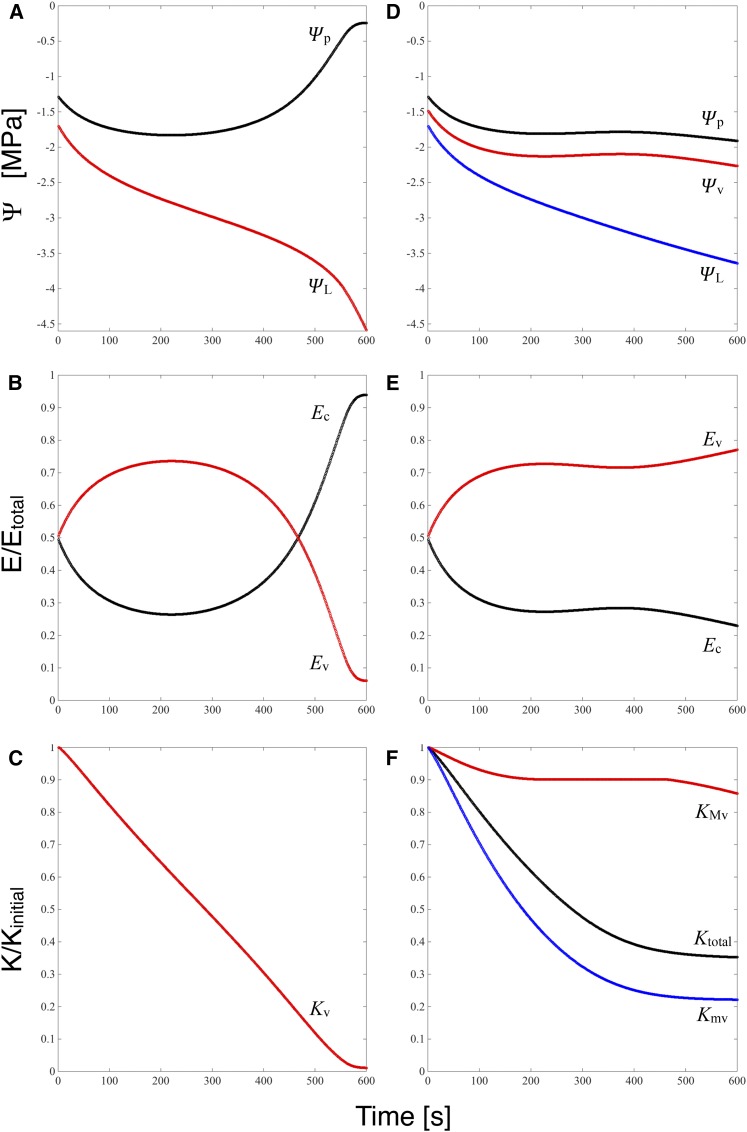
Prior to the imposed increase in transpiration, the flow of water through the leaf vasculature (E_v) is equal to transpiration: the leaf is at steady state. Following the perturbation, the increase in transpiration is supplied initially by discharge from storage as water is lost from living cells (E_c). The flux from storage then decays toward a new steady state (in which changes in water content are zero by definition; i.e. E_c = 0) as the decline in leaf water potential (Ψ_L) increases the flow rate through the vasculature. Attainment of a new steady state is delayed in both models by declines in vascular conductance that slow the increase in E_v and drive Ψ_L continuously lower. As leaf capacitance, which controls the time scale of the model responses, is the same in both models and as total vascular conductance (K_v in Fig. 8C and K_total in Fig. 8F) responds to water potential similarly in both models as well, over the first approximately 250 s the time course of Ψ_L (Fig. 8, A and D) as well as E_c and E_v (Fig. 8, B and C) in the two models are indistinguishable.

Figure 8.

Model results for an oak leaf subject to a doubling of transpiration and xylem subject to cavitation (A–C) or with cavitation restricted to the major veins and the minor veins subject to collapse (D–F). Quantities in red are related to cavitation, and those in blue are related to collapse. A and D, Water potentials at the stem-petiole junction (black), at the transition from major to minor veins (red), and at the vascular-mesophyll interface, equivalent in the model to the bulk-averaged Ψ_L (red in A and blue in D). B and E, Proportions of the transpiration flux E accounted for by flow through the veins (red) and capacitive discharge from living cells (black). C and F, Effect of cavitation on the conductance of the entire vasculature (C; red) or just the major veins (F; red); effect of collapse on the conductance of the minor veins (F; blue); and total conductance of the vascular network as affected by both cavitation and collapse (F; black).

In the cavitation-only model, this initial phase gives way after approximately 250 s to runaway cavitation; as K_v falls to its residual value (Fig. 8C), E_v falls and E_c increases to near 1 (Fig. 8B). In this context, runaway cavitation occurs if the transpiration E_total imposed in the perturbation exceeds the maximum of transpiration as a function of Ψ_L. In steady state,

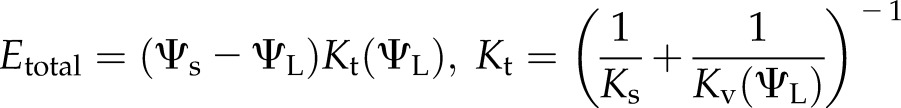(1)

where Ψ_s is soil water potential and K_s is the stem conductance. Taking the derivative with respect to Ψ_L and setting it equal to 0 predicts a maximum at the Ψ_L that satisfies,

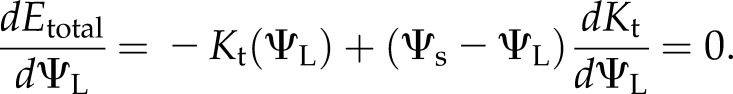(2)

Equation 2 defines a critical Ψ_L below which no steady state is possible. As water potential falls, K_t(Ψ_L) declines, while both the slope and water potential difference in the second term increase. The water potential at which the two terms in Equation 2 come into balance corresponds to the most negative water potential and degree of cavitation (here 40% loss of initial conductance), at which a stable steady state is possible. Evaluating E_total (Eq. 1) at the critical potential defines the maximum steady E_max attainable, which by inspection varies as a function of Ψ_s; in the absence of stomatal regulation, any perturbation in demand that would result in a steady state with an E higher than E_max leads to runaway cavitation. For the cavitation-only model in Figure 8, A to C, the critical value of E_total was 8.2 mmol m⁻² s⁻¹, or about approximately 1.4 times the initial steady-state E; the critical Ψ_L of −2.78 MPa was reached at around 220 s, about when the two models diverge.

In the model with collapse, cavitation in the major veins (Ψ_v) remained well controlled (Fig. 8D), as collapse of the more vulnerable and downstream minor vein conductance produced the decline in total xylem conductance (Fig. 8F) required to slow the rise of E_v and thus minimize any decline in Ψ_v. Because E_v is held in check, the discharge flux (E_c) is maintained (Fig. 8E) and Ψ_L falls (Fig. 8D). While the cavitation-and-collapse model had a higher critical E_total than the cavitation-only model (1.8 versus 1.4 times the initial flux), the imposed doubling of E_total was sufficient to ultimately induce runaway cavitation at longer times (data not shown).

Sensitivity of the Model

In considering the dependence of the above results on model structure and individual parameter values, a natural way to summarize the protective effect of collapse is the time over which hydraulic conductance of the major veins (K_Mv) remains nearly constant and the level at which it is held (e.g. for the model with collapse described above, we have approximately 250 s, over which major vein conductance holds steady at approximately 85% of its initial value; Fig. 8F). To assess the stress imposed by different scenarios on the living cells, we can consider the Ψ_L attained by the end of the protective period.

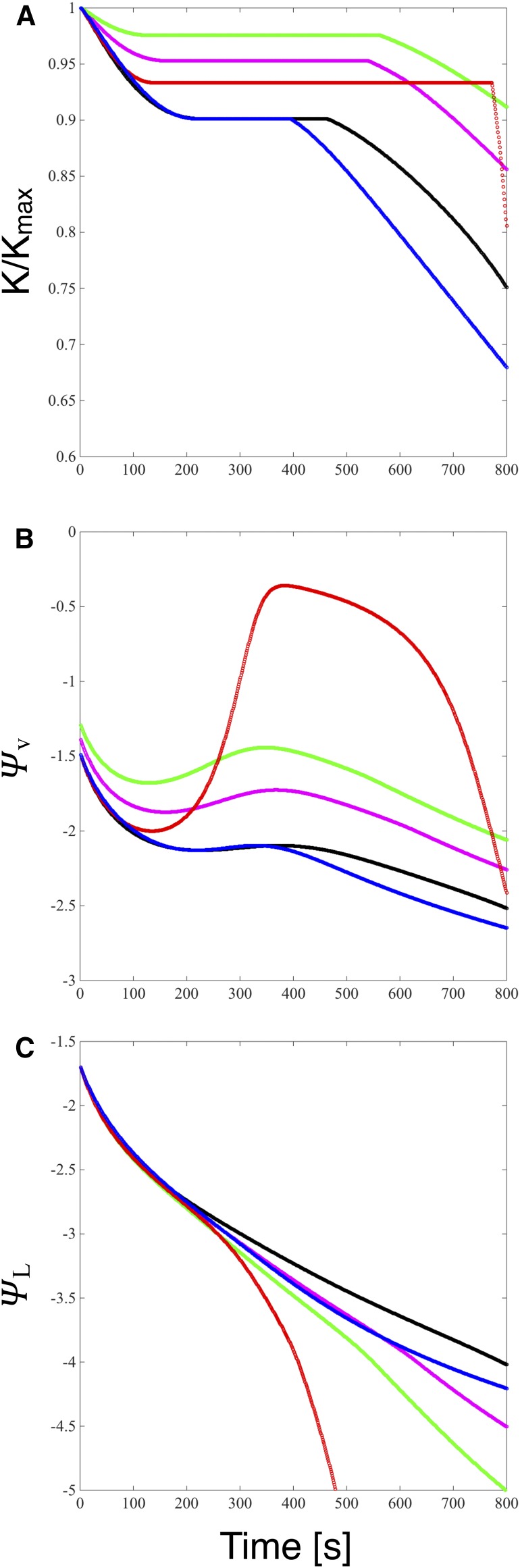
As there is some uncertainty in how best to transform the grand HI (Fig. 2A) to a vulnerability curve for the minor veins, we next ran the model with the minimal conductance of the minor veins lowered from 21% [a/(a + b) in Table I] to 1% of the initial value. As expected, lowering the residual conductance of the minor veins increased the effective protection of the upstream cavitation-prone xylem (approximately 88% PMC from 130 to 770 s; Fig. 9A) but also shortened the time to catastrophic Ψ_L (−27 MPa). Avoidance of such catastrophically low water potentials would constitute a major constraint on the strategy of increasing protection of the major veins from cavitation by reducing minor vein residual conductance; a circuit breaker isolating the major veins must leak enough to keep the mesophyll alive.

Figure 9.

Sensitivity of model results for the protective effect of collapse (A), vein water potential (B), and Ψ_L (C) to various parameters. Black, Baseline model with vascular resistance partitioned equally between major and minor veins. Blue, Using the lower 2015 capacitance curve shortens the duration of the plateau in conductance in B. Red, Lowering the residual conductance of the minor veins to 1% extends the plateau in the fall in conductance in A, greatly increasing the buffering of vein potential (Ψ_v) in B but at the cost of a catastrophic fall in Ψ_L (C). Increasing the proportion of total vascular resistance assigned to the minor veins from the 50% baseline to 75% (magenta) and 99% (green) shows a pattern of diminishing returns with respect to protective benefits (A) and Ψ_L costs (C).

We next assessed the partitioning of total vascular resistance between major and minor veins, assumed to be equal in the model with collapse. Vein-order cutting experiments have suggested that the majority of resistance is imposed by the minor vein orders (Cochard et al., 2004b; Sack et al., 2004), so we explored the effect of assigning 75% of the resistance to the collapsible minor veins. Increasing the minor vein proportion of resistance enhanced the upward bounce in vein water potential, resulting in less cavitation and extending the protective period in both time and amplitude (Fig. 9, A and B), with only a small decrease in water potential (Fig. 9C). Therefore, concentrating vascular resistance in collapsible vein orders appears to be an effective strategy, although one that faces diminishing returns.

We then investigated the effect of leaf capacitance. Running the collapse model with a lower leaf capacitance (based on data from the same trees but different years) shortened the protective phase from 470 to 400 s (Fig. 9A); in general, higher leaf capacitance extended protection in time without a further drop in water potential.

Finally, we considered the effect of neglecting stem capacitance in the model by assuming the opposite limit of infinite stem capacity and, thus, a fixed petiole water potential (Ψ_p); in such a model, collapse was more effective at protecting the upstream xylem for the trivial reason that the potential drop through the stem was independent of flow rate (data not shown). Overall, the general phenomena of minor vein collapse providing a buffer against upstream cavitation proved robust across all model structures.

DISCUSSION

“...it went to pieces all at once, all at once, and nothing first, just as bubbles do when they burst.” –From “The One Hoss Shay,” by Oliver Wendell Holmes.

From an equilibrium perspective, it seems that red oak leaves are built with respect to hydraulic function like the proverbial “One Hoss Shay”: mesophyll turgor loss, petiole cavitation, and terminal vein collapse all accelerate rapidly after water potentials decline below −2 MPa. If one then takes the further reasonable step of assuming that building a more robust leaf (more cavitation-resistant xylem, stiffer-walled terminal tracheids, and mesophyll that can maintain turgor to more negative water potentials) involves nontrivial costs, it may be regarded as evolutionarily efficient that the failure modes of these diverse tissues all occur at similar levels of stress: none is overbuilt relative to the other. Yet, in the life of the plant, such negative equilibrium potentials might only be obtained when stomata are shut and the soil dry (i.e. drought conditions), conditions that, in vivo, are likely to lead to leaf senescence.

From the nonequilibrium perspective of a transpiring leaf, our modeling demonstrates a plausible functional role for terminal vein collapse in protecting upstream xylem from cavitation. In comparing our modeled time scales of protection with transient durations in experimental data, it is important to remember that, in the model, the time of effective protection evolves following a large step change in E and in the absence of any stomatal down-regulation; therefore, protection due to collapse would be more effective than a simple comparison of time scales might suggest.

Cavitation has been proposed to act as an amplifier of water potential influences on stomatal aperture, one that, with subsequent repair of embolism, could explain the observed hysteresis in the water potential-stomatal conductance relationship (Buckley and Mott, 2002). However, cavitation reversal, when it occurs at all, requires that xylem water potentials relax to at least a few bars below zero over a time scale of hours (Hochberg et al., 2016; Knipfer et al., 2016), conditions that may not be met diurnally. Reversible collapse would be as effective as cavitation in increasing the gain of an abscisic acid (ABA) signal mediated by mesophyll turgor (or cell volume) during a transient increase in E (Zabadal, 1974; Pierce and Raschke, 1980; McAdam and Brodribb, 2016), even as it protected upstream xylem. In this case, hysteresis in stomatal aperture would be driven by ABA rather than by hydraulic factors. From the perspective of enhancing the movement of ABA out of the mesophyll into the apoplast, maintaining a large residual conductance in the minor veins would allow more time for stomatal responses to regulate E (Fig. 9). Here, we have shown that, even in highly desiccated leaves (less than −3MPa), some small conduits persist in a noncollapsed state (Fig. 1D), broadly consistent with a level of residual conductance expected in our models to emerge from a balance of competing functions.

While we have documented that the xylem of the smallest vein orders of red oak leaves collapses without cavitating down to water potentials below −3.5 MPa, potentials at which the vessels of the petiole (which extend into the major vein orders) are almost entirely cavitated. The structural bases for this divergence of fates remain unknown. Indeed, the structural bases for differences in vulnerability to cavitation, both within and between species, remain poorly understood (Gleason et al., 2016). However, there are developmental differences between the highest and lowest vein orders that may be pertinent. In an angiosperm leaf, the final highest vein orders develop late enough in leaf maturation that leaf expansion is nearly or entirely complete. As a result, the highest vein orders do not contain protoxylem (Russin and Evert, 1984), conduits with annular to helical thickenings that mature prior to the cessation of leaf expansion and are ultimately destroyed by axial stresses (Esau, 1960). Consistent with this theory, we observed only functional primary xylem with helical to scalariform secondary thickenings in the smallest boundary and intrusive veins of red oak. The destruction of protoxylem has been hypothesized to provide sites where metaxylem pits (once connected to protoxylem) now contact gas-filled spaces (Lens et al., 2013). That high vein orders lack such exposure may explain their apparent resilience to cavitation versus lower orders and why embolism spreads in leaves by propagation from low vein orders to high (Brodribb et al., 2016).

A limit to which minor veins can resist buckling may be imposed by the necessity of maintaining sufficient radial permeability to distribute water efficiently within an areole, thereby limiting the extent of helical-to-scalariform secondary thickening that supports but also occludes the primary wall of the conduits. While the distributions of perimeters for both intrusive veins and veins with bundle sheath extensions were broadly similar (Supplemental Fig. S1), the intrusive veins had more instances of large perimeters in the range of 30 to 60 μm. That wider tracheids should occur in the smaller vein order runs counter to the expected trend of smaller and fewer conduits toward the periphery of the network (Zwieniecki et al., 2006); a functional interpretation is that the larger size serves to increase the surface area of exposed primary wall over which radial outflow can occur. That the hoop stress induced by a particular level of xylem tension in a conduit wall increases with increasing radius sets up a tradeoff between the efficiency of the radial distribution of water and resistance to collapse.

The Role of Neighbors in Resisting Collapse

Our imaging shows that the collapse of xylem conduit walls follows a different phenomenology than expected based on the mechanical modeling of individual cells. In the classical analysis of a PV curve, the assumption is that cell walls cannot support a pressure difference where P_out > P_in and so fold inward (buckle) without resistance once the internal cell pressure drops to atmospheric: hence, turgor loss or zero internal-external pressure difference. Subsequent reductions in water potential are balanced only by the increase in the osmotic concentration that results from volume loss, as the pressure difference between inside and outside the cell (i.e. turgor) remains at zero. However, this mode of buckling can occur at other internal-external pressure differences besides zero. Oertli et al. (1990) have shown that a variety of living plant cells can support true negative internal pressures, or negative turgor. In mechanical models of individual cells, when the buckling point is reached the walls fold inward without further resistance, even as the internal-external pressure difference remains fixed: turgor does not rise to zero (Ding et al., 2014). As long as the turgor value is constant, its derivative with respect to further changes in water content is zero, and further reductions in water potential are balanced in the cell only by increasing the concentration of solutes. Buckling point may then be a more general term than turgor loss point for the transition to linearity in the 1/Ψ versus water content relationship.

In xylem conduits, the osmotic term is generally negligible, so the conduit lumens would be expected to collapse completely following buckling of the wall. Indeed, this is the interpretation for the behavior of collapsing accessory transfusion tracheids in P. greyi (Brodribb and Holbrook, 2005). However, for red oak, the degree of individual conduit deformation evolved over a range of water potentials spanning 2 MPa, with increasing tension in the xylem and deformation increasing together monotonically. The difference in behavior between the conduits of P. greyi and oak might be attributed to differences in lignification, but we would expect increased lignification to simply shift the buckling point to a lower water potential rather than change the behavior postbuckling. However, another difference between P. greyi and oak is that, in oak, the conduits of the minor veins are embedded in cylindrical veins surrounded by large bundle sheath cells that must deform to accommodate a reduction in xylem conduit volume. In P. greyi, the collapsing conduits are arrayed in a continuous plane parallel to the leaf surface, allowing all the conduits to flatten in a manner that reduces leaf thickness and yet does not require the tissues above or below the accessory transfusion tracheids to deform. The suggestion is then that, isolated from their vascular bundles, red oak conduits would show the binary collapse behavior seen in P. greyi. The fact that it takes large decreases in water potential to fully collapse red oak minor vein conduits after the buckling point indicates that the stresses induced by xylem tension are not borne solely by individual conduit walls but are transmitted by cell adhesion to their living neighbors in the vascular bundle. If the xylem conduits are not free to pull away from their neighbors, then the bundle sheath parenchyma must deform to accommodate a smaller volume of xylem. Because the concentration of solutes limits the postbuckling volume loss of bundle sheath parenchyma as the leaf dries further, cell adhesion within the vascular bundle could explain why xylem conduit collapse postbuckling is a gradual process with respect to xylem tension.

That cell adhesion can reduce the mechanical freedom of individual cells also could explain the asymmetric deformation in upper epidermal cells reported here. Previously (Rockwell, 2010), we observed that, over the range of a PV curve (−0.1 to −4 MPa), red oak leaves change in area by less than 2% while reducing thickness by more than 10%, while the internal air space increases from 13% to 26% of the gross volume. That shrinkage in area is relatively constrained compared with thickness is consistent with the folding we observed in upper epidermal cell walls normal to the cell surface and its absence in walls tangential to the leaf surface. The increase in air fraction must come at the expense of mesophyll cells, and these are notably less well connected in planes tangential to the surface and so freer to deform independently of their neighbors. These observations underscore that tissue structure, and not just individual cell properties such as wall thickness and diameter, must be considered in mapping whole-leaf PV curves onto cellular models of deformation.

CONCLUSION

Cryo-SEM imaging has revealed that cell-level mechanical behavior in both the xylem and living tissue of red oak leaves is richer and more diverse than expected by classical water relations theory. That the stability of water under tension is maintained even as the conduits undergo large deformations seems remarkable. The gradual collapse of xylem conduits in the water potential domain also is surprising and points to the importance of mechanical linkages between cells and, thus, details of leaf structure. The behavior of these mechanical linkages appears to be elastic given the rapid recovery in the time domain. Our model demonstrates that the vulnerability of a xylem conduit to collapse may plausibly be tuned by natural selection to provide protection for cavitation-susceptible major veins during transient excursions in E. Angiosperm leaves are expected to be particularly prone to such excursions, due to a reliance on subsidiary cell shrinkage to amplify guard cell opening that then leads to large WWR when evaporative demand increases. Yet, safety margins between stomatal closure and the cavitation of leaf xylem for angiosperms also have been shown to be small, or even negative, from an equilibrium perspective, a result that has motivated the hypothesis of diurnal embolism repair in leaves (Johnson et al., 2009). The finding of minor vein collapse in an angiosperm opens a new window into the question of how angiosperm leaves can operate a regulatory system that allows high gas-phase conductances at the cost of large wrong-way excursions, without resorting to large safety margins and their associated high opportunity costs.

MATERIALS AND METHODS

Plant Materials

This study was carried out from July to early October 2015. Experiments were performed on five mature irrigated red oak (Quercus rubra) trees growing on the campus of Harvard Divinity School in Cambridge, Massachusetts. Sun-exposed branches were collected with a pole pruner for measurements.

Ψ_L

Leaf water potential Ψ_L was measured using a Scholander-type pressure chamber (Soil Moisture Equipment) fitted with a digital gauge with 1-p.s.i. (6.9 kPa) resolution (DPG500; Omega Engineering).

Cryo-SEM

Cryo-SEM was used to study the dehydration-induced xylem cavitation and structural changes in leaf tissues. Branches 1.5- to 2-m-long bench dried to different water potentials were placed in black plastic bags for at least 2 h for water potential equilibration. Additionally, some bench-dried branches were rehydrated for varying times to examine the dynamics in recovery of potential leaf structural changes. Leaves were frozen with a precooled (with liquid nitrogen) copper clamp while still attached to the branch and stored in liquid nitrogen. An adjacent leaf was excised simultaneously from the branch for water potential measurements. Frozen samples stored in liquid nitrogen were transported to the Center for Nanoscale Systems at Harvard University for cryo-SEM studies. An approximately 5- × 5-mm leaf section was fixed in a custom sample holder while remaining submerged in liquid nitrogen. A cryo-transfer Shuttle VCT 100 (Bal Tec) was used to transfer the sample to a precooled chamber under vacuum for fracturing and coating. The sample was fractured using a knife cooled to −150°C to expose the leaf minor veins in cross section, etched for 5 to 10 min depending on water content at −100°C, and sputter coated with platinum at −130°C with a MED020 Coating System (Bal Tec). The samples were then imaged at an accelerating voltage of either 2 or 3.5 kV in an NVision 40 Dual-Beam focused ion beam and scanning electron microscope (Zeiss) with a cryogenic stage maintained at −150°C.

Hydraulic Conductance, Vulnerability, and PV Curves

We measured K_l following the leaf rehydration technique (Brodribb and Holbrook, 2003), with leaves bagged after rehydration for at least 15 min before water potential measurement to ensure that internal equilibrium had been reached (Rockwell et al., 2011). Branches approximately 1.5 to 2 m long were harvested before dawn and allowed to dry in the laboratory to the target water potential, then bagged for 2 h to ensure internal equilibrium. K_l was calculated from a lumped capacity model for leaf hydration appropriate for when xylem resistances become large relative to the extraxylery tissue (Brodribb and Holbrook, 2003; Rockwell et al., 2014b):

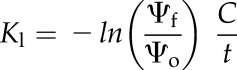(3)

where C is the leaf capacitance and t is the rehydration time in seconds. Leaf C (mmol m⁻² MPa⁻¹) was measured as the average slope of the PV relationship (Tyree and Hammel, 1972) between Ψ_o and Ψ_f, based on measurements of six leaves in July 2015. To examine whether the decline in K_l was reversible when water potentials were relaxed, some branches were rehydrated to a water potential between −1.5 and −1 MPa and reequilibrated, then K_l was remeasured as above.

Petiole hydraulic conductivity was measured with a Sperry-type apparatus (Sperry et al., 1988). The downstream ends of the petioles were connected to tubing and the flow rates were monitored using a balance (CPA225D; Sartorius). Flow was generated by a gravity-induced pressure head of 0.5 to 1 kPa, and 20 mmol of filtered (0.2 μm) KCl solution was used as the perfusion fluid. To establish the maximum conductance of a measured sample, petioles were flushed for 5 min with a pressure head of 0.15 MPa, after which the flow direction was reversed and the sample was flushed for another 5 min; preliminary tests showed that further flushing resulted in negligible gains or small losses in conductance. To check for artifacts resulting from cutting petioles under tension (Wheeler et al., 2013), a subset of branches were relaxed from their native water potentials to within a range from −1.7 to −0.1 MPa, and new petioles were sampled for conductance measurements.

The relationship between water potential and conductance was then fit to a Weibull type function with the form,

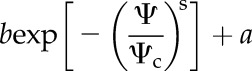(4)

where b represents the average maximum conductance or PMC of petioles, Ψ_c is the characteristic water potential, the exponent s determines the shape of the curve, and a represents a residual conductance independent of water potential. For K_l and PMC, the parameter a was assumed to be zero.

Image Analyses

Cryo-SEM images were analyzed using ImageJ (National Institutes of Health). HI, which describes a hydraulically weighted measure of roundness based on the measured area and perimeter of each conduit, was used to quantify the degree of collapse of xylem conduits. HI for an individual conduit was calculated by dividing the area of a conduit by the area of a circle with the equivalent perimeter of that conduit and then squaring this ratio to make it proportional to the fourth power of the radii, as in the Hagen-Poiseuille equation for pipe flow. HI, therefore, has a theoretical maximum of 1 that decays toward 0. To calculate HI for all the conduits imaged from a particular cryo-SEM sample, or for all of the conduits of a particular type (intrusive veins or veins with bundle sheath extensions) within a sample, we constructed the ratio of the sum of squared measured areas to the sum of squared equivalent circle areas. We then fit a Weibull-type function (Eq. 4) to the relationship between HI and sample Ψ_L. We also quantified the proportion of conduits of each type whose perimeters contained a region of negative (concave) curvature.

Models of Leaf Vascular Responses to a Perturbation in E

Model Structures

To investigate the implications of minor vein conduit collapse, we compared the responses of two models of vasculature to a perturbation in transpiration in the absence of any stomatal regulation (Fig. 7). In the first model, the entire leaf vascular system was represented as a single conductor subject to cavitation; such a model is consistent with previous efforts to relate the cavitation of leaf vasculature to Ψ_L (Johnson et al., 2009; Brodribb and McAdam, 2011). In the second model, the vascular system is split into an upstream major vein conductor subject to cavitation and a downstream minor vein conductor subject to collapse.

In both models, the imposed transpiration rate (E_t) is met by the withdrawal of water from living cells downstream of the xylem (E_c) and water transported through the leaf xylem (E_v). The discharge of water from the leaf tissue downstream of the xylem is specified by the leaf’s capacitance and the change in Ψ_L between time steps. As Ψ_L is thought to represent the bulk average water potential of the leaf tissue (Boyer, 1995), this step is equivalent to assuming a uniform capacitance through the tissue and integrating the discharge over all cells. In both models, Ψ_L also is taken as the water potential at the vasculature-mesophyll interface. This step is justified for oak leaves by previous modeling work showing that, for an hypostomatous leaf in which a majority of the water content resides above the plane of the vasculature, Ψ_L sits very close to the vascular-mesophyll interface potential (Rockwell et al., 2014a). Although mesophyll conductances to vapor and liquid water fluxes are not represented in the model, this does not imply that we assume them to be negligible. Rather, these conductances would appear only if we included a node for epidermal and/or stomatal water potential in the model.

Finally, for both cases, we model the water potential at the petiole Ψ_p as the potential drop resulting from the flux through a constant stem conductance: we neglect both cavitation in the stem and stem capacitance. The former assumption appears reasonable given that the data modeled are for irrigated trees and the downstream stem potentials (covered leaf), both modeled and measured, do not fall below −2 MPa. Neglecting stem capacitance lacks rigorous justification; we simply lacked the data to parameterize that variable. Therefore, we also ran both models with Ψ_p fixed, corresponding to the other extreme of infinite stem capacitance. The effects of these different constructions on model behavior are reported in the results.

Parameterization and Calculation

Both models were initialized with previously published steady-state and PV curve data (Rockwell et al., 2011, 2014a) for Ψ_p = −1.29 MPa, Ψ_L = −1.69 MPa, C_leaf as a continuous function of Ψ_L, and the transpiration rate E_t = 5.6 mmol m⁻² s⁻¹. To paramaterize C_leaf, we faced a choice of using the capacitance function generated by our 2015 PV data (Supplemental Fig. S4) versus the capacitance function (on the same trees) published previously with the flux data on which the initial steady state was based (Rockwell et al., 2011, 2014a). The two curves were similar, so we chose the older data for the default C_leaf curve (turgor loss point of −2.58 MPa for the older data versus −2.17 for the 2015 curve, and average slopes above and below that point of 0.393 ± 0.027 and 1.286 ± 0.172 mol m⁻² MPa⁻¹ versus 0.37 ± 0.102 and 0.971 ± 0.311, respectively, for 2015). Note that the turgor loss points and slopes are provided for descriptive purposes; for the model, we used the derivative of a smooth polynomial fit to the PV data, which provides capacitance as a continuous function of water potential. Stem conductance was calculated as E_t ÷ (Ψ_s − Ψ_p), where Ψ_s was assumed to be −0.1 MPa, a typical predawn value for these irrigated trees. The initial value of the vascular conductance (K_v) for the cavitation-only model (K_veins in Fig. 7A) was calculated from the initial steady-state data as E_t ÷ (Ψ_p − Ψ_L), where the denominator represents the difference between covered and Ψ_L. For the cavitation-and-collapse model, initial values for both the conductance of the minor veins (K_mv) and the major veins (K_Mv) were set by dividing the single vascular conductor of the first model into two equal conductors in series. To incorporate the effect of cavitation, K_veins (cavitation-only model) and K_Mv (cavitation-and-collapse model) were turned into functions of water potential by fitting them to K_max × PMC[Ψ]/100, where PMC is the functional form of Equation 4 with the coefficients from the fit to petiole PMC in Table I, with one modification to avoid dividing-by-zero errors: we specified a 1% residual conductance by reducing b from 96.1 to 95.1 and increasing a from 0 to 1. K_max was then fitted to produce the conductance of the initial steady state at the relevant initial downstream water potential (Fig. 8). To find K_mv[Ψ], we again adopted the form of Equation 4 with the parameters for the grand HI from Table I, normalized by a + b, multiplied by a K_max again chosen to produce the specified initial conductance at the initial Ψ_L. Leaf capacitance as a function of water potential, C_leaf[Ψ], was found by taking the derivative of a polynomial fit to the PV data of Rockwell et al. (2011). The resulting set of equations is available in Supplemental Text S1 and S2 coded for Mathematica (Wolfram Research).

For the sake of computational efficiency, we used the approach of Brodribb and McAdam (2011), which lags some calculations one time step to avoid the necessity of solving simultaneous equations in each iteration of the model; for time steps small relative to the time to steady state, the resulting errors are trivial. Here, we lag calculation of the xylem flux one time step behind discharge from the cells. For example, in the collapse-and-cavitation case in a given time step i, square brackets denote a list of the values a function takes over the time series and parentheses indicate the value of a function at a particular value of its driving variable.

1. We first calculate xylem conductances and leaf capacitance at the water potentials of the previous time step (for the first step, those are the potentials of the initial state):

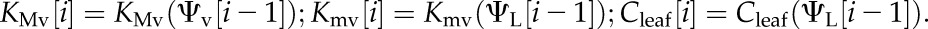(5)

2. We then calculate the flux through the xylem E_v as

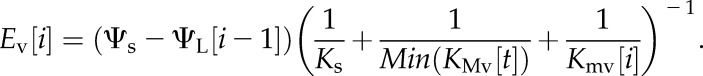(6)

Here, Min(K_Mv[t]) denotes the lowest conductance value realized for the major veins up to the current time step, which accounts for the hysteresis of conductance with water potential that occurs when xylem cavitates. For the sake of simplicity, we neglect gravity in calculating the soil-to-leaf water potential gradient, as soil water potential here is specified according to the hydrodynamic pressure drop to petiole water potential through a specified stem conductance, and so net a constant gravitational offset.

3. Next, we calculate the discharge flux from storage required to meet the imposed total transpiration flux

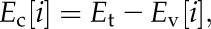(7)

and the change in Ψ_L required to produce the discharge flux,

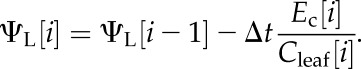(8)

4. At this stage, everything is known, and Ψ_p and Ψ_v can be calculated as

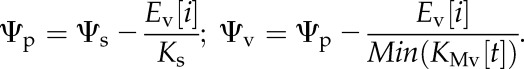(9)

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Normalized frequency distribution of conduit perimeters from intrusive and boundary veins.

• Supplemental Figure S2. Frequency distribution for conduit HI values for intrusive and boundary veins as a function of water stress.

• Supplemental Figure S3. Conduit perimeters versus HI values as a function of water stress.

• Supplemental Figure S4. PV curve for red oak leaves.

• Supplemental Figure S5. Proportion of intrusive veins showing buckling versus Ψ_L.

• Supplemental Text S1. Mathematica code for model with cavitation only.

• Supplemental Text S2. Mathematica code for model with cavitation and collapse.

Glossary

WWR

wrong-way response

cryo-SEM

cryo-scanning electron microscopy

PMC

percentage maximum conductance

PV

pressure-volume

ABA

abscisic acid

HI

hydraulic index