Magnetotail energy dissipation during an auroral substorm

Abstract

Violent releases of space plasma energy from the Earth’s magnetotail during substorms produce strong electric currents and bright aurora. But what modulates these currents and aurora and controls dissipation of the energy released in the ionosphere? Using data from the THEMIS fleet of satellites and ground-based imagers and magnetometers, we show that plasma energy dissipation is controlled by field-aligned currents (FACs) produced and modulated during magnetotail topology change and oscillatory braking of fast plasma jets at 10-14 Earth radii in the nightside magnetosphere. FACs appear in regions where plasma sheet pressure and flux tube volume gradients are non-collinear. Faster tailward expansion of magnetotail dipolarization and subsequent slower inner plasma sheet restretching during substorm expansion and recovery phases cause faster poleward then slower equatorward movement of the substorm aurora. Anharmonic radial plasma oscillations build up displaced current filaments and are responsible for discrete longitudinal auroral arcs that move equatorward at a velocity of about 1km/s. This observed auroral activity appears sufficient to dissipate the released energy.

Introduction

Substorms ¹ are magnetospheric disturbances during which energy is released from the tail of the Earth’s magnetosphere and injected in the inner magnetosphere and ionosphere. The development of an auroral substorm ², the visible part of a magnetospheric substorm, has been investigated for the past half century. Multispacecraft observations have revealed that a substorm onset sequence is initiated by magnetotail reconnection ³. Newly reconnected field lines relax their magnetic tension, generating series of earthward flow bursts (bursty bulk flows or BBFs) ^{4, 5} that encompass magnetic flux fronts. Because the velocity of newly reconnected magnetic flux in these fronts is substantially lower than that of a flow burst’s core, the fronts partly dissipate BBFs’ kinetic energy through thermalization and diversion of plasma flows ^{6, 7}. Earthward flow bursts are associated with small auroral expansions ⁸.

Low entropy BBFs overcome the pressure balance inconsistency ^{9, 10}, enabling magnetic flux transport to the inner magnetosphere. When BBFs deposit flux from the tail to the inner magnetosphere, the magnetotail dipolarizes ^{11, 12}, first around ten Earth radii (R_E), then farther downtail ^{13, 14}. Encounter with and oscillations of the dominant dipolar magnetic field finally brake flow bursts ^{15, 16}, and magnetic flux fronts.

Rapid modification of pressure and entropy distributions in the inner magnetosphere by a slowing flow burst has been suggested to generate an enduring substorm current wedge ¹⁷. In addition, azimuthal displacement or bending of field lines in the tail may provide dynamic balancing of the plasma sheet through closure of transient currents in the ionosphere as north-south (meridional) Pedersen currents across the auroral arc ^{18, 19}.

Using simultaneous observations in the near-Earth plasma sheet by five Time History of Events and Macroscale Interactions during Substorms (THEMIS) probes ²⁰, conjugate ground all-sky camera observations from Canada, and magnetometer arrays over North America on 23 March 2009 between 6:00 and 6:40 UT, we investigate the source of dissipation of magnetotail energy released when flow bursts stop. Magnetotail observations were provided by the probes’ fluxgate magnetometers (FGM) ²¹ and their electrostatic analyzer (ESA) particle detectors ²². Ground-based observations of auroral emissions and the ionospheric magnetic field were provided by the All-Sky Imagers (ASI at Snap Lake, Rankin Inlet, and Sanikiluaq) and a dense network of ground magnetometer (MAG) arrays over Greenland and North America ^23–25. A fortuitous THEMIS probe configuration in space and with their magnetic footpoints over the aforementioned network of MAGs and ASIs under clear skies, allowed us to unambiguously ascertain the physical connection between ground and space phenomena for an isolated substorm.

23 March 2009 Auroral Substorm

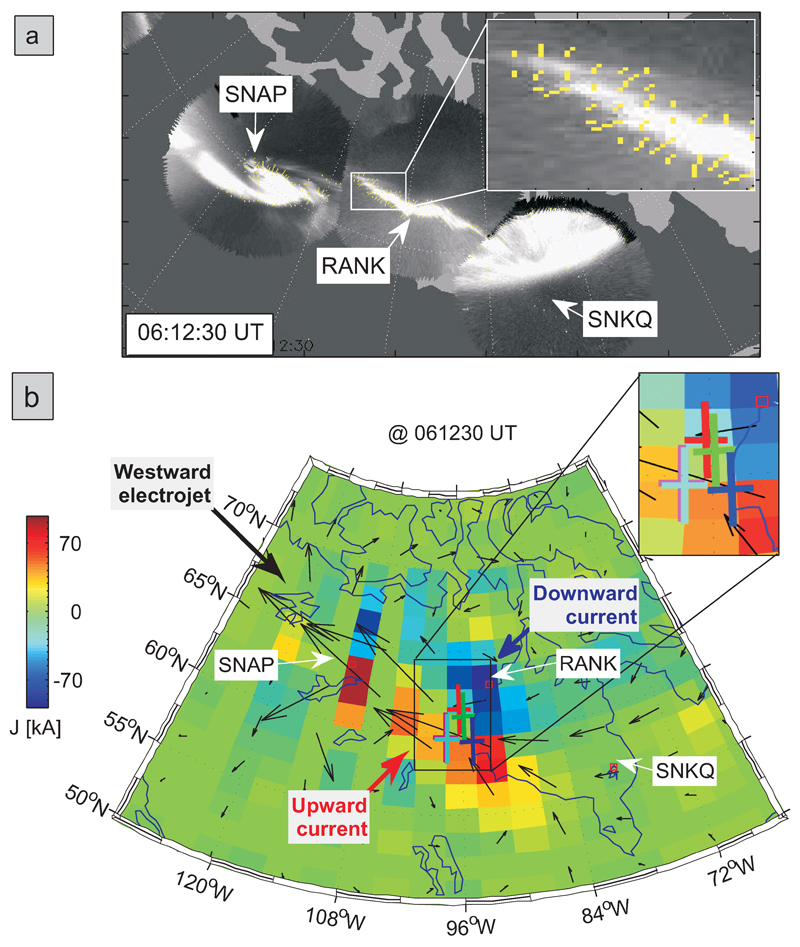
On 23 March 2009 at about 6:04 UT, THEMIS ASIs at Snap Lake (SNAP), Rankin Inlet (RANK), and Sanikiluaq (SNKQ) in Canada started to observe an auroral substorm. Figure a shows a snapshot (at 6:12:30 UT) from the three ASIs. The ASI at SNAP observed a westward traveling surge (a bright bold spot), whereas ASI at RANK observed most of an auroral bulge. The ASI at SNKQ observed the eastward end of an auroral bulge. Note that ASIs at SNAP and SNKQ were contaminated with a non-auroral light (stable white spots at the western edge of ASIs at SNAP and at the northern edge of ASI at SNKQ). A movie (in the auxiliary material) containing all ASI snapshots on 23 March 2009 between 6:00 and 6:40 UT at 3 second cadence shows the dynamics of the two auroral structures throughout the substorm. Between 6:04 and 6:17 UT the auroral bulge expanded northward by more than 7 degrees latitude. After 6:17 UT it started to fade away.

The length and orientation of tiny yellow lines in the snapshot (see zoom-in insert in white rectangle in Figure a) indicate the magnitude and direction of the auroral substructures’ local velocities (the lines’ origin is always at the edge of an auroral substructure). These velocities were calculated using a computer vision algorithm that solves the optical flow constraint equation. Optical flow is the distribution of apparent velocities of objects in an image (auroral substructures within the ASI snapshots). By estimating optical flow between video frames, one can measure the velocities of objects in the video. We solved the optical flow constraint equation using the Lucas-Kanade method, which divides the original image into smaller sections and assumes a constant velocity in each ²⁶.

Ionospheric Currents

We used magnetometer arrays over Greenland and North America ^23–25 and the 2D Spherical Elementary Current Systems (SECSs) method ^{25, 27} to investigate ionospheric currents on the ground. In this method, the divergence-free elementary current system is expanded at each pole of the grid shown in Figure 2 of ²⁵, allowing derivation of horizontal equivalent ionospheric currents (EICs). Using EICs, we calculated vertical components of the curl of EICs integrated over each grid point area. We refer to the vertical components as SECS scaling factors because the amplitude of each elementary system is scaled (measured in amperes). If the ionospheric conductance gradient is parallel to the electric field direction, the SECS scaling factors are proportional to field-aligned currents (FACs) ²⁷, and the factor of proportionality between FACs and the SECS scaling factors is the Hall-to-Pedersen conductance ratio.

Figure b shows a snapshot of EICs (arrows) and SECS scaling factors (color: upward, reddish; downward, bluish) at 6:12:30 UT (see movie containing all snapshots for 23 March 2009 between 6:00 and 6:40 UT at 1 second cadence in auxiliary material).

The ionospheric current system consists of a pair of vertical (FAC) currents with opposite polarity (reddish and bluish spots in the SECS scaling factors) and a westward electrojet (larger arrows in EICs between the reddish and bluish spots). Between 6:04 and 6:17 UT the ionospheric current area appeared to drastically expand in both the azimuthal and north-south directions. The current maxima moved northward from about 59 degrees latitude to about 63 degrees latitude (close to RANK) between 6:04 and 6:17 UT. By 6:40 UT the ionospheric currents had almost died out. The expansion, northward motion, and dying out of the ionospheric currents thus coincided with the auroral bulge behavior.

Linking an Auroral Substorm with Plasma Sheet Dynamics

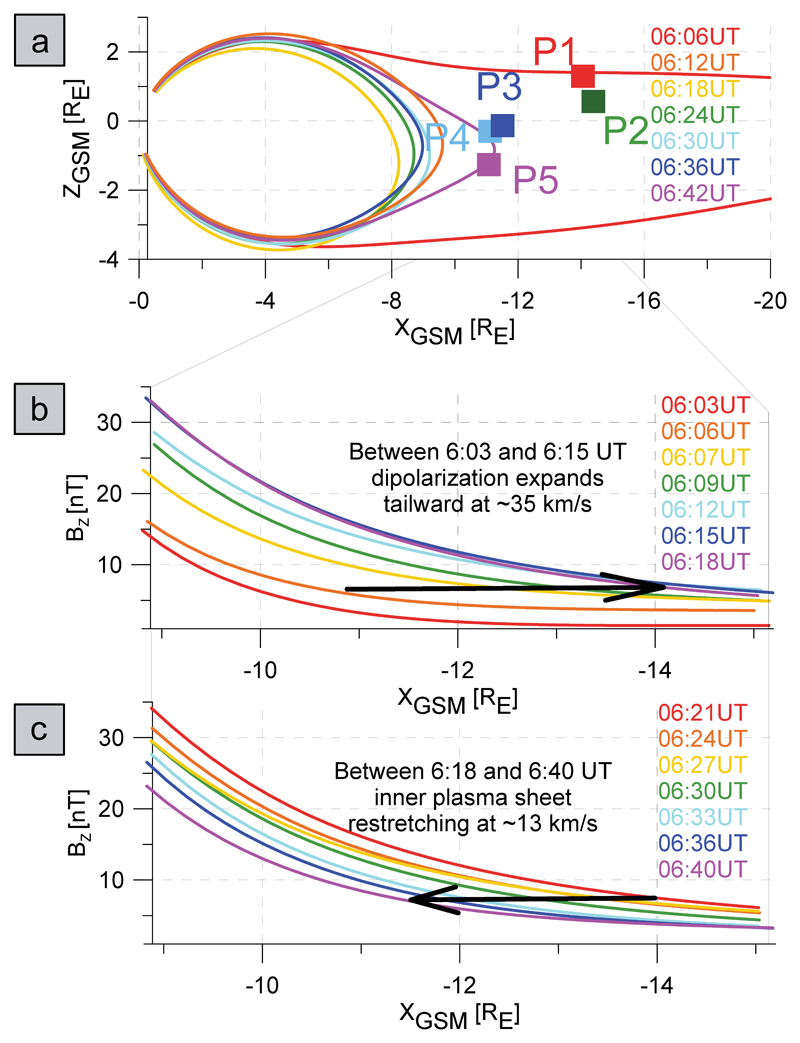
The appearance and fading away of the auroral bulge and ionospheric currents reflect the substorm expansion and recovery phases. Assuming that auroral and ionospheric current dynamics originate in the magnetosphere, observations in the plasma sheet may provide a clue about the substorm generation process. The expansion and recovery phases are not one-dimensional (radial) problems. In particular flow divergence in the out-of-plane direction may be responsible for an azimuthal flux transport ²⁸. During the time under discussion, five THEMIS probes (P1-P5) were orbiting inside the near-Earth plasma sheet between -11 and -14 Earth radii (R_E) downtail (Figure a), with their ionospheric footprints in the northern hemisphere near ASI at RANK (see zoom-in insert in black rectangle in Figure b). Such spacecraft location allows us to link plasma sheet and ground ASI and MAG observations near the central part of the auroral bulge.

According to the AM03 model ²⁹, magnetic field line evolution shows that the magnetotail depolarized rapidly between 6:04 and 6:17 UT. After 6:17 UT, magnetic field lines started to stretch tailward. The dipolarization and stretching cover a wide range of x (GSM). As indicated by the black arrow in Figure b, the plasma sheet B_Z magnetic field grew between 6:03 and 6:18 UT (during magnetotail dipolarization), such that the B_Z increase propagated tailward (from X = −11R_E to X = −14R_E) at a velocity of 35km/s. In contrast, after 6:18 UT (during magnetotail restretching), B_Z decreased earthward at a velocity of 13km/s (from X = −14R_E to X = −11.5R_E, black arrow in Figure c).

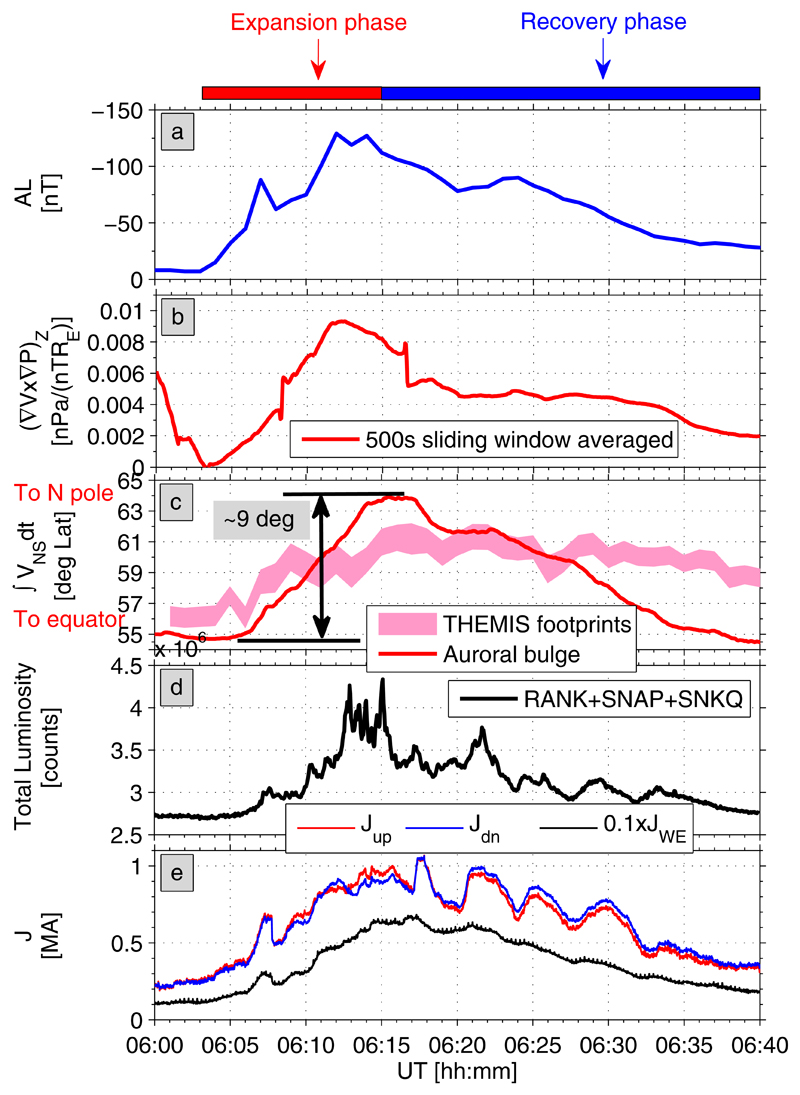
The auroral electrojet (AL) index (Figure a) reveals substorm expansion (between about 6:03 UT and 6:15 UT) and recovery (after 6:15 UT) phases. Magnetospheric perpendicular currents may divert to parallel because of zero divergence of total (perpendicular plus parallel) current density. For example, when the ions cannot carry all needed perpendicular current in a stronger total field, the divergent (to parallel) diamagnetic perpendicular current is proportional to ∇V × ∇P ³⁰, where P is plasma sheet pressure and V is flux tube volume. The triangular configuration of THEMIS probes in the xy plane (see ionospheric footprints in the northern hemisphere near ASI at RANK, zoom-in insert in black rectangle in Figure b) allowed us to calculate the Z GSM component of ∇V × ∇P in the region between the probes, where V is calculated using formula (6) in ³¹. The main component contributing to ∇V × ∇P appeared to be $\frac{\partial V}{\partial x}\frac{\partial P}{\partial y}.\frac{\partial V}{\partial x}$ was estimated between THEMIS probes separated along x GSM and confirmed by the AM03 model.

Regions of enhanced (∇V × ∇P)_Z around the neutral sheet are believed to feed substorm field-aligned currents, as shown by MHD simulations in Figures 4 and 5 in ¹⁹. According to these simulations, field-aligned current is oppositely directed on two sides of the flow burst’s core. Kinetic particle-in-cell simulations ⁷ indicate that these currents may be asymmetric due to strong duskward ion flow at the magnetic flux front.

Indeed, Figure b shows that (∇V × ∇P)_Z grew rapidly during the substorm expansion phase and decreased slowly during the substorm recovery phase. This behavior agrees with development of substorm currents in the ionosphere, Figure e.

The time-integrated average meridional auroral velocity at SNAP, RANK, and SNKQ ∫ V_NSdt (red curve in Figure c) indicates that during the substorm expansion phase, auroral activity moved poleward by about 9 degrees (from about 55 to 64 deg latitude). During the substorm recovery phase, ∫ V_NSdt slowly returned. The ratio between the velocity of tailward expansion of plasma sheet dipolarization (≈ 35km/s, cf. Figure b) and the poleward propagation velocity of the auroral activity (≈ 1.8km/s) is close to the ratio between the velocity of inner plasma sheet restretching (≈ 13km/s, cf. Figure c) and the equatorward propagation velocity of the auroral activity (≈ 0.7km/s). Because of the earthward then tailward convection of magnetic field lines past the THEMIS probes (Figure a), the geographic latitude of the five THEMIS footprints predicted by the AM-03 model (pink area in Figure c) appeared to partly follow the auroral activity location. In effect, Figures c,d show that a poleward fast-moving bright aurora slows down and dims after the expansion phase, recedes to lower latitudes, then fades away during late substorm recovery phase.

The above observations indicate that non-collinear pressure and flux tube volume gradients in the magnetotail indeed feed the direct part of the ionospheric currents (DC). However, as seen from the ASI observations, auroral activity within the auroral bulge near the maximal ionospheric currents (near RANK) is quite complex (Figure d), and alternating ionospheric currents exist there (Figure e). The amplitudes of the alternating currents are significantly smaller than those of the DC currents; thus, they do not change the direction of the total current.

Aurora During Anharmonic Oscillatory Braking

As predicted by the AM03 model ²⁹, the footprints of THEMIS probes P1 and P2 at the auroral bulge location most of the time. That is, they were located between the red and blue spots of upward and downward ionospheric currents at the westward electrojet current (see movie containing all snapshots of ASI observations at Rankin Inlet on 23 March 2009 between 6:00 and 6:40 UT at 3 second cadence in auxiliary material).

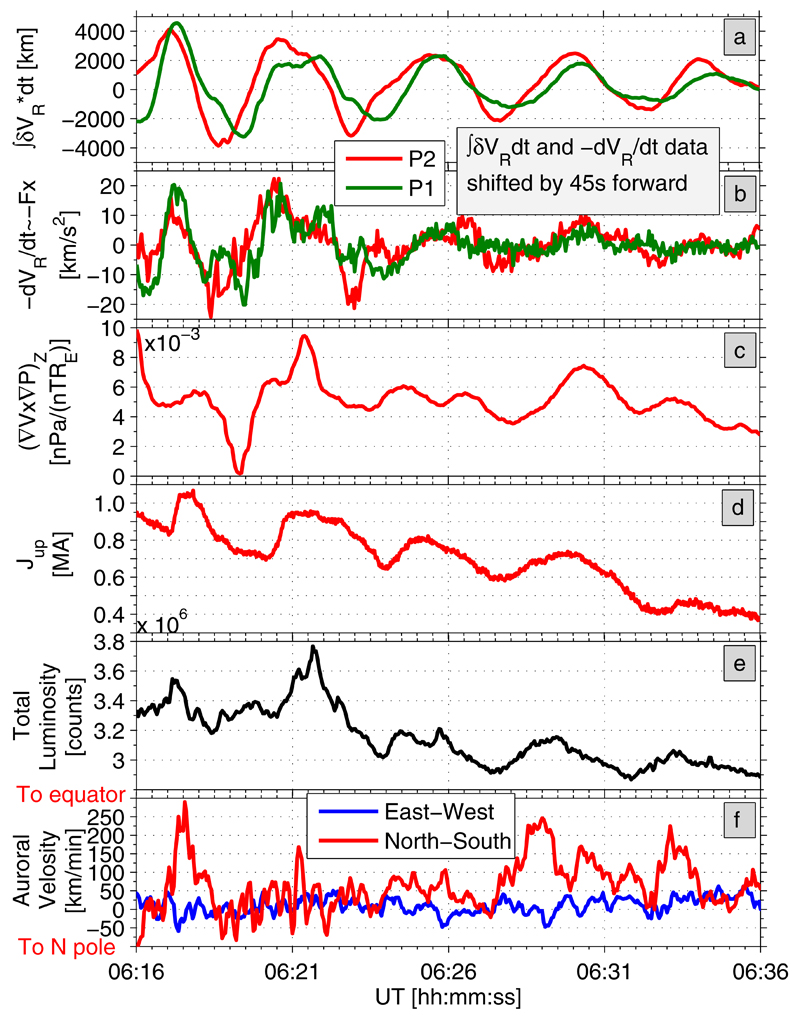
In Figure a we show ∫ δV_Rdt – time-integrated oscillations of the radial ion velocity V_R, where δ indicates band pass filtering at periods between 10 and 500 s, and positive V_R means earthward. The location of the oscillating magnetic flux tube with respect to its equilibrium position is indicated by ∫ δV_Rdt. When the oscillating flux tube was earthward of this position (i.e., when red and green curves in Figure a were above zero), the force acting on it (Figure b) was directed tailward (toward the equilibrium position). During such intervals (∇V × ∇P)_Z in Figure c exhibited peaks. Hence, the plasma sheet field-aligned current is modulated by the oscillating magnetic flux tube, getting stronger or weaker depending on the location of the oscillating magnetic flux tube with respect to its point of equilibrium. In contrast to the steady (DC) component of (∇V × ∇P)_Z from Figure b, the alternate (AC) component of (∇V × ∇P)_Z in Figure c may be partly balanced by inertial currents, agreeing with thin filament simulations. Nonetheless, ground J_up (Figure d) still reveals significant (up to 15% of an average magnitude) oscillations.

We correlated space ∫ δV_Rdt and ground J_up observations. We found that the ionospheric current dynamics lags behind THEMIS observations by about 45s (e.g., a plot of ∫ δV_Rdt against J_up (not shown) reveals a linear dependence, with the correlation coefficients exceeding 0.9). This time delay is about 15%; the observed oscillation period of ∫ δV_Rdt is about 5 minutes. This represents a phase lag of about 1 radian, which is consistent with Figure 25 of ¹⁵ for a reasonable level of an average Pedersen conductance in the ionosphere of 3 S.

The intervals of positive ∫ δV_Rdt correspond to about 10% – 15% increases in the ionospheric field-aligned currents (Figure d). Every peak in the field-aligned currents corresponds to enhanced auroral luminosity (Figure e) and velocity (Figure f) of the auroral arcs like the one shown in Figure at RANK (two more arc examples are given in auxiliary material for ground ASI and current observations at 6:17:30 UT and at 6:21:00 UT). The arcs were longitudinally oriented and moved equatorward at a velocity up to 200km/min (with an average value of the order of 50km/min, Figure f). The velocity of the auroral activity (Figure f) peaked when the magnetic flux tube moved earthward from its equilibrium position. Hence, magnetic flux tube oscillations during fast flow braking in the near-Earth plasma sheet modulated the ionospheric current and auroral dynamics during the substorm under study.

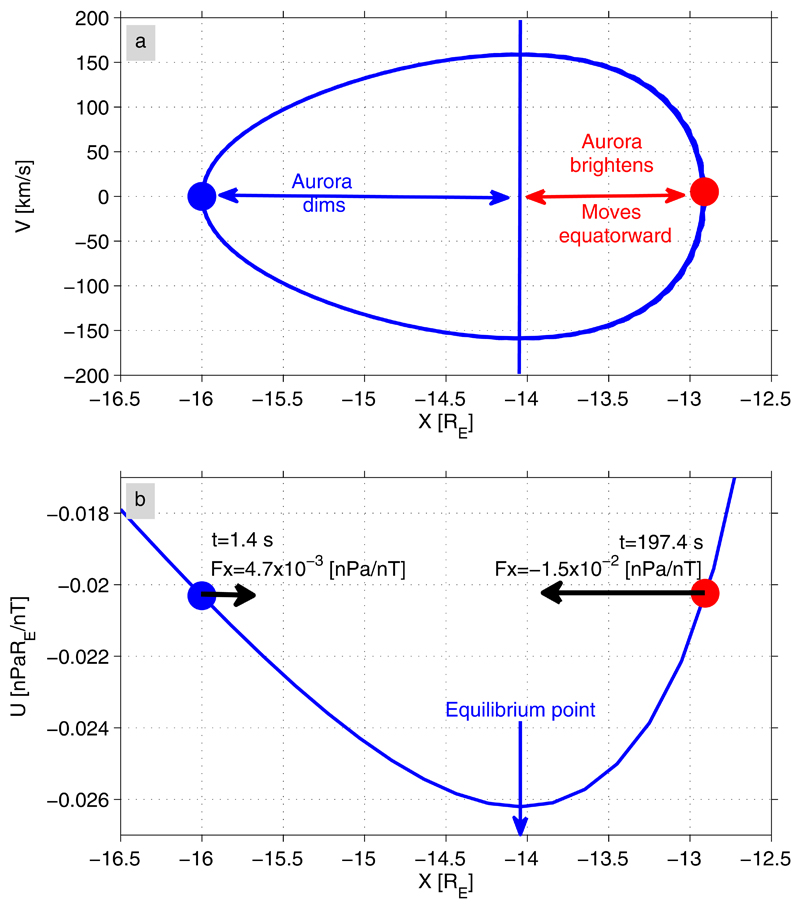
Recently, with the help of the thin filament approach ³², the oscillatory flow braking between 6:00 UT and 6:40 UT on 23 March 2009 was suggested to have occurred in an asymmetric potential in which the thin filament oscillations appeared to be anharmonic. Figure shows the theoretical predictions for THEMIS observations on 23 March 2009 around 6:21 UT: phase portrait of a thin filament oscillating anharmonically around its equilibrium position at X ≈ −14R_E (a) in the asymmetric potential well U (b). A movie in the auxiliary material shows one period of the thin filament oscillation on 23 March 2009 around 6:21 UT. The force per unit magnetic flux F_x (black arrows in Figure b) acting on the thin filament in its most earthward position (red solid circle at X ≈ −13R_E) appeared to be about three times larger than F_x in the filament’s most tailward position (blue solid circle at X ≈ −16R_E). Thus, the aurora brightened (field-aligned current enhanced) when the thin filament was earthward of its equilibrium position, and dimmed (field-aligned current depleted) when the thin filament was tailward of its equilibrium position.

Energy consumption rate

According to the above results, when the anharmonically oscillating magnetic flux tube is earthward of its equilibrium position, its interaction with the background plasma sheet is more dramatic: pressure and flux tube volume gradients become enhanced transiently. The plasma sheet currents appear transiently as a result of azimuthal displacement or bending of field lines in the tail and close at the ionospheric side through Pedersen currents across auroral arcs. The westward electrojet current, which is closed to itself, warping the upward and downward field-aligned currents, is the Hall current. Hence, during anharmonic oscillatory flow braking, flow burst kinetic energy may be damped and converted to Joule heating due to Pedersen conductance in the westward electrojet.

The ionospheric Joule heating is a part of the total energy dissipation that occurs during substorms ^{33, 34}. Using an empirical relation between the AE index and the Joule heating ³⁵ one can estimate the Joule heating for both hemispheres during the substorm under study (taking 0.6 GW for 1 nT in the average AE index during the substorm under study of about 50 nT) to be about 3 × 10¹⁰W.

Alternatively, the latitude-integrated precipitation rate near midnight for Kp=2 is about 1024 keV/(s-sr) for each half-hour bin in local time ³⁶. Multiplying by 4 to cover 2 hr in local time, by 2 to include both hemispheres, by π to integrate over a solid angle, and by 1.6 × 10⁻¹⁶ to convert energy units, we get about 4 × 10⁹W. Globally, Joule heating comes out to be of the order of twice the direct loss by precipitation; hence, the total dissipation would be ≈ 8 × 10⁹W. This is a little less than the above estimate, which is a reasonable correction due to statistical averaging. Let us compare these estimates with the dissipation rate that can be provided by the observed auroral arcs.

The Alfveńic wave impedance exerted on the current flow by mirror force is $R_W=\frac{{\mu }_0{R}_{E}L}{{\tau }_A{\Gamma }^2}\approx 1.4\Omega ,$ where McIlwain number L ≈ 11, Alfveńic transit time τ_A ≈ 45s, and Γ ≈ 1.2 characterizes the high-beta effect on the magnetic field ³⁷. From Figure b we get a current density for ionospheric field-aligned currents of about j_e,ion ≈ 100kA/(150km)² = 5µA/m². Note that the amplitudes of the alternating ionospheric currents are about ten times smaller (10% of the DC currents, Figures e and d). Knowing that the plasma sheet area where the field-aligned currents are generated is equal to or exceeds the area covered by THEMIS probes in the XY GSM plane, about $4R_E^2,$ one can obtain the field-aligned current density in the plasma sheet, about j_e ≈ 4nA/m². Knowing that the size of the region with enhanced (∇V × ∇P)_Z exceeded 3R_E (distance between P1,P2 and P3-P5), we find that the energy flux may reach ${\dot{W}}_{arc}=R_W{J}_{\parallel ,arc}^2\approx 0.35W/m^2,$ where $J_{\parallel ,arc}=j_e\times 3R_E\approx 0.5A/m.$ Hence, direct energy inflow into the arc with thickness ω_arc = 50km and length l_arc = 1000km is ${\dot{W}}_{arc}{\omega }_{arc}{l}_{arc}\approx 1.75\times {10}^{10}W.$

Another energy consumption estimate can be obtained from the potential drop ${\Phi }_{\parallel }=\sqrt{\frac{{\dot{W}}_{arc}}{K}}\approx 35kV,\text{where}K={\left(R_W{\omega }_{arc}^2\right)}^{-1}\approx 2.9\times {10}^{-10}S/m^2$ ³⁷. Following empirical expressions for conductivities ³⁸, we estimate the Hall-to-Pedersen conductivity ratio $s=\frac{{\Sigma }_H}{{\Sigma }_P}=0.45·{\Phi }_{\parallel }^{0.85}\approx 9.24$ and the Pedersen conductivity ${\Sigma }_{P,arc}=40S·\frac{{\Phi }_{\parallel }}{16+{\Phi }_{\parallel }^2}·\sqrt{\frac{{\dot{W}}_{arc}}{1mW/m^2}}\approx 21.1S.$ Hence, the Cowling conductivity ${\Sigma }_C=\left(1+\frac{s^2}{\widehat{\alpha }}\right){\Sigma }_{P,arc}\approx 1763S,\text{where}\widehat{\alpha }=1+\frac{1}{R_W{\Sigma }_{P,arc}}\approx \mathrm{1.034.}$ Note that such conductivity levels are found in the brightest substorm auroral elements, such as the surge horn ³⁹. The resulting tangential (westward) electric field in the ionosphere $E_t=\sqrt{\frac{R_W}{{\Sigma }_C}}{J}_{\parallel ,arc}\approx 14.1mV/m.$ The total energy consumption in the westward electrojet can be estimated as ${\dot{W}}_{tot}=2{\Sigma }_C{E}_t^2·{\omega }_{arc}·l_{arc}\approx 3.5·{10}^{10}W$ ³⁷, comparable to the above estimates of the direct energy inflow (≈ 1.75 × 10¹⁰W) and of the Joule heating (between 0.8 × 10¹⁰W and 3 × 10¹⁰W).

Whereas a substantial part of the magnetotail energy is brought with the magnetic flux ^{33, 34}, only a tenth of the total Joule heating (about 10⁹W) can be associated with the oscillating plasma sheet fast flows: in Figures e and d, the amplitudes of the alternating ionospheric currents are about 10% of the DC currents. The fastest flows (observed by P4 at 6:08 UT, not shown here) reached 600km/s. Knowing that BBFs occur in very localized channels up to 3R_E wide ^{11, 33}, that the plasma sheet thickness exceeded 3R_E (distance between P1 and P5 in the Z_GSM direction), and that the radial flow size exceeded 11R_E (earthward flow velocity at P4 integrated over 4min braking time between 6:03 UT and 6:07 UT), a minimal flow burst kinetic energy can be estimated as $W_{fb}=\frac{1}{2}{m}_p{n}_{p}99R_E^3\times {\left(600km/s\right)}^2\approx 8.1\times {10}^{11}J,$ where m_p is the proton mass, and n_p ≈ 0.1cm⁻³ is the proton number density. Thus, reasonably consistent with the presented THEMIS observations, W_fb can be dissipated by five arcs each providing a dissipation rate of ≈ 10⁹W over an arc lifetime (Figures e,f) of about three minutes.

Conclusions

The THEMIS space and ground magnetometer and all-sky imager observations analyzed above suggest that substorm current and auroral dynamics are controlled by magnetotail topology change and by produced and modulated during oscillatory braking fast flows at 10-14 Earth radii in the nightside magnetosphere. The auroral bulge appears to map in the flow braking region where the plasma sheet pressure and flux tube volume gradients are non-collinear. Two processes were identified to control the ionospheric current and auroral dynamics during the substorm. (i) A fast (35 km/s) tailward expansion of magnetotail dipolarization and then slower (13 km/s) inner plasma sheet restretching during substorm expansion and recovery phases cause faster (1.7 km/s) poleward, then slower (0.7 km/s) equatorward movement of the substorm auroral bulge. (ii) Plasma sheet parcels, oscillating anharmonically around their equilibrium position and building up stronger pressure and flux tube volume gradients earthward of this position, are responsible for discrete longitudinal auroral arcs within the bulge that move equatorward at a velocity of the order of 1 km/s. The observed auroral activity appears to consume sufficient energy to dissipate the released magnetotail energy.

Data availability

Time History of Events and Macroscale Interactions during Substorms (THEMIS) probes data is available from the Space Physics Data Facility of the Goddard Space Flight Center (http://cdaweb.gsfc.nasa.gov/) All Sky Imager data from THEMIS Mission Data website (http://themis.ssl.berkeley.edu/gbo/display.py); geomagnetic indices from the World Data Center for Geomagnetism, Kyoto (http://wdc.kugi.kyoto-u.ac.jp/); ground magnetometer data from the Canadian Array for Real Time Investigations of Magnetic Activity (http://www.carisma.ca), from Space Physics Data Facility of the Goddard Space Flight Center (http://cdaweb.gsfc.nasa.gov/), and from the SuperMAG consortium (http://supermag.jhuapl.edu). Upon request the authors will attempt to provide all other data supporting this study.

Figure 1. Ground observations of aurora and electric currents.

(a) Snapshot from three ASIs at Snap Lake (SNAP), Rankin Inlet (RANK), and Sanikiluaq (SNKQ) at 6:12:30 UT. Tiny yellow lines show local velocity of auroral substructures. (b) Current system structure on the ground: snapshot of EICs (arrows) and the SECS scaling factors (color: upward in reddish, and downward in bluish) at 6:12:30 UT, calculated using ground-based magnetometer array data. The footprints of the five THEMIS probes as predicted by the AM03 model are denoted by overplotted crosses (red for P1, green for P2, blue for P3, cyan for P4, and magenta for P5; see also zoom-in).

Figure 2. AM 03 model predictions of the magnetotail development near THEMIS probes.

(a) Locations of THEMIS probes P1-P5 on 23 March 2009 at 6:12 UT projected onto the noon meridian GSM plane. Evolution of the magnetic field lines between 6:02 and 6:42 UT and of the B_Z magnetic field component (b) for 6:03 and 6:18 UT and (c) for 6:21 and 6:40 UT according to the AM03 model are overplotted (see legends for color coding).

Figure 3. Overview of substorm parameters during substorm expansion and recovery phases.

(a) AL auroral electrojet index. (b) (∇V ×∇P)_Z, where P is plasma sheet pressure and flux tube volume V is calculated using formula (6) in ³¹. (c) Time-integrated average meridional auroral velocity at SNAP, RANK, and SNKQ (red curve), and geographic latitudes covered by the five THEMIS footprints, as predicted by the AM-03 model (pink area). (d) Total auroral luminosity from SNAP, RANK, and SNKQ. (e) Total upward and downward SECS scaling factors and horizontal EICs (see legend) on 23 March 2009 between 6:00 and 6:40 UT.

Figure 4. THEMIS space and ground observations on 23 March 2009 between 6:16 UT and 6:36 UT.

(a) Time-integrated oscillations of radial ion velocity V_R at P1 (red) and P2 (green), (b) time derivative of oscillations in V_R at P1 (red) and P2 (green), (c) (∇V × ∇P)_Z, where P is plasma sheet pressure and flux tube volume V is calculated using formula (6) in ³¹, (d) total upward J_up SECS scaling factors around Rankin Inlet, (d) total auroral luminosity from SNAP, RANK, and SNKQ, (e) meridional (red) and longitudinal (blue) auroral velocity components. Auroral speed and velocity components were averaged over field of view of RANK.

Figure 5. Theoretical predictions for THEMIS observations on 23 March 2009 around 6:21 UT.

phase portrait of a thin filament oscillating anharmonically around its equilibrium position at X ≈ –14R_E (a) in the asymmetric potential well U (b). Force per unit magnetic flux F_x is given in the most tailward (X ≈ –16R_E) and most earthward (X ≈ –13R_E) positions reached by the thin filament.