Microstructure and mechanics of healthy and aneurysmatic abdominal aortas: experimental analysis and modelling

Abstract

Soft biological tissues such as aortic walls can be viewed as fibrous composites assembled by a ground matrix and embedded families of collagen fibres. Changes in the structural components of aortic walls such as the ground matrix and the embedded families of collagen fibres have been shown to play a significant role in the pathogenesis of aortic degeneration. Hence, there is a need to develop a deeper understanding of the microstructure and the related mechanics of aortic walls. In this study, tissue samples from 17 human abdominal aortas (AA) and from 11 abdominal aortic aneurysms (AAA) are systematically analysed and compared with respect to their structural and mechanical differences. The collagen microstructure is examined by analysing data from second-harmonic generation imaging after optical clearing. Samples from the intact AA wall, their individual layers and the AAA wall are mechanically investigated using biaxial stretching tests. A bivariate von Mises distribution was used to represent the continuous fibre dispersion throughout the entire thickness, and to provide two independent dispersion parameters to be used in a recently proposed material model. Remarkable differences were found between healthy and diseased tissues. The out-of-plane dispersion was significantly higher in AAA when compared with AA tissues, and with the exception of one AAA sample, the characteristic wall structure, as visible in healthy AAs with three distinct layers, could not be identified in AAA samples. The collagen fibres in the abluminal layer of AAAs lost their waviness and exhibited rather straight and thick struts of collagen. A novel set of three structural and three material parameters is provided. With the structural parameters fixed, the material model was fitted to the mechanical experimental data, giving a very satisfying fit although there are only three material parameters involved. The results highlight the need to incorporate the structural differences into finite-element simulations as otherwise simulations of AAA tissues might not be good predictors for the actual in vivo stress state.

1. Introduction

An abdominal aortic aneurysm (AAA) is a local bulging of the abdominal aorta characterized by segmental weakening of the blood vessel. It is often accompanied by the development of an intraluminal thrombus [1,2]. In general, AAAs are clinically silent and without medical treatment AAAs may grow until rupture [3]. The event of rupture is associated with a significant mortality rate up to 85% [4]. However, the only current treatment of AAAs is elective surgical repair, which carries a high mortality risk, especially in older patients, and it does not necessarily improve survival [5]. Therefore, a reliable prediction of rupture risk for individual AAAs is of high relevance in order to assess when the risk of rupture justifies repair [6]. The decision for elective surgical repair is presently based on indicators such as the aneurysm diameter [7], which are more a rule-of-thumb than a scientific criterion, and therefore often unreliable, especially as they do not take into account individual AAA characteristics such as the tissue microstructure. When seen from a biomechanical point of view, rupture as a material failure occurs when the peak wall stress exceeds the local strength of the arterial wall [8]. As the material properties of the abdominal aorta depend largely on the complex network structure of elastin and collagen, which are the most important structural and primary load-bearing proteins in the arterial wall [9], changes in the structural components play a significant role in the pathogenesis of aneurysms. Hence, there is a need to develop a deeper understanding of the structure in the abdominal aorta and its ongoing (localized) reorganization during the disease process.

As acquisition of patient-specific three-dimensional images becomes easier, the utilization of finite-element (FE) analysis and biomechanics help to better understand the influence of structural changes on the mechanics. Related numerical models require physiologically determined material and structural parameters. Some mechanical data are available on healthy human abdominal aortas [10,11]. However, mechanical human tissue data coupled to structural information do not currently exist to be used for FE simulations neither for healthy nor for AAA tissues.

Biaxial extension tests on AAAs are documented in the literature (e.g. [12–14]), reporting anisotropic responses with stiffer behaviour in the circumferential direction. The studies [15–17] performed uniaxial extension tests until failure also reporting a stiffer circumferential direction. In addition, circumferential stiffening was reported in the studies [18–20], which measured the pressure modulus of AAA tissues. Contrary to these studies, isotropy was claimed by Raghavan et al. [21], who performed uniaxial extension tests. Following this assumption, uniaxial tension tests were also performed (e.g. [22–28]), testing only one direction of the specimens (either axial or circumferential).

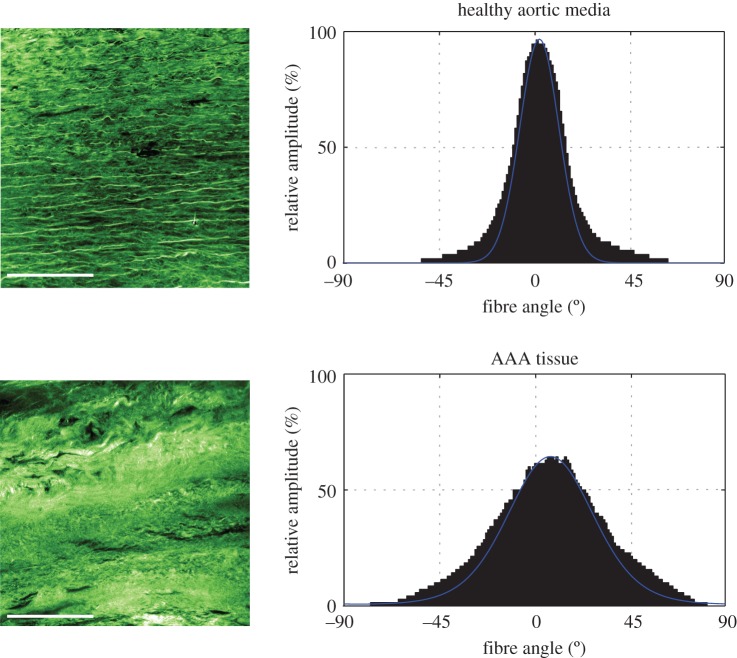
AAA simulations are often either based on linear material laws and the AAA tissue is often treated as an isotropic elastic material [29–32] or, if anisotropic material laws are used, simulations are based on structural data obtained from healthy tissues [16]. However, studies such as [33] have shown that a more advanced constitutive description of AAA tissues is critical for a proper prediction of AAA wall stresses. Additionally, we have identified substantial differences in the structure between healthy aortic tissues and tissues taken from AAAs. Especially the out-of-plane collagen dispersion in AAAs differs significantly in comparison with healthy tissue. Figure 1 shows representative second-harmonic generation (SHG) images of the collagen structure in a healthy abdominal aortic media and an AAA tissue taken from the middle portion of the wall thickness. The corresponding histograms of the angular dispersion of fibre angles clearly show a higher out-of-plane dispersion for the AAA tissue. This finding highlights the need for the incorporation of the AAA structure into related FE simulations as otherwise the numerical results may not be a good prediction of the in vivo state.

Figure 1.

Representative SHG images of the collagen structure in a healthy abdominal aortic media (above) and an AAA tissue taken from the middle portion of the wall thickness (below). Corresponding graphs show the angular dispersion (relative amplitude in %) of collagen fibre orientations, which is narrower for a healthy aortic media (smaller dispersion of fibres), when compared with AAA tissue (higher fibre dispersion). Scale bar, 100 µm. (Online version in colour.)

Although the pathogenesis and material properties of AAAs have been topics of several studies more recently [12,13,34–37], the specific events leading to AAA development still remain unclear. To the authors' knowledge, no biaxial mechanical data combined with the corresponding microstructure of both healthy (layer-specific) and aneurysmatic aortic tissues are yet available. To further increase the understanding and to improve rupture risk prediction it is necessary to study effects of localized wall changes (shown, for example, for cerebral aneurysms in [38]) by combining the microstructure with patient-specific mechanical data and systematically compare these changes with healthy abdominal aortic tissues. Such a knowledge can then be used to improve numerical models incorporating structure-based nonlinear material models, as was recently performed in [39] where the biaxial response of porcine aortic tissues was combined with the related microstructure identified using histological slices.

The aim of this study is to systematically analyse and compare the material properties of layer-specific healthy abdominal aortic tissue with tissue taken from AAA wall samples, by means of biaxial extension tests and their link with the three-dimensional microstructure using a combination of optical clearing, SHG imaging and subsequent automated quantification of the three-dimensional fibre dispersion and alignment. First, the used materials and methods are explained, involving tissue clearing and SHG imaging, biaxial stretching tests, a recently published material model used to capture the non-symmetric collagen fibre dispersion in arterial walls and the related mechanics, data fitting and the statistical analysis. Subsequently the results are presented, first the structural data and then the biaxial mechanical data. Differences between structural and material parameters are compared utilizing statistical tools, and correlations between these parameters are investigated. Finally, the results are discussed and put into context with the current literature.

2. Material and methods

Seventeen human abdominal aortas (AAs) with non-atherosclerotic intimal thickening from 7 women and 10 men (63 ± 11 (s.d.) years, range 45–84) were collected as intact tubes within 24 h of death and stored in 0.9% physiological saline solution at 4°C until testing. Additionally, 11 wall samples from (true) AAAs (69 ± 8 (s.d.) years; range 53–76; 1 woman, 10 men) were collected from open aneurysm repair at the anterior side at the Department of Vascular Surgery, Medical University Graz, Austria, and stored in Dulbecco's modified Eagle's medium at 4°C until testing. The AAA samples were mostly small pieces with the longitudinal direction marked by a surgical clip or suture.

2.1. Abdominal aorta and abdominal aortic aneurysm microstructure

2.1.1. Sample preparation

Intact aortic tubes were cut open along the longitudinal direction and small samples, approximately 15 × 5 mm in size, were acquired from both the healthy and the aneurysmatic specimens, with the longer side marking the longitudinal direction. Subsequently, the samples were cleared using a protocol according to [40]. First, the specimens were dehydrated by submerging them into a graded ethanol series, consisting of 50, 70, 95 and twice 100% concentrated ethanol solutions. Subsequently, the specimens were stored in 100% benzyl alcohol–benzyl benzoate (BABB) for at least 12 h after initially submerging them into a 1 : 2 solution of ethanol:BABB for 4 h. All steps were performed at room temperature. Whenever the thrombus, covering the corresponding aneurysmatic wall, was available, a small piece was fixed in 4% neutral-buffered formalin (pH 7.4), embedded in paraffin and prepared for histological investigations to determine the relative thrombus age according to [13].

2.1.2. Second-harmonic generation imaging

To identify the three-dimensional collagen structure of the samples, SHG imaging was performed at the Institute of Science and Technology in Klosterneuburg, Austria. An imaging set-up consisting of a Chameleon Titan Saphir laser (Coherent, Inc., USA) integrated into a TriM Scope II confocal microscope (LaVision BioTec GmbH, Germany) was used. The excitation wavelength was tuned to 880 nm and the detection of the backscattered signal was achieved using a gallium arsenide-phosphide detector and a BP 460/50 emission filter. Images (z-stacks, 3 µm steps and cross-section images in (x,z)-plane) were acquired using a Leica IMM CORR CS2 20× water immersion objective with a working distance of 0.68 mm.

2.1.3. Microstructural analysis of collagen fibre orientation

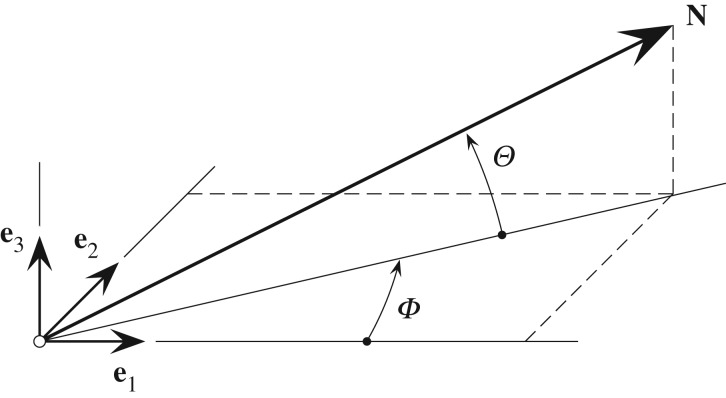
Morphological collagen data were extracted from three-dimensional images (z-stack) by combining Fourier power spectrum analysis and wedge filtering, as described in [40,41]. The analysis yielded discrete angular distributions of relative amplitudes, which resembled the fibre orientations. To describe a general fibre direction, a coordinate system characterized by the unit rectangular Cartesian basis vectors e₁, e₂ and e₃, as shown in figure 2, was used [42], with the unit vector N representing a general fibre direction in the (unloaded) reference configuration, defined by the two angles 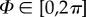and 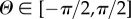. For a circular cylinder, e₁ is taken to be the circumferential direction and e₃ the radial direction, and therefore we refer to the angles Φ and Θ as the in-plane and out-of-plane angle, respectively.

Figure 2.

Unit vector N representing a general fibre direction defined by the two angles Φ and Θ with respect to rectangular Cartesian unit basis vectors e₁, e₂, e₃ [42].

The in-plane and out-of-plane collagen fibre orientations were fitted using a bivariate von Mises distribution 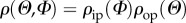for the probability density ρ of N (in-plane and out-of-plane dispersions are essentially independent [43]), with the particular choice [42]

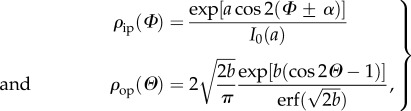2.1

where 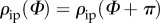and 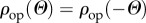describe the in-plane and out-of-plane dispersions, respectively. In (2.1), a and b are (constant) concentration parameters, i.e. fitting parameters, which define the shape of the von Mises distributions, I₀(a) is the modified Bessel function of the first kind of order 0 and α is the angle between the mean fibre direction and the circumferential direction e₁.

According to [42], we introduce the two scalar quantities κ_ip and κ_op which measure the in-plane and out-of-plane dispersion, respectively (they are used in the strain-energy function introduced in §2.3). Thus,

2.2

where 0 ≤ κ_ip ≤ 1 and 0 ≤ κ_op ≤ 1/2. If both concentration parameters a and b become infinite the collagen fibres are perfectly aligned.

Layer-specific thicknesses were measured from out-of-plane images using FIJI (http://fiji.sc/Fiji, Ashburn, VA, USA) [44]. They were used for the calculation of the dispersion parameters κ_ip and κ_op and the angle α of the intact AA wall. For example, the parameter κ_ip for the AA wall was calculated as the sum of the layer-specific κ_ip where the individual κ_ip was weighted with respect to the layer-specific thickness.

2.2. Abdominal aorta and abdominal aortic aneurysm mechanics

2.2.1. Sample preparation

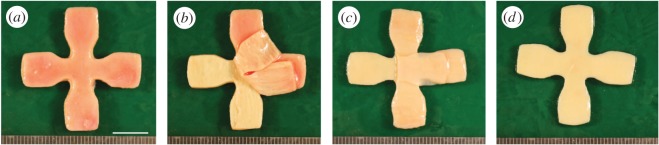
In regard to AA tissue, adjacent to the small samples which were prepared for SHG imaging, two squared samples with dimensions of 20 × 20 mm were cut out to obtain one composite patch (intact wall) and one medial patch (after the intimal and adventitial layers were peeled off), used for mechanical testing. In addition, a cruciform sample with dimensions of 35 × 35 mm adjacent to the other two samples was cut out with a punching tool so that a central region of the sample with dimensions of 5 × 5 mm remained (figure 3; the cruciform shape was designed using the FE method to minimize the inhomogeneity of the stress state in the central region [45]). Subsequently, intimal and adventitial patches required for testing were manually separated from the media. The layers were clearly distinguishable and minor fractions of the media could mostly be removed from the intima and the adventitia (figure 4).

Figure 3.

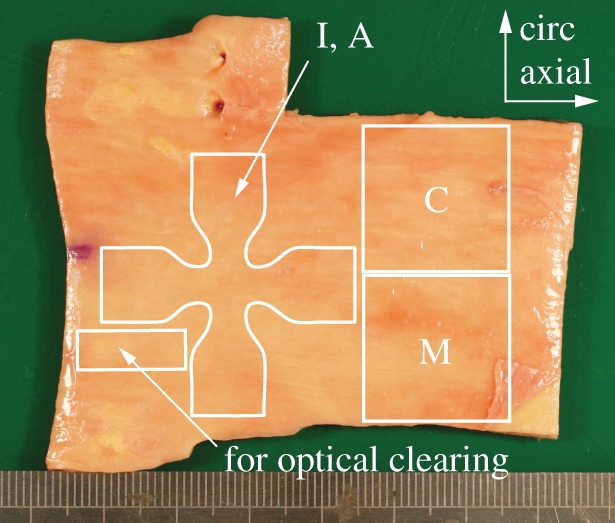
AA tissue showing contours of the samples, which were prepared from the specimen (I, intima; M, media; A, adventitia; C, composite). (Online version in colour.)

Figure 4.

Steps of preparing AA tissue for layer-specific biaxial testing: (a) cruciform sample of the intact wall; (b) separation of the adventitia (there are still some medial patches visible on the adventitia, which were peeled off later); (c) separation of the thin intimal layer; (d) medial layer left after the layer separation process. Scale bar, 10 mm. (Online version in colour.)

For the adventitia and the intima, cruciform samples had to be used because the sample thickness was very thin (less than 0.4 mm). Instead of piercing the hooks directly into the samples, the hooks were placed in sandpaper which was then glued to the arms of the samples. Especially by piercing the hooks directly into the intima we have frequently observed rupture even before mounting the sample into the testing machine. Intima and adventitia were thin enough to exhibit a homogeneous stress state in the central region of the cruciform sample. Intact wall and media sample were too thick (more than 0.7 mm) to be tested with the cruciform sample geometry, and hence were tested using the well-established squared geometry.

Similar to the healthy squared wall samples, a patch with dimensions of 20 × 20 mm was cut out from the AAA wall (sometimes two patches could be obtained). A clear identification of separable layers was impossible in most AAA samples, hence only the intact AAA wall was tested. The mean thickness of both AA and AAA samples was measured according to [46]. Subsequently, black tissue markers were applied by spraying on the surface of each sample generating a scattered pattern suitable for optical tracking.

2.2.2. Biaxial tensile tests

All samples were mounted in a biaxial testing device via hooked surgical sutures. The samples were submerged into a bath filled with 0.9% physiological saline solution and heated up to 37 ± 0.1°C. During testing normal and shear deformations were quantified according to [47], and it was found that negligible shear stresses were present throughout the testing.

A stretch-driven protocol was used for testing, and executed with a stepwise increase of 0.025 stretch until rupture, starting with 2.5% deformation. Each sample was tested using the following protocol for each stretch increment: λ_axial : λ_circ = 1 : 1, 1 : 0.75, 0.75 : 1, 1 : 0.5 and 0.5 : 1, where λ_axial denotes the stretch in the axial direction while λ_circ is the stretch in the circumferential direction. After each increase in stretch four preconditioning cycles were conducted and the fifth was then used for data recording and analysis. Throughout the test, the samples were loaded quasi-statically at a rate of 3 mm min⁻¹. It is worth noting that the used biaxial testing protocol covers a large range of deformations including the in vivo situation, and hence provides data for a unique set of material parameters. As the results, especially for the adventitial samples, were very sensitive to initial preloads, zero strain was defined at a tissue configuration under 0.005 N load.

2.3. Material model

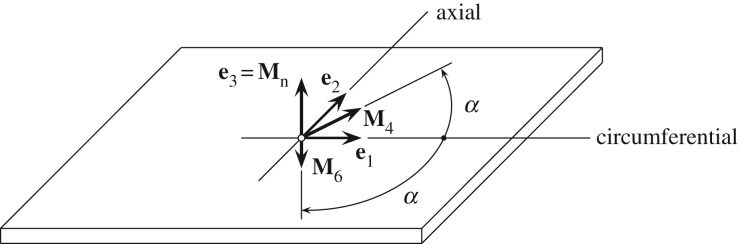
We introduce the deformation gradient F, the right Cauchy–Green tensor C = F^TF [48], and two symmetric fibre families with the (in-plane) mean fibre directions, i.e.

2.3

where the mean fibre directions M₄ and M₆ make an angle α with the circumferential direction e₁. In addition, we introduce the invariants I₁, I₄, I₆ and I_n according to

2.4

where M_n is a unit out-of-plane vector (figure 5).

Figure 5.

Sample with two symmetric fibre families with mean fibre directions M₄ and M₆, each making an angle α with the circumferential direction e₁. The normal direction to the plane is M_n [42].

To mathematically quantify the fibre dispersion, we use the generalized structure tensors H₄ and H₆, which describe the material behaviour [42], i.e.

2.5

where the constants A and B are

2.6

Assuming that the aorta can be modelled as a purely elastic, incompressible and fibre-reinforced material, the structure tensors H_i are incorporated into the decoupled strain-energy function Ψ according to

2.7

The strain-energy function Ψ_g represents the ground matrix, i.e.

2.8

where c is a parameter, and Ψ_fi represents the contribution of the two fibre families, i.e.

2.9

with the stress-like parameter k₁ > 0, the dimensionless parameter k₂ > 0 and the generalized invariants according to

2.10

which includes the mean fibre directions M_i in the form of the invariants I_i and the two dispersion parameters κ_ip and κ_op, as introduced in §2.1.3, in the form of the constants A and B.

The material model uses three structural parameters (κ_ip, κ_op, α) which can be determined by structural analysis (in this study using SHG images) and three material parameters (c, k₁, k₂), which are determined by fitting the model to the mechanical data (in this study to the data obtained from biaxial stretching tests).

2.4. Data fitting and statistical analysis

After the structural parameters have been determined as described above, fitting of the material model to the biaxial experimental data was performed. Data from all five testing protocols (1 : 1, 1 : 0.75, 0.75 : 1, 1 : 0.5, 0.5 : 1) in both axial and circumferential directions were fitted simultaneously, using the optimization toolbox lsqnonlin in Matlab (The MathWorks, Inc., MA, USA). As the structural parameters κ_ip, κ_op and α were known from structural analysis, and hence kept constant throughout the fitting procedure, the only three fitting parameters were c, k₁ and k₂. To evaluate the goodness of fit the coefficient of determination R² was used.

Our study resulted in three-dimensional distributions of amplitudes in 1° resolution, representing the in-plane and out-of-plane collagen dispersions in AAs and AAAs in combination with the corresponding mechanical data obtained from biaxial stretching tests, and yielded structural and material parameters for incorporation in a recently proposed micro-structurally motivated material model [42].

Values for the material parameters are reported as the medians and interquartile ranges (middle fifties), as we cannot assume a normal distribution due to the small sample cohort and outliers can affect the mean and standard deviation severely. Linear regression analysis was carried out to test possible correlations between the material and the structural parameters as well as patient data, using Pearson's correlation coefficient. Significant correlations between the median values of the material and structural properties were tested by using the Mann–Whitney U-test. Differences were considered statistically significant if the p-value was less than 0.05, corresponding to a 95% confidence. All statistical analysis was performed using Matlab.

3. Results

3.1. Study population

All 17 AA samples could be analysed for structural data. In total, mechanical testing succeeded for four intimal, nine medial, nine adventitial samples and seven samples for the intact AA wall. Additionally, all 11 samples of AAA walls could be analysed structurally and, except for one, succeeded in being tested biaxially. With the exception of one sample, all wall samples were covered by a thrombus, which was analysed to obtain its relative age. According to [13], all thrombi were in phase III (intermediate), in which the erythrocytes are disrupted and proteins are washed out of the fibrin network. The relative age is here defined by a number between 300 and 400 where these two numbers indicate the bounds to phase III and phase IV, respectively; hence a number closer to 300 corresponds to a relatively younger thrombus within phase III than a number closer to 400.

With the exception of one AAA sample, all aneurysms exhibited a maximum diameter of more than or equal to 55 mm, which is a size where intervention in men is typically advocated (or 50 mm in women, or if the maximal diameter increases more than 5–10 mm in 1 year) [7,49,50]; the average aneurysm diameter was 73 ± 20 mm, range 53–130 mm. Two samples (AAA-2, AAA-10) were collected from a ruptured aneurysm. The sizes of AAA-1 and AAA-4 were big enough to prepare two samples for the biaxial stretching tests. Hence, subsequently they are labelled as AAA-1.1, AAA-1.2, AAA-4.1 and AAA-4.2. For a summary of the patient information of all tested AAA samples, see table 1.

Table 1.

Patient information of all tested AAA specimens: age, gender (F, female; M, male), maximum diameter D, smoker, pack years, hypertension, aneurysm ruptured, thrombus, clinical signs of inflammation (inflam), diabetes and relative thrombus age (all in phase III according to [13]; a lower number refers to a younger thrombus).

patient no.	age (years)	gender	D (mm)	smoker y/n	pack years	hypertension y/n	ruptured y/n	thrombus y/n	inflam y/n	diabetes y/n	thrombus age
AAA-1	75	M	58	y	50	n	n	y	n	y	335
AAA-2	74	M	85	y	50	y	y	y	n	n	370
AAA-3	74	M	63	y	40	y	n	y	n	y	n.a.
AAA-4	55	M	85	y	40	y	n	y	y	n	320
AAA-5	74	M	66	y	20	y	n	y	y	y	350
AAA-6	53	M	53	y	50	y	n	y	n	y	380
AAA-7	72	F	55	y	20	y	n	n	n	n	320
AAA-8	76	M	70	y	25	y	n	y	n	y	n.a.
AAA-9	74	M	74	y	105	y	n	y	n	n	n.a.
AAA-10	61	M	130	y	90	y	y	y	n	y	n.a.
AAA-11	72	M	65	y	30	n	n	y	n	y	340

3.2. Structural data

3.2.1. Abdominal aorta

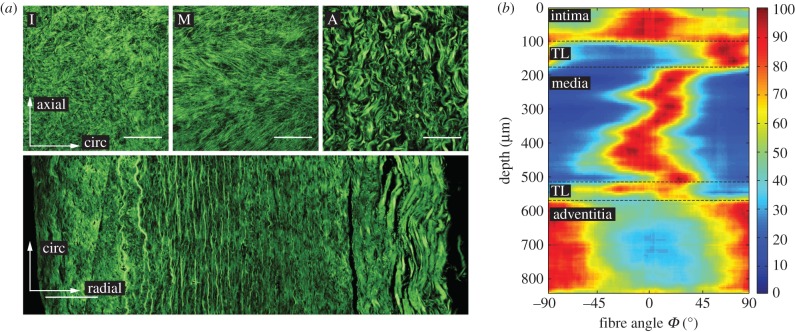
Figure 6a shows SHG images of a representative sample; the three images on the top display in-plane sections of the intima (I), media (M) and adventitia (A), while on the bottom an image through-the-thickness is displayed. Consistent with [43], the healthy AA consists of three distinguishable layers with a carpet-like structure in (I) and two families of fibres in (M), more oriented towards the circumferential direction, while (A) shows wavy and thicker fibre bundles more oriented towards the axial direction. The image through-the-thickness displays the intima on the left, then a transition layer (TL) and the highly oriented media, and then, after another TL, the wavy collagen of the adventitia.

Figure 6.

Layered structure of a representative healthy abdominal aorta. (a) Three SHG images on the top showing in-plane sections of the intima (I), media (M) and adventitia (A), while on the bottom an image through-the-thickness is displayed. Scale bar, 100 µm. (b) Intensity plot showing collagen fibre orientation and dispersion through the depth of the aortic wall starting with the intima, followed by a transition layer (TL) around the location of the membrana elastica interna, then the media, followed by another TL around the location of the membrana elastica externa, and finally the adventitia—dark red depicts no dispersion and blue relates to no fibres. (Online version in colour.)

The intensity plot of figure 6b depicts the collagen fibre orientation and dispersion through the aortic wall. A fibre angle of 0° denotes the circumferential direction, whereas 90° denotes the axial direction. Dark red depicts no dispersion, whereas blue shows no fibres. The images were taken starting from the intimal side. Hence, the intima can be seen in the first 100 µm in the intensity plot, showing a rather strong dispersion around the circumferential direction. That is followed by a TL observed as a (rapid) orientation change of collagen fibres towards the axial direction around the location of the membrana elastica interna, which then changes back to the circumferential direction in the media. The images show two counter-rotating fibre families around the circumferential direction. Subsequently, another TL around the location of the membrana elastica externa is reached, displaying a rather smooth transition of thinner medial collagen to thicker wavy collagen fibre bundles in the adventitia, appearing in two fibre families and being oriented more towards the axial direction.

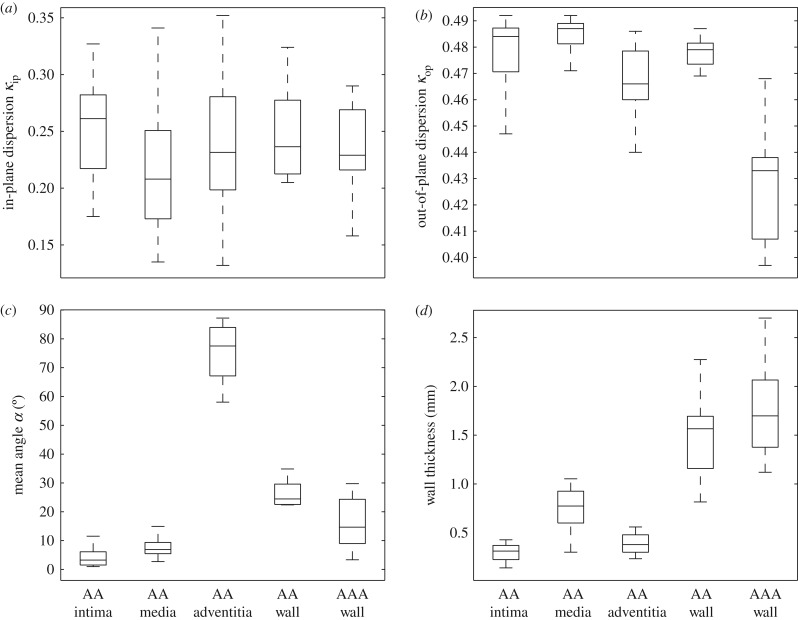
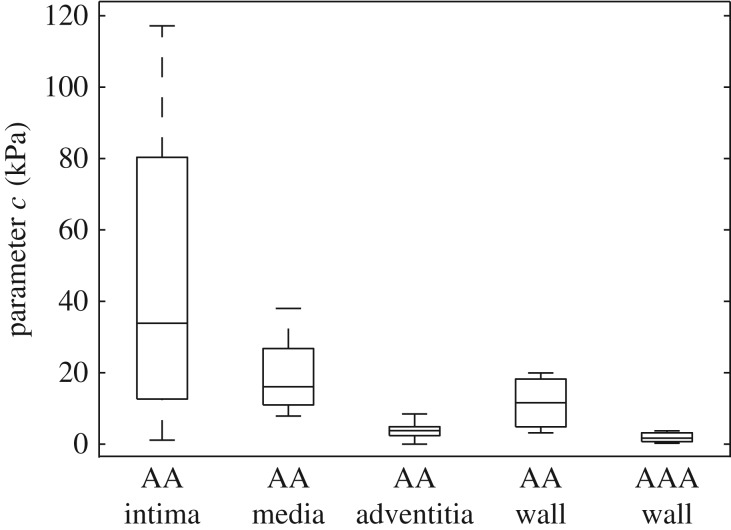
Although the tissues were not loaded, the fibres displayed a highly organized structure both in the tangential plane of the aorta and through the thickness of the wall, which enabled the determination of structural data, i.e. the dispersion parameters κ_ip and κ_op, and the angle α between the mean fibre direction and the circumferential direction which were averaged over the thickness of the separate layers. The structural parameters for the individual layers and for the intact wall are summarized in table 2. The out-of-plane dispersion κ_op was rather low in all three healthy layers. Especially for the intima and media the fibres were highly aligned, with a median for κ_op close to 0.5 (0.484 ± 0.019 and 0.487 ± 0.008, respectively). The wavy structure of the collagen fibres in the adventitia in the unloaded configuration resulted in a slightly higher out-of-plane dispersion, i.e. κ_op = 0.466 ± 0.020. The fibre families in the media were aligned closer to the circumferential direction than reported in [43], with a median angle of α = 6.91° ± 4.4°, while the fibre families in the adventitia were aligned closer to the axial direction with α = 77.53° ± 17.0°. For a summary of the dispersion parameters κ_ip, κ_op and the angle α in the form of box-and-whisker plots, see figure 7a–c, while figure 7d shows the thicknesses of the intact AA wall and each individual layer, with a mean ratio 20 : 49 : 31 for intima:media:adventitia, which is consistent with [43].

Table 2.

Structural parameters (κ_ip, κ_op, α) for the intima, media, adventitia and the intact wall of the abdominal aortas determined from SHG images; n indicates the number of samples.

	intima		media		adventitia		intact wall
	median	[Q1;Q3]	median	[Q1;Q3]	median	[Q1;Q3]	median	[Q1;Q3]
κip	0.261 (n = 7)	[0.214; 0.283]	0.208 (n = 17)	[0.165; 0.255]	0.232 (n = 16)	[0.192; 0.282]	0.237 (n = 7)	[0.212; 0.287]
κop	0.484 (n = 17)	[0.468; 0.488]	0.487 (n = 17)	[0.481; 0.489]	0.466 (n = 17)	[0.459; 0.479]	0.479 (n = 17)	[0.473; 0.482]
α	3.25° (n = 7)	[1.09; 6.13]	6.91° (n = 17)	[5.269; 9.715]	77.53° (n = 16)	[67.04; 84.02]	24.46° (n = 7)	[22.45; 30.18]

Figure 7.

Box-and-whisker plots of the structural parameters and the wall thickness for the AA, the individual layers, and for the AAA wall: (a) in-plane dispersion parameter κ_ip; (b) out-of-plane dispersion parameter κ_op; (c) mean fibre angle α; (d) wall thickness. AAA wall data refer to §3.2.2.

3.2.2. Abdominal aortic aneurysm

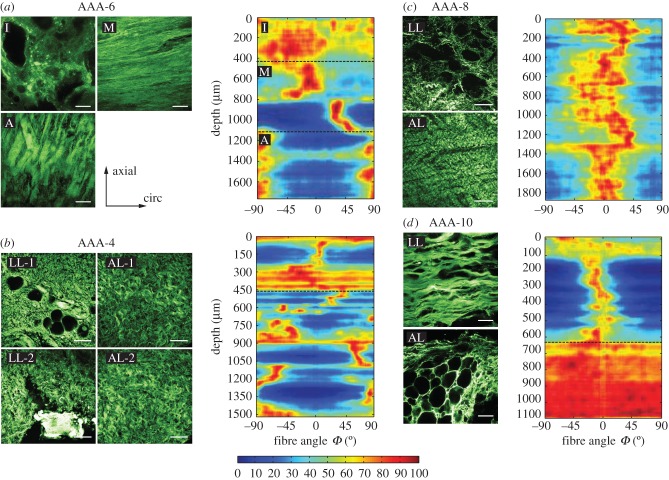
Within the AAA wall, specific layers could not be identified, except for sample AAA-6, and the characteristic wall structure, as visible in healthy abdominal aortic walls with three distinct layers, was not present. Even in samples without atherosclerotic alterations the structure was remarkably different from those obtained from AAs. By comparing the tissue samples with each other a substantial variability in fibre architecture, fibre diameter and waviness could be identified, even within the same AAA sample. In general, most samples showed a degenerated luminal layer with calcification and sometimes small fat cells, and thin straight struts of collagen oriented more towards the circumferential direction. Towards the abluminal side, these struts thickened, but were still oriented more towards the circumferential direction. In addition, cystic medial degeneration could be seen, including larger adipocytes. For the structural analysis, only those images were considered which did not show calcification or adipocytes, as otherwise the averaged dispersion parameter values would have been distorted.

Sample AAA-6 exhibited a strikingly healthy architecture, had the smallest diameter (53 mm) and was covered by the oldest thrombus of all samples. It showed a rather isotropic intimal side, two fibre families oriented more towards the circumferential direction in the media and an adventitia-like structure with highly aligned fibres oriented more towards the axial direction (figure 8a). In-plane images of the intima also showed small fat cells and calcification at the luminal side (not considered for structural analysis), explaining the rather isotropic structure seen in the intensity plot at the top until a depth of about 400 µm (figure 8a), while the media showed straight collagen fibres resulting in high and narrow intensities in the intensity plot (depth between 400 and 1100 µm). Remarkably, the collagen fibres in the abluminal layers of AAAs lost their waviness and exhibited rather straight and thick struts of collagen. Samples AAA-1, AAA-3, AAA-5, AAA-7 and AAA-11 exhibited a similar collagen structure throughout the thickness as seen in the adventitia of sample AAA-6, having lost the layered structure. Samples AAA-1 and AAA-7 showed alternating fibre families with a mean fibre angle α = ±26° and α = ±29.74°, respectively, whereas the other samples were oriented closer to the circumferential direction, also exhibiting alternating fibre families.

Figure 8.

SHG images and intensity plots for AAA samples. (a) Layered structure of sample AAA-6 (I, intima; M, media; A, adventitia) which was the only AAA sample to exhibit a layer-specific character. The intensity plot shows three distinct layers—a rather calcified intima, two fibre families in media and adventitia. (b) Structure of luminal layer (LL) and abluminal layer (AL) of two patches taken from adjacent locations (-1, -2) of sample AAA-4 displaying differences. The lower left image (LL-2) shows wavy collagen fibres and calcification. The first 450 µm in the intensity plot show a highly disturbed structure followed by an adventitia-like structure with two alternating fibre families. (c) Collagen structure of sample AAA-8 in LL and AL. The intensity plot shows collagen preferably oriented towards the circumferential direction throughout the wall. (d) Ruptured sample AAA-10 containing an LL with a highly oriented collagen structure and a significant number of adipocytes towards the AL side. The intensity plot shows a collagen structure highly oriented towards the circumferential direction followed by a rather isotropic AL. All intensity plots start at the top with the LL. Scale bar, 100 µm. (Online version in colour.)

The two patches taken from adjacent locations of sample AAA-4 showed an intact abluminal layer (AL) similar to a healthy adventitia layer (figure 8b). However, no media was visible as the wavy collagen fibres were infiltrated with plaque and adipocytes. The upper left image (LL-1) in figure 8b (where LL stands for luminal layer) shows bright ‘stains’ representing a rather degenerated collagen structure. The lower left image (LL-2) shows an adjacent region in the same LL, exhibiting a different structure with wavy collagen fibres and calcification. The first 450 µm in the intensity plot show a disturbed structure merging into two alternating fibre families.

The AL of sample AAA-8 showed thickened collagen struts still wavy but oriented more towards the circumferential direction (figure 8c). Towards the LL, the fibres became thinner and looked more like in a healthy adventitia, merging into a disturbed collagen structure. The intensity plot shows fibres preferably oriented towards the circumferential direction throughout the wall, ending with some more anisotropic structure, resembling the degeneration at the luminal side. Both ruptured samples (AAA-2 and AAA-10) showed a significant amount of cystic medial degeneration, infiltrated with adipocytes in the AL, preceded by a highly organized collagen structure in the LL oriented more towards the circumferential direction (figure 8d). The AL is rather isotropic as can be seen from the intensity plot. Sample AAA-9 showed a similar structure to the two ruptured samples.

The structural parameters for the AAA wall determined from SHG images are summarized in table 3 and illustrated in the form of box-and-whisker plots in figure 7a–c, while figure 7d shows the AAA wall thickness. The structural parameters for the samples AAA-1 and AAA-4 were only taken from one sample. All AAA samples with the exception of sample AAA-10, which is the ruptured one, showed a similarly high alignment of collagen fibres with a median of κ_ip = 0.229 ± 0.057, and the in-plane dispersion did not show any statistical difference with respect to intact AA walls, compare with tables 2 and 3. The out-of-plane dispersion was significantly higher (p < 0.0001) in AAA samples when compared with healthy (control) samples, as clearly visualized in figure 7b (lower dispersion parameter κ_op for AAA walls). In addition, figure 9 shows the collagen structure of three AAA samples through the thickness indicating a higher out-of-plane dispersion when compared with the layered structure of a healthy abdominal aorta, see, for example, the image on the bottom of figure 6a. Finally, when compared with intact AA walls, AAA samples showed a smaller mean fibre angle α (p = 0.06) (table 2).

Table 3.

Structural parameters (κ_ip, κ_op, α) for the AAA wall determined from SHG images.

patient no.	κip	κop	α
AAA-1	0.290	0.397	26.00
AAA-2	0.229	0.438	3.33
AAA-3	0.276	0.398	13.97
AAA-4	0.223	0.413	24.33
AAA-5	0.261	0.438	9.05
AAA-6	0.202	0.468	9.22
AAA-7	0.216	0.428	29.74
AAA-8	0.265	0.407	8.98
AAA-9	0.207	0.464	18.41
AAA-10	0.158	0.461	7.87
AAA-11	0.269	0.438	15.37
median	0.229	0.438	13.97
[Q1; Q3]	[0.209; 0.268]	[0.409; 0.455]	[9.998; 22.85]

Figure 9.

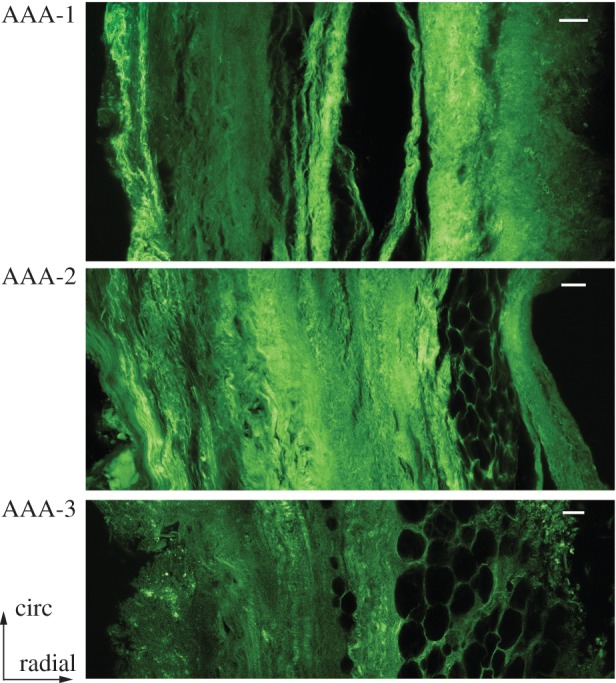
Collagen structure in the circumferential/radial plane of samples AAA-1, AAA-2 and AAA-3 indicating high dispersion of collagen fibres. Luminal side: left; abluminal side: right. Scale bar, 100 µm. (Online version in colour.)

3.3. Biaxial mechanical data

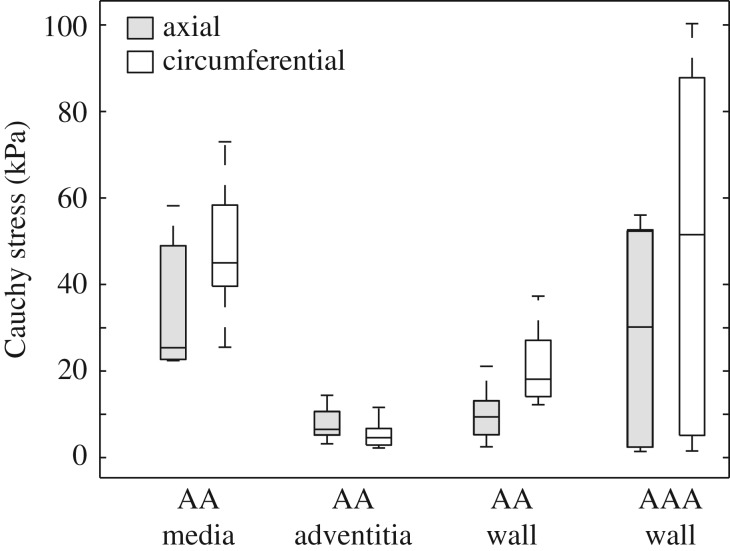
The material parameters (c, k₁, k₂) for the AA samples and the AAA walls are summarized in tables 4 and 5, respectively, whereas the associative structural data, which were used for fitting the individual samples, are summarized in tables 2 and 3. The median of R² was 0.95 ± 0.05, 0.98 ± 0.03, 0.95 ± 0.12, 0.96 ± 0.04 and 0.93 ± 0.03 for the intima, media, adventitia, intact AA wall and AAA wall, respectively. In addition, figure 10 shows box-and-whisker plots of the Cauchy stress at 1.15 stretch in the axial and circumferential directions for the AA and for the AAA wall; stresses in the circumferential direction of the walls were always higher compared with the axial direction.

Table 4.

Material parameters (c, k₁, k₂) and related coefficient of determination (R²) for the intima, media, adventitia and the intact wall of the abdominal aortas determined from biaxial stretching tests; n indicates the number of samples.

	intima (n = 4)		media (n = 9)		adventitia (n = 9)		intact wall (n = 7)
	median	[Q1; Q3]	median	[Q1; Q3]	median	[Q1; Q3]	median	[Q1; Q3]
c (kPa)	33.86	[6.88; 98.76]	16.08	[10.34; 30.52]	3.77	[2.18; 4.97]	11.59	[4.13; 19.93]
k1 (kPa)	7.79	[4.90, 55.00]	11.68	[2.32; 22.81]	0.36	[0.06; 1.70]	2.66	[1.15; 11.64]
k2 (−)	139.1	[41.95; 243.31]	7.18	[2.94; 22.78]	45.88	[21.10; 69.85]	19.25	[9.93; 26.06]
R2	0.95	[0.93; 0.98]	0.98	[0.07; 0.99]	0.95	[0.84; 0.97]	0.96	[0.94; 0.97]

Table 5.

Material parameters (c, k₁, k₂) and related coefficient of determination (R²) for the AAA samples determined from biaxial stretching tests. Samples AAA-2 and AAA-10, the two which originate from the ruptured aneurysms, were considered as outliers due to the extreme wall stiffness, and hence were excluded from the statistical analysis of the material parameters.

patient no.	c (kPa)	k1 (kPa)	k2 (−)	R2
AAA-1.1	1.08	0.45	53.33	0.90
AAA-1.2	1.50	1.71	157.89	0.99
AAA-2	0.50	26.94	220.70	0.68
AAA-3	0.23	2.94	28.54	0.89
AAA-4.1	1.66	5.82	99.91	0.98
AAA-4.2	0.54	8.00	100.07	0.94
AAA-5	3.72	2.73	123.52	0.90
AAA-6	3.39	5.49	61.00	0.56
AAA-7	2.47	0.92	12.49	0.97
AAA-8	0.57	4.02	1.44	0.99
AAA-10	600.60	5.70	3315.60	0.76
AAA-11	2.56	0.75	47.33	0.93
median	1.58	2.84	57.17	0.94
[Q1; Q3]	[0.57; 2.56]	[0.92; 5.49]	[28.54; 100.07]	[0.90; 0.98]

Figure 10.

Box-and-whisker plots of the Cauchy stress at 1.15 stretch in the axial and circumferential directions for the AA (media, n = 6; adventitia, n = 6; wall, n = 7), and the AAA wall (n = 7).

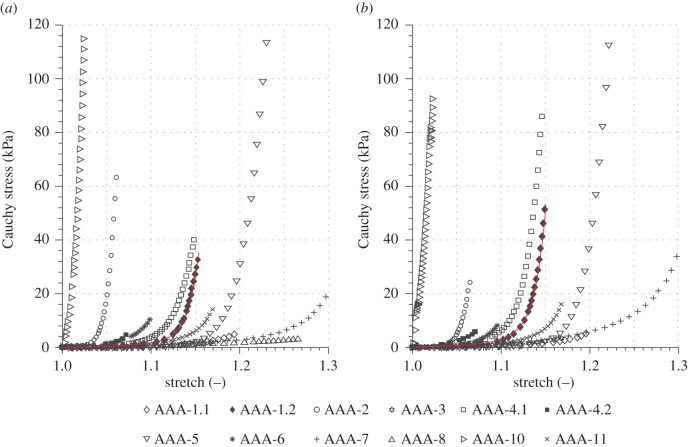
Within the healthy group the intima showed a relatively short toe region with a rapid stiffening at a low stretch (λ ∼ 1.025), as also documented in [11], whereas the adventitia was rather compliant (c = 3.77 ± 2.79, k₁ = 0.36 ± 1.64), stiffened at higher stretches and displayed a significantly higher k₂ value in comparison with the media and the intact wall (λ ∼ 1.2, k₂ = 45.88 ± 48.75). Therefore, only one intima sample, not shown in figure 10, reached a stretch of 1.15. In regard to AA walls, the parameter c for AAA walls was significantly lower (p = 0.0004; tables 4 and 5 and figure 11). However, the dimensionless parameter k₂ with 57.17 ± 71.53, resembling the exponential stiffening of the loading curves due to the collagen fibres, was significantly higher than for AA walls (k₂ = 19.25 ± 16.13, p = 0.025). Interestingly, by comparing the adventitia of AAs with AAA tissue the k₂ value was not significantly different between the two groups (p = 0.40); however, AAA tissue differed significantly in both the c value (p = 0.028) and the k₁ value (p = 0.022) with respect to the adventitia of AAs. Figure 12 shows equibiaxial mechanical responses (stretch ratio of 1 : 1) of 12 AAA patches.

Figure 11.

Box-and-whisker plots of the parameter c for the individual layers and the whole wall of the AA, and for the AAA wall.

Figure 12.

Cauchy stress versus stretch behaviour of 12 AAA patches obtained from equibiaxial mechanical tests indicating a substantial variability in the mechanical response: (a) axial direction; (b) circumferential direction. The two samples AAA-2 and AAA-10 originate from ruptured aneurysms. The red curves depict an exemplary model fit to sample AAA-1.2. (Online version in colour.)

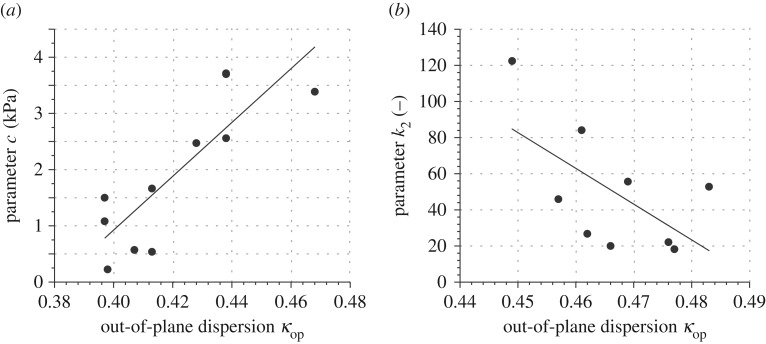
Linear regression analysis was carried out to test for possible correlations between material and structural parameters, and patient data. Two cases were identified to correlate significantly (figure 13).

Figure 13.

Significant correlation of material with structural parameters: (a) parameter c in model (2.8) with out-of-plane dispersion parameter κ_op for AAA tissues; (b) parameter k₂ in model (2.9) with κ_op for AA adventitial tissues.

4. Discussion

To the authors' knowledge, this is the first study to provide structural data for healthy human (layer-specific) abdominal aortic samples and AAA walls in combination with mechanical data for studying the physiology and pathology of human aortas such as AAAs. We have shown that AAA tissues, in contrast to tissues obtained from healthy AAs, display a substantial variability in fibre architecture, fibre diameter and waviness and in material properties. A combination of optical clearing and SHG imaging was used to analyse the three-dimensional microstructure without damaging the tissue structure due to cutting, and the mechanical data were obtained from biaxial stretching tests. The used material model that takes account of the identified non-symmetric arrangement of collagen fibres (tables 2 and 3), documented in [42] and reviewed in §2.3, was capable of providing good fits for the samples of the AA, their individual layers and the AAA samples (tables 4 and 5), although there are only three material parameters involved. A novel set of structural and material parameters for the material model [42] is provided to be used in FE simulations.

In the following sections, we discuss the obtained structural and mechanical data of the two groups of tissues.

4.1. Structural data

A human AA with non-atherosclerotic intimal thickening is composed of three layers, which can clearly be distinguished and dissected. The obtained structural data were similar to those documented in [43]; however, the angles α between the mean fibre direction and the circumferential direction, especially in the media, were smaller than those reported in [43] where polarized microscopy was used in combination with a universal stage. This is most probably due to the different methodology used: in this study, the aortic wall was not pre-stretched, the structures of the tissues were analysed in the (unloaded) reference configuration and SHG imaging was used. For a short and recent summary of imaging modalities that can reveal the fibrous microstructure including an original investigation of optical polarization tractography to visualize the fibre structure in the bovine carotid artery, see [51].

The study [37] also performed an analysis of AAA collagen fibre dispersion in order to gain structural data in the unloaded reference configuration. However, that study has some drawbacks, which we could avoid. For example, the measurements were performed manually during histological imaging using polarized light microscopy, which requires embedding the sample in paraffin and mechanical sectioning and staining with picrosirius red so that only a very small thin slice of a fixed sample can be imaged. Our approach has the advantages that tissue clearing does not change the dimensions of the sample (shown in [40]), in contrast with [37], in which a necessary back-calculation to the reference configuration of the collagen orientation due to thickening of the sample after fixation was reported. We did not have to cut and stain the samples to prepare histology, which may be accompanied by several artefacts such as shrinkage, distortion, overlapping regions and holes due to calcification just to name a few [52]. In this study, we were able to attain a continuous three-dimensional dispersion of the collagen fibre orientations throughout the entire thickness. Finally, our study protocol enabled a systematic comparison of tissues obtained from healthy AA and AAA, and we conclude that the out-of-plane dispersion of collagen was significantly higher in AAA samples than it was in healthy AAs.

AAA wall samples showed a large variation in tissue composition including plaque, cystic medial necrosis and adipocytes, consistent with findings reported in [53]. Except for sample AAA-6, the typical layered structure of AA walls, as analysed previously (e.g. [40,43]), could not be detected. This observation is in accordance with the study [36], which shows a complete loss of the normal architecture and loss of the distinction between medial and adventitial collagen organization. Albeit the small sample size, we hypothesize that collagen fibres reorient towards the circumferential direction with disease progression, as the angle towards the circumferential direction was lower in AAA wall samples compared with samples obtained from AA walls. This is in accordance with the studies [12,14,17,54], which reported a pronounced increase in the circumferential stiffness for AAA tissue when compared with AA tissue. As collagen turnover is governed by local stress and strain rates [9], supra-physiological stresses in AAAs may be responsible for the collagen fibre realignment towards the circumferential direction. Although in our study the samples were not pre-stretched, fibres in AAA samples often appeared straight and much thicker than collagen in healthy samples.

The examination of two patches (AAA-4.1, AAA-4.2) taken from adjacent locations of sample AAA-4, figure 8b, showed different structural characteristics and some variation in the mechanical behaviour. As the significant influence of the collagen structure on the mechanics of healthy and diseased collagenous tissues has long been known, the different microstructure in adjacent regions of a sample may explain the diversity in local AAA stress states [3,14,24,55,56]. We found no significant influence of the aneurysm diameter on the structural and material parameters, which strengthens the hypothesis that the diameter criterion is insufficient, which is in line with previous findings (e.g. [16,35]).

4.2. Mechanical data

In regard to the mechanical data of AA samples, with a mean age of 63 years, it is the intima which exhibited a rather stiff mechanical behaviour. In healthy young individuals, however, the intima is a single layer of endothelial cells resting on a thin basal membrane. It thickens (and stiffens) with age (arteriosclerosis) so that the mechanical contribution of the intima on the overall stiffening of the wall is significant. Comparing our results of the intact AA wall with the behaviour reported in [10], we find a similar behaviour. Our peak stretches are in the same range as reported in [10], and the overall mechanical behaviour was stiffer in the circumferential direction for all samples. Unfortunately, in [10] a phenomenological Fung-type strain-energy function was used, which hampers the comparison of the mechanical response. Although there are only three material parameters involved, the model agrees very well with the experimental data of all samples, whereby the three structural parameters were fixed during the fitting process.

A significant difference in the parameter c, relating to the ground matrix, and k₂, relating to the stiffness of the collagen fabric, between healthy and diseased tissues was observed. The median parameter c is significantly lower in AAA tissue in comparison to AA wall samples, indicating a minor isotropic contribution to the strain-energy function for AAAs. We also know that the elastin content, which is mainly related to the ground matrix, decreases significantly with increasing AAA diameter (e.g. [57]), which is depicted by the low c values found in the present study. In addition, Vande Geest et al. [12] discussed a decrease in the initial slope of AAA samples compared with AA wall samples, which also corresponds to our findings of a decreased parameter c. The significantly higher value of the parameter k₂ indicates a stiffer behaviour of the AAA tissues when compared with healthy AA wall samples, which was also reported in [12,16]. However, our samples showed a rather compliant behaviour at low stretches and a rapid stiffening at higher stretches, which, to the authors' knowledge, was not yet discussed in previous studies. The present findings of straight and parallel collagen fibres in AAA samples is also along the findings in [36], which demonstrate a deposition of aggregated parallel collagen sheets in AAAs that appear rigid (e.g. fig. 2e in [36]).

As can be seen from figure 12, the biaxial mechanical AAA behaviour shows a wide variability, which underlines the importance of patient-specific modelling to assess rupture risk. Any difference in the finding to previous studies could be due to this variability, which again highlights the need to acquire structural data in combination with mechanical data in each individual case. The fits of the used material model to the experimental data were very good throughout all AAA samples, with the exception of sample AAA-6 (R² = 0.56). As the only sample, AAA-6 showed a layered structure, similar to a healthy AA. The bad fit of sample AAA-6 in comparison to all other samples, in which the typical layered structure was lost, supports the hypothesis that most AAA walls can be captured by one homogeneous material model. However, healthy AAs need to be modelled by three layers with specific parameters.

Despite the small number of available samples, we report significant correlations between material and structural parameters and patient data, which resulted in two cases, figure 13: (i) parameter c, relating to the ground matrix, showed a positive correlation with the out-of-plane dispersion parameter κ_op for AAA tissues, with a Pearson correlation coefficient of r = 0.836; (ii) parameter k₂ correlated with a negative correlation of r = –0.612 with κ_op for AA adventitial tissues. Although all layers and parameters were investigated for possible correlations only these two cases showed statistically significant correlations.

4.3. Concluding remarks

This study documents a novel parameter set consisting of microstructural three-dimensional collagen orientation and dispersion linked to mechanical data of the same specimen obtained from biaxial stretching tests. To the authors' knowledge, it is the first biaxially determined dataset which is linked to the three-dimensional collagen structure of AAs, their individual layers and of AAA wall samples. Our results highlight the need to incorporate the significantly different AAA wall structure into continuum models as the structure and the mechanical response differ remarkably from healthy AA walls. Otherwise, numerical results from FE simulations for AAA tissues, often based on parameters for healthy aortic tissue, are not a good predictor of the in vivo stress state or the risk of rupture. Compared with previous studies attempting to identify distributed collagen fibre orientations in artery walls our method yields a continuous distribution of the collagen fabric throughout the thickness without destroying the tissue, therefore allowing also an investigation of specific regions of interest. Additionally, we analysed and compared the structure and mechanics of samples obtained from healthy AAs with AAA samples which allowed new insights. In particular, the out-of-plane dispersion of collagen for AAA tissues was significantly higher than in healthy AAs. The mechanical and structural data showed not only a rather large variability between the samples but also in adjacent regions of the same sample. This leads to the conclusion that the disease progression in AAAs is a highly localized process, leading to variations in structure in adjacent regions of the same AAA wall. Owing to the substantial variability in structure and mechanics, it is clear that a ‘one-fits-all’ criterion such as the diameter criterion is not good enough.

In the future, more effort should be made to better investigate collagen fibre undulation and thickness measurement, as straight and thick collagen struts were spotted on several samples throughout the thickness. Improved imaging of the aorta may provide in vivo information regarding aortic geometry, structure and anisotropy, and when combined with a hemodynamic assessment it may have the potential to identify patients at high risk and to access rupture risk individually thereby facilitating prophylactic treatment of aneurysms.

Ethics

Both the use of autopsy and AAA materials from human subjects were approved by the Ethics Committee of the Medical University of Graz (27–250 ex 14/15).

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.