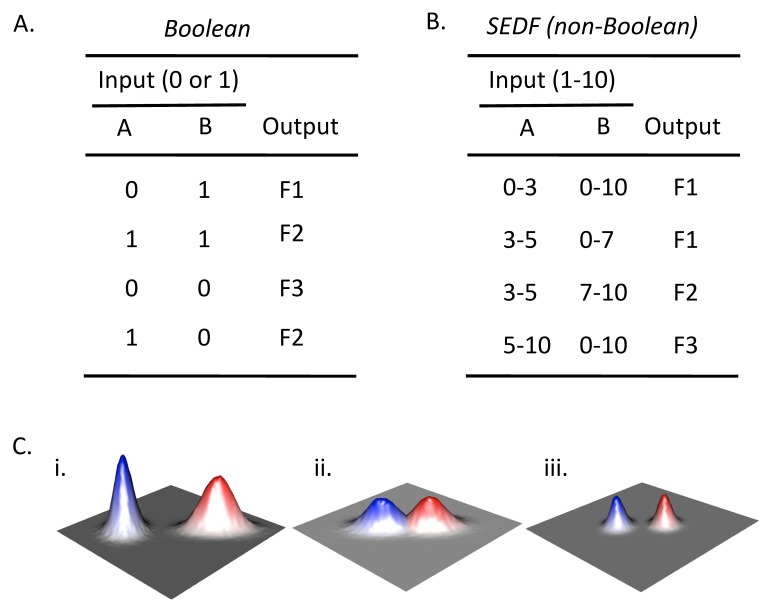
Figure 2. FIGURE 2: Boolean and non-Boolean relationships between input and output.

(A) Boolean truth table that represents the relationship between all combinations of the presence (1) or absence (0) of two possible inputs (A and B) and the occurrence of a given output. With respect to differentiation choices, examples of inputs could be the presence/absence of particular environmental cues or the activation/ inactivation of particular signaling pathways, and examples of outputs would be the occurrence (1) or not (0) of a particular type of differentiation. In an authentic Boolean truth table the response (as well as signal) would be only "1" or "0", but for the example given, three alternative fates (F1-F3) are indicated for conciseness. As a result, this table can be considered a collapsed stack of truth tables, with one truth table for each possible fate.

(B) Example of non-Boolean relationship between input and output. Rather than a given input being present or absent, the amount of input affects the output. In the context of differentiation choices, the amount of input could reflect the concentration of a particular environmental cue or the level of activation of a given signaling pathway. Note that in the contrived example shown, when the amount of input A is constant, output depends on the amount of input B not merely its presence or absence (compare row 2 and 3).

(C) Environmental landscape graphs showing theoretical relationship between the efficiency/probability of cell fate (Z-axis) and two environmental variables (X- and Y-axes). The red and blue peaks represent two different cell fates. (i) In a Boolean landscape, fates are discrete, they never occur in the same environment, also Boolean response peaks are symmetric relative to the axes, so the blue peak is Boolean and the red peak is not. (ii) SEDF model is not Boolean since the two fate response peaks overlap. (iii) Even in the SEDF model, fates can be made discrete by reinforcing small differences in environment by cell-cell signaling.