Figure 1. The emergence of global oscillation due to the introduction of shortcuts to the regular square lattice, as observed in different versions of the rock-paper-scissors game (see legend).

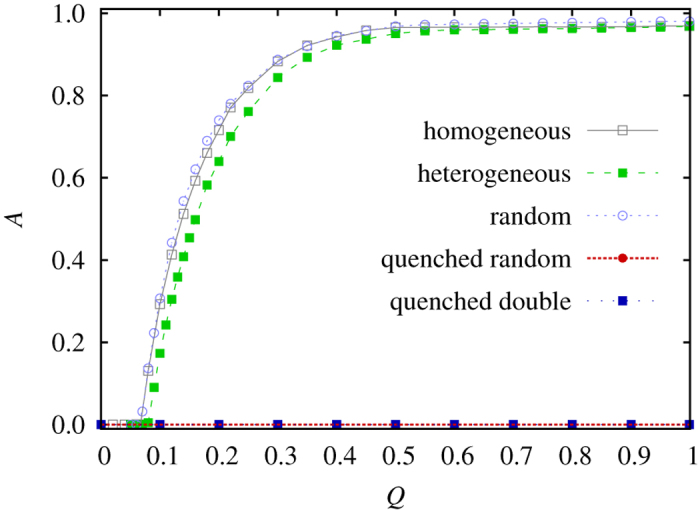
Here Q denotes the fraction of rewired links, while A is the area of the limit cycle in the ternary diagram (see Methods). In the homogeneous case all species-specific invasion rates δ_i are equal to 1, while in the heterogeneous case we use δ₀ = 0.6, δ₁ = 0.8, and δ₂ = 1 throughout the simulation. With random, we denote the case where δ_i are chosen uniformly at random from the unit interval at each particular instance of the game. Lastly, quenched random and quenched double correspond to results obtained with site-specific invasion rates drawn from a uniform distribution and from a discrete double-peaked distribution, respectively. Importantly, site-specific invasion rates are determined randomly only once at the start of the game and are thereafter quenched. It can be observed that species-specific invasion rates fail to block the emergence of global oscillations, with the order parameter A rising almost to l for a sufficiently high fraction of rewired links. Conversely, site-specific invasion rates completely suppress the emergence of global oscillations, and this regardless of the underlying distribution. As it is specified in the Method section, to produce this plot we have used different system sizes to avoid artificial extinction of species at high oscillation.