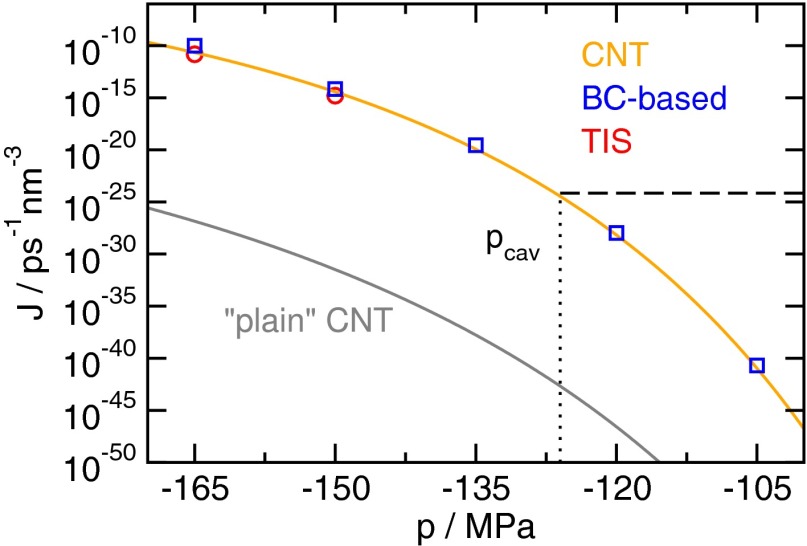
Fig. 4.

Predictions obtained from CNT using microscopic information are in excellent agreement with cavitation rates J from direct simulation. The estimates obtained from simulations by a variant of the Bennett–Chandler method (blue squares) agree well with the transition interface sampling (red circles) reference calculations (Materials and Methods). Predictions of curvature-corrected CNT (orange line) with the correct value of ${\rho }_0$ using the kinetic prefactor shown in Fig. 3 yield excellent agreement with simulation results, whereas plain CNT (gray line) severely underestimates the cavitation rate. For plain CNT, we chose ${\rho }_0=n_l{n}_v$, where $n_l$ and $n_v$ are the number density of the liquid and the vapor, respectively (68). These rate estimates allow for a direct comparison with conflicting experimental predictions on the stability of water under tension by computing the cavitation pressure $p_{\text{cav}}$. Following ref. 22, we define $p_{\text{cav}}$ such that the probability to observe a cavitation event is $P=1/2$ in a system of volume $V=\mathrm{1,000}\hspace{0.17em}\mu {\text{m}}^3$ over an observation time of $\tau =1\hspace{0.17em}\text{s}$. Assuming that the cavitation events are associated with an exponential waiting time, as is typical for activated processes, a rate of $J=\ln 2/\left(V\tau \right)$ (dashed black line) is compatible with this requirement. Its intersection with the CNT prediction gives the cavitation pressure $p_{\text{cav}}\approx -126\hspace{0.17em}\text{MPa}$.