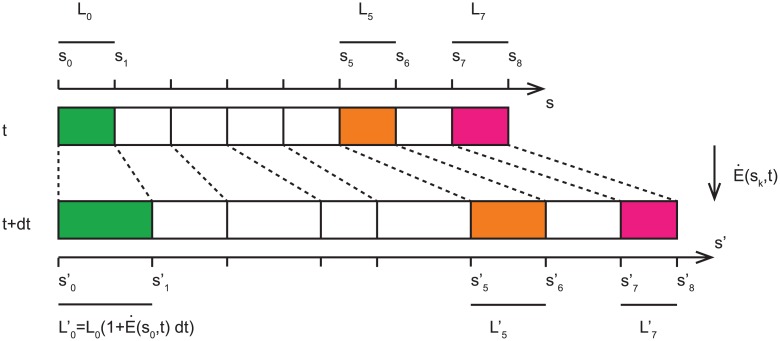
Fig 4. An illustration of the material derivative.

As a simplification, a plant organ can be seen as a succession of elongating elements. Their position along the curvilinear abscissa is given by the lowest position of the element s_i, and its length defined by the position of the subsequent element; L_i = s_i+1 − s_i. For example the 5th element, in orange, starts at point s₅, and its length is defined by L₅ = s₆ − s₅. For simplicity we assume that at time t, all elements have identical length of L_i = L₀, and an elongation rate $\dot{E}(s,t)$ is applied to each element of the organ during a time dt. The elongation of each element is then $L_i^{\prime }=L_i(1+\dot{E}(s,t)dt)$. The difference in length for each element is then $L_i^{\prime }-L_i=L_i\dot{E}(s,t)dt$. In the example of the first element (in green), the position is not modified, i.e. $s_0^{\prime }=s_0$, since this is the basal point which is fixed. However the increase in the element’s length shifts the positions of all other elements, e.g. the next element originally at position s₁ is now at a position $s_1^{\prime }=s_1+L_0\dot{E}(s_0,t)$. The second element is pushed by the elongation of both the basal element at s₀ and the next element at position s₁. Following this argument, the displacement of any element is then given by the sum of the elongations of all previous elements, $s_n^{\prime }-s_n={\sum }_{k=0}^n{L}_0\dot{E}(s_k,t)dt$. The velocity of an element is then given by the displacement of this element $s_n^{\prime }-s_n$ divided by the time interval dt. In the continuous limit, L₀ → ds, this velocity is given by $v(s,t)={\int }_0^{s}d{s}^{\prime }\dot{E}(s^{\prime },t)$. It is important to note that even if locally no elongation occurs, for example for the last element shown in pink with $\dot{E}(s_n,t)=0$, the element is still displaced due to the displacement of previous elements. The change of curvature along the organ can be understood in a similar fashion (see Figure 1 in [14]).