Designs for Phase I trials in ordered groups

Abstract

We propose a new design for dose finding for cytotoxic agents in two ordered groups of patients. By ordered groups, we mean that prior to the study, there is clinical information that would indicate that for a given dose, one group would be more susceptible to toxicities than patients in the other group. The designs are evaluated relative to two previously proposed designs for ordered groups over a range of scenarios generated randomly from a family of dose-toxicity curves.

1. Background

The primary goal of a Phase I trial of a cytotoxic agent in oncology is to estimate the ‘maximum tolerated dose’ (MTD), the highest dose that can be administered with an acceptable level of toxicity. The level of toxicity at a given dose is defined in terms of the proportion of patients who experience a sufficiently severe, protocol-specified adverse event, usually called a ‘dose-limiting toxicity’ (DLT). With cytotoxic agents, it is generally assumed that the greater the dose administered, the greater the probability that a patient will experience a DLT.

In some cases, the phase I trial is designed to include heterogeneous groups of patients, and the goal is to estimate an MTD within each group. Ramanathan et al. [1] stratify patients into ‘none,’ ‘mild,’ ‘moderate,’ or ‘severe’ liver dysfunction at baseline. LoRusso et al. [2] uses a similar classification. Dasari et al. [3] defined groups in terms of type of cancer, while Prados et al. [4] stratify patients by prior therapies. Ura et al. [5] and Kim et al. [6] conducted phase I trials in groups defined by patient genetic characteristics. These examples use different dose-finding designs within groups; Ramanathan et al. [1] use the traditional 3+3 design, while Ura et al. [5] uses the more efficient continual reassessment method [7], but the trials share the common feature that the MTD in each group is determined only from the data obtained within that patient group. Ignoring the group structure can lead to at least 2 problems: reversals and inefficiency. By reversals, we mean that the MTDs in the groups can contradict what is known clinically. For example, a parallel design might recommend a greater dose level as the MTD in the most severely impaired group compared to a less severely impaired group. By inefficiency, we mean that a design that takes into account the known clinical relationship might recommend the correct MTDs in the groups a greater proportion of times.

Several methods have been proposed to address the problem of patient heterogeneity in dose-finding. O’Quigley, Shen and Gamst [8] introduced a two-sample CRM, which allowed for the identification of the appropriate MTD’s for two groups simultaneously. Legedza and Ibrahim [9] proposed a related method, augmenting the dose-toxicity model for a vector of patient characteristics and putting a prior on the coefficient in the dose-toxicity model. Thall, Nguyen, and Estey [10] introduced a Bayesian sequential Phase I/II method that accounts for the interaction between patient characteristics and dose.

In this paper, we propose a design based on the procedure of Hwang and Peddada [11] a method of estimation for parameters subject to a partial order. These estimates were the basis of a method proposed by Conaway, Dunbar and Peddada (CDP) [12] for dose-finding in trials of combinations of agents. Recent comparisons [13] have shown that in combination agent trials, the CDP method has excellent properties and this motivated us to consider the use of these estimates in trials with heterogeneous groups. The design that we propose modifies the CDP method in several ways to account for the fundamental differences in the conduct and the goals of combination agent trials and trials in heterogeneous groups of patients. One important distinction is that the CDP method for combinations targets a single MTD; in a heterogeneous groups study, an MTD estimate is needed for each of the groups. More importantly, studies of combinations of agents or studies of dose and schedule [14, 15, 16] allow the investigator to assign the dose of both agents or the dose and schedule simultaneously to patients. In heterogeneous groups, the group assignment is a characteristic of the patient, and not under the control of the investigator. In addition to proposing two versions of designs using Hwang-Peddada estimates, this paper will evaluate the proposed and existing methods across a broad range of scenarios for the dose-toxicity relationships in the groups, providing more information about the performance of existing methods than has been published previously.

1.1. Methods and applications in ordered groups

In O’Quigley et al. [8], no assumption was made regarding the order of tolerance towards the treatments between the two groups. O’Quigley and Paoletti [17] proposed a two-parameter CRM for ordered groups that utilizes known differences between the groups. Morita [18] presented an application of the CRM that utilized information from Caucasian patients in order to design a phase I dose-finding study for Japanese patients. Ivanova and Wang [19] also incorporate isotonic estimates into designs for ordered groups that take into account both toxicity and efficacy endpoints. Wages, Read and Petroni [20] describe the design of a dose-finding trial that explicitly uses the known ordering in the probabilities associated with ’good’ and ’poor’ prognosis patients. Their design is based on the shift model [21, 22] that generalizes the CRM to two ordered groups.

In this paper, we compare our proposed methods to two generalizations of the CRM. Yuan and Chappell [23] propose a hybrid of the single agent-single group CRM and isotonic regression methods [24]. As in the single agent CRM, the working model and the data within each group are used to estimate the DLT probabilities at each dose for that group. Using the algorithms described by Robertson, Wright and Dykstra [24] for two-way isotonic regression, the resulting DLT probability estimates within each dose level are modified so that there are no reversals, meaning no dose levels where a lower risk group has greater DLT probability estimates than a higher risk group, and preserves the monotonicity of toxicity probabilities within groups.

Another generalization of the CRM to ordered groups is the shift model [21, 22]. To illustrate this method, we assume that DLT probabilities are at least as great in group 2 as in group 1. One way to interpret the notion of at least as much toxicity in group 2 as in group 1 is to say that we anticipate that the MTD in group 2 will be L dose levels lower than in group 1, with L = 0, 1, 2, …, K − 1. Using the simple power model, as in the original CRM, the DLT probability at dose level k in group 1 are equal to ${\psi }_k^{\text{exp}(a)}$. A shift of L = 0 means that the DLT probabilities are the same in the two groups. If L = 1, the probability of a DLT in group 2 at dose level k is equal to ${\psi }_{k+1}^{\text{exp}(a)}$. The method uses the data from all group-dose combinations to estimate the parameter a and the magnitude of the shift L, L = 0, 1, 2, …, K − 1.

2. The proposed design

An example of a dose-finding study in ordered groups is given in [20]. In the actual study, both measures of toxicity and efficacy were considered, and the dose levels under consideration differed between the groups. To motivate our proposed designs, we will use a simplified version of the study in which there are two groups of patients, those with a poor prognosis and those with a good prognosis, toxicity is the only endpoint, and there are 4 doses of radiation in each group. The probability of a DLT at dose j, j = 1, …, 4 in group g, g = 1, 2 is denoted by by π_gj. In Table 1, within each row, the probability of a DLT will increase across columns, π_gj ≤ π_gj′ for j < j′. Within columns, the probability of a DLT is greater for the poor prognosis population than for the good prognosis population, π_1j ≤ π_2j, where g = 1 represents good prognosis and g = 2 represents poor prognosis. The probabilities in Table 1 are a partial order [24] because there are pairs of parameters, π₁₂ and π₂₁ or π₁₄ and π₂₂ for example, for which the ordering is not known prior to the study.

Table 1.

An example of 4 doses in 2 ordered groups. “π” denotes the probability of DLT at each group-dose combination.

		Dose
group	prognosis	8	10	12.5	15
2	poor	π21	π22	π23	π24
1	good	π11	π12	π13	π14

2.1. Pre-trial specifications

Before the trial begins, we choose a set of M guesses at the orderings among the parameters. As described in [25, 26], this set of M orderings need not be all possible simple orders orders consistent with the partial order. In this example, we choose M = 8 possible orders out of a total of 14 possible simple orders. The chosen orders are displayed in Table 2. Ordering 1 is ‘ordered by columns’ and suggests that the group effect is smaller than the increase in the toxicity probability between adjacent doses. Ordering 2 is ‘ordered by rows’ and suggests a large group effect, where the probability of a DLT at the highest dose in the good prognosis group is less than the probability of a DLT at the lowest dose in the poor prognosis group. Orders 3, 7 and 8 are motivated by the shift model, with a shifts of 1, 2 or 3 levels in the MTD. Orders 4 through 6 suggest that the group effect is smaller at lower doses than at higher doses. The orderings used here were suggested by heuristic arguments about how the dose-toxicity curves might differ between two ordered groups. In an actual clinical trial, different orderings might be chosen based on clinical knowledge of the groups and the agent under study.

Table 2.

Chosen orders for 4 doses in 2 ordered groups

Ordering	Guess at unknown orders
1	π11	≤	π21	≤	π12	≤	π22	≤	π13	≤	π23	≤	π14	≤	π24
2	π11	≤	π12	≤	π13	≤	π14	≤	π21	≤	π22	≤	π23	≤	π24
3	π11	≤	π12	≤	π21	≤	π13	≤	π22	≤	π13	≤	π23	≤	π24
4	π11	≤	π12	≤	π13	≤	π21	≤	π14	≤	π22	≤	π23	≤	π24
5	π11	≤	π12	≤	π21	≤	π22	≤	π13	≤	π23	≤	π14	≤	π24
6	π11	≤	π12	≤	π21	≤	π22	≤	π13	≤	π14	≤	π23	≤	π24
7	π11	≤	π12	≤	π13	≤	π21	≤	π22	≤	π23	≤	π14	≤	π24
8	π11	≤	π12	≤	π14	≤	π13	≤	π22	≤	π23	≤	π14	≤	π24

In addition to choosing the orderings prior to the study, we need to decide on the ’possible escalation doses’ for each of the dose-group combinations under study. By definition, the possible escalation doses associated with a specific group-dose pair are the group-dose pairs that can be tried if the specific group-dose pair has been deemed sufficiently safe [25]. In combination agent trials or in dose-finding for multiple schedules, this choice gives the investigator some flexibility in how conservatively or aggressively escalation can occur. In the heterogeneous group case, the choice is simpler; the possible escalation dose for group-dose pair (g, j), j = 1, … J and g = 1, …, G is (g, j + 1) for j < J and (g, J) for j = J.

The final pre-trial specification is a beta prior with parameters (α_gj, β_gj) for the probabilities of a DLT for each group-dose pair. As in [25], we elicit these priors by asking investigators to specify an expected probability of a DLT and a value that they are 95% sure that the probability will not exceed. From these two values, we can solve for the parameters (α_gj, β_gj). These prior values will be used as smoothing parameters in the Hwang-Peddada estimation.

2.2. Stage 1

We propose a two-stage design that uses single patient cohorts until a toxicity is observed and takes into account the ordering between groups [17, 25, 27]. For example, if the first 2 patients are from the poor prognosis group and are given dose levels 1 and 2 respectively, and neither patient experiences a DLT, then if the next patient is from the good prognosis group, that patient can be assigned to dose level 3. In general, in stage 1, a new patient in group g is assigned to one dose level greater than the highest dose observed so far with no DLTs from patients in group g or in any higher risk group. Once a DLT is observed in any patient in any group, stage 2 begins.

2.3. Stage 2

Stage 2 is iterative and will continue until we have observed a pre-chosen number of patients. At any point in the iteration, N_gj patients in group g have received dose level j. Of these, Y_gj patients have experienced a DLT, g = 1, …, G and j = 1, …, J, and the log-likelihood is

$$L_m=\sum _{(g,j)}{Y}_{gj}\text{ ln}({\pi }_{gj})+(N_{gj}-Y_{gj})\text{ ln}(1-{\pi }_{gj})$$ (1)

Using the beta prior, we compute ’smoothed’ observed proportions, ${\hat{\pi }}_{gj}=\frac{Y_{gj}+{\alpha }_{gj}}{N_{gj}+{\alpha }_{gj}+{\beta }_{gj}}$ and compute Hwang-Peddada estimates, denoted ${\hat{\pi }}_{gj}^{HP}(m)$ for each of the m = 1, …, M pre-specified orders, using only those group-dose pairs with N_gj > 0. The method of smoothing the estimates prior to computing isotonic estimates is also found in [14, 25]. The algorithm for computing the Hwang-Peddada estimates is given in the Appendix. For each of the M orders, we evaluate the log-likelihood L_m (2) at the HP estimates under the assumed ordering.

$$L_m({\hat{\pi }}^{HP})=\sum _{(g,j):N_{gj}>0}{Y}_{gj}\text{ ln}({\hat{\pi }}_{gj}^{HP}(m))+(N_{gj}-Y_{gj})\text{ ln}(1-{\hat{\pi }}_{gj}^{HP}(m))$$ (2)

We propose two versions of the design depending on how the sets of estimates from each of the M models are used. The first selects the ordering that yields the largest value for (2) when evaluated at the corresponding Hwang-Peddada estimates. If two or more orders have values equal to the maximum, we choose among these orderings at random. Denoting the chosen order by m*, the current estimated probabilities of toxicity, π̂_gj is equal to ${\hat{\pi }}_{gj}^{HP}(m^{*})$.

The second version uses a weighted average of the Hwang-Peddada estimates from each of the orderings, with the weights proportional to (2) evaluated at the H-P estimates. With the weighted average, the current estimated probability of toxicity are given by (3).

$${\hat{\pi }}_{gj}=\sum _{m=1}^M{w}_m{\hat{\pi }}_{gj}^{HP}(m),\text{ with }{w}_m=\frac{\text{exp}(L_m({\hat{\pi }}^{HP}))}{{\sum }_{m=1}^M\text{exp}(L_m({\hat{\pi }}^{HP}))}$$ (3)

Empirically, we have observed that the properties of the method are greatly improved if the single correct ordering is chosen. In practice, this is unrealistic, and we considered a simple method of adapting the number of orderings to try to capitalize on the improvements that come with selecting the correct ordering. After 5/8 of the patients have been accrued, we choose the 3 orderings with the largest values of (2). The remainder of the trial is done with only those three orderings under consideration.

Once the current estimates have been computed, if the next patient is in group g, the recommended level for this patient is the dose level j*, such that j* = arg min_j(|π̂_gj − θ|). If the estimated probability of a DLT for the suggested dose, π̂_gj*, is less than the target, and there have been no patients as yet allocated to the possible escalation dose (g, j* + 1), then the recommended dose for the next patient is (g, j* + 1). This process continues until a pre-specified number of patients have been accrued. Other measures of the deviation from the target could be used, such as an asymmetric distance that penalizes deviations above the target more than deviations below the target [25]. In our evaluations of the method, however, we will only use the absolute distance loss and set the target equal to 0.20.

3. Comparison of methods

We will evaluate both versions of the proposed method, with the estimated toxicity probabilities chosen from the largest value of L_m evaluated at the corresponding HP estimates and the weighted average method with adapting the number of orderings partway through the trial. The “default” beta priors for the simulations all have mean 0.2, equal to the target toxicity level θ, and an upper limit of 0.70, yielding a beta distribution with α = 0.41 and β = 1.65 for each group-dose pair. For the 2 × 4 case, the 8 orderings listed in Table 2 were used. In the 2 × 6 case, 12 orders were used, and in the 2 × 8 case, 16 orders were hypothesized. For the weighted average method, the number of orderings was reduced to 3 after 20 patients when the total n was equal to 32, at 30 patients when n = 48 and at 40 patients when total n = 64.

The two versions of the method will be compared to the shift model [22], using the skeleton values given in this paper and a pseudo-data prior with mean 0.20 at every level, and with total weight equal to one patient across all doses and groups. A second comparison is the method of Yuan and Chappell [23], choosing a skeleton with the method of Lee and Cheung [28] and with the same pseudo-data prior as for the shift model.

For two ordered groups we varied the number of doses per group (4, 6 and 8) and the trial sample size (32, 48, 64) and evaluated the methods over 1000 scenarios randomly generated from a family of dose-toxicity curves. The 1000 scenarios allowed us to do other investigations of the relative performance of the methods, including a comparison of the methods by the pattern of MTDs and the magnitude of the shift, the difference in the MTD between groups. For each scenario, we ran 500 simulated trials; for any individual scenario, this yields a standard error for estimating the PCS that is no greater than 0.022 percentage points. Averaged over 1000 scenarios, the average PCS values have a standard error that is no greater than 0.007. The supplemental material gives additional simulation results for a selected set of 12 scenarios, chosen by applying K-means clustering to the 1000 scenarios in each of the 4-, 6- and 8-dose cases. In the simulations with specific scenarios, we also varied the proportion of patients in group 1 (0.25, 0.5 and 0.75).

3.1. A family of curves

We generated scenarios at random [29] to create a range of shapes and toxicity probabilities within groups, and preserve the ordering between groups. The basis of the model is the four parameter logistic model for the probability of a DLT, π_gx at dose level x in group g,

$${\pi }_{gx}=1-\frac{1}{1+{\left(\frac{x}{c_g}\right)}^b}$$ (4)

where b was chosen to be constant across groups and c₁, c₂, …, c_G are generated so that c₁ > c₂ > … > c_G. We laid out a grid of possible dose levels, with x taking integer values between 0 and 20, and b generated as U(2, 7). The parameter c₁ was generated as a U(4, 20). The remaining c_g values are generated conditionally, given c_g−1, c_g was generated as U(c_g−1, 20) for g = 2, …, G. Once b and c₁, …, c_G were generated, we computed the dose toxicity probabilities for each group for x = 0 to 20. For the 2-group, 4-dose level scenarios, we selected 4 consecutive x values, x*, x* + 1, x* + 2, x* + 3 such that π_1,x* > 0.01 and π_2,x*+3 < 0.70. For the 2-group, 6 dose level scenarios, we chose 6 consecutive x values such that the lowest dose in the least toxic group had toxicity probability at least 0.01 and the highest dose in the most toxic group had toxicity probability no greater than 0.80. In the 2-group, 8 dose level case, we chose 8 consecutive values of x with toxicity probabilities no greater than 0.90. The supplementary material gives a plot of the first 100 scenarios in each of these cases.

3.2. Analysis of Simulation Results

The two proposed methods and the two existing methods are compared on the basis of 1) the accuracy index (AI) [30], a measure that incorporates the entire distribution of the doses selected to be the MTD selection and 2) the percentage of correct selection (PCS), the percentage of times the method correctly selects the dose with the toxicity probability closest to the target. Within group g, the accuracy index is

$$A{I}_g=1-J\frac{{\sum }_{j=1}^J{\rho }_{j}P(\mathit{\text{selecting dose }}j\mathit{\text{ in group }}g)}{{\sum }_{j=1}^J{\rho }_j}$$ (5)

where ρ_j is a measure of the deviation of the true toxicity probability at dose j in group g, π_gj from the target θ. Cheung (2011) gives several choices for ρ_j, including an absolute deviation, ρ_j = |π_gj − θ|. The Accuracy Index has a maximum value of 1, occurring when the design always recommends the correct MTD.

Both the AI and the PCS were computed separately for each group; Table 3 shows the AI and PCS averaged over both groups. In this table, ‘HP-L’ and ‘HP-W’ are the proposed methods that use either the estimated probabilities from the ordering with the greatest likelihood when evaluated at the Hwang-Peddada estimates or from a weighted average of Hwang-Peddada estimates. The columns labeled ‘YC’ and ‘OI’ are results from the isotonic version of Yuan and Chappell and the shift model of O’Quigley and Iasonos methods. In some of the scenarios generated at random, the toxicity probabilities associated with the doses did not “bracket” the target probability of 0.20, meaning that either the lowest toxicity probability in a group exceeded the target, or the highest toxicity probability was less than the target. Comparing the performance of the methods in these cases tends to dampen the differences between the methods, and Table 3 displays results for all 1000 scenarios as well as for the subset of scenarios where the toxicity probabilities contain the target.

Table 3.

Accuracy Indices and Percent Correct Selection

		Accuracy Index				PCS
	N	HP-L	HP-W	YC	OI	HP-L	HP-W	YC	OI
2×4	32	0.464	0.468	0.426	0.442	0.600	0.599	0.581	0.599
All scenarios	48	0.497	0.503	0.475	0.493	0.635	0.638	0.628	0.652
(1000)	64	0.510	0.525	0.503	0.521	0.656	0.661	0.659	0.683
2×6	32	0.553	0.550	0.530	0.539	0.481	0.480	0.472	0.482
All scenarios	48	0.600	0.605	0.589	0.602	0.527	0.533	0.530	0.542
(1000)	64	0.626	0.635	0.629	0.639	0.556	0.566	0.569	0.585
2×8	32	0.550	0.542	0.592	0.585	0.363	0.359	0.409	0.395
All scenarios	48	0.601	0.601	0.645	0.642	0.407	0.410	0.467	0.457
(1000)	64	0.628	0.631	0.677	0.675	0.436	0.442	0.508	0.502
2×4	32	0.458	0.467	0.411	0.418	0.576	0.578	0.544	0.551
Bracket	48	0.491	0.500	0.463	0.476	0.611	0.617	0.594	0.608
(708)	64	0.509	0.523	0.493	0.508	0.633	0.640	0.626	0.640
2×6	32	0.549	0.546	0.524	0.533	0.471	0.472	0.457	0.466
Bracket	48	0.595	0.602	0.582	0.596	0.517	0.526	0.515	0.527
(904)	64	0.622	0.633	0.619	0.633	0.546	0.559	0.557	0.572
2×8	32	0.565	0.555	0.589	0.580	0.363	0.359	0.409	0.395
Bracket	48	0.601	0.601	0.645	0.642	0.407	0.410	0.467	0.457
(933)	64	0.628	0.628	0.677	0.675	0.436	0.442	0.508	0.502

Some general recommendations can be given by comparing the methods across different numbers of doses. For the accuracy index in all 1000 scenarios, in the 2 × 4 and the 2 × 6 cases, one of the two proposed methods, HP-W or HP-L has the largest AI for sample sizes n = 32 and n = 48. When n = 64 in the 2 × 4 and the 2 × 6 cases, the AI values for the HP-W and the OI methods differ by only 0.004. For the accuracy index in the 2 × 8 case for all 1000 scenarios, the YC method has the greatest average accuracy index across the 3 sample sizes considered, although the differences between the YC and OI methods are small. In comparing the PCS across all 1000 scenarios, the OI method has the largest values for the both the 2 × 4 and the 2 × 6 cases. For the 2 × 8 case, the YC method has the greatest average PCS.

In the ’bracket’ scenarios, in both the 2 × 4 and the 2 × 6 cases, one of the two proposed methods, HP-L or HP-W, has the highest average accuracy index across the n = 32 and n = 48 sample sizes. For n = 64, the HP-W method has the highest average accuracy index in the 2 × 4 case, but the HP-W and OI methods have the same average accuracy (0.633) for n = 64 in the 2 × 6 case. In the 2 × 8 case, the YC method has the greatest average accuracy index, although these averages are only slightly greater than for the OI method. For the PCS in the ’bracket’ scenarios, in the 2 × 4 case, and the samples sizes n = 32 and n = 48, the HP-W has the greatest average PCS. For the 2 × 4 case with n = 64, the HP-W and OI methods have the same average PCS (0.640). In the 2 × 6 case, all the average PCS values are similar, but with the HP-W or OI generally having the greatest average PCS. In the 2 × 8 case, the YC method has the greatest average PCS for all three sample sizes, but the differences between YC and OI are small.

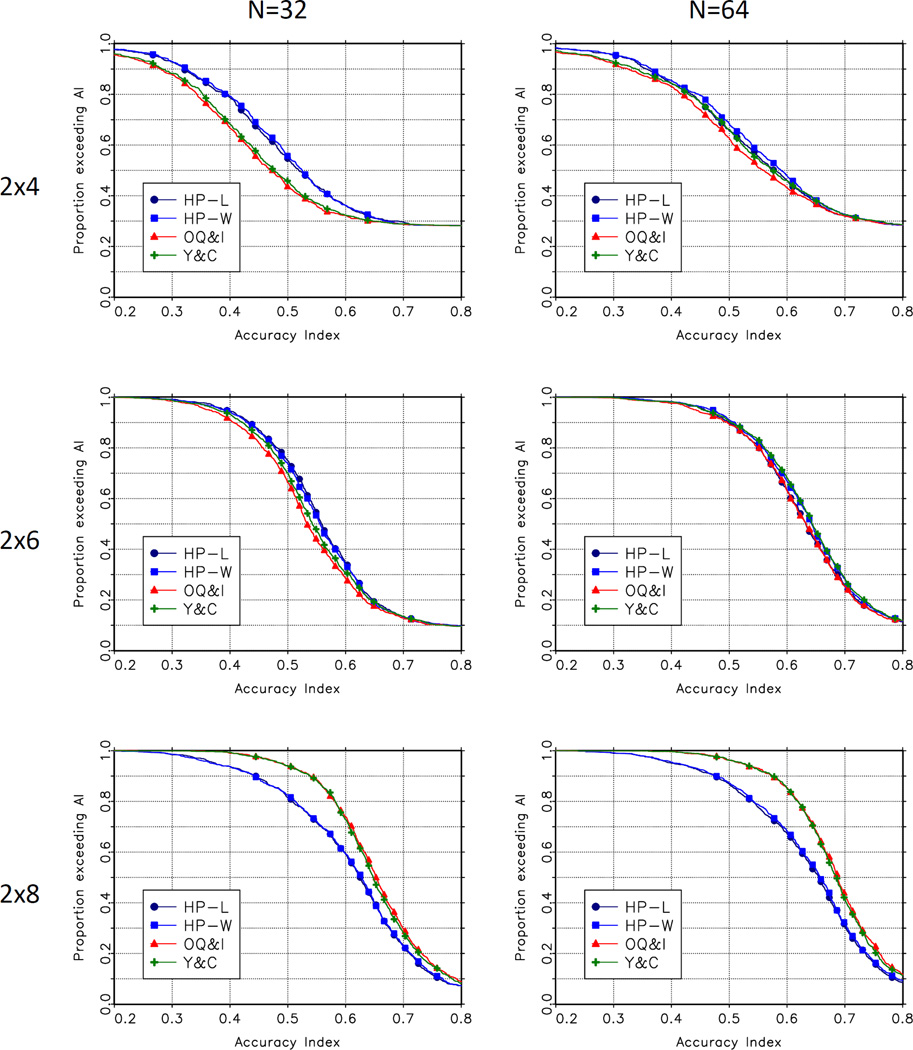
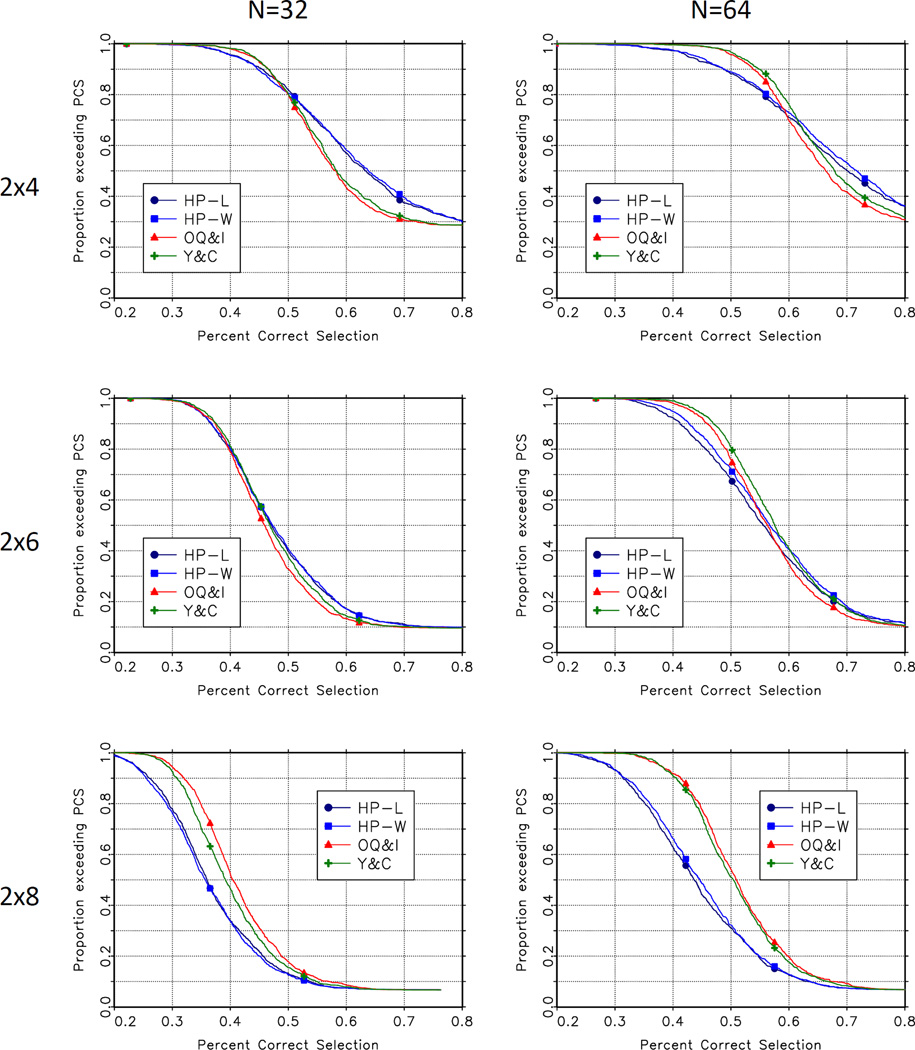
Figure 1 and figure 2 present a more detailed comparison of the performance of the methods. These figures show the empirical survival function for the accuracy index and the percent correct selection for each of the methods, for n = 32 and n = 64 across the 1000 scenarios. The top left panel in figures 1 and 2 show the degree to which the proposed methods dominate the O’Quigley and Iasonos and Yuan and Chappell methods in the 2 × 4 case. The lower right panel in these figures shows the degree to which these CRM-based methods dominate the Hwang-Peddada based methods in the 2 × 8 case.

Figure 1.

Empirical Distributions of Accuracy Index

Figure 2.

Empirical Distributions of Percent Correct Selection

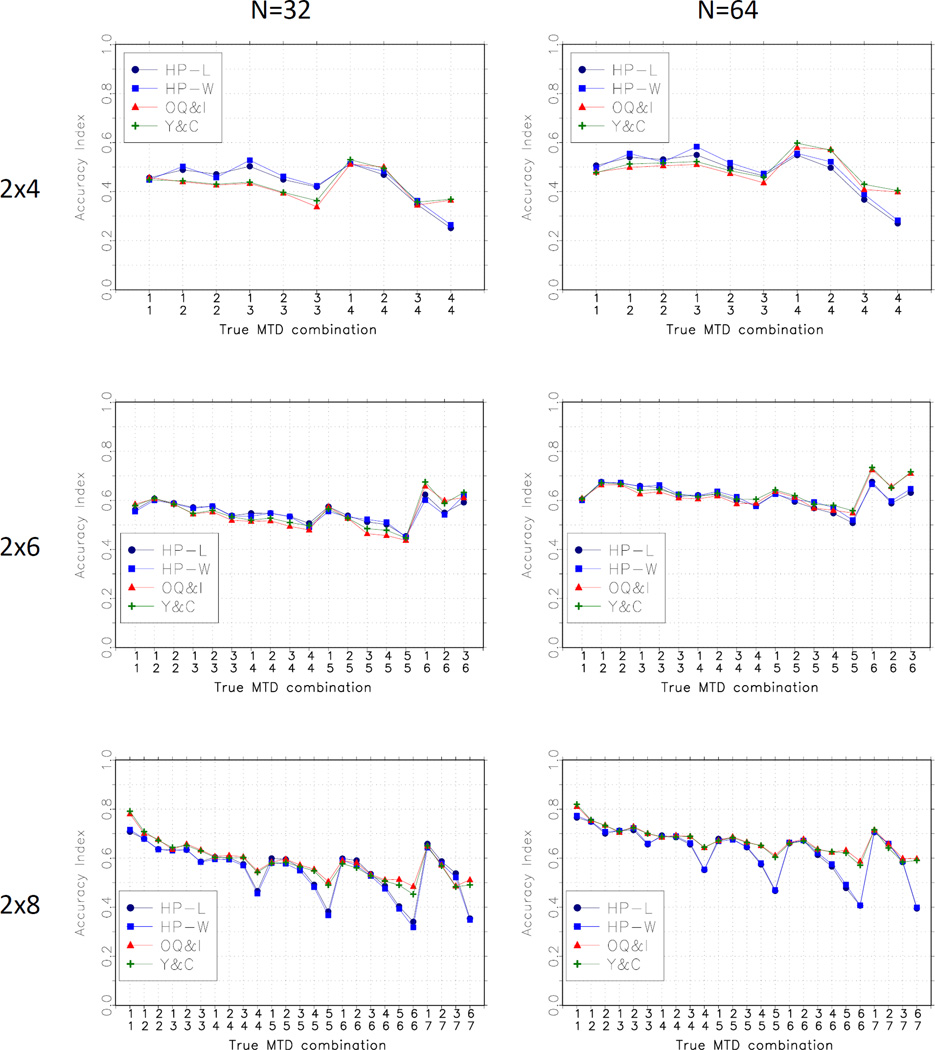
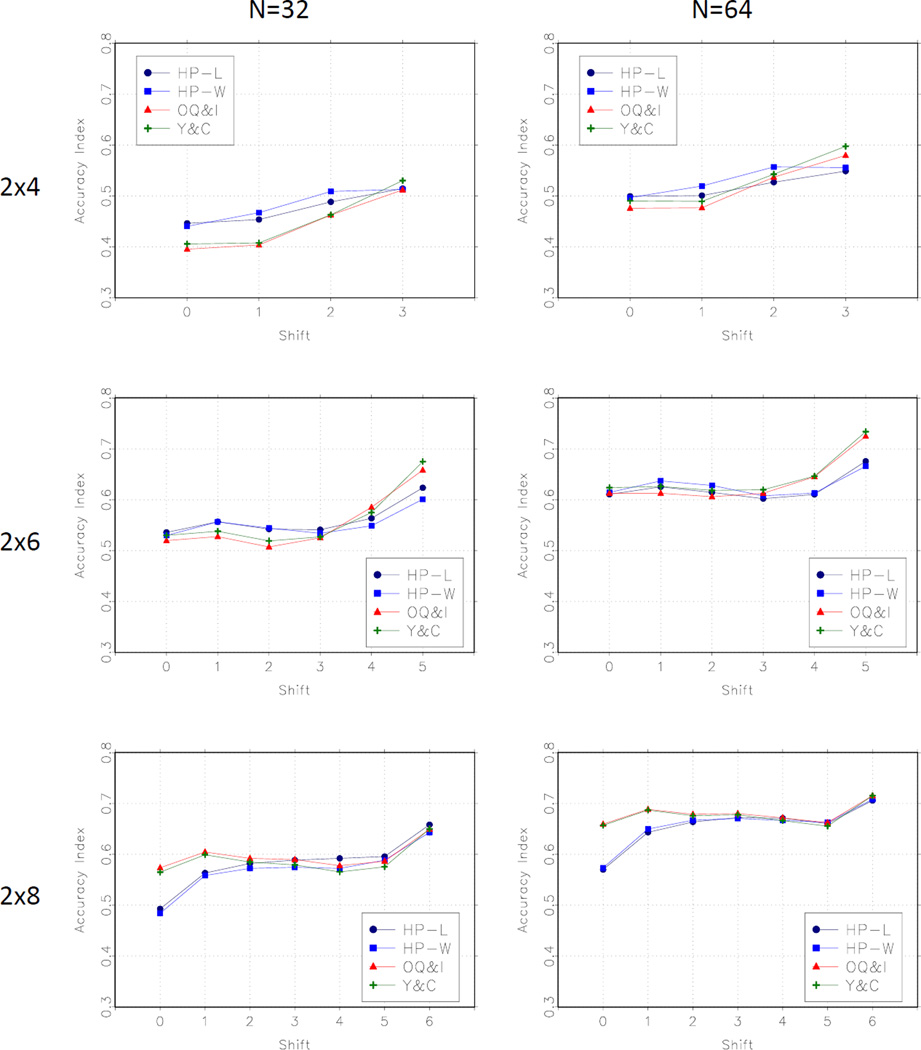
We compared the methods by the configuration of the true MTD, and by the magnitude of the shift between the level of the MTD in the two groups. Figure 3 shows average accuracy index over the bracketing scenarios by the true MTD configuration. This panel suggests that the proposed methods (HP-L and HP-W) perform well when the true MTDs are in the middle of the dose range, and not as well as the Y-C and O-I methods when the MTD is at the highest level in each group. Figure 4 shows the average accuracy index by the degree of the shift. In the 2 × 4 and the 2 × 6 cases, the HP-L and HP-W methods perform best for smaller shifts and relatively less well for larger shifts. The opposite is true in the 2 × 8 case for which the HP-L and HP-W methods do worse for smaller shifts.

Figure 3.

Average Accuracy Index by MTD configuration

Figure 4.

Average Accuracy Index by shift

4. Non-rectangular group-dose studies

In the actual study in [20], the dose levels of interest were not the same in the two groups. Table 4 shows the dose levels under consideration in this study with cells not under consideration colored in gray. Having different dose levels in different groups is not uncommon in studies done in heterogeneous groups. In fact, a ‘non-rectangular’ structure is found in both of the cited studies [1, 2] that we used to motivate the problem of dose finding in ordered groups.

Table 4.

Different doses in 2 groups

	Dose
prognosis	8	10	12.5	15
poor	π21	π22	π23
good		π12	π13	π14

The proposed methods based on Hwang-Peddada estimation require no modification to accommodate these cases. To assess how the properties of these methods are affected by having different dose levels in each group, we simulated trials under the 1000 scenarios summarized in Table 3. We eliminated the group-dose pairs (1, 1) and (2, 4) from each scenario and from the orderings in Table 2. The population proportion in each group was set at 50%, and we assessed sample sizes of 24, 36 and 48. The lower sample size, 24, was included because of the reduced number group-dose combinations under consideration. For the sake of having a method for comparison, we applied the Yuan and Chappell method without any modification to the same set of scenarios. Table 5 displays the results for both the accuracy index and the PCS. As in Table 3, we present results for all 1000 scenarios, and separately for the randomly generated subset of 501 scenarios where the target toxicity probability is within the set of toxicity probabilities in each group. For the scenarios that contain the target, the proposed HP − L and HP −W methods have a greater average accuracy index and percent correct selection than the Yuan and Chappell method for sample sizes of 24, 36 and 48. These methods achieve the same average accuracy index in 24 patients as the Yuan and Chappell method achieves in 36 patients, and nearly the same accuracy in 36 patients as the Yuan and Chappell method achieves in 48 patients.

Table 5.

Comparison of methods for a 2 × 4 nonrectangular case

	Accuracy Index			PCS
N	HP-L	HP-W	YC	HP-L	HP-W	YC
24	0.334	0.329	0.308	0.606	0.595	0.597
32	0.364	0.361	0.357	0.643	0.638	0.641
48	0.383	0.386	0.396	0.661	0.663	0.677
24 (bracket)	0.308	0.307	0.249	0.560	0.557	0.516
32 (bracket)	0.351	0.357	0.309	0.594	0.600	0.565
48 (bracket)	0.372	0.385	0.352	0.614	0.618	0.604

5. Discussion

Our evaluation of two new methods and two existing methods over a range of scenarios suggests that for studies with a smaller number of dose levels, the proposed methods have better performance than the existing methods. In studies with a larger number of doses, the existing methods are preferred. Further research is also needed into methods for choosing and adapting orderings in the proposed methods to assess whether the advantages seen with 4 dose levels can be extended to studies with a greater number of doses. The Yuan and Chappell method was originally proposed for more than 2 groups and we are in the process of extending our proposed methods, and the shift model, to 3 or more ordered groups.

Appendix

Hwang-Peddada estimation

Hwang and Peddada [11] proposed a general method of estimation of parameters subject to a partial order. In a partial order, there are pairs of parameters for which the ordering of the parameters is known, but also pairs for which the ordering is not known. Before describing the design based on these estimates, we will briefly describe Hwang-Peddada estimation for binary variables subject to a partial orders, using the example in Table 1.

Hwang-Peddada estimation depends on a distinction between “nodal” and “non-nodal” parameters. Nodal parameters are those whose ordering with all the other parameters is is known. For example, π₁₁ and π₂₄ are nodal parameters, since π₁₁ is known to be less than, and π₂₄ is known to be greater than, any of the other parameters. The remaining parameters are non-nodal; for each parameter, there is at least one other parameter for which the ordering is unknown; for example, the ordering between π₁₂ and π₂₁ is unknown. Estimation of the nodal parameters proceeds by guessing at the unknown orders among the parameters, making sure that the guess preserves the known orderings. For example, a possible guess at the ordering is given in (6)

$${\pi }_{11}\le {\pi }_{21}\le {\pi }_{12}\le {\pi }_{22}\le {\pi }_{13}\le {\pi }_{23}\le {\pi }_{14}\le {\pi }_{24}$$ (6)

This preserves the monotonicity within rows and within columns, and could be interpreted as a guess that the difference in the probability of a DLT between groups is less than the difference in the probability of a DLT due to changes in dose within a group. Once the guess is made, the parameters follow a ”simple order” and the estimates of the nodal parameters can be obtained with any one of several standard methods in order restricted inference, such as the ’pool adjacent violators algorithm’ (PAVA) or the minimum lower sets algorithm [24]. At this stage, we retain the estimates of the nodal parameters and discard the estimates of the non-nodal parameters. In the example, at this point, we have estimates π̂₁₁ and π̂₂₂. To estimate each of the non-nodal parameters, we delete the smallest number of parameters from the set that will make the given parameter nodal. For example, to estimate π₁₂, if we were to remove π₂₁, then π₁₂ would be a nodal parameter. The parameter π₁₂ could be estimated using a modification of the PAVA algorithm for the simple order 7 determined by our guess at the unknown orderings, with π₂₁ removed, and π₁₁ and π₂₄ fixed at their previously estimated values.

$${\hat{\pi }}_{11}\le {\pi }_{12}\le {\pi }_{22}\le {\pi }_{13}\le {\pi }_{23}\le {\pi }_{14}\le {\hat{\pi }}_{24}$$ (7)

Estimation proceeds until all the nodal and non-nodal parameters have been estimated. Further details on computational aspects, other examples and the statistical properties of Hwang-Peddada estimates are given in [11].