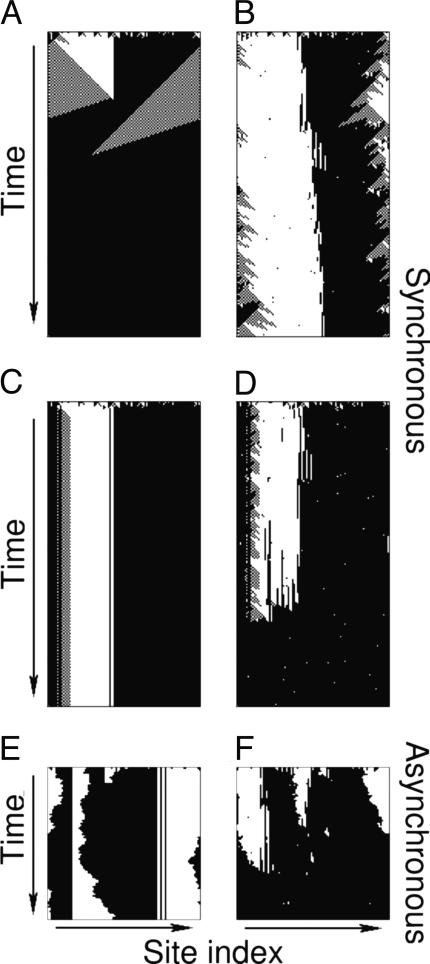
Fig. 1.

Effect of noise intensity η and rewiring probability p on the time evolution of a system of CA operating according to the GKL rule (17). We consider systems starting from random configurations that are allowed to evolve for 2N time steps, where N = 99 is the number of units in the system. (A) p = 0 and η = 0. In this case, which corresponds to the classic GKL rule, the system shows the sophisticated dynamics studied in ref. 13 with the boundaries of the domains traveling in opposite directions. The domains quickly merge, and the units find a consensus state. (B) p = 0 and η = 0.05. In this case, the noise destabilizes the dynamics of the domains, and the system does not converge to a consensus within 2N time steps. (C) p = 0.05 and η = 0. Without the regularity of the one-dimensional lattice, the GKL rule is unable to process local information properly. As a result, the system typically reaches a stable configuration but does not converge to a consensus. (D) p = 0.05 and η = 0.05. It is surprising that when both noise and rewiring are present, the system is able again to converge to consensus. (E) With asynchronous updating, the GKL rule is not capable of coordinating the domain dynamics, and the system does not reach the consensus when p = 0 and η = 0. (F) p = 0.05 and η = 0.05. For asynchronous update, a system with both noise and rewiring still converges to a consensus. As we will see later, in the presence of noise and rewiring, the GKL rule operates analogously to the majority rule.