Fig. 3.

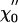Responsiveness to sinusoidal stimulation. (A) The real part of the linear response function χ₀ displays a peak near the bundle's frequency of spontaneous oscillation, and is positive everywhere. (B) The imaginary part changes sign at a frequency near that of the bundle's spontaneous oscillation. The external sinusoidal force had an amplitude of 2 pN. From the fit (red lines) of the response function χ₀ by Eq. 10, we found α ≃ 0, K = 74 μN·m^-1, Λ = 4.3 μN·s·m^-1, and ν₀ = 2πω₀ = 8.6 Hz, which is in quantitative agreement with the response function measured for an oscillatory hair bundle (5). (C) The sensitivity |χ| displays a nonlinear compression in a regime of intermediate forces 3 - 30 pN when the magnitude of an external sinusoidal force is increased at the frequency of the spontaneous oscillations. This nonlinearity is consistent with a power law with an exponent of -2/3 (red line). A fit to the relation yielded the nonlinear coefficient |B| ≃ 1.2 10¹²N·m^-3. For stimuli smaller than ≃ 1 pN, the sensitivity saturates at 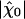≃ 8.5 km·N^-1 (green line). For stimuli larger than ≃ 300 pN, the sensitivity approaches a constant, minimal value of 1 km·N^-1 (green line). The parameters used in the simulation are the same as in Fig. 2.