Design of Sequentially Randomized Trials for Testing Adaptive Treatment Strategies

Abstract

An adaptive treatment strategy (ATS) is an outcome-guided algorithm that allows personalized treatment of complex diseases based on patients’ disease status and treatment history. Conditions such as AIDS, depression, and cancer usually require several stages of treatment due to the chronic, multifactorial nature of illness progression and management. Sequential multiple assignment randomized (SMAR) designs permit simultaneous inference about multiple ATSs, where patients are sequentially randomized to treatments at different stages depending upon response status. The purpose of the article is to develop a sample size formula to ensure adequate power for comparing two or more ATSs. Based on a Wald-type statistic for comparing multiple ATSs with a continuous endpoint, we develop a sample size formula and test it through simulation studies. We show via simulation that the proposed sample size formula maintains the nominal power. The proposed sample size formula is not applicable to designs with time-to-event endpoints but the formula will be useful for practitioners while designing SMAR trials to compare adaptive treatment strategies.

1. Introduction

An adaptive treatment strategy (ATS) is an outcome-guided algorithm that allows personalized treatment [1] of complex diseases based on disease status (response, recurrence, remission, relapse) and intermediate treatment history. Complex diseases such as AIDS, depression, and cancer usually involve several stages of treatment due to dynamic disease progression. For instance, a patient with depression may benefit if she initiates treatment with citalopram (CIT). Depending on response, she may remain on CIT or switch to or add another medication or psychosocial treatment during the next phase of treatment [2]. In principle, a clinician monitors a depressed patient and decides on interventions at different time points based on the patient’s clinical status. Availability of multiple treatment options at each stage of treatment, various possibilities for the duration of each stage, and various responses that can be achieved through different stages of therapy could lead to a multitude of adaptive treatment strategies. Examples of treatment strategies for a patient with moderate depression include [2]:

1. Treat with CIT for 6–8 weeks; if response is not achieved with CIT, augment with cognitive behavioral therapy (CBT) for 8 weeks, otherwise continue with CIT for another 8 weeks.

2. Treat with CIT for 6–8 weeks; if response is not achieved with CIT, switch to CBT for 8 weeks, otherwise switch to BUS (buspirone) for another 8 weeks.

3. Treat with CIT for 6–8 weeks; if response is not achieved with CIT, switch to CBT for 8 weeks, otherwise switch to BUP-SR (bupropion sustained release) for another 8 weeks.

4. Treat with CIT for 6–8 weeks; if response is not achieved with CIT, switch to SERT (sertraline) for 8 weeks, otherwise switch to CBT for another 8 weeks.

ATSs are often compared via sequential multiple assignment randomized (SMAR) designs [3, 4, 5]. Even though SMAR trials are useful for comparing ATSs because different ATSs can be tested from the same experimental design and the procedure for inference about ATSs from data arising from such trials are well-established, the design issues (e.g. sample size and power) have not been adequately addressed. This may be due to the challenges posed by the adaptive and sequential nature of SMAR designs. Nevertheless, a few articles have alluded to the development of sample size formula for SMAR designs.

Murphy [5] provides a sample size formula to test the equality of two strategies that do not share same initial sets of treatments, making data from two groups of patients following these strategies statistically independent. Feng and Wahed [6] also constructed a sample size formula for survival outcomes. However, their formula was developed for censored survival times to test equality of point-wise survival probabilities under two ATSs that have the same initial, but different second stage treatments. They also proposed another formula based on weighted log-rank test for the equality of survival curves under two strategies that share different initial treatments [7]. Recently, Li and Murphy [8] presented a sample size formula for survival data to relax the assumptions set forth by Feng and Wahed [6, 7]. Oetting et al. [9] establishes four sample size formulas, of which only two are relevant to adaptive treatment strategies. One of the formulas (referred to as #3 in their chapter) deals with a hypothesis testing the equality of a pair of strategy means. The other relevant formula (referred to as #4 in their chapter) is developed with the goal of finding the best strategy (as opposed to hypothesis testing comparing multiple strategies). Dawson and Lavori [10] also devised a sample size formula for the nested structure of successive SMAR randomizations when the outcome is continuous. They extended the sample size for the usual t-test to be applicable to SMAR trials. Using a semi-parametric approach, their formula includes stage-specific variance inflation factor (VIF) and marginal outcome variance ${\sigma }_Y^2$. Due to the presence of between-strategy covariance, one cannot make inference for a pair of strategy means that share the same initial treatments by just pooling the VIF’s and marginal outcome variances across the stages. As a remedy, Dawson and Lavori [11] proposed a conservative approach to adjust the sample size formula using the VIF. The caveat with their approach is its difficulty of application. It involves cumbersome computation of all stage-specific VIFs, ${\sigma }_Y^2$ and coefficient of determination by regressing the final outcome on previous states. A more recent simulation work by Ko and Wahed [13] looked into the power for detecting differences between multiple strategy means for arbitrary sample sizes for a two-stage SMAR design.

Most of the works related to sample sizes in SMAR trials are either confined to two-strategy comparison [3, 7] or require assumptions about population parameters that are difficult to ascertain (e.g. VIF’s and stage-specific variances) in multi-strategy comparison settings. The goal of this paper is to provide sample size formulas for a variety of SMAR designs in order to test specific alternative hypotheses related to continuous outcomes. Specifically, we consider three SMAR designs that are being used in various disease areas. The parameters needed to be specified in advance correspond to well-defined subgroups in the patient population and hence are relatively simple to specify. We verify the sample size formulas through simulation experiments.

2. Set-up

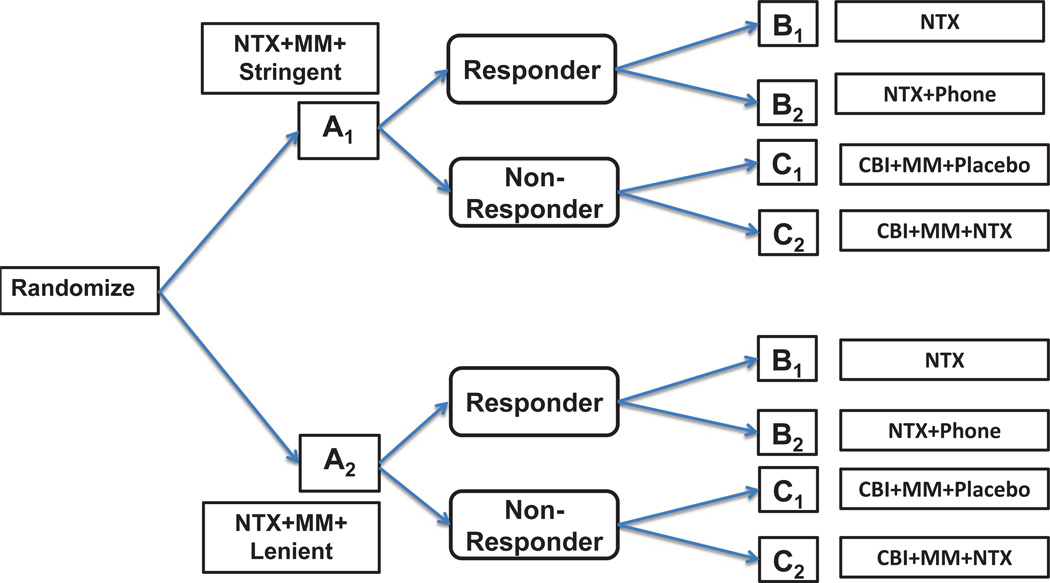
We consider three two-stage SMAR designs. Figures 1, 2 and 3 display the three SMAR designs. In the first design, n subjects are to be randomized to two initial treatments A_j, j = 1, 2. Then second stage treatments, B_k, k = 1, 2, are to be administered randomly if they responded to initial treatments, or else they are randomized to C_l, l = 1, 2.

Figure 1.

Design 1. At entry, patients are randomized to initial treatments A₁ and A₂. If a patient responds to the initial treatment she is randomized to either B₁ or B₂, otherwise the patient is randomized to either C₁ or C₂.

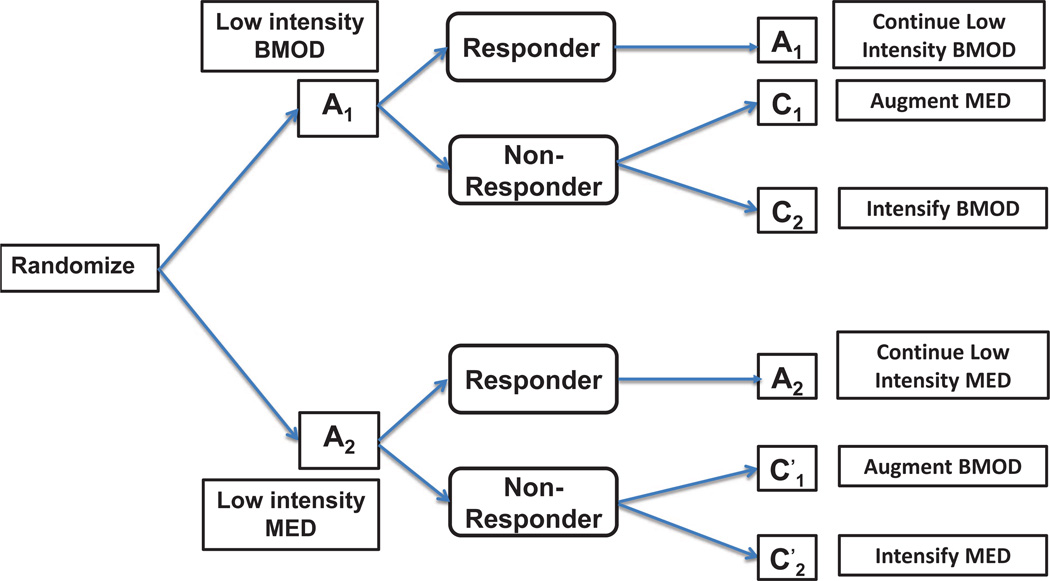
Figure 2.

Design 2. At entry, patients are randomized to initial treatments A₁ and A₂. If a patient responds to the initial treatment she stays on the same initial treatment, otherwise the patient is re-randomized to subsequent treatments: C₁ or C₂ if she does not respond to A₁; $C_1^{\prime }$ or $C_2^{\prime }$ if she does not respond to A₂.

Figure 3.

Design 3. At entry, patients are randomized to initial treatments A₁, A₂ and A₃. If a patient responds to the initial treatment she stays on the same initial treatment, otherwise the patient is re-randomized to subsequent treatments: A₂ or A₃ if she does not respond to A₁; A₁ or A₃ if she does not respond to A₂; A₁ or A₂ if she does not respond to A₃.

We use the Lei et al. [1] design for alcohol-dependence interventions as an example to explain the first design (Figure 1). All patients are provided with “NTX+MM” as their initial treatment (NTX = naltrexone, MM = medical management). Then patients are randomized to two groups based on how the intermediate response to “NTX+MM” would be ascertained. In one group, referred to as A₁, the response criteria would be stringent (5+ days of heavy drinking), whereas in the other group, referred here forth as A₂, the criterion would be lenient (2+ days of heavy drinking). Following eight weeks of treatment, participants are randomized to the second line treatments depending on their non-response status. Non-responders were re-randomized to either “NTX” (B₁) or “NTX+Phone” (B₂), otherwise, they were re-randomized to two maintenance treatments: “CBI+MM+Placebo” (C₁) or “CBI+MM+NTX” (C₂), where CBI = combined behavioral intervention. At the end of the study, the primary outcome (defined as “percent of heavy drinking days” over the last two months of the study) was obtained.

The above design allows inference related to eight possible ATSs, namely A_jB_kC_l, j, k, l = 1, 2, where A_jB_kC_l stands for “Treat with A_j followed by B_k if they respond, or by C_l if not”. For example, one might want to test the equality of all strategy means H₀ : μ₁₁₁ = μ₁₁₂ = μ₁₂₁ = μ₁₂₂ = μ₂₁₁ = μ₂₁₂ = μ₂₂₁ = μ₂₂₂, where μ_ijk is the mean response under strategy A_jB_kC_l, j, k, l = 1, 2 against the alternative of at least one pair being different. Testing equality of any combination of treatment strategies (e.g. pairwise comparisons) may also be of interest. In the sequel we consider the sample sizes required to test varieties of treatment strategy comparisons with adequate statistical power.

The second design was used by Pelham et al. [14] for an Attention Deficit Hyperactivity Disorder (ADHD) clinical trial (Figure 2). This trial involved treating children with ADHD with behavioral and pharmacological interventions during stage 1. In the first stage participants were randomized to low intensity “psychostimulant drug (low intensity MED)” (A₁) or low intensity “behavioral modification (low intensity BMOD)” (A₂). Behavioral modification consists of school-based, weekend and at-home activity sessions. A child’s response to the first line treatment is assessed using Impairment Rating Scale (IRS) and an individualized list of target behaviors (ITB). IRS is a comprehensive measure of improvement in social performance while ITB is a child-specific monitor of social performance. IRS and ITB are “tailoring” variables that determine response status and randomization to the second stage treatments. Based on these tailoring variables, participants who responded to first-stage treatment remained on the same treatment whereas non-responders were re-randomized. Children who did not respond to low intensity BMOD (A₁) were re-randomized to either intensified BMOD (C₁) or BMOD augmented with MED (C₂). Those children who did not respond to low intensity MED (A₂) were re-randomized to either intensified MED $(C_1^{\prime })$ or MED augmented with BMOD $(C_2^{\prime })$.

Thus, if a patient responds to A₁ then she stays on A₁ but is randomized to C₁ or C₂ otherwise. Similarly, if a patient responds to A₂ then she stays on A₂, otherwise she is randomized to either $C_1^{\prime }$ or $C_2^{\prime }$. Formally, there are 4 possible treatment strategies for this design; namely, A₁C₁, A₁C₂, $A_2{C}_1^{\prime }$, or $A_2{C}_2^{\prime }$, where, for example, A₁C₁ stands for “treat with A₁, if do not respond to A₁, treat with C₁. It might be of interest to test equality of all 4 strategy means, H₀ : μ₁₁ = μ₁₂ = μ₂₁ = μ₂₂, where μ_1l and μ_2l are the mean responses for the population following strategy A₁C_l and $A_2{C}_l^{\prime }$ respectively for l = 1, 2.

The third design considered is described in Thall et al. [16] (Figure 3). Patients received one of three initial treatments A₁, A₂ and A₃ during the first randomization. If a patient initially assigned to A₁ responded, she would remain on A₁ during the second stage; otherwise she would be randomized to A₂ or A₃. Similarly, if a patient responds to initial treatment A₂ then he/she would continue A₂ in the second stage; otherwise would be randomized to A₁ or A₃. Similarly, patients not responding to A₃ would be re-randomized to A₁ or A₂ in the second stage. Six possible strategies for Design 3 are A_jA_l, j, l = 1, 2, 3; j ≠ l, where A_jA_l is defined as “treat with A_j followed by A_l if he/she is a non-responder”. The null hypothesis of equality of strategy means is, H₀ : μ₁₂ = μ₁₃ = μ₂₁ = μ₂₃ = μ₃₁ = μ₃₂, where μ_jl is the mean response under strategy A_jA_l, l ≠ j; j, l = 1, 2, 3.

For all the three designs, we develop a sample size formula to detect meaningful differences between strategy means. The derivation and discussion of the sample size and variance formulas in Section 3 is based on Design 1. The formulas apply to Designs 2 and 3 directly with only slight adjustment as outlined later in Section 4.

3. Comparing Multiple Treatment Strategies

The goal of this paper is to design a sample size formula for a test that detects differences in strategy means from SMAR designs with a continuous endpoint. In order to achieve this goal, let us introduce the following notation. Let R_j be the counterfactual response indicator for an individual who responded to A_j, j = 1, 2; Y (A_jB_k) is the counterfactual outcome of an individual had he/she received A_j, responded, then took B_k; similarly, Y (A_jC_l) is the counterfactual outcome of an individual had he/she received A_j, did not respond, then took C_l. Based on these three counterfactual outcomes, consider Y (A_jB_kC_l) as the outcome under strategy A_jB_kC_l, which can be written as

$$Y(A_j{B}_k{C}_l)=R_{j}Y(A_j{B}_k)+(1-R_j)Y(A_j{C}_l),j,k,l=1,2.$$ (1)

To clarify the distinction between the observed and unobserved quantities, for example, for a patient who received A₁, responded, and received B₁, {R₂, Y (A₁B₂), Y (A₂B₁), Y (A₂B₂)} are all unobservable. What is observed here is only Y (A₁B₁) (see consistency assumption below). As described in Section 2, we are interested in estimating μ_jkl = E{Y (A_jB_kC_l)}. Conditioning on R_j, μ_jkl can be expressed as

$${\mu }_{jkl}={\pi }_j{\mu }_{A_j{B}_k}+(1-{\pi }_j){\mu }_{A_j{C}_l},$$ (2)

where π_j is the response rate for the first stage treatment A_j; μ_AjBk = E{Y (A_jB_k)} is the sub-group mean of the population receiving A_j followed by B_k, μ_AjCl = E{Y (A_jC_l)} is sub-group mean of the population receiving A_j followed by C_l. Our development of the sample size formula is based on Wald-type test statistics. Thus, an estimator of the strategy means and corresponding variance and covariance expressions is required. We will rely on the method of normalized inverse probability weighting (IPWN, Ko and Wahed, 2012) to construct unbiased estimator of strategy means. Although in this paper we focus on sample size formula for a continuous endpoint, the formulas developed apply equally for designs with a binary endpoint.

Consider Design 1 described in Section 1 (Figure 1). Contrary to the counterfactual variables defined above, the observed data for this design consists of i.i.d (independent and identically distributed) random variables, $(X_{ji},R_i{Z}_{ki},(1-R_i)Z_{li}^{\prime },Y_i)$ where X_ji = 1, if the i^th patient is randomized to A_j; 0 otherwise. Y_i is the observed outcome for the i^th individual, R_i is the indicator for initial response, R_i = 1 if the i^th patient responded to initial therapy, 0, otherwise; Z_ki is the indicator for receiving B_k, i.e. Z_ki = 1 if subject i is randomized to receive B_k after responding to the first-stage treatment, 0, otherwise; similarly, $Z_{li}^{\prime }$ is the indicator for receiving C_l. We make the usual assumptions of causal inference to construct consistent estimators for μ_jkl [15]. They are:

• A1
  Consistency: A patient’s counterfactual outcome under the observed intervention (exposure) and the observed outcome agree. In the SMAR trial considered here,

  $$R_i=X_{1i}{R}_{1i}+(1-X_{1i})R_{2i},$$ (3)

  and

  $$Y_i=X_{1i}[R_{1i}{Y}_i(A_1{B}_1)+(1-R_{1i})Y_i(A_1{C}_1)]+(1-X_{1i})[R_{2i}{Y}_i(A_2{B}_1)+(1-R_{2i})Y_i(A_2{C}_2)],$$ (4)

  where R_1i and R_2i are indicators for counterfactual response to A₁ and A₂, respectively. The consistency assumption (CA) allows us to connect counterfactual and observed data.
• A2Sequential Randomization Assumption: The probability of a particular treatment allocation at stage a at a treatment time k does not depend on the counterfactual outcome given observed data up to but not including stage k randomization. This assumption follows since treatments are assigned randomly at each stage.
• A3Positivity: There is a non-zero probability of receiving any level of intervention for every combination of values of interventions.

Under these assumptions, we define the normalized weighted inverse probability estimator for strategy mean μ_jkl is given by

$${\hat{\mu }}_{jkl}^{IPWN}=\frac{{\sum }_{i=1}^n{W}_{jkli}{Y}_i}{{\sum }_{i=1}^n{W}_{jkli}},$$ (5)

where $W_{jkli}=X_{ji}\{\frac{R_i{Z}_{ki}}{P_k}+\frac{(1-R_i)Z_{li}^{\prime }}{Q_l}\}$, X_ji is the assignment indicator for first-stage treatment A_j; P_k and Q_l are probabilities of second treatment assignment for responders and non-responders, respectively.

Estimator (5) is similar to that in Ko and Wahed (2012) (Section 3.3) except that it treats the group sample sizes in Stage 1 as random rather than being treated as fixed. This is more reasonable because the group sizes in Stage 1 is determined through randomization. The IPWN estimator, ${\hat{\mu }}_{jkl}^{IPWN}$, defined in Equation (5) is consistent and asymptotically normal. This can be shown as follows. We can write,

$$\sqrt{n}({\hat{\mu }}_{jkl}^{IPWN}-{\mu }_{jkl})=\sqrt{n}[\frac{{\sum }_{i=1}^n{W}_{jkli}{Y}_i}{{\sum }_{i=1}^n{W}_{jkli}}-{\mu }_{jkl}]=n^{-1/2}\frac{{\sum }_{i=1}^n{W}_{jkli}(Y_i-{\mu }_{jkl})}{\frac{1}{n}{\sum }_{i=1}^n{W}_{jkli}}.$$

By the weak law of large numbers, $\frac{1}{n}{\sum }_{i=1}^n{W}_{jkli}\stackrel{P}{\to }\frac{1}{{\kappa }_j}$ where κ_j is the inverse of the randomization probability to A_j (i.e., ${\kappa }_j=\frac{1}{P(X_{ji}=1)}$). This follows from the fact that W_jkli’s are i.i.d random variables with expectation, $\mathrm{E}\{W_{jkli}\}=\mathrm{E}\left[\mathrm{E}\right[\{\frac{R_i{Z}_{1i}}{P_k}+\frac{(1-R_i)Z_{1i}^{\prime }}{Q_l}\}{X}_{ji}]|R_i,X_{ji}]=\mathrm{E}{X}_{ji}\mathrm{E}[\{\frac{R_i{Z}_{1i}}{P_k}+\frac{(1-R_i)Z_{1i}^{\prime }}{Q_l}|R_i,X_{ji}\}]=\mathrm{E}[X_{ji}\mathrm{E}\{R_i+(1-R_i)|R_i,X_{ji}\}]=\mathrm{E}[X_{ji}]=P(X_{ji}=1)=\frac{1}{{\kappa }_j}$. Also, by the central limit theorem, $n^{-1/2}{\sum }_{i=1}^n{W}_{jkli}(Y_i-{\mu }_{jkl})\stackrel{d}{\to }N(0,\frac{{\sigma }_{jkl}^2}{{\kappa }_j^2})$, where ${\sigma }_{jkl}^2$ is given in Equation (7) below. Therefore, by Slutsky’s theorem, $\sqrt{n}({\hat{\mu }}_{jkl}^{IPWN}-{\mu }_{jkl})$ is asymptotically equivalent in distribution to $n^{-1/2}{\kappa }_j{\sum }_{i=1}^n{W}_{jkli}(Y_i-{\mu }_{jkl})$ which is normally distributed as $N(0,{\sigma }_{jkl}^2)$. It can also be shown that,

$$\sqrt{n}({\hat{\mu }}_{jkl}^{IPWN}-{\mu }_{jkl})=n^{-1/2}\sum _{i=1}^n{\psi }_{jkli}+o_p(1),$$ (6)

where ψ_jkli = κ_jW_jkli(Y_i − μ_jkl) is the influence function of the estimator ${\hat{\mu }}_{jkl}^{IPWN}$ and o_p(1) is a term that converges to zero in probability. Therefore, the asymptotic variance of $\sqrt{n}({\hat{\mu }}_{jkl}^{IPWN}-{\mu }_{jkl})$ is given by,

$${\sigma }_{jkl}^2={\kappa }_j[\frac{{\pi }_j}{P_k}\{{\sigma }_{A_j{B}_k}^2+{(1-{\pi }_j)}^2{({\mu }_{A_j{B}_k}-{\mu }_{A_j{C}_l})}^2\}+\frac{1-{\pi }_j}{Q_l}\{{\sigma }_{A_j{C}_l}^2+{\pi }_j^2{({\mu }_{A_j{B}_k}-{\mu }_{A_j{C}_l})}^2\}],$$ (7)

where ${\sigma }_{A_j{B}_k}^2$ and ${\sigma }_{A_j{C}_l}^2$ are variances of the outcome in the population of patients who received the sequence of treatments A_jB_k and A_jC_l, respectively; μ_AjBk and μ_AjCl are defined as before. Details for derivation of variance of strategy mean $({\hat{\mu }}_{111}^{IPWN})$ and covariance between strategy means (${\hat{\mu }}_{111}^{IPWN}$ and ${\hat{\mu }}_{112}^{IPWN}$) is shown in Appendix B.

Overall Sample Size

The hypothesis of interest is whether there is a strategy-specific mean difference. The null hypothesis is H₀ : μ₁₁₁=μ₁₁₂=μ₁₂₁=μ₁₂₂=μ₂₁₁=μ₂₁₂=μ₂₂₁=μ₂₂₂, which is written as a linear equation H₀ : Cμ=0, where

$$C=\left[\begin{array}{cccccccc}\hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}\right],$$

and μ = [μ₁₁₁, μ₁₁₂, μ₁₂₁, μ₁₂₂, μ₂₁₁, μ₂₁₂, μ₂₂₁, μ₂₂₂]^T. Under the null hypothesis, the statistic nμ̂^TC^T[CΣ̂C^T]⁻¹Cμ̂ follows a central chi-square distribution with degree of freedom equal to 7, the number of rows of the contrast matrix C. Here μ̂ and Σ̂ denote estimated mean vector and covariance matrix given by,

$${\hat{\mu }}^T=[{\hat{\mu }}_{111},{\hat{\mu }}_{112},{\hat{\mu }}_{121},{\hat{\mu }}_{122},{\hat{\mu }}_{211},{\hat{\mu }}_{212},{\hat{\mu }}_{221},{\hat{\mu }}_{222}],$$

$$\hat{\mathrm{\Sigma }}=\left[\begin{array}{cc}\hfill {\hat{\mathrm{\Sigma }}}_1\hfill & \hfill \tilde{0}\hfill \\ \hfill \tilde{0}\hfill & \hfill {\hat{\mathrm{\Sigma }}}_2\hfill \end{array}\right],$$

where

$${\hat{\mathrm{\Sigma }}}_1=\left[\begin{array}{cccc}\hfill {\hat{\sigma }}_{111}^2\hfill & \hfill {\hat{\sigma }}_{111,112}\hfill & \hfill {\hat{\sigma }}_{111,121}\hfill & \hfill {\hat{\sigma }}_{111,122}\hfill \\ \hfill {\hat{\sigma }}_{112,111}\hfill & \hfill {\hat{\sigma }}_{112}^2\hfill & \hfill {\hat{\sigma }}_{112,121}\hfill & \hfill {\hat{\sigma }}_{112,122}\hfill \\ \hfill {\hat{\sigma }}_{111,112}\hfill & \hfill {\hat{\sigma }}_{121,112}\hfill & \hfill {\hat{\sigma }}_{121}^2\hfill & \hfill {\hat{\sigma }}_{121,122}\hfill \\ \hfill {\hat{\sigma }}_{122,111}\hfill & \hfill {\hat{\sigma }}_{122,112}\hfill & \hfill {\hat{\sigma }}_{122,121}\hfill & \hfill {\hat{\sigma }}_{122}^2\hfill \end{array}\right],$$

$${\hat{\mathrm{\Sigma }}}_2=\left[\begin{array}{cccc}\hfill {\hat{\sigma }}_{211}^2\hfill & \hfill {\hat{\sigma }}_{211,212}\hfill & \hfill {\hat{\sigma }}_{211,221}\hfill & \hfill {\hat{\sigma }}_{211,222}\hfill \\ \hfill {\hat{\sigma }}_{212,211}\hfill & \hfill {\hat{\sigma }}_{212}^2\hfill & \hfill {\hat{\sigma }}_{212,221}\hfill & \hfill {\hat{\sigma }}_{212,222}\hfill \\ \hfill {\hat{\sigma }}_{211,212}\hfill & \hfill {\hat{\sigma }}_{221,212}\hfill & \hfill {\hat{\sigma }}_{221}^2\hfill & \hfill {\hat{\sigma }}_{221,222}\hfill \\ \hfill {\hat{\sigma }}_{222,211}\hfill & \hfill {\hat{\sigma }}_{222,212}\hfill & \hfill {\hat{\sigma }}_{222,221}\hfill & \hfill {\hat{\sigma }}_{222}^2\hfill \end{array}\right],$$

$$\tilde{0}=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],$$

where μ̂_jkl is defined in Equation (7), ${\hat{\sigma }}_{jkl}^2$ is obtained by substituting estimates of parameters on the RHS in Equation (7). For example,

$$\widehat{\mathit{\text{var}}({\hat{\mu }}_{111})}=\frac{{\hat{\kappa }}_1}{n}[\frac{{\hat{\pi }}_1}{{\hat{P}}_1}\{{\hat{\sigma }}_{A_1{B}_1}^2+{({\hat{\mu }}_{111}-{\hat{\mu }}_{A_1{B}_1})}^2\}+\frac{(1-{\hat{\pi }}_1)}{{\hat{Q}}_1}\{{\tilde{\sigma }}_{A_1{C}_1}^2+{({\hat{\mu }}_{111}-{\hat{\mu }}_{A_1{C}_1})}^2\}],$$

where

$${\hat{\kappa }}_1=\frac{n}{{\sum }_{i=1}^n{X}_{1i}},$$

$${\hat{\pi }}_1=\frac{{\sum }_{i=1}^n{X}_{1i}{R}_i}{{\sum }_{i=1}^n{X}_{1i}},$$

$${\hat{\mu }}_{A_1{B}_1}=\frac{{\sum }_{i=1}^n{X}_{1i}{R}_i{Z}_{1i}{Y}_i}{{\sum }_{i=1}^n{X}_{1i}{R}_i{Z}_{1i}},$$

$${\hat{\sigma }}_{A_1{B}_1}^2=\frac{{\sum }_{i=1}^n{(X_{1i}{R}_i{Z}_{1i}{Y}_i-{\hat{\mu }}_{A_1{B}_1})}^2}{({\sum }_{i=1}^n{X}_{1i}{R}_i{Z}_{1i})({\sum }_{i=1}^n{X}_{1i}{R}_i{Z}_{1i}-1)},$$

$${\hat{Q}}_1=\frac{{\sum }_{i=1}^n{X}_{1i}(1-R_i)Z_{1i}^{\prime }}{{\sum }_{i=1}^n{X}_{1i}(1-R_i)},$$

and

$${\hat{P}}_1=\frac{{\sum }_{i=1}^n{X}_{1i}{R}_i{Z}_{1i}}{{\sum }_{i=1}^n{X}_{1i}{R}_i}.$$

Under the alternative hypothesis, the test statistic follows a non-central chi-squared distribution with the same degrees of freedom and a non-centrality parameter λ, where

$$\lambda =n{\mu }^T{C}^T{[C\mathrm{\Sigma }{C}^T]}^{-1}C\mu .$$

Consequently, a straightforward manipulation leads to a sample size formula,

$$n=\frac{\lambda }{{\mu }^T{C}^T{[C\mathrm{\Sigma }{C}^T]}^{-1}C\mu }.$$ (8)

To use the sample size formula in Equation (8), for a given power, we note that the power of the Wald test is the probability that we reject the null hypothesis, i.e., the probability that the test statistic is greater than the critical value. Thus,

$$\mathit{\text{power}}=P({\chi }_{df=7}^2(\lambda )\ge {\chi }_{df=7,\alpha }^2)=1-P({\chi }_{df=7}^2(\lambda )\le {\chi }_{df=7,\alpha }^2),$$ (9)

where α is the level of significance of the test, and ${\chi }_{df=7,\alpha }^2$ is the 100(1 − α)^th percentile of central χ² distribution with 7 degrees of freedom. For a given power and α, we can solve Equation (9) for λ. Having obtained λ, the sample size needed for achieving a given power is obtained by plugging in appropriate strategy means under the alternative hypothesis and their assumed variance-covariance matrix into the sample size expression above.

The knowledge of subgroup means and variances in the population will allow the computation of covariance terms. Suppose that the investigator wants to compare eight treatment strategies by testing the null hypothesis H₀ : μ₁₁₁ = μ₁₁₂ = μ₁₂₁ = μ₁₂₂ = μ₂₁₁ = μ₂₁₂ = μ₂₂₁ = μ₂₂₂ against the alternative that at least one pair is different. From the knowledge in the research area, the investigator expects that those who receive A₁ or A₂, responds and receives B₁ or does not respond and receives C₂ will have mean responses μ_A1B1 = μ_A2B1 = μ_A1C2 = μ_A2C2 = 15 and the group of individuals following any other paths of treatment will have mean response equal to 20. The variation of responses within these groups are expected to be ${\sigma }_{A_j{B}_k}^2=6^2$ and ${\sigma }_{A_j{C}_l}^2=8^2$, j, k, l = 1, 2.

Then, assuming 50% expected response in both A₁ and A₂ arms (π₁ = 0.5, π₂ = 0.5) and equal probability of randomization $({\kappa }_1=\frac{1}{1/2}=2,P_1=1/2,Q_1=1/2)$, we obtain μ₁₁₁ = π₁μ_A1B1 + (1 − π₁)μ_A1C1 = 17.5, μ₁₁₂ = π₁μ_A1B1 + (1 − π₁)μ_A1C2 = 15.0, μ₁₂₁ = π₁μ_A1B2 + (1 − π₁)μ_A1C1 = 21.0, μ₁₂₂ = π₁μ_A1B2 + (1 − π₁)μ_A1C2 = 18.5, μ₂₁₁ = π₂μ_A2B1 + (1 − π₂)μ_A2C1 = 17.5, μ₂₁₂ = π₂μ_A2B1 + (1 − π₂)μ_A2C2 = 15.0, μ₂₂₁ = π₂μ_A2B2 + (1 − π₂)μ_A2C1 = 17.5, μ₂₂₂ = π₂μ_A2B2 + (1 − π₂)μ_A2C2 = 15.0; and

$$\mathrm{\Sigma }=\left[\begin{array}{cccccccc}\hfill 225\hfill & \hfill 72\hfill & \hfill 123\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 72\hfill & \hfill 200\hfill & \hfill 0\hfill & \hfill 128\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 123\hfill & \hfill 0\hfill & \hfill 204\hfill & \hfill 79\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 128\hfill & \hfill 79\hfill & \hfill 249\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 225\hfill & \hfill 72\hfill & \hfill 123\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 72\hfill & \hfill 200\hfill & \hfill 0\hfill & \hfill 128\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 123\hfill & \hfill 0\hfill & \hfill 204\hfill & \hfill 79\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 128\hfill & \hfill 79\hfill & \hfill 249\hfill \end{array}\right].$$

Using C from the previous page (Page 9), we obtain

$${\mu }^T{C}^T{[C\mathrm{\Sigma }{C}^T]}^{-1}C\mu =0.206.$$

Now, if the investigator wants to power the study at 80% with α = 0.05, we solve

$$0.80=1-P({\chi }_{df=7}^2(\lambda )\le {\chi }_{df=7,\alpha }^2)$$

to obtain λ = 14.35. Then the sample size required for this case would be

$$n=\frac{14.350}{0.206}=69.66\approx 70.$$

4. Powering Pairwise Comparisons

Above we developed a sample size formula for a global test that provides evidence that there are differences among at least one pair of strategy means. Next, it is natural to focus on pairwise comparisons and ask which strategy means are different. A popular two-sample pairwise test is the t-test. A sample size based on the usual t-test would not apply directly since the assumption of independence among strategy means does not hold. When strategies share first stage treatment, a pairwise treatment comparison should consider the between-strategy covariances in the traditional t-test based sample size formula. Suppose we are interested in the sample size of a test that truly rejects the null hypotheses at a pre-specified level of significance (α) and a given power. For instance, there are 8 regimes and 28 pairwise comparisons for Design 1. One possible pairwise comparison would be,

$$H_0:{\mu }_{111}-{\mu }_{112}={\delta }_1.$$

For each test different sample sizes are required to detect a difference between each pairwise comparison. To control type I error, Bonferroni correction can be used. That is, for a two-sided test the level of significance for each hypothesis will be α/g, where g is the total number of pairwise comparisons. The aim is to compute the sample sizes for each pairwise comparison and then select maximum of the set of sample sizes that powers a test to identify difference between strategy means. The sample size formula that accounts dependency among strategy means is,

$$n=\frac{[{\sigma }_{jkl}^2+{\sigma }_{j\prime k\prime l\prime }^2-2{\sigma }_{jkl,j\prime k\prime l\prime }]{[Z_{1-\alpha /2g}+Z_{1-\beta }]}^2}{{[{\mu }_{jkl}-{\mu }_{j\prime k\prime l\prime }]}^2},j,k,l=1,2$$ (10)

where ${\sigma }_{jkl}^2,{\sigma }_{j\prime k\prime l\prime }^2$, and σ_{jkl,j′k′l′} are obtained using Equations (7) and (11); μ_jkl and μ_j′k′l′ are the strategy means under alternative hypothesis. If there is no overlap between strategy means that do not share the same initial treatments, the between-strategy means covariance is zero and the sample size formula (10) would mimic the one required for independent two-sample t-test.

Equation (10) has a more general use than it apparently implies. For example, suppose prior to designing the trial, researchers focus on g₁ ≤ g specific pairwise comparisons. Then the sample size for pairwise comparisons can be calculated using a level of significance $\frac{\alpha }{g_1}$ to ensure a pairwise comparison of g₁ pairs. Since the variance-covariance formula depends on the randomization probabilities, the researcher could potentially use randomization probabilities that allocate more observations to the strategies of interest. Other (g − g₁) pairwise comparisons could remain unpowered but essentially provide valuable information for future studies.

The methods described so far (in Section 3 and above) are explained via Design 1, however, the formulas can be applied to Designs 2 and 3. For example, in Design 2, there are no second stage randomization for responders. Therefore, we make the following simple modifications to make the formula applicable to Design 2. Set Y (A_j) as the counterfactual outcome for those who received A_j and responded, and let μ_Aj and ${\sigma }_{A_j}^2$ be the corresponding mean and variance of Y (A_j), j = 1, 2. As mentioned in Section 3, there are only four treatment strategies here, namely, A₁C₁, A₁C₂, $A_2{C}_1^{\prime }$, and $A_2{C}_2^{\prime }$. Therefore, the mean vector is μ = (μ₁₁, μ₁₂, μ₂₁, μ₂₂)^T where for example, μ₁₁ = π₁μ_A1 + (1 − π₁)μ_A1C1. Note that μ_A1C1 is used to indicate the mean of the population who receive A₁ as initial and C₁ as the second stage treatments. Similarly, the covariance matrix is

$$\mathrm{\Sigma }=\left[\begin{array}{cccc}\hfill {\sigma }_{11}^2\hfill & \hfill {\sigma }_{11,22}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\sigma }_{12,11}\hfill & \hfill {\sigma }_{12}^2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\sigma }_{21}^2\hfill & \hfill {\sigma }_{21,22}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\sigma }_{22,21}\hfill & \hfill {\sigma }_{22}^2\hfill \end{array}\right],$$

where

$${\sigma }_{1l}^2={\kappa }_1[{\pi }_1[{\sigma }_{A_1}^2+{(1-{\pi }_1)}^2{({\mu }_{A_1}-{\mu }_{A_1{C}_l})}^2]+\frac{1-{\pi }_1}{Q_l}({\sigma }_{A_1{C}_l}^2+{\pi }_1^2{({\mu }_{A_1}-{\mu }_{A_1{C}_l})}^2],$$

$${\sigma }_{2l}^2={\kappa }_2[{\pi }_2[{\sigma }_{A_2}^2+{(1-{\pi }_2)}^2{({\mu }_{A_2}-{\mu }_{A_2{C}_l^{\prime }})}^2]+\frac{1-{\pi }_2}{Q_l}({\sigma }_{A_2{C}_l^{\prime }}^2+{\pi }_2^2{({\mu }_{A_2}-{\mu }_{A_2{C}_l^{\prime }})}^2],$$

$${\sigma }_{11,12}={\kappa }_1{\pi }_1[{\sigma }_{A_1}^2+{(1-{\pi }_1)}^2({\mu }_{A_1}-{\mu }_{A_1{C}_1})({\mu }_{A_1}-{\mu }_{A_1{C}_2})],$$

$${\sigma }_{21,22}={\kappa }_2{\pi }_2[{\sigma }_{A_2}^2+{(1-{\pi }_2)}^2({\mu }_{A_2}-{\mu }_{A_2{C}_1^{\prime }})({\mu }_{A_2}-{\mu }_{A_2{C}_2^{\prime }})].$$

These formulas are obtained from the variance/covariance formulas for Design 1. For example, ${\sigma }_{1l}^2$ is the same as the RHS of Equation (7) with j = 1, k = 1, P₁ = 1, ${\sigma }_{A_1{B}_1}^2={\sigma }_{A_1}^2$ and μ_A1B1 = μ_A1. The required sample size for testing the null hypothesis H₀: μ₁₁ = μ₁₂ = μ₂₁ = μ₂₂ at level α and power 1 − β against an alternative specified by the subgroup means μ_A1, μ_A1C1, μ_A1C2, μ_A1, ${\mu }_{A_2{C}_1^{\prime }},{\mu }_{A_2{C}_2^{\prime }}$ is then given by formula (8) with

$$C=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}\right],$$

and λ, the non-centrality parameter, given by the solution to the equation

$$P({\chi }_{df=3}^2(\lambda )\le {\chi }_{df=3,\alpha }^2)=\beta .$$

Appropriate modifications can be used for Design 3 in a similar manner.

5. Simulation Study and Results

To evaluate the performance of the overall sample size formula, we conducted a number of simulations to see if the empirical power for detecting the alternative hypothesis is close to the nominal power. We presented four scenarios for each of the three designs in Tables 1, 2 and 3 by varying the nominal power, response rates and probabilities of second treatment assignment for responders (P_k) and non-responders (Q_l). For each subject in the population, Y_i(A_jB_k) and Y_i(A_jC_l) were generated from normal distribution with means μ_AjBk and μ_AjCl, and variances ${\sigma }_{A_j{B}_k}^2$ and ${\sigma }_{A_j{C}_l}^2$, respectively for j, k, l = 1, 2. Correspondingly, in Designs 2 and 3 for each individual, Y_i(A_j) was generated from normal distribution, with means μ_Aj. The indicator X_ji was generated from a Bernoulli distribution with probability 0.5. Indicators Z_k and $Z_l^{\prime }$ were generated from a Bernoulli distribution with probability P_k and Q_l for responders and non-responders, respectively. The response status R_i was generated from a Bernoulli distribution with probability (response rate) π₁ for treatment A₁ and π₂ for treatment A₂ and whenever applicable (Design 3), from a Bernoulli(π₃) distribution for treatment A₃. For Design 1, the outcome variable Y_i is then generated using Equation (4). For Design 2, we used the same equation except that Y_i(A₁B₁) and Y_i(A₂B₁) is replaced by Y_i(A₁) and Y_i(A₂), respectively. Similar modification was made for Design 3. For each design and for each scenario we generated 10000 Monte-Carlo samples using the three designs.

Table 1.

Sample size computation and simulation of empirical power (# replications=10000) for Design 1 where Q₁ = 0.5, subgroup means: μ_AjB1 = μ_AjC2 = 15, μ_AjC1 = 20, μ_AjB2 = 22; subgroup variances: ${\sigma }_{A_j{B}_k}^2=6^2,{\sigma }_{A_j{C}_l}^2=8^2$, for j, k, l = 1, 2. Hypothesis of interest is H₀ : μ₁₁₁=μ₁₁₂=μ₁₂₁=μ₁₂₂=μ₂₁₁=μ₂₁₂=μ₂₂₁=μ₂₂₂; α = 0.05.

Scenario	π1	π2	P1	Nominal Power	Overall Sample Size	Empirical Power	Effect Size (Mahalanobis Distance)
1	0.5	0.5	0.5	0.8	70	0.84	0.206
	0.5	0.5	0.7	0.8	79	0.85	0.182
	0.5	0.5	0.5	0.9	89	0.92	0.206
	0.5	0.5	0.8	0.9	120	0.92	0.152
2	0.2	0.5	0.5	0.8	83	0.82	0.172
	0.2	0.5	0.7	0.8	92	0.83	0.156
	0.2	0.5	0.5	0.9	106	0.9	0.172
	0.2	0.5	0.8	0.9	134	0.92	0.136
3	0.7	0.5	0.5	0.8	62	0.85	0.231
	0.7	0.5	0.7	0.8	71	0.85	0.201
	0.7	0.5	0.5	0.9	79	0.92	0.231
	0.7	0.5	0.7	0.9	91	0.92	0.201
4	0.2	0.7	0.5	0.8	72	0.84	0.198
	0.2	0.7	0.7	0.8	82	0.84	0.176
	0.2	0.7	0.5	0.9	92	0.91	0.198
	0.2	0.7	0.7	0.9	104	0.92	0.176

Alternative is true with means: Scenario 1: μ₁₁₁ = 17.5, μ₁₁₂ = 15.0, μ₁₂₁ = 21.0, μ₁₂₂ = 18.5, μ₂₁₁ = 17.5, μ₂₁₂ = 15.0, μ₂₂₁ = 21.0, μ₂₂₂ = 18.5

Scenario 2: μ₁₁₁ = 19.0, μ₁₁₂ = 15.0, μ₁₂₁ = 20.4, μ₁₂₂ = 16.4, μ₂₁₁ = 17.5, μ₂₁₂ = 15.0, μ₂₂₁ = 21.0, μ₂₂₂ = 18.5

Scenario 3: μ₁₁₁ = 16.5, μ₁₁₂ = 15.0, μ₁₂₁ = 21.4, μ₁₂₂ = 19.9, μ₂₁₁ = 17.5, μ₂₁₂ = 15.0, μ₂₂₁ = 21.0, μ₂₂₂ = 18.5

Scenario 4: μ₁₁₁ = 19.0, μ₁₁₂ = 15.0, μ₁₂₁ = 20.4, μ₁₂₂ = 16.4, μ₂₁₁ = 16.5, μ₂₁₂ = 15.0, μ₂₂₁ = 21.4, μ₂₂₂ = 19.9

Table 2.

Sample size computation and simulation of empirical power (# replications=10000) for Design 2 where subgroup means: μ_A1 = 15, μ_A2 = 17, μ_A1C1 = 20, μ_A1C2 = 15, ${\mu }_{A_2{C}_1^{\prime }}=22,{\mu }_{A_2{C}_2^{\prime }}=15$; subgroup variances: ${\sigma }_{A_j}^2=6^2,{\sigma }_{A_1{C}_l}^2={\sigma }_{A_2{C}_l^{\prime }}^2=8^2$ for j, k, l = 1, 2. Hypothesis of interest is H₀ : μ₁₁=μ₁₂=μ₂₁=μ₂₂.

Scenario	π1	π2	Q1	Nominal Power	Overall Sample Size	Empirical Power	Effect Size (Mahalanobis Distance)
1	0.5	0.5	0.5	0.8	142	0.81	0.077
	0.5	0.5	0.7	0.8	156	0.82	0.069
	0.5	0.5	0.5	0.9	185	0.91	0.077
	0.5	0.5	0.9	0.9	344	0.92	0.041
2	0.2	0.5	0.5	0.8	130	0.81	0.084
	0.2	0.5	0.7	0.8	144	0.82	0.071
	0.2	0.5	0.5	0.9	169	0.91	0.084
	0.2	0.5	0.9	0.9	448	0.92	0.032
3	0.7	0.5	0.5	0.8	143	0.82	0.076
	0.7	0.5	0.7	0.8	143	0.83	0.076
	0.7	0.5	0.5	0.9	186	0.91	0.076
	0.7	0.5	0.9	0.9	241	0.93	0.059
4	0.7	0.2	0.5	0.8	94	0.82	0.116
	0.7	0.2	0.7	0.8	88	0.84	0.123
	0.7	0.2	0.5	0.9	122	0.9	0.116
	0.7	0.2	0.9	0.9	131	0.94	0.108

Alternative is true with means: Scenario 1: μ₁₁ = 17.5, μ₁₂ = 15.0, μ₂₁ = 19.5, μ₂₂ = 16.0

Scenario 2: μ₁₁ = 19.0, μ₁₂ = 15.0, μ₂₁ = 19.5, μ₂₂ = 16.0

Scenario 3: μ₁₁ = 16.5, μ₁₂ = 15.0, μ₂₁ = 19.5, μ₂₂ = 16.0

Scenario 4: μ₁₁ = 16.5, μ₁₂ = 15.0, μ₂₁ = 21.0, μ₂₂ = 15.4

Table 3.

Sample size computation and simulation of empirical power (# replications=10000) for Design 3 where subgroup means: μ_A1 = 15, μ_A2 = 17, μ_A3 = 19, μ_A1A3 = μ_A2A3 = μ_A3A2 = 15, μ_A1A2 = 20, μ_A2A1 = 22, μ_A3A1 = 24; subgroup variances: ${\sigma }_{A_j}^2=6^2,{\sigma }_{A_j{A}_l}^2=8^2$ for j ≠ l; j, l = 1, 2, 3. Response rate for induction treatment A₃ is assumed to be 50%. Hypothesis of interest is H₀ : μ₁₂ = μ₁₃ = μ₂₁ = μ₂₃ = μ₃₁ = μ₃₂.

Scenario	π1	π2	Nominal Power	Overall Sample Size	Empirical Power	Effect Size (Mahalanobis Distance)
1	0.5	0.5	0.8	108	0.83	0.119
	0.2	0.5	0.8	111	0.83	0.116
	0.5	0.5	0.9	139	0.91	0.119
	0.2	0.5	0.9	142	0.91	0.116
2	0.2	0.2	0.8	95	0.84	0.135
	0.2	0.6	0.8	116	0.84	0.110
	0.2	0.2	0.9	122	0.92	0.135
	0.2	0.6	0.9	149	0.91	0.110
3	0.3	0.5	0.8	111	0.83	0.116
	0.3	0.6	0.8	116	0.82	0.110
	0.3	0.5	0.9	142	0.91	0.116
	0.3	0.6	0.9	149	0.92	0.110
4	0.4	0.5	0.8	110	0.83	0.117
	0.4	0.6	0.8	115	0.82	0.111
	0.4	0.5	0.9	141	0.92	0.117
	0.4	0.6	0.9	148	0.91	0.111

Alternative is true with means: Scenario 1: μ₁₂ = 17.5, μ₁₃ = 15.0, μ₂₁ = 19.5, μ₂₃ = 16.0, μ₃₁ = 21.5, μ₃₂ = 17.0

Scenario 2: μ₁₂ = 19.0, μ₁₃ = 15.0, μ₂₁ = 21.0, μ₂₃ = 15.4, μ₃₁ = 21.5, μ₃₂ = 17.0

Scenario 3: μ₁₂ = 18.5, μ₁₃ = 15.0, μ₂₁ = 19.5, μ₂₃ = 16.0, μ₃₁ = 21.5, μ₃₂ = 17.0

Scenario 4: μ₁₂ = 18.0, μ₁₃ = 15.0, μ₂₁ = 19.5, μ₂₃ = 16.0, μ₃₁ = 21.5, μ₃₂ = 17.0

Tables 1, 2 and 3 demonstrate sample size computation for different scenarios by assuming certain values for population parameters. Tables 4 and 5 show the pairwise sample size computation for Designs 2 and 3. Design 1 assumes subgroup means: μ_AjB1 = μ_AjC2 = 15, μ_AjC1 = 20, μ_AjB2 = 22; subgroup variances: ${\sigma }_{A_j{B}_k}^2=6^2,{\sigma }_{A_j{C}_l}^2=8^2$, for j, k, l = 1, 2. Subgroup variances are assumed to be the same for all designs considered. Depending on a specific design and scenario considered, the following range of response proportions π_j’s are assumed: 0.2, 0.3, 0.5, 0.6 and 0.7. Similarly, depending on a specific design the following P₁ and Q₁ are assumed. Probability of treatment assignment for responders, P₁, is assumed to be 0.5, 0.7, 0.9 and 1. For non-responders, Q₁(= 1 − Q₂), is assumed to be 0.5, 0.7, 0.9. Design 2 assumes the following subgroup means: μ_A1B1 = 15, μ_A2B1 = 17, μ_AjC2 = 15, μ_A1C1 = 20, μ_A2C1 = 22, for j, k, l = 1, 2. Design 3 assumes the following subgroup means: μ_A1B1 = 15, μ_A2B1 = 17, μ_A3B1 = 19, μ_AjC2 = 15, μ_A1C1 = 20, μ_A2C1 = 22, μ_A3C2 = 24, for j, k, l = 1, 2, 3. The parameter values were chosen following those from Ko and Wahed [13]. The strategy means differ for each scenario in each table. In each scenario, having obtained the appropriate sample size using our formula, we evaluate the power of the Wald tests in rejecting the null hypothesis of no difference in treatment means when the strategies have different means. Effect sizes are common measures in psychology and other disciplines where they are useful in calculating and interpreting power. The magnitude of effect sizes would capture experimental effects by protecting guaranteed significance due to large sample size [12]. The effect size is computed using the Mahalanobis distance (MD). One useful property of the MD is that it takes into account the correlation in the data.

Table 4.

Pairwise sample size computation for Design 2. Subgroup means: μ_A1 = 15, μ_A2 = 17, μ_A1C1 = 20, μ_A1C2 = 15, ${\mu }_{A_2{C}_1^{\prime }}=22,{\mu }_{A_2{C}_2^{\prime }}=15$; subgroup variances: ${\sigma }_{A_j}^2=6^2,{\sigma }_{A_1{C}_l}^2={\sigma }_{A_2{C}_l^{\prime }}^2=8^2$ for j, k, l = 1, 2. Here π₁=0.5, π₂=0.5, Q₁=0.5, and power=0.8.

Hypothesis	Overall MC Adjusted Sample Size	Not Corrected for Multiple Comparison	δi
H1 : μ11−μ12=δ1	532	345	2.5
H2 : μ11−μ21=δ2	1107	717	−2.0
H3 : μ11−μ22=δ3	1882	1220	1.5
H4 : μ12−μ21=δ4	207	134	−4.5
H5 : μ12−μ22=δ5	4008	2598	−1.0
H6 : μ21−μ22=δ6	280	181	3.5

Table 5.

Pairwise sample size computation for Design 3. Subgroup means: μ_A1 = 15, μ_A2 = 17, μ_A3 = 19, μ_A1A3 = μ_A2A3 = μ_A3A2 = 15, μ_A1A2 = 20, μ_A2A3 = 22, μ_A3A2 = 24; subgroup variances: ${\sigma }_{A_j}^2=6^2,{\sigma }_{A_j{A}_l}^2=8^2$ for j ≠ l; j, l = 1, 2, 3. Here π₁ = 0.5, π₂ = 0.5, π₃ = 0.5, Q₁ = 0.5, and power=0.8. Second column provides sample size which powers all pairwise comparisons whereas the third column assumes that only three of the fifteen hypotheses are of interest.

Hypothesis	Overall MC Adjusted Sample Size	Partially MC Adjusted Sample Size	δi
H1 : μ12−μ13=δ1	941	690	2.5
H2 : μ12−μ21=δ2	1955	1435	−2.0
H3 : μ12−μ23=δ3	3326	2441	1.5
H4 : μ12−μ31=δ4	489	359	−4.0
H5 : μ12−μ32=δ5	30704	22535	0.5
H6 : μ13−μ21=δ6	366	269	−4.5
H7 : μ13−μ23=δ7	7082	5198	−1.0
H8 : μ13−μ31=δ8	176	129	−6.5
H9 : μ13−μ32=δ9	1819	1335	−2.0
H10 : μ21−μ23=δ10	494	362	3.5
H11 : μ21−μ31=δ11	1955	1435	−2.0
H12 : μ21−μ32=δ12	1228	901	2.5
H13 : μ23−μ31=δ13	247	182	−5.5
H14 : μ23−μ32=δ14	7339	5386	−1.0
H15 : μ31−μ32=δ15	314	230	4.5

The first row of Scenario 1 in Table 1 assumes strategy means μ₁₁₁ = 17.5 μ₁₁₂ = 15, μ₁₂₁ = 21, μ₁₂₂ = 18.5, μ₂₁₁ = 17.5, μ₂₁₂ = 15, μ₂₂₁ = 21, μ₂₂₂ = 18.5 when response rates π₁, π₂ were taken to be both 0.5; P₁ and Q₁ are assumed to be 0.5. Seventy subjects would be required to detect the resulting effect size of 0.21 with power 80% at α = 0.05. The empirical power is 85% which is slightly inflated compared to the nominal power of 80% used to compute the sample size. Row 3 of the same scenario shows that the empirical power of 92% is close to the nominal value of 90%. Similar patterns follow for all the rows in Scenarios 2, 3 and 4. If we observe across all scenarios (from 4 to 1), we note a small degree of increase in empirical power when P₁ increases.

The first row of Scenario 1 in Design 2 (Table 2) assumes strategy means μ₁₁ = 17.5, μ₁₂ = 15, μ₂₁ = 19.5, μ₂₂ = 16 when response rates π₁, π₂ were taken to be both 0.5; Q₁=0.5. In this case 142 subjects would be required to detect the resulting effect size of 0.08 with power 80% at α = 0.05. The empirical power is 81% which is very close to the nominal power of 80% used to compute the sample size. Row 4 of scenario 3 shows that the empirical power of 93% is slightly inflated compared to the nominal value of 90%. For various response rates, the empirical power for each case in scenarios 1 to 3 nearly attain the nominal power. This attests that the sample sizes calculated for Design 2 ensure enough power to detect differences among the four strategy means.

The first row of Scenario 1 in Design 3 (Table 3) assumes strategy means μ₁₂ = 17.5, μ₁₃ = 15, μ₂₁ = 19.5, μ₂₃ = 16, μ₃₁ = 21.5, μ₃₂ = 17 when response rates π₁, π₂, π₃ were taken to be all 0.5. 108 subjects would be required to detect the resulting effect size of 0.12 with power 80% at α = 0.05. The empirical power is 83% which is slightly larger than the nominal power of 80% used to compute the sample size. We note that for small changes in response rates, sometimes the sample sizes do not change or change only slightly. For example, row 4 of scenarios 2 and 3 have the same sample size (149). The sample size did not change as π₁ changed slightly from 0.2 to 0.3.

In many clinical trials testing of overall hypothesis may not be of primary interest, rather some or all of the pairwise comparisons are. To show how the sample size for a SMAR trial is determined in such cases, we present the sample sizes required for Design 2 when all six pairwise comparisons are powered simultaneously in the second column of Table 4. The third column provides the sample sizes when only individual tests are powered. For example, under the setting described in Table 4, Design 2 requires 4008 patients to power all pairwise comparisons. However, if the interest, for example, is in powering the single hypothesis H₀ : μ₁₁₁ = μ₁₁₂ leaving other pairs as exploratory, the trial could be conducted using a sample as small as 345. Similarly, Table 5 provides sample sizes for Design 3 when fifteen pairwise comparisons are powered simultaneously (Column 2) and when only three pairwise comparisons are considered (Column 3). From Column 2, Design 3 requires 30,704 patients (maximum of the sample sizes) to power all pairwise comparisons. However, if the interest is in powering only three pairwise hypotheses such as H₀ : μ₁₂ = μ₁₃, H₀ : μ₁₂ = μ₂₁, and H₀ : μ₁₂ = μ₂₃, the trial would require a sample size of 2,441. On the other hand, if the interest is only in comparing the three pairs, H₄, H₆, and H₈ then the sample size required will be n = 359.

Outcomes in the above simulation scenarios were generated from a normal distribution. We wanted to conduct the sensitivity of our formula to non-normal responses. To do this, we further generated data from Logistic (symmetric) and Gamma (skewed) distributions and calculated the empirical power based on the sample size calculated using Equation(8). Basically, we selected one row from each scenario of Tables 1 to 3 to perform sensitivity analysis of our formula using data from Logistic and Gamma distributions ensuring the same means and variances for the subpopulations and keeping all other parameters the same. From each table, we selected the first row for Scenarios 1 and 3 while we chose the fourth row for Scenarios 2 and 4. Therefore, the results presented in Table 6 have twelve rows in total. In general, the nominal power is maintained and is consistent across the three distributions. This shows that our sample size formula is robust to the misspecification of outcome distribution.

Table 6.

Robustness of the Sample Size Formula against misspecification of outcome distributions. For Design 1 the following parameter values were considered: Q₁ = 0.5, subgroup means: μ_AjB1 = μ_AjC2 = 15, μ_AjC1 = 20, μ_AjB2 = 22; subgroup variances: ${\sigma }_{A_j{B}_k}^2=6^2,{\sigma }_{A_j{C}_l}^2=8^2$, for j, k, l = 1, 2. The hypothesis tested is H₀ : μ₁₁₁=μ₁₁₂=μ₁₂₁=μ₁₂₂=μ₂₁₁=μ₂₁₂=μ₂₂₁=μ₂₂₂; α = 0.05. For Design 2 the following parameter values were considered: P₁ = 1, subgroup means: μ_A1 = 15, μ_A2 = 17, μ_A1C1 = 20, μ_A1C2 = 15, ${\mu }_{A_2{C}_1^{\prime }}=22,{\mu }_{A_2{C}_2^{\prime }}=15$; subgroup variances: ${\sigma }_{A_j}^2=6^2,{\sigma }_{A_1{C}_l}^2={\sigma }_{A_2{C}_l^{\prime }}^2=8^2$ for j, k, l = 1, 2. The hypothesis tested is H₀ : μ₁₁=μ₁₂=μ₂₁=μ₂₂. For Design 3 the following parameter values were considered: P₁ = 1, subgroup means: μ_A1 = 15, μ_A2 = 17, μ_A3 = 19, μ_A1A3 = μ_A2A3 = μ_A3A2 = 15, μ_A1A2 = 20, μ_A2A3 = 22, μ_A3A2 = 24; subgroup variances: ${\sigma }_{A_j}^2=6^2,{\sigma }_{A_j{A}_l}^2=8^2$ for j ≠ l; j, l = 1, 2, 3. Response rates to induction treatment A₃ is assumed to be 50%. The hypothesis tested is H₀ : μ₁₁=μ₁₃=μ₂₁=μ₂₃=μ₃₁=μ₃₂.

Design	Scenario	π1	π2	P1	Q1	Nominal Power	Overall Sample Size	Empirical Power: Normal	Empirical Power: Gamma	Empirical Power: Logistic
Design 1	1	0.5	0.5	0.5	0.5	0.8	70	0.84	0.86	0.86
	2	0.2	0.5	0.8	0.5	0.9	134	0.92	0.93	0.93
	3	0.7	0.5	0.5	0.5	0.8	62	0.85	0.86	0.87
	4	0.2	0.7	0.7	0.5	0.9	104	0.92	0.92	0.92
Design 2	1	0.5	0.5	-	0.5	0.8	142	0.81	0.83	0.82
	2	0.2	0.5	-	0.9	0.9	448	0.92	0.91	0.91
	3	0.7	0.5	-	0.5	0.8	143	0.82	0.85	0.83
	4	0.7	0.2	-	0.9	0.9	131	0.94	0.96	0.94
Design 3	1	0.5	0.5	-	0.5	0.8	108	0.83	0.86	0.85
	2	0.2	0.6	-	0.5	0.9	149	0.91	0.93	0.92
	3	0.3	0.5	-	0.5	0.8	111	0.83	0.86	0.85
	4	0.4	0.6	-	0.5	0.9	148	0.91	0.93	0.92

6. Discussion

Complex multi-stage diseases require decision-based multi-stage treatments depending on the response to prior-stage treatments. SMAR designs provide efficient and unbiased inference to compare staged strategies for complex conditions. We presented a sample size formula that is applicable for various SMAR designs to ensure adequately powered comparisons of these treatment strategies. The usual design is to randomize responders (or non-responders) to available treatments. A slight variation to that is a design where responders (or non-responders) would not be randomized any further in the second stage. Designs 2 and 3 are such examples. In Design 2, only the non-responders are randomized to C₁ or C₂ and $C_1^{\prime }$ or $C_2^{\prime }$ respectively depending on whether they received A₁ or A₂ in the first stage. Responders would stay on the same first stage treatment. Equivalently, responders will be randomized with probability 1 to whatever treatment they received in the first stage. There are four strategies resulting from this design and the sample size required to detect differences among the four strategies is computed. In Design 3 each patient is randomized to a set of treatments (A₁, A₂, A₃) in the first stage and these treatments are continued until they fail due to disease worsening. The patient is then re-randomized among a set of the same first stage treatments with the exception of the treatment s/he received initially. There are six strategies of interest in this design. We showed in the simulation how to compute sample size formula for this design and showed that the formula ensures nominal power under various scenarios involving many outcome distributions.

In contrast to our formula, Murphy’s [5] formula is not applicable to designs powering multi-strategy comparison or to designs comparing strategies that share the same initial treatments commonly referred to as shared-path strategies [17] or overlapping strategies [10]. Moreover, their formula requires specifying the variance of the response under the strategies being compared, although the effect sizes can be specified per standard deviations of mean difference assuming equal variance across strategies.

Dawson and Lavori [10, 11] provides a sample size formula for comparing pairs of overlapping or non-overlapping/treatment strategies based on semiparametric efficient variances. The formula requires one to specify the variance of the response under each strategy and the variance inflation factor, the latter depending on the coefficient of determinations based on the regression of counterfactual strategy response on stage-specific states. Correct specification of such quantities is difficult, if not impossible, in the absence of a similar SMAR trial. However, when correctly specified, Dawson and Lavori’s formula provide smaller sample sizes than those proposed in Murphy [5] or the ones provided here. One advantage of both Murphy [5] and Dawson and Lavori’s [10, 11] formula over our method is that they can be applied to compare strategies from SMAR trial with more than two stages. However, like Murphy’s formula, Dawson and Lavori’s formula also focuses on comparing pairs of treatment strategies.

The simplicity of our procedure compared to Dawson and Lavori [10] (even in the two-stage SMAR trial settings) relies on the specification of the parameters. Our formula requires one to specify sub-group-specific means and variances. Our sample size formula requires specification of subgroup means and variances for patients following different treatment paths. These parameters are usually available from observational studies or stage-specific individual non-SMAR trials. For example, there are many cancer clinical trials that compare frontline treatments (e.g. Estey et al. [18]). Even though such trials are terminated once the recruitment is over and the primary endpoint is observed or the trial period ends, patients are often followed and medication information (salvage treatments used) is collected for patients who become resistant to frontline therapy or for patients with disease progression. The collection of salvage treatment information is often done only for the purpose of safety, however, such information allows the researchers to obtain meaningful information on subgroup means and variances based on the salvage therapies received within each frontline treatments. Mental health research by its very nature, investigates sequences of treatments and hence the means and variances of responses under a particular treatment sequence are most likely to be available from observational studies or from electronic medical records. Fortunately, there are already existing SMAR trials in mental health (STAR*D [2], CATIE [19]) that can provide useful information on subgroups to be used in future trial design.

The Murphy [5] and Dawson and Lavori [10] methods require fewer unknown quantities to be specified compared to what is required by our formula, our parameters are basically means and variances of response among subpopulations. Generally, these parameters can be obtained from pilot studies, non-SMAR trials or observational studies. Therefore, these parameters are less likely to be mis-specified as compared to the parameters in Murphy’s [5] and Dawson and Lavori’s [10] methods. Moreover, our focus is to compare multiple treatment strategies for which specification of effect size does not necessarily reduce the number of unknown parameters.

Oetting et al. [9] sample size for comparing two strategies is derived under the assumption that response rates are the same across the two first stage treatments. While a sensitivity analysis was carried out in the simulation, this assumption may not be reasonable in practice. Finally, our formula does not address the issue of finding an optimal treatment strategy, which is a separate issue that is dealt with in Oetting et al. [9].

Use of Mahlanobis distance as an effect size measure in our analysis is to verify that the sample size increases with the increase in distance among the strategy means. Note that unlike standard effect size measures, Mahlanobis distance has no benchmark values to indicate large, small or moderate effect sizes. It should just be treated as a distance among multiple strategy means standardized for the variability.

Future research could investigate sample size formulas for various k-stage designs with emphasis on specific and meaningful number of strategies. Issues of missing data is another design concern in SMAR trials that needs to be addressed.

Appendix A: Influence function for μ̂_jkl

Equation (6) can be expanded as follows μ̂_jkl satisfies $g({\mu }_{jkl})=\frac{1}{n}{\sum }_{i=1}^n{W}_{jkli}(Y_i-{\hat{\mu }}_{jkl})=0$. Expanding with respect to μ_jkl,

$$\frac{1}{n}\sum _{i=1}^n{W}_{jkli}(Y_i-{\mu }_{jkl})-({\hat{\mu }}_{jkl}-{\mu }_{jkl})\frac{1}{n}\sum _{i=1}^n{W}_{jkli}=0$$

$$\frac{1}{n}\sum _{i=1}^n{W}_{jkli}(Y_i-{\mu }_{jkl})-({\hat{\mu }}_{jkl}-{\mu }_{jkl})(\frac{1}{n}\sum _{i=1}^n{W}_{jkli}-\frac{1}{{\kappa }_j})-({\hat{\mu }}_{jkl}-{\mu }_{jkl})\frac{1}{{\kappa }_j}=0.$$

This implies,

$$({\hat{\mu }}_{jkl}-{\mu }_{jkl})=\frac{1}{n}\sum _{i=1}^n\frac{1}{{\kappa }_j}{W}_{jkli}(Y_i-{\mu }_{jkl})-{\kappa }_j({\hat{\mu }}_{jkl}-{\mu }_{jkl})(\frac{1}{n}\sum _{i=1}^n(W_{jkli}-\frac{1}{{\kappa }_j}))$$

and

$$\sqrt{n}({\hat{\mu }}_{jkl}-{\mu }_{jkl})=n^{-1/2}\sum _{i=1}^n{\psi }_{jkli}-{\kappa }_j({\hat{\mu }}_{jkl}-{\mu }_{jkl})n^{-1/2}\sum _{i=1}^n(W_{jkli}-\frac{1}{{\kappa }_j}).$$

Now ${\hat{\mu }}_{jkl}\stackrel{p}{\to }{\mu }_{jkl}$, and hence μ̂_jkl − μ_jkl is o_p(1) and $n^{-1/2}{\sum }_{i=1}^n(W_{jkli}-\frac{1}{{\kappa }_j})$ is bounded in probability (O_p(1)) because of its convergence in distribution to normal distribution by central limit theorem. Therefore, the second term on the right is o_p(1).

Appendix B: Variance and covariance of strategy means

Following Ko and Wahed (2012), the variance formula in Equation (7) is derived as follows, ${\sigma }_{jkl}^2=\mathit{\text{var}}({\psi }_{jkli})=\mathit{\text{var}}({\kappa }_j{W}_{jkli}(Y_i-{\mu }_{jkl}))={\kappa }_j^{2}E{[W_{jkli}(Y_i-{\mu }_{jkl})]}^2$. This variance can be expressed in terms of subgroup-specific population parameters. For example, consider ${\hat{\mu }}_{111}^{IPWN}$. In this case, the weight is defined as $W_{111i}=X_{1i}\{\frac{R_i{Z}_{1i}}{P_1}+\frac{(1-R_i)Z_{1i}^{(\prime )}}{Q_1}\}$, and therefore, $W_{111i}^2=X_{1i}\{\frac{R_i{Z}_{1i}}{P_1^2}+\frac{(1-R_i)Z_{1i}^{\prime }}{Q_1^2}\}$ since the indicator variables X_1i, R_i, Z_1i and $Z_{1i}^{\prime }$ take values 0 or 1; the term $2\frac{R_i{Z}_{1i}(1-R_i)Z_{1i}^{\prime }}{P_1{Q}_1}$ disappears since a patient can only be a responder or a non-responder. Then, $E[W_{111i}^2{(Y_i-{\mu }_{111})}^2]=E\left[X_{1i}\right\{\frac{R_i{Z}_{1i}}{P_1^2}+\frac{(1-R_i)Z_{1i}^{\prime }}{Q_1^2}\left\}{(Y_i-{\mu }_{111})}^2\right]$. Under assumptions (A1)–(A3), using a series of conditional expectations, we can show that,

$$E[W_{111i}^2{(Y_i-{\mu }_{111})}^2]={\kappa }_1^{2}E\left[X_{1i}\right\{\frac{R_i{Z}_{1i}}{P_1^2}+\frac{(1-R_i)Z_{1i}^{\prime }}{Q_1^2}\left\}{(Y_i-{\mu }_{111})}^2\right]={\kappa }_1^{2}EE\left[X_{1i}\right\{\frac{R_i{Z}_{1i}}{P_1^2}\}{\{R_i{Y}_i(A_1{B}_1)+(1-R_i)Y_i(A_1{C}_1)-{\mu }_{111}\}}^2|R_i,X_{1i},Y_i(A_1{B}_1),Y_i(A_1{C}_1)]+{\kappa }_1^{2}EE[X_{1i}\left\{\frac{(1-R_i)Z_{1i}^{\prime }}{Q_1^2}\right\}{\{R_i{Y}_i(A_1{B}_1)+(1-R_i)Y_i(A_1{C}_1)-{\mu }_{111}\}}^2|R_i,X_{1i},Y_i(A_1{B}_1),Y_i(A_1{C}_1)]={\kappa }_1^{2}E\left[X_{1i}\right\{\frac{R_i}{P_1^2}\}{\{R_i{Y}_i(A_1{B}_1)-{\mu }_{111}\}}^{2}E[Z_{1i}|R_i,X_{1i},Y_i(A_1{B}_1)]]+{\kappa }_1^{2}E[X_{1i}\left\{\frac{(1-R_i)}{Q_1^2}\right\}{\{(1-R_i)Y_i(A_1{C}_1)-{\mu }_{111}\}}^{2}E[Z_{1i}^{\prime }|R_i,X_{1i},Y_i(A_1{C}_1)\left]\right]={\kappa }_1^2{P}_{1}E[\frac{X_{1i}}{P_1^2}E[R_i{Y}_i^2(A_1{B}_1)-2{\mu }_{111}\{R_i{Y}_i(A_1{B}_1)\}+{\mu }_{111}^2|R_i,X_{1i}]]+{\kappa }_1^2{Q}_{1}E[\frac{X_{1i}}{Q_1^2}E[(1-R_i)Y_i^2(A_1{C}_1)-2{\mu }_{111}\{(1-R_i)Y_i(A_1{C}_1)\}+{\mu }_{111}^2|R_i,X_{1i}]]={\kappa }_1^2{P}_{1}E\left[\frac{X_{1i}}{P_1^2}E\right[R_i({\sigma }_{A_1{B}_1}^2+{\mu }_{A_1{B}_1}^2)-2{\mu }_{111}{R}_i{\mu }_{A_1{B}_1}+{\mu }_{111}^2|R_i,X_{1i}]]+{\kappa }_1^2{Q}_{1}E[\frac{X_{1i}}{Q_1^2}E[(1-R_i)({\sigma }_{A_1{C}_1}^2+{\mu }_{A_1{C}_1}^2)-2{\mu }_{111}(1-R_i){\mu }_{A_1{C}_1}+{\mu }_{111}^2|R_i,X_{1i}\left]\right]={\kappa }_1^{2}E\left[X_{1i}E\right[\frac{R_i}{P_1}\{{\sigma }_{A_1{B}_1}^2+{\mu }_{A_1{B}_1}^2-2{\mu }_{A_1{B}_1}{\mu }_{111}+{\mu }_{111}^2\}+\frac{(1-R_i)}{Q_1}\{{\sigma }_{A_1{C}_1}^2+{\mu }_{A_1{C}_1}^2-2{\mu }_{A_1{C}_1}{\mu }_{111}+{\mu }_{111}^2\}|X_{1i}]]={\kappa }_1^{2}E[X_{1i}\left[\frac{{\pi }_1}{P_1}\right\{{\sigma }_{A_1{B}_1}^2+{({\mu }_{111}-{\mu }_{A_1{B}_1})}^2\}+\frac{(1-{\pi }_1)}{Q_1}\{{\sigma }_{A_1{C}_1}^2+{({\mu }_{111}-{\mu }_{A_1{C}_1})}^2\left\}\right]]={\kappa }_1[\frac{{\pi }_1}{P_1}\{{\sigma }_{A_1{B}_1}^2+{({\mu }_{111}-{\mu }_{A_1{B}_1})}^2\}+\frac{(1-{\pi }_1)}{Q_1}\{{\sigma }_{A_1{C}_1}^2+{({\mu }_{111}-{\mu }_{A_1{C}_1})}^2\}].$$

Consequently, the asymptotic variance of μ̂₁₁₁ is given by,

$$\mathit{\text{var}}({\hat{\mu }}_{111}^{IPWN})=\frac{{\kappa }_1}{n}[\frac{{\pi }_1}{P_1}\{{\sigma }_{A_1{B}_1}^2+{({\mu }_{111}-{\mu }_{A_1{B}_1})}^2\}+\frac{(1-{\pi }_1)}{Q_1}\{{\sigma }_{A_1{C}_1}^2+{({\mu }_{111}-{\mu }_{A_1{C}_1})}^2\}]=\frac{{\sigma }_{111}^2}{n}.$$

Estimators that share the same first-stage treatment would be correlated as they use a common group of observations. Consider ${\hat{\mu }}_{111}^{IPWN}$ and ${\hat{\mu }}_{112}^{IPWN}$.

To derive the covariance between strategy means ${\hat{\mu }}_{111}^{IPWN}$ and ${\hat{\mu }}_{112}^{IPWN}$, we note that similar to $\sqrt{n}({\hat{\mu }}_{111}^{IPWN}-{\mu }_{111}),\sqrt{n}({\hat{\mu }}_{112}^{IPWN}-{\mu }_{112})$ is distributionally equivalent to $n^{-1/2}{\kappa }_1{\sum }_{i=1}^n{W}_{112i}(Y_i-{\mu }_{112})$. Therefore, the asymptotic covariance of $\sqrt{n}({\hat{\mu }}_{111}^{IPWN}-{\mu }_{111})$ and $\sqrt{n}({\hat{\mu }}_{112}^{IPWN}-{\mu }_{112})$ is given by,

$${\sigma }_{111,112}=\mathit{\text{cov}}({\psi }_{111i},{\psi }_{112i})=\mathit{\text{cov}}({\kappa }_1{W}_{111i}(Y_i-{\mu }_{111}),{\kappa }_1{W}_{112i}(Y_i-{\mu }_{112}))=E[{\kappa }_1^2{W}_{111i}{W}_{112i}(Y_i-{\mu }_{111})(Y_i-{\mu }_{112})].$$

Since $W_{111i}{W}_{112i}=\frac{R_i{Z}_{1i}{X}_{1i}}{P_1^2}$, we can further simplify the above as,

$${\sigma }_{111,112}=E[{\kappa }_1^2\frac{R_i{Z}_{1i}}{P_1^2}{X}_{1i}(Y_i-{\mu }_{111})(Y_i-{\mu }_{112})]=E\left\{E\right[{\kappa }_1^2\frac{R_i{Z}_{1i}}{P_1^2}{X}_{1i}(Y_i(A_1{B}_1)-{\mu }_{111})(Y_i(A_1{B}_1)-{\mu }_{112})|R_i,X_{1i},Y_i(A_1{B}_1)]\},\text{by consistency assumption},={\kappa }_1^{2}E[X_{1i}\frac{R_i}{P_1^2}(Y_i(A_1{B}_1)-{\mu }_{111})(Y_i(A_1{B}_1)-{\mu }_{112})E\{Z_{1i}|R_i,X_{1i},Y_i(A_1{B}_1)\}]={\kappa }_1^{2}E[X_{1i}\frac{R_i}{P_1}(Y_i(A_1{B}_1)-{\mu }_{111})(Y_i(A_1{B}_1)-{\mu }_{112})]={\kappa }_1^{2}EE[X_{1i}\frac{R_i}{P_1}(Y_i(A_1{B}_1)-{\mu }_{111})(Y_i(A_1{B}_1)-{\mu }_{112})|X_{1i},Y_i(A_1{B}_1)]={\kappa }_1^{2}E[X_{1i}\frac{{\pi }_i}{P_1}(Y_i(A_1{B}_1)-{\mu }_{111})(Y_i(A_1{B}_1)-{\mu }_{112})|X_{1i},Y_i(A_1{B}_1)]={\kappa }_1^2\frac{{\pi }_1}{P_1}E[X_{1i}(Y_i(A_1{B}_1)-{\mu }_{111})(Y_i(A_1{B}_1)-{\mu }_{112})]={\kappa }_1\frac{{\pi }_1}{P_1}[{\sigma }_{A_1{B}_1}^2+{\mu }_{A_1{B}_1}^2-{\mu }_{111}{\mu }_{A_1{B}_1}-{\mu }_{112}{\mu }_{A_1{B}_1}+{\mu }_{111}{\mu }_{112}]={\kappa }_1\frac{{\pi }_1}{P_1}[{\sigma }_{A_1{B}_1}^2+({\mu }_{A_1{B}_1}-{\mu }_{111})({\mu }_{A_1{B}_1}-{\mu }_{112})].$$

Since, from Equation (2), (μ_A1B1 − μ₁₁₁) = μ_A1B1 − π₁μ_A1B1 − (1 − π₁)μ_A1C1 = (1 − π₁)(μ_A1B1 − μ_A1C1) and (μ_A1B1 − μ₁₁₂) = (1 − π₁)(μ_A1B1 − μ_A1C2), it follows that asymptotic covariance of μ̂₁₁₁ and μ̂₁₁₂ is given by

$$\mathit{\text{cov}}({\hat{\mu }}_{111}^{IPWN},{\hat{\mu }}_{112}^{IPWN})=\frac{{\kappa }_1}{n}\frac{{\pi }_1}{P_1}[{\sigma }_{A_1{B}_1}^2+{(1-{\pi }_1)}^2({\mu }_{A_1{B}_1}-{\mu }_{A_1{C}_1})({\mu }_{A_1{B}_1}-{\mu }_{A_1{C}_2})].$$ (11)

A similar derivation could be employed to compute other covariances. Let Σ = var(ψ_i), where ψ_i is the vector of eight influence functions ψ_jkli, j, k, l = 1, 2, denote the variance-covariance matrix where Equation (7) and similar entities are used to form the diagonal elements and Equation (11) is used to form the off-diagonal entries, respectively.