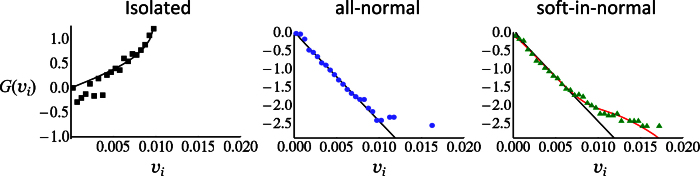
Figure 4. Velocity distribution of a tagged cell.

The probability distribution of the x or y component of the instantaneous velocity of the tagged cell when the cell (soft or normal) is isolated on the substrate (left panel), in the all-normal case (middle panel) and in the soft-in-normal case (right panel). The distribution functions have been scaled such that a Gaussian distribution gives a straight line. For the Gaussian case, 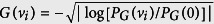. The markers show the simulation data. In the isolated case, the Black curve is the exact velocity distribution that arises from the active part of the velocity alone (see Eq. (4)). In the all-normal case, the velocity distribution of the tagged cell is well described by a Gaussian fit (Black line) with standard deviation σ_G = 0.0029. In the soft-in-normal case, the velocity distribution of the soft cancer cell is not well described by a Gaussian fit (Black line) with σ_G = 0.0028. It is better described by the distribution proposed in the main text, Eq. (5), which is shown here as the Red curve.