Variable selection in the presence of missing data: resampling and imputation

Abstract

In the presence of missing data, variable selection methods need to be tailored to missing data mechanisms and statistical approaches used for handling missing data. We focus on the mechanism of missing at random and variable selection methods that can be combined with imputation. We investigate a general resampling approach (BI-SS) that combines bootstrap imputation and stability selection, the latter of which was developed for fully observed data. The proposed approach is general and can be applied to a wide range of settings. Our extensive simulation studies demonstrate that the performance of BI-SS is the best or close to the best and is relatively insensitive to tuning parameter values in terms of variable selection, compared with several existing methods for both low-dimensional and high-dimensional problems. The proposed approach is further illustrated using two applications, one for a low-dimensional problem and the other for a high-dimensional problem.

1. Introduction

Variable selection has been extensively investigated for fully observed data and existing approaches include classical methods based on AIC (Akaike, 1974) and modern regularization methods such as lasso (Tibshirani, 1996). Compared with fully observed data, new challenges arise for variable selection in the presence of missing data. In particular, there are different missing data mechanisms and for each mechanism there are different statistical approaches for handling missing data. As a result, methods for variable selection need to be tailored to the missing data mechanism and the statistical approach used. Little and Rubin (2002) and Tsiatis (2006), together, provide a comprehensive review of existing statistical approaches for handling missing data. In the current paper, we focus on the mechanism of missing at random (MAR). Under MAR, variable selection has been investigated in combination with three commonly used statistical approaches for handling missing data.

The first approach for handling missing data includes inverse probability weighting (IPW) and its extensions including augmented IPW (AIPW); see Tsiatis (2006) and references therein. This approach has been combined with generalized estimation equations to handle missing data in semiparametric models. Johnson and others (2008) proposed a general approach of penalized estimating functions for variable selection and Wolfson (2011) proposed an EEBoost approach for variable selection based on estimating equations. Both can be applied to IPW and AIPW estimating equations for monotone missingness but are difficult to extend to general missing data patterns that are not monotone.

The second approach is to use likelihood-based methods; see Little and Rubin (2002, Section 8). One option for maximum likelihood estimation in this approach is to use the expectation-maximization (EM) algorithm. To conduct variable selection in this approach, Garcia and others (2009, 2010) proposed to incorporate SCAD and adaptive lasso penalties into the EM algorithm to maximize the penalized observed data likelihood function in the presence of missing data.

The third approach is to conduct imputation for missing values; cf. Little and Rubin (2002, Sections 4 and 5). Imputation methods can be conducted using existing software packages (Buuren and Groothuis-Oudshoorn, 2011; Raghunathan and others, 2001; Su and others, 2011) in a wide range of settings. When multiple imputation (MI) is used, it is natural and often not difficult to apply an existing variable selection method to each imputed data set, likely resulting in different sets of selected predictors from say 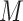imputed data sets. However, it is challenging to combine results on variable selection across 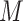imputed data sets in a principled framework. Heymans and others (2007), Wood and others (2008), and Lachenbruch (2011) investigated methods in which predictors are deemed important if they are selected in at least 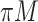imputed data sets (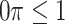). Heymans and others (2007) and Wood and others (2008) focused on classical methods, whereas Lachenbruch (2011) also considered the least angle regression (Efron and others, 2004). The difficulty with these methods is that variable selection results can be sensitive to the threshold value 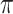and there is no clear guideline on how to choose 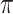. Alternatively, Yang and others (2005) proposed to combine MI with a Bayesian stochastic search variable selection (SSVS) procedure (George and McCulloch, 1997), either sequentially where Rubin's rule is used to combine variable selection results, or simultaneously where imputation is implemented—similar to a data augmentation step—as part of the MCMC algorithm that also includes an SSVS step. Chen and Wang (2013) proposed to treat the estimated regression coefficients of the same variable across all imputed datasets as a group and apply the group LASSO penalty for variable selection to the combined multiply imputed dataset.

In this paper, we investigate a variable selection method that can be combined with imputation; the method is applicable to general missing data patterns and to both low-dimensional and high-dimensional problems and draws strength from two seminal works, bootstrap imputation (Efron, 1994) and stability selection (Meinshausen and Buhlmann, 2010). Stability selection, a general subsampling/resampling approach for variable selection developed for fully observed data, entails the following steps: random subsampling or resampling of the observed data, then applying the randomized lasso to each random sample, and finally selecting important predictors based on the variable selection results from all random samples using a threshold 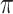. Stability selection has two notable strengths. First, variable selection results using stability selection are not very sensitive to the amount of regularization and the threshold value 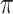. Second, and more importantly, Meinshausen and Buhlmann (2010) showed that stability selection with the randomized lasso is consistent in variable selection under a condition on the design that is considerably weaker than the irrepresentable condition that is (almost) necessary for the consistency of lasso. While originally proposed for fully observed data, the attractive features of stability selection make it an ideal variable selection procedure to be combined with bootstrap imputation.

Our proposed approach has several advantages compared with the existing methods. First, it can handle high-dimensional problems (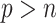), noting that all existing works only investigated low-dimensional problems (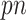) including their numerical studies. In particular, the methods proposed by Yang and others (2005) and Garcia and others (2009, 2010) all use a standard (unpenalized) regression model for imputing missing values, which is problematic for high-dimensional problems. Second, our approach can deal with general missing data patterns. It can be argued that the tools currently available to working biostatisticians make it considerably easier to conduct imputation for a general missing data pattern than a custom estimating equations-based or likelihood-based approach. Third, our approach avoids the well-known issues associated with IPW such as unstable weights, in particular when the number of complete cases is small. For comparison, we also consider combining bootstrap imputation with a bootstrapped lasso (Bolasso) approach proposed by Bach (2008). Bolasso is similar to stability selection in that it involves bootstrapping observed data and then applying lasso to each bootstrap sample. However, while Bolasso, similar to stability selection, achieves variable selection consistency when 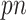under weaker conditions compared with the original lasso, it is very sensitive to the amount of regularization and its operating characteristics when 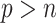are not fully understood (Bach, 2009).

2. Methodology

We consider a linear regression model for an outcome of interest, ,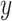

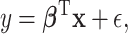(2.1)

where 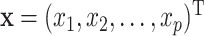is a set of 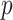predictors, 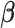is the vector of 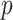regression coefficients, and 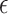is the random error term. Suppose that the data consist of 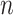observations and define 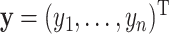and with 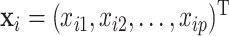, , 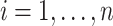where 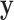is fully observed and 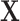has missing values. The missing data indicator matrix for 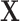is defined as 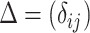such that 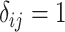if 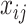is missing. Let 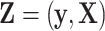denote the complete data, 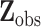denote the observed components of 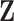, and 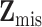denote the missing components. While we focus on variable selection for Model (2.1) in the presence of missing data in 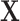, the proposed method can be readily extended to settings where 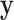also has missing values and to other types of regression analyses for which imputation is applicable. Throughout, we assume that data are MAR, i.e. 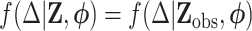, where 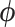denotes the set of parameters associated with the missing data mechanism 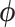and and 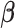are distinct, resulting in ignorable missingness. We denote by 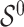the true active set in Model (2.1), that is, the set of variables for which the true regression coefficients are non-zero and by 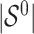the size (or cardinality) of .

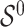2.1. Bootstrap imputation

We propose to first conduct bootstrap imputation on 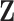in the spirit of Efron (1994) before variable selection. An outline of the bootstrap imputation procedure is as follows.

1. Generate 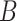bootstrap data sets 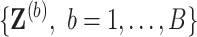with associated missing indicator matrix 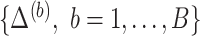based on the observed data and .

2. Conduct imputation for each bootstrap data set 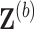and 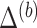using an imputation method of choice. The resultant imputed data sets are denoted by .

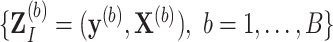Several remarks are in order. The bootstrap step is used because stability selection or Bolasso requires resampling of the observed data. When 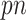, we can use standard imputation programs such as the R packages mi and mice or the stand-alone software IVEware (Raghunathan and others, 2001) to conduct a single imputation for each bootstrap sample; these software packages are applicable to general missing data patterns. When 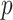is less than 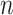but close to 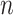, the existing software packages are applicable but may not perform well as shown in Zhao and Long (2013). When 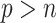, the existing software packages are not directly applicable. In such cases, model trimming or regularization is imperative when building imputation models; it is recommended by Zhao and Long (2013) that the Bayesian lasso regression or its extensions are preferred for imputing missing values since it has been shown to achieve better performance compared with several alternative imputation methods in the case of 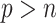. We follow this recommendation in our bootstrap imputation step for high-dimensional problems.

2.2. Stability selection combined with bootstrap imputation

Given the bootstrap imputed data sets 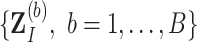, our proposed approach incorporates the strategy of stability selection within bootstrap imputation, which is referred to as BI-SS. An outline of the BI-SS approach is as follows.

1. Using the 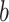th bootstrap imputed data set 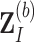, , 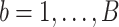we obtain the randomized lasso estimate 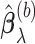for Model (2.1) as follows:

   

   where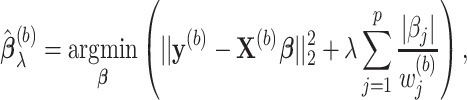 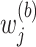's are independently identically distributed random variables in 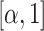with 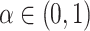. In practice, 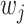's can be drawn from a uniform distribution or defined as 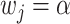with probability 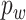and 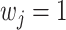with probability 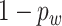; our numerical studies suggest that they perform similarly. In addition, 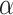can be chosen in the range of 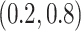following the recommendation by Meinshausen and Buhlmann (2010); in our numerical studies, we set 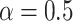. We compute 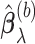for all 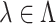, where 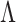denotes a set of feasible values for 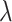. We denote by 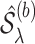the support of 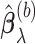(the set of non-zero parameter estimates), also known as the estimated active set.
2. We repeat Step (1) for all 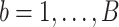bootstrap imputed data sets and obtain 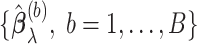. The final estimated active set is defined as

   

   where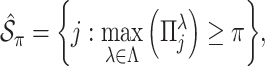 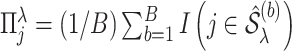and 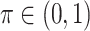is a threshold for selecting a predictor and is often set to between 0.6 and 0.9 in practice as suggested by Meinshausen and Buhlmann (2010). This threshold value is evaluated in our numerical studies.

3. While our focus is variable selection, we consider a straightforward approach for estimation of 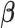. We fit Model (2.1) through least squares, 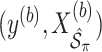to obtain 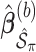, where 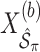denotes the design matrix that includes only the variables in 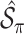, and then compute the final parameter estimates as 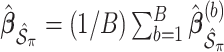. To estimate the variance of 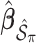, a naive approach is to use the sample variance of .

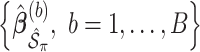BI-SS uses bootstrap samples rather than subsampling without replacement which is used in the original stability selection method (Meinshausen and Buhlmann, 2010). As noted in Meinshausen and Buhlmann (2010), bootstrap would behave similarly as their proposed subsampling approach. In the presence of missing data, the sharply reduced sample size in a random subsample, say, of size 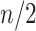, is expected to have major adverse effect on the performance of imputation given that we need to fit imputation models based on only observed data. As a result, we choose to use bootstrap over the original subsampling scheme.

2.3. Bolasso combined with bootstrap imputation

For comparison, we investigate another variable selection approach that incorporates lasso with bootstrap imputation, referred to as BI-BL, which is similar in spirit to Bolasso (Bach, 2008, 2009). This also mimics the approach for variable selection under MI using the bootstrap by Heymans and others (2007); of note, we use lasso for variable selection, which is preferred to the automatic backward selection used in Heymans and others (2007). An outline of the BI-BL procedure is as follows.

1. Using the 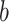th bootstrap imputed data set, 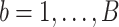, we obtain the lasso estimate 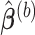for Model (2.1),

   

   where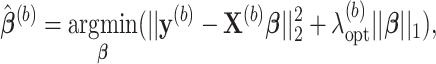 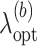is an optimal value of the tuning parameter selected based on cross-validation for each bootstrap imputed data set. We denote the support of 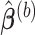by .
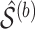2. We repeat the above step for all 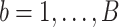bootstrap imputed data sets and then intersect all 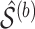s to obtain the final estimated active set,

   

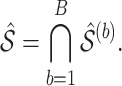
3. For estimation of 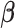, we adopt an approach similar to the one for BI-SS. We fit Model (2.1) through say, least squares, using 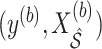to obtain 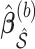, where 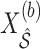denotes the design matrix including only the variables in 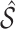, and then compute the final parameter estimates as .

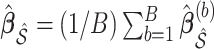As with the original Bolasso approach (Bach, 2008, 2009), we choose to use the intersection of the supports of the estimated active set across all bootstrap imputed data sets, which is justified by their asymptotic results for low-dimensional problems (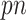). However, in finite samples, it is of interest to investigate the impact of different threshold values, similar to what is described in Section 2.2. Specifically, we compute , where 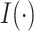is the indicator function. It follows that 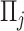represents the proportion of the bootstrap imputed data sets in which 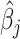is not zero. Subsequently, we define the final estimated active set as

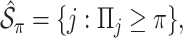where 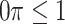is a pre-specified threshold value and 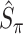with 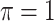is equivalent to 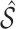, intersecting the supports of the estimated active sets across 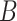bootstrap imputed data sets. Following Bach (2008), we investigate 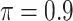in our numerical studies.

2.4. Outline of operating characteristics

Assuming that 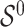is sparse (i.e. the support of 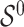is less than 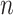and 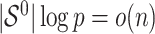) and the design 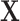satisfies the conditions as specified in Meinshausen and Buhlmann (2010), stability selection is shown to achieve consistent variable selection for model (2.1) using fully observed data, where 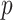is allowed to go to 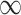as 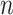goes to 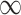. In addition, their method is not very sensitive to the tuning parameter 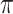in terms of variable selection. While theoretical results are not provided for the proposed BI-SS method, our simulation studies demonstrate that BI-SS achieves good performance in variable selection in a variety of settings for both low-dimensional and high-dimensional problems when the imputation model is correctly specified.

Using fully observed data, Bach (2008, 2009) showed in the case of 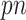that intersecting supports of lasso estimates from bootstrap imputed data sets 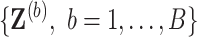(i.e. Bolasso) achieves consistent variable selection as 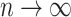. Bach (2009) noted that in the case of 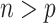Bolasso using the paired bootstrap procedure does not lead to good selection performance whereas Bolasso using a residual bootstrap procedure does; however, no theoretical results were provided for either approach in the case of 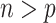. BI-BL, using the paired bootstrap approach, is shown in our numerical studies to achieve inferior performance. It is of future interest to adapt the residual bootstrap procedure in our setting where predictors have missing values. 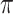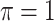In addition, variable selection results from Bolasso are quite sensitive to the tuning parameter and does not achieve good performance in finite samples, which is a major weakness of Bolasso and BI-BL.

3. Simulation studies

We evaluate in three sets of simulation studies the performance of the proposed approach BI-SS in comparison with BI-BL and other existing methods as appropriate. As mentioned before, BI-BL mimics the approach for variable selection under MI using the bootstrap by Heymans and others (2007). We consider different threshold values (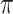) for BI-BL and BI-SS to assess their sensitivity to 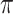. We summarize the simulation results over 1000 Monte Carlo (MC) data sets in the first two sets of simulations and 250 MC data sets in the third set of simulations. To evaluate performance in variable selection, we calculate the number of false negatives (FNs) (the number of predictors in the true active set 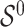that are not selected) and the number of false positives (FPs) (the number of noise predictors that are selected) for each MC data set and we report mean FN and FP. To evaluate prediction performance, we calculate the model error defined as 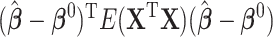for each MC data set and we report the median model error (MME).

3.1. Monotone missingness: comparison with penalized estimating functions

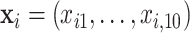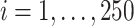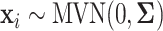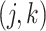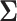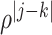In the first set of simulations, we compare the proposed method with BI-BL and the approach of penalized estimation functions (Johnson and others, 2008) and use a setup similar to what was used in Johnson and others (2008, Section 5.2). Specifically, , , is generated independently from a multivariate normal distribution, , where the th component of is with 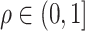. 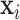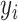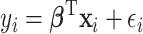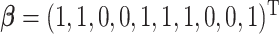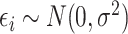Given , the outcome variable, , is generated from , where and is random noise and independent of 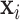. It follows that the true active set is 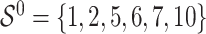and 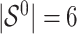. Missing data are generated using the same models described in Johnson and others (2008, Section 5.2), resulting in a monotone missing data pattern in 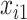and 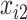and approximately 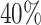of observations having missing values. For each MC data set, imputation is conducted using the R package mice on each of 100 bootstrap data sets in BI-BL and BI-SS. In addition, we apply the approach of penalized estimation functions with different penalties, namely, SCAD (PEF-S), hard thresholding (PEF-HT), lasso (PEF-L), adaptive lasso (PEF-AL), and elastic net (PEF-EN). We conduct simulations for different correlation among the predictors ( 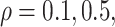and 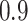) and for different levels of noise ( 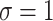and 2).

Table 1 summarizes the results from the first set of simulations. In all cases, the best performance achieved by BI-SS is similar to or slightly worse than the best results from the PEF methods. Similar to the results in Johnson and others (2008), there is no single best PEF method that outperforms the other PEF methods in all settings. The performance of BI-SS is similar when 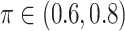, confirming that BI-SS is not very sensitive to different values of 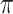in the recommended region. When correlation is low to moderate ( 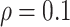or 0.5), BI-SS with 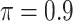leads to slightly lower MME and a lower sum of FN and FP than the other 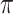values; when 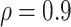BI-SS achieves best performance when 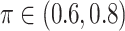. When correlation increases from 0.1 to 0.5, BI-SS achieves slightly better performance, likely due to the fact that there is limited information for imputation when 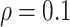. When correlation increases from 0.5 to 0.9, the comparisons are mixed, noting that high correlation (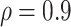) likely leads to better performance for imputation but it is also known to be associated with worse performance in variable selection. In all cases, BI-BL achieves worse performance than BI-SS and is fairly sensitive to the threshold value (), evidenced by a considerable increases in FP when 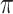decreases from 1 to 0.9. When correlation is low to moderate ( 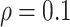or 0.5), BI-BL with a threshold of 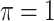leads to slightly better MME without sacrificing sensitivity. However, when correlation is high (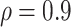), BI-BL with a threshold of 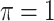tends to lead to worse MME, in particular when noise level is high (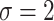). As the noise in the data (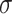) increases, the variable selection performance of all methods deteriorates.

Table 1.

Simulation results in the case of a monotone missing data pattern with 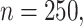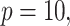and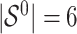

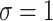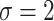	FN	FP	MME	FN	FP	MME
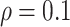BI-SS	0	0.853	0.083	0.008	0.917	0.290
BI-SS	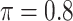0	1.098	0.088	0.005	1.156	0.303
BI-SS	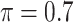0	1.373	0.090	0.003	1.398	0.315
BI-SS	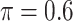0	1.637	0.093	0.003	1.677	0.326
BI-BL	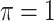0	1.300	0.087	0.005	1.251	0.302
BI-BL	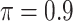0	2.405	0.100	0.002	2.312	0.342
PEF-S	0.016	1.119	0.065	0.081	0.728	0.341
PEF-HT	0.034	1.019	0.066	0.175	0.420	0.230
PEF-L	0.015	1.920	0.073	0.056	1.538	0.288
PEF-AL	0.013	0.460	0.067	0.065	0.498	0.296
PEF-EN	0.012	1.979	0.073	0.056	1.390	0.326
BI-SS	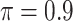0.004	0.435	0.072	0.080	0.577	0.259
BI-SS	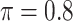0	0.752	0.080	0.034	0.917	0.279
BI-SS	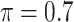0	1.065	0.085	0.017	1.223	0.294
BI-SS	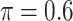0	1.400	0.087	0.007	1.540	0.305
BI-BL	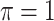0	1.063	0.086	0.022	0.922	0.284
BI-BL	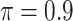0	2.105	0.098	0.008	1.960	0.332
PEF-S	0.063	0.899	0.075	0.222	0.760	0.330
PEF-HT	0.097	0.768	0.076	0.386	0.323	0.275
PEF-L	0.045	1.799	0.081	0.142	1.514	0.304
PEF-AL	0.055	0.525	0.076	0.181	0.607	0.331
PEF-EN	0.045	1.858	0.083	0.159	1.438	0.332
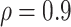BI-SS	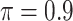1.206	0.021	0.222	2.071	0.223	0.501
BI-SS	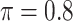0.170	0.252	0.066	1.002	0.656	0.304
BI-SS	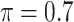0.036	0.694	0.069	0.609	1.007	0.262
BI-SS	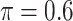0.014	1.157	0.070	0.391	1.350	0.250
BI-BL	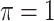0.067	0.901	0.073	1.139	0.782	0.347
BI-BL	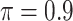0.024	2.005	0.087	0.584	1.767	0.321
PEF-S	0.358	0.705	0.078	1.536	0.880	0.449
PEF-HT	0.224	1.165	0.085	1.198	1.121	0.400
PEF-L	0.135	1.732	0.083	0.382	1.963	0.282
PEF-AL	0.318	0.709	0.098	1.207	0.946	0.394
PEF-EN	0.142	1.813	0.083	0.402	1.932	0.286

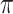is the threshold value.

FN, average number of false negatives; FP, average number of false positives; MME, median model error; BI-SS, bootstrap imputation combined with stability selection; BI-BL, bootstrap imputation combined with Bolasso; PEF-S, penalized estimating functions with SCAD; PEF-HT, penalized estimating functions with hard thresholding; PEF-L, penalized estimating functions with Lasso; PEF-AL, penalized estimating functions with adaptive Lasso; PEF-EN, penalized estimating functions with elastic net.

3.2. General missing data pattern

In the second set of simulations, we investigate a general missing data pattern and a larger number of predictors (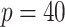) compared with the first set of simulations. In the presence of a general missing data pattern, it is challenging to derive inverse weighted estimating functions. Furthermore, a general missing data pattern often results in a small number of complete cases and consequently unstable parameter estimates when estimating functions with inverse weighting are used. As a result, the PEF approach is not directly applicable or suitable in this set of simulations. We compare BI-SS with four other methods, namely, BI-BL, one naive method denoted by Lasso which applies lasso to the subset of complete cases, MI-Lasso which applies lasso to each of 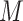multiply imputed data set and defines the estimated active set as the set of variables that are selected from 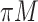imputed data sets, and MI-Stacked which applies lasso to one large data set that stacks the 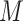imputed data sets together. MI-Lasso is the same as a method investigated by Lachenbruch (2011) and similar to the method S2 in Wood and others (2008), in both of which 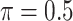is used. MI-Stacked is similar to the method W1 used in Wood and others (2008) with the stepwise procedure replaced by lasso.

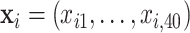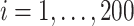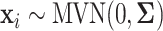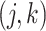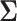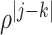In this set of simulations, , , is generated independently from , where the th component of is with 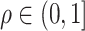. The outcome variable, 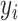, is generated from 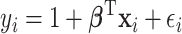, where 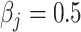or 1 if 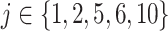representing the effect size (ES) and 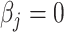if otherwise, and 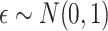is random noise and independent of 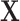. It follows that the true active set is 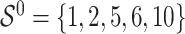and its size is 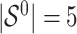. 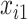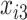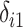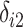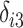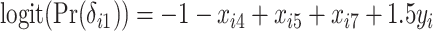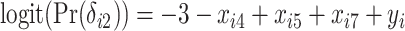Missing values are generated in , , and using the following models for the corresponding missing indicators, , , and , , , and 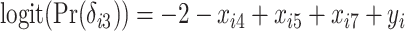, resulting in a general missing data pattern and approximately 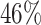of observations having missing values. For each MC data set, imputation is conducted using the R package mice on each of 100 bootstrap data sets in BI-BL and BI-SS. Similar to Section 3.1, we conduct simulations for different correlation among the predictors and for different ESs as measured by the value of non-zero 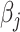, 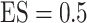or 1.

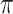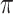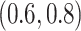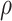Table 2 summarizes the results in the second set of simulations. When comparing performance between BI-BL and BI-SS and between different , the results in Table 2 are consistent to what are observed in Table 1. In particular, BI-SS outperforms BI-BL in all cases and leads to small to negligible FN and FP. BI-SS again achieves similar performance in variable selection as varies in . As increases from 0 to 0.5, its performance improves; as 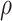increases from 0.5 to 0.9, its performance in variable selection deteriorates and the comparisons in terms of MME are mixed. When correlation is close to 0, BI-SS with a lower 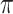value achieves best performance; as correlation increases, BI-SS with a lower 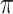value achieves better performance. BI-BL has substantially higher FP as 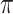decreases from 1 to 0.9. The impact of 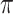on BI-BL is even more pronounced in this setting; e.g. as 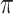decreases from 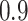to 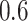in the case of 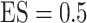and 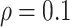, FP increases from 11.963 to 24.219 for BI-BL but only from 0.465 to 2.185 for BI-SS. In addition, Lasso, MI-Lasso, and MI-Stacked all have considerably to substantially worse performance compared with BI-SS particularly in terms of FP. As the ES increases, FN decreases and MME increases for all methods.

Table 2.

Simulation results in the case of a general missing data pattern with 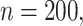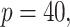and 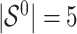for different ESs

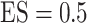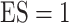	FN	FP	MME	FN	FP	MME
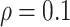BI-SS	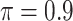0.220	0.465	0.084	0.006	0.304	0.126
BI-SS	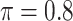0.119	0.890	0.098	0.003	0.668	0.150
BI-SS	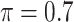0.070	1.447	0.119	0.002	1.116	0.175
BI-SS	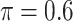0.045	2.185	0.143	0.001	1.709	0.204
Lasso	0.104	10.715	0.356	0	12.336	0.576
BI-BL	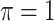0.106	3.973	0.174	0.002	7.336	0.301
BI-BL	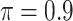0.027	11.963	0.306	0.002	20.091	0.584
MI-Lasso	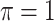0.005	7.963	0.186	0.000	15.950	0.449
MI-Lasso	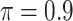0.003	10.396	0.219	0.000	19.095	0.493
MI-Lasso	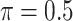0.002	13.258	0.252	0.000	22.079	0.525
MI-Stacked	0.000	34.803	0.360	0.000	34.935	0.602
BI-SS	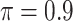0.287	0.449	0.078	0.014	0.304	0.112
BI-SS	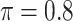0.162	0.880	0.089	0.005	0.629	0.129
BI-SS	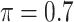0.086	1.447	0.105	0.002	1.084	0.152
BI-SS	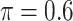0.054	2.130	0.123	0.002	1.696	0.172
Lasso	0.088	9.161	0.349	0	9.891	0.566
BI-BL	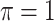0.273	3.370	0.186	0.014	6.395	0.251
BI-BL	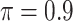0.091	10.957	0.290	0.002	18.730	0.524
MI-Lasso	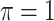0.008	6.214	0.151	0.000	13.319	0.391
MI-Lasso	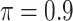0.006	8.429	0.177	0.000	16.464	0.440
MI-Lasso	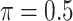0.003	11.352	0.211	0.000	19.999	0.493
MI-Stacked	0.000	34.845	0.356	0.000	34.898	0.599
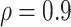BI-SS	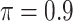2.907	0.220	0.318	1.598	0.173	0.528
BI-SS	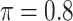1.901	0.560	0.153	0.576	0.454	0.167
BI-SS	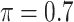1.252	1.065	0.100	0.245	0.895	0.120
BI-SS	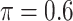0.785	1.809	0.089	0.099	1.587	0.121
Lasso	0.620	5.883	0.335	0.024	6.466	0.411
BI-BL	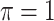2.315	1.911	0.245	0.892	4.497	0.325
BI-BL	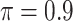1.197	8.229	0.233	0.247	15.995	0.454
MI-Lasso	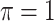0.332	3.635	0.079	0.030	7.531	0.178
MI-Lasso	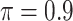0.282	5.155	0.094	0.019	10.990	0.250
MI-Lasso	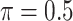0.240	7.649	0.120	0.015	15.189	0.324
MI-Stacked	0.005	34.825	0.326	0.001	34.869	0.512

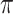is the threshold value.

FN, average number of false negatives; FP, average number of false positives; MME, median model error; BI-SS, bootstrap imputation combined with stability selection; Lasso, applying lasso to the subset of complete cases; BI-BL, bootstrap imputation combined with Bolasso; MI-Lasso, applying lasso to each of 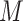multiply imputed data set and defining the active set as the set of variables that are selected from 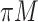imputed data sets; MI-stacked, applying lasso to one large data set that stacks the 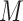imputed data sets together.

3.3. High-dimensional setting

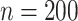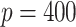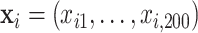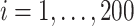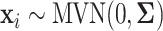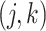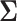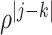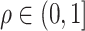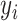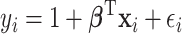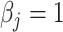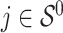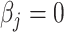In the third set of simulations, we investigate the case of high-dimensional data ( and ). In this setting, the PEF methods are not directly applicable. Similar to previous two settings, , , is generated independently from , where the th component of is with . The outcome variable, , is generated from , where or 0.5 for and if otherwise and 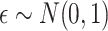is random noise and independent of 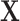. The true active set is 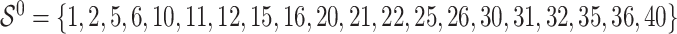with . 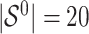Missing values are generated in 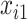using the following model for the corresponding missing indicator, 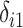, , 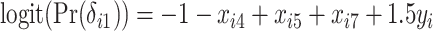resulting in approximately 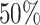of observations having missing 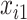. For each MC data set, imputation is conducted using the Bayesian lasso imputation approach proposed by Zhao and Long (2013) on each of 100 bootstrap data sets. Similar to Section 3.2, we compare BI-SS with the naive approach Lasso and two existing methods MI-Lasso and MI-Stacked for different correlation among the predictors and for different ESs. BI-BL is not included since BoLasso is not expected to perform well in this setting (Bach, 2009).

The simulation results are summarized in Table 3. In this setting, BI-SS with 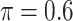gives similar or better results compared with the other threshold values, in particular, in terms of the sum of FN and FP. BI-SS with 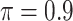, in some cases 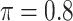and 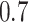as well, leads to a substantially larger MME and higher number of FNs compared with smaller threshold values, in particular when 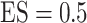, whereas BI-SS with 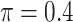, in some cases 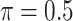as well, selects considerably more FPs. It follows that BI-SS is more sensitive to 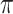for high-dimensional problems particularly in terms of MME and BI-SS with 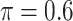is likely preferred in similar high-dimensional problems. As 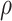increases, MME improves for BI-SS with 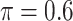, likely the result of improved imputation; though its performance in variable selection deteriorates. In addition, similar to the simulation results for low-dimensional problems in Section 3.2, Lasso and MI-Lasso select a large number of predictors, most of which are FPs.

Table 3.

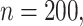
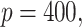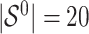Simulation results in the case of high-dimensional data with and for different ESs

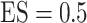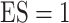	FN	FP	MME	FN	FP	MME
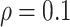BI-SS	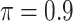13.548	0.000	3.848	8.524	0.000	9.619
BI-SS	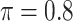9.536	0.052	2.724	4.840	0.020	5.682
BI-SS	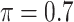6.724	0.232	2.036	3.060	0.164	3.572
BI-SS	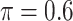4.644	0.732	1.513	2.064	0.520	2.513
BI-SS	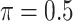3.180	2.076	1.185	1.392	1.416	1.692
BI-SS	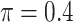2.052	4.980	1.037	0.864	3.676	1.606
Lasso	11.132	32.112	4.676	13.524	24.436	20.423
MI-Lasso	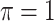0.924	33.052	1.215	0.512	23.456	1.978
MI-Lasso	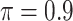0.540	50.948	1.343	0.064	45.984	2.254
MI-Lasso	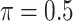0.120	69.140	1.474	0.000	72.736	2.636
BI-SS	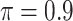8.144	0.028	2.119	2.432	0.016	2.004
BI-SS	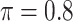4.600	0.132	1.157	1.312	0.096	1.153
BI-SS	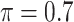2.704	0.460	0.809	0.976	0.308	1.133
BI-SS	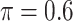1.664	1.056	0.608	0.732	0.832	1.134
BI-SS	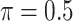1.124	2.388	0.576	0.536	1.956	1.168
BI-SS	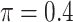0.680	5.120	0.612	0.332	4.152	1.241
Lasso	4.884	49.248	3.965	4.872	51.048	16.220
MI-Lasso	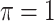0.832	28.048	0.991	0.328	19.396	1.336
MI-Lasso	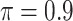0.368	43.608	1.106	0.048	38.408	1.664
MI-Lasso	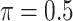0.072	60.164	1.220	0.000	46.592	2.052
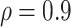BI-SS	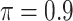17.776	0.004	13.227	11.356	0.004	6.297
BI-SS	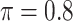12.376	0.100	2.002	4.224	0.048	1.147
BI-SS	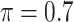7.452	0.668	0.620	1.272	0.476	0.549
BI-SS	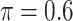3.600	2.060	0.401	0.412	1.988	0.488
BI-SS	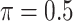1.412	4.732	0.363	0.092	5.040	0.526
BI-SS	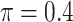0.496	9.304	0.407	0.012	10.576	0.609
Lasso	3.628	37.672	1.244	0.604	41.864	1.640
MI-Lasso	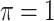2.136	24.268	0.663	0.488	21.676	0.816
MI-Lasso	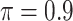1.256	36.200	0.761	0.072	38.044	1.030
MI-Lasso	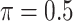0.700	48.460	0.873	0.008	58.528	1.229

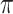is the threshold value.

FN, average number of false negatives; FP, average number of false positives; MME, median model error; BI-SS, bootstrap imputation combined with stability selection; Lasso, applying lasso to the subset of complete cases; MI-Lasso, applying lasso to each of 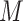multiply imputed data set and defining the active set as the set of variables that are selected from 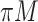imputed data sets.

4. Data examples

We conduct two data analyses, one for the case of low-dimensional data and the other for the case of high-dimensional data.

4.1. Stroke registry data

We first analyze a data set from the pilot Paul Coverdell National Acute Stroke Registry. This registry collects demographic, quantitative, and qualitative factors related to acute stroke care in four prototype states: Georgia, Massachusetts, Michigan, and Ohio. Its primary goal is to improve the quality of acute stroke care in the United States through a better understanding of factors associated with stroke. The Georgia prototype registry contains a sample of 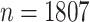patients with hemorrhagic or ischemic stroke and missing data are present with a general missing data pattern. Previously, Johnson and others (2008) selected a subset of 800 patients for their analysis to ensure a monotone missing data pattern so that their methods were directly applicable. Using our proposed approaches based on bootstrap imputation, we are able to analyze the entire sample of 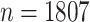patients.

The data set has 13 variables including a hospital length of stay (LOS), defined as the number of days from hospital admission to hospital discharge, which is considered as the outcome variable of interest in our analysis. The other variables are considered predictors of interest including age, gender (1 if male), race (1 if white), serum albumin, creatinine, glucose, Glasgow coma scale (GCS; 3–15, with 15 representing excellent health), whether or not the patient was admitted to the intensive care unit (ICU; 1 if yes), stroke subtype (stroke; 1 if hemorrhagic and 0 if ischemic), family history (FH; 1 if yes), use of EMS (EMS; 1 if yes), and admitted to emergency room (ER; 1 if yes). Only three variables (EMS, ER, and stroke) are fully observed; the amount of missing data in the other variables ranges between 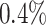in gender to 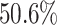in albumin. Only 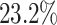of the patients are complete cases that have observed data for all variables. Similar to Johnson and others (2008), we find that the missing data mechanism in the full data is unlikely to be missing completely at random. Similar to the simulation studies, we apply five methods to the data set, namely, the proposed BI-SS (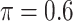), BI-BL (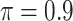), Lasso, MI-Lasso (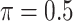), and a naive full model that is applied to the set of complete cases and does not do variable selection. Of note, 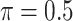is used for MI-Lasso following Lachenbruch (2011). For BI-BL and BI-SS, 1000 bootstrap data sets are generated and the R package mice is used for imputation. We only provide SEs for the naive full model.

Table 4 presents the results of our analyses. Compared with the naive full model, both BI-SS and BI-BL drops EMS, and BI-BL drops five additional predictors, including gender, FH, ER, stroke, and creatinine; in addition, the estimated effect of gender using BI-SS is opposite of the estimated effect using the naive full model. When 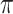is changed from 0.6 to 0.8, BI-SS drops only one additional predictor, ER; however, when 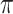is changed from 0.9 to 1.0, BI-BL drops four additional predictors, GCS, glucose, albumin, and age, again showing that BI-BL is substantially more sensitive to 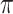than BI-SS. When using only complete cases, Lasso selects eight predictors excluding gender, FH, EMS, and ER and MI-Lasso selects the same set of predictors as BI-SS except for ER.

Table 4.

Regression coefficient estimates for the stroke data

	Full	Lasso	MI-Lasso	BI-BL	BI-SS
			()	()	()
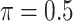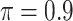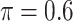Gender	-0.253	0	0.514	0	0.542
FH	0.692	0	0.515	0	0.505
ICU	4.114	3.935	3.333	3.655	3.362
EMS	-1.604	0	0	0	0
ER	3.150	0	0	0	1.202
Stroke	1.710	1.553	1.467	0	1.453
Race	-3.014	-2.928	-1.927	-1.933	-1.940
GCS	-0.197	-0.178	-0.233	-0.268	-0.244
Creatinine	-0.457	-0.506	-0.126	0	-0.131
Glucose	-0.004	-0.004	-0.001	-0.001	-0.001
Albumin	-1.775	-1.813	-1.531	-1.382	-1.549
Age	-0.045	-0.047	-0.007	-0.011	-0.007

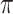is the threshold value.

Full, a full model applied to the subset of complete cases; Lasso, lasso applied to the subset of complete cases; MI-Lasso, MI combined with lasso; BI-BL, bootstrap imputation combined with Bolasso; BI-SS, bootstrap imputation combined with stability selection.

There are some differences between our results and the results in Johnson and others (2008), likely a consequence of using more data and more variables in our analysis. Specifically, while our BI-SS approach selects both gender and glucose, gender was not selected by any PEF method and glucose was only selected by PEF-lasso and PEF-EN in Johnson and others (2008). For predictors selected by both our methods and the PEF methods, their effects estimated using our methods are consistent with those in Johnson and others (2008), though the effect of age in our analysis is considerably smaller. For predictors that were not analyzed by Johnson and others (2008), BI-SS shows that FH and ER are associated with longer LOS.

4.2. Prostate cancer data

The second data set is from a prostate cancer study (GEO GDS3289). It contains 104 samples, including 34 benign epithelium samples and 70 non-benign samples. Missing values are present for some genomic biomarkers. To illustrate the methods, we consider a binary outcome (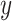) defined as 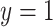if it is a benign sample and 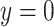if otherwise and we choose a subset of biomarkers for our analysis. Specifically, we choose one biomarker (EFCAB6) that has about 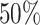missing values and use all of the 1894 biomarkers that do not have any missing values. Our goal is to conduct variable selection in a logistic regression of 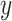on the set of 1000 biomarkers. Similar to Section 4.1, we apply four methods to the prostate cancer data except for the naive full model which is no longer applicable. For BI-BL and BI-SS, 1000 bootstrap data sets are generated and the Bayesian lasso imputation approach suggested by Zhao and Long (2013) is used for imputation. In addition, Step 1 as described in Sections 2.2 and 2.3 is adapted to fit penalized logistic regression in this data analysis.

Table 5 presents the results on variable selection for the prostate cancer data. Based on our simulation results, both Lasso and MI-Lasso tend to select a large number of FPs with low specificity, which seems to be consistent with the patterns in Table 2 with Lasso and MI-Lasso selecting 14 and 17 genomic biomarkers, respectively. By comparison, BI-SS (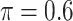) selects 5 gene biomarkers, of which 3 are also selected by both Lasso and MI-Lasso. EFCAB6 that has missing values is selected by BI-SS but not by the other methods, possibly suggesting that BI-SS is more likely to identify important predictors that have missing values. For BI-SS, 2 predictors are dropped when 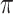increases to 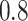, which is consistent with our simulations results in Section 3.3. BI-BL (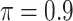) selects only one biomarker, noting that the validity of the bootstrap lasso investigated in this work is questionable for high-dimensional problems (Bach, 2009).

Table 5.

Results on variable selection for the prostate cancer data

Method	Selected biomarkers
Lasso	CPS1, MME, SOX4, AMACR, MYO6, ADAMTS1, SLC14A1, ENG,
	CLDN4, GREM1, IMAGE:141854, PTPRF, ACSS3, CCK
MI-Lasso (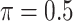)	ATP8A1, IMAGE:40728, IMAGE:470914, CPS1,
	MME, UBE2M, SOX4, MMP7, AMACR, MYO6, IMAGE:782760,
	ENG,CLDN4, IMAGE:141854, ITM2A, ACSS3, CCK
BI-BL (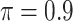)	AMACR (0.986)
BI-SS (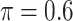)	EFCAB6 (0.84), MME (0.845), AMACR (0.968),
	IMAGE:141854 (0.790), ITM2A(0.715)

The number inside parentheses represents the proportion of being selected in 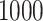bootstrap imputations. 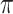is the threshold value.

Lasso, lasso applied to the subset of complete cases; MI-Lasso, MI combined with lasso; BI-BL, bootstrap imputation combined with Bolasso; BI-SS, bootstrap imputation combined with stability selection.

5. Discussion

We investigate a general resampling approach for variable selection in the presence of missing data. Our numerical results show that BI-SS with 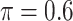achieves good performance for both low-dimensional and high-dimensional problems. While we focus on regression analysis, the proposed approach can be readily applied to other types of analyses such as graphical modeling. Attaching standard errors to parameter estimates in the setting of our interest is a challenging task. One approach is to apply existing methods for obtaining standard errors to the original data restricted to the predictors chosen by the variable selection process, similar to the naive approach in Section 2.2. However, this approach fails to account for the uncertainty of variable selection and hence likely understates the true sampling variance. Future research in this direction may include extending the work of Chatterjee and Lahiri (2011).

In order for BI-SS to achieve good performance, adequate imputation methods are needed and imputation models need to be carefully constructed, which is substantially more challenging in the presence of high-dimensional data. Particularly, while Zhao and Long (2013) suggested some ideas on imputation for general missing data patterns in the case of 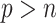, such imputation methods have not been fully developed and validated. Further research in this direction is an ongoing interest of ours but beyond the scope of the current paper.

Funding

This work was supported in part by a PCORI award (ME-1303-5840) and NIH/NCI grants (CA173770 and CA183006). The content is solely the responsibility of the authors and does not necessarily represent the official views of the PCORI or the NIH.