Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Jan 1.
Published in final edited form as: Magn Reson Imaging. 2016 Aug 29;35:154–159. doi: 10.1016/j.mri.2016.08.020

On the influence of zero-padding on the nonlinear operations in Quantitative Susceptibility Mapping

Sarah Eskreis-Winkler a, Dong Zhou a, Tian Liu b, Ajay Gupta a, Susan A Gauthier c, Yi Wang a, Pascal Spincemaille a
PMCID: PMC5160043  NIHMSID: NIHMS814040  PMID: 27587225

Abstract

Purpose

Zero padding is a well-studied interpolation technique that improves image visualization without increasing image resolution. This interpolation is often performed as a last step before images are displayed on clinical workstations. Here, we seek to demonstrate the importance of zero padding before rather than after performing non-linear post-processing algorithms, such as Quantitative Susceptibility Mapping (QSM). To do so, we evaluate apparent spatial resolution, relative error and depiction of multiple sclerosis (MS) lesions on images that were zero padded prior to, in the middle of, and after the application of the QSM algorithm.

Materials and Methods

High resolution gradient echo (GRE) data were acquired on twenty MS patients, from which low resolution data were derived using k-space cropping. Pre-, mid-, and post-zero padded QSM images were reconstructed from these low resolution data by zero padding prior to field mapping, after field mapping, and after susceptibility mapping, respectively. Using high resolution QSM as the gold standard, apparent spatial resolution, relative error, and image quality of the pre-, mid-, and post-zero padded QSM images were measured and compared.

Results

Both the accuracy and apparent spatial resolution of the pre-zero padded QSM was higher than that of mid-zero padded QSM (p < 0.001; p < 0.001), which was higher than that of post-zero padded QSM (p < 0.001; p < 0.001). The image quality of pre-zero padded reconstructions was higher than that of mid- and post-zero padded reconstructions (p = 0.004; p < 0.001).

Conclusion

Zero padding of the complex GRE data prior to nonlinear susceptibility mapping improves image accuracy and apparent resolution compared to zero padding afterwards. It also provides better delineation of MS lesion geometry, which may improve lesion subclassification and disease monitoring in MS patients.

Keywords: Quantitative Susceptibility Mapping (QSM), Microstructure, Zero padding, Nonlinearity, Multiple Sclerosis

1.1 INTRODUCTION

Quantitative susceptibility mapping (QSM) is a recently developed contrast technique that depicts and quantifies magnetic sources in the body, such as iron, deoxyhemoglobin, calcium, and contrast agents (1, 2). Several clinical applications of QSM, such as visualization of multiple sclerosis (MS) lesion geometry, require high spatial resolution.

In current practice, reconstructing high spatial resolution QSM necessitates 1) a longer scan time to acquire high resolution MRI data, and 2) deconvolution using a high resolution dipole kernel, which reduces the discretization error. This is because in previous work, magnetic susceptibility maps are solved at the same resolution as the acquired MRI data (1, 3–5).

To avoid lengthening scan time, this paper explores the utility of zero padding the complex gradient echo (GRE) data prior to performing susceptibility mapping. Zero padding is a well-studied interpolation technique that improves image visualization without increasing image resolution (6–12). It is generally applied as a final step before images are displayed on clinical workstations. Here we seek to demonstrate that when there are non-linear post-processing steps, such as QSM, it is important to zero pad prior to rather than after performing the QSM algorithm. The major nonlinear steps within QSM using MEDIN (13) are temporal and spatial phase unwrapping, nonlinear field map fitting and L1 regularized dipole field fitting.

In this paper, we demonstrate that zero padding of the complex GRE data prior to, rather than following, nonlinear QSM results in a susceptibility map with increased apparent spatial resolution, decreased relative error, and improved depiction of MS lesions as compared to post-zero padding (i.e., zero padding of the susceptibility map reconstructed directly from low resolution data using a low resolution dipole kernel). Additionally, we explore the effect of zero padding at various stages of the QSM algorithm. Since the QSM algorithm is non-linear, the zero padding operation and the QSM algorithm are not commutative; it is therefore instructive to explore at which point it is best to perform the zero padding operation.

1.2 MATERIALS AND METHODS

Low resolution complex GRE data were simulated by cropping the k-space of the high resolution data. Pre-, mid- and post-zero padded QSM images were reconstructed from these low resolution data using a zero padding step at the beginning, middle, and end of the QSM algorithm respectively (see below for details). These reconstructions were compared using high resolution QSM, obtained from the original high resolution data, as the gold standard.

To further evaluate the k-space effects of zero padding before versus after non-linear operations, the k-space of field maps derived from pre- and post-zero padded low resolution complex GRE data were compared to the k-space of the field map derived from high resolution complex GRE data.

1.2.1 Data Acquisition

Healthy subject

A multi-echo 3D gradient echo scan was acquired using a single-channel head coil on a 3T scanner (GE Healthcare, Waukesha, WI) in accordance with our Insitutional Review Board (IRB) (matrix size: 240×194×60, voxel size: 0.9375×0.9375×2mm3, 11 echoes, TE1/ΔTE/TR: 4.5/4.8ms, flip angle 20 degrees, bandwidth 62.5 kHz).

Multiple sclerosis patients

This retrospective study was approved by our IRB. We reviewed the MRI database in our institution’s clinical imaging database and identified 20 patients who met both of the following criteria: a) clinically confirmed MS patients; b) underwent an MR scan including a 3D multiple-echo GRE sequence using a 8-channel head coil (matrix size: 512×512×50, voxel size: 0.47×0.47×3mm, 11 echoes, TE1/ΔTE/TR: 4.5/4.8/57.9ms, flip angle 20 degrees, bandwidth 62.5 kHz) as part of the current standard-of-care at our institution during October 2013. MRI was performed on a 3T scanner (GE Healthcare, Waukesha, WI). All 20 patients (6 male, 14 female, aged 32 – 69, 46 ± 10 years) had expanded disability status scale ranging from 0 to 8 (median: 1.25) and disease duration ranging from 3 to 26 (11 ± 7) years. All patients were treated with a standard FDA immunomodulatory therapy.

1.2.2 Post-processing

For the healthy subject and the MS patients, low resolution scans were simulated by discarding the outer half of the complex k-space in all three dimensions.

To reconstruct QSM images, phase images were temporally unwrapped, a field map was generated by performing a voxel-by-voxel non-linear least squares fitting of the complex signal over TE, and the resultant field map was spatially unwrapped. Next, the background field, defined as the magnetic field generated by susceptibility sources outside the region of interest (ROI), was removed by applying Projection onto Dipole Fields (PDF) (14), obtaining the local field. The ROI was set to the brain as obtained by the BET segmentation algorithm (15). Using the local field, the magnetic field-to-susceptibility-source inverse problem was solved using morphology enabled dipole inversion (MEDI), which uses an L1 regularization term to promote similarity of edges between the QSM solution and the GRE magnitude image (13, 16–18).

For each subject, the following QSM reconstructions were performed:

  1. High resolution QSM: The unmodified high resolution complex GRE data were used to generate a “gold standard” QSM.

  2. Pre-zero padded low resolution QSM: Low resolution complex GRE data were zero padded to achieve a matrix size equivalent to that of the high resolution data, followed by QSM.

  3. Mid-zero padded low resolution QSM: Low resolution complex GRE data were used to generate a low resolution local field map using the same methods described above. This field map was then zero padded, followed by dipole inversion using MEDI.

  4. Post-zero padded low resolution QSM: Low resolution complex GRE data were used to generate a QSM image, as described above, followed by zero-padding to achieve a matrix size equivalent to that of the high resolution data.

All QSM images therefore had the same matrix size, which was 8 times that of the low resolution QSM image before zero padding. To avoid display interpolation issues, only QSM images of the same size, as described in the above, were considered for comparison.

1.2.3 K-space field map post-processing

For the healthy subject, k-space of the following field maps were reconstructed:

  1. High resolution field map: The unmodified high resolution complex GRE data were used to generate a “gold standard” field map

  2. Pre-zero padded low resolution field map: Low resolution complex GRE data were zero padded to achieve a matrix size equivalent to that of the high resolution data, followed by field map estimation.

  3. Post-zero padded low resolution field map: Low resolution complex GRE data were used to generate a field map followed by zero-padding to achieve a matrix size equivalent to that of the high resolution data.

1.2.4 Image Analysis

1.2.4.1 Image quality score

For each MS patient, a neuroradiologist with 8 years of experience identified the three largest lesions on T2W that were also visible on the high resolution QSM reconstruction. For each lesion, the neuroradiologist blindly assigned image quality scores to the pre-, mid- and post-zero padded QSM images using the following scale: 0: lesion was not visible; 1: the lesion was either poorly visible or differed markedly from the appearance on high resolution QSM; 2: lesion visibility was fair and generally resembled that of the high resolution QSM; 3: the lesion was well visualized and there was good geometrical agreement with the high resolution QSM. A Wilcoxon rank sum test was performed to test for statistically significant differences in image quality.

1.2.4.2 Apparent spatial resolution

For the healthy subject as well as for the MS patients, apparent spatial resolution was calculated for each reconstruction method by computing the point spread function (PSF) of the pre-, mid-, and post-zero padded QSM images with respect to the high resolution QSM:

k=argmink‖QSMZP−k∗QSMHR‖2

where ∗ denotes convolution, k is the PSF, and QSMHR and QSMZP denotes the high resolution and the zero-padded QSM image, respectively. This minimization was solved by deconvolving the reconstructed QSM image with the high resolution QSM by division in Fourier space. The resulting three-dimensional point spread function was plotted and the full-width-half-maximum (FWHM) of the point spread function (PSF) in each dimension was computed as a measure of apparent image resolution.

PSFs were calculated for the healthy subject, and for each MS patient. A paired t-test with Bonferroni correction was performed over the FWHM of the PSF in all MS patients to test for statistically significant differences in apparent spatial resolution.

1.2.4.3 Image accuracy

For the healthy subject as well as for the MS patients, the relative error of the pre-, mid- and post-zero padded QSM methods were calculated over the whole image by computing:

E=‖QSMHR−QSMZP‖‖QSMHR‖.

These calculations were repeated on rectangular ROIs circumscribing each of the MS lesions identified by the neuroradiologist. A paired t-test with Bonferroni correction over all lesion ROIs was performed to compare the relative errors for the pre-zero padded, mid-zero padded and post-zero padded lesions. A p-value below 0.05 was considered to indicate statistical significance.

1.2.5 K-space Field Map Analysis

For each of the MS patients, a Pearson’s correlation coefficients were calculated between the k-space of the high resolution field map and the k-space of the pre-zero padded field map and the k-space of the high resolution field map and the k-space of the post-zero padded field map. Only the k-space periphery, i.e. the region of k-space that had been zero padded, was included in this analysis. A paired t-test was performed over all MS patients to evaluate whether the high frequency k-space of the pre-zero padded field map was more correlated with the high frequency k-space of the high resolution field map as compared to the high frequency k-space of the post-zero padded field map.

1.3 RESULTS

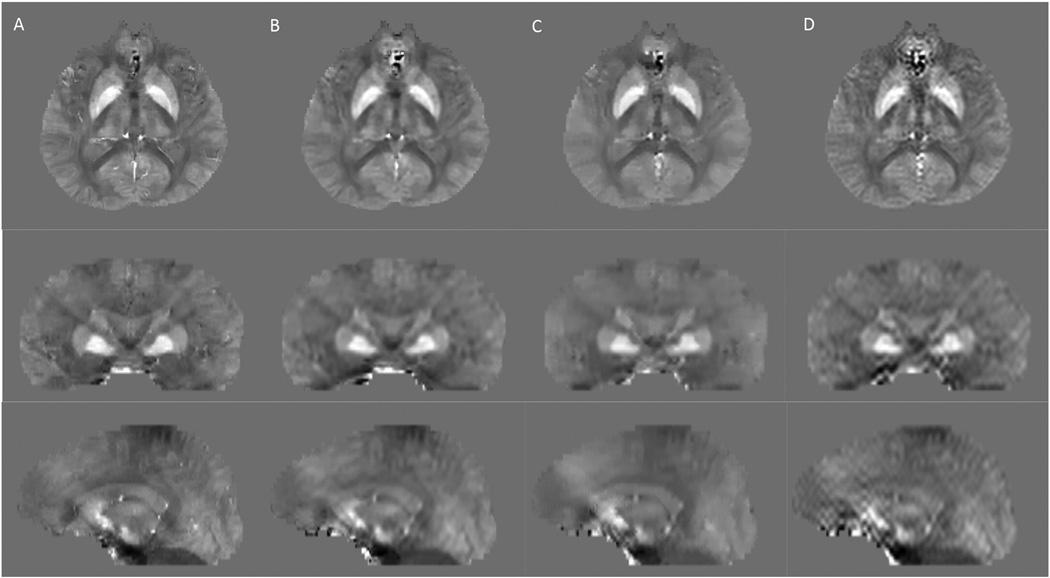
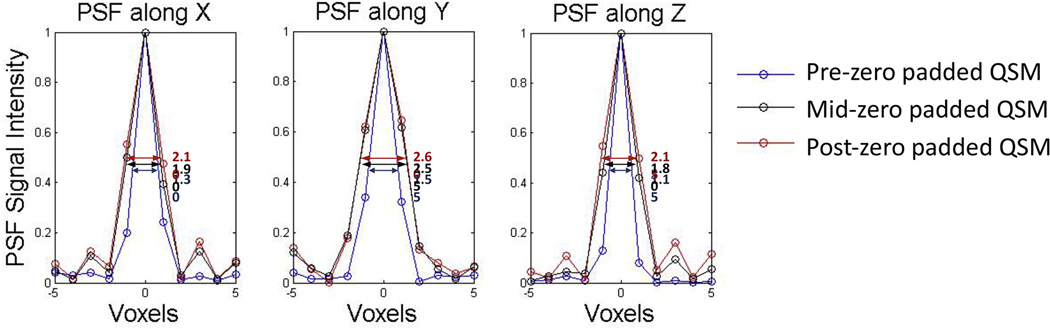
For the healthy subject scan, high resolution QSM, pre-zero-padded QSM, mid-zero padded, and post-zero padded QSM results are displayed in Figure 1. The relative errors over the whole image of the pre-, mid-, and post-zero padded methods as compared to the high resolution QSM were 0.39, 0.47 and 0.51 respectively. The PSFs for each method as compared to the high resolution QSM are displayed in Figure 2. The apparent resolution for the pre-zero padded, mid-zero padded, and post-zero padded methods, as measured by the FWHM of the PSFs, were 1.30, 1.90 and 2.10 voxels along x, 1.55, 2.55 and 2.60 voxels along y, and 1.15, 1.80, and 2.15 voxels along z respectively.

Figure 1.

Figure 1

Open in a new tab

Healthy subject QSM. A) High resolution reconstruction: axial (top row), coronal (middle row) and sagittal (bottom row) sections; (B) Pre-zero-padded low resolution reconstruction; (C) Mid-zero-padded low resolution reconstruction; (D) Post-zero-padded low resolution reconstruction, which has markedly increased streaking artifacts that appears as ringing in axial view and streaking in coronal and sagittal views.

Figure 2.

Figure 2

Open in a new tab

Apparent spatial resolution of pre-, mid- and post-zero padded QSM in a healthy subject. 1D cross sections of the 3D point spread function (PSF) along x, y, and z demonstrate that the pre-zero padded QSM reconstruction (blue) has a higher apparent resolution than the mid-zero padded reconstruction (black), which has a higher apparent resolution than the post-zero padded reconstruction (red). Arrows denote the full-width half-maximums (in units of voxels).

For the MS patient whole brain data, the relative error over the whole image of the pre-zero padded QSM was less than that of the mid-zero padded QSM (pre-zero error: 0.57±0.07; mid-zero error: 0.76±0.09; p= 6e-17), which was less than that of post-zero padded QSM (post-zero error: 0.79±0.09; p=2e-4). The apparent spatial resolution of the pre-zero padded reconstructions, as measured by the FWHM of the PSF for the whole image, was higher than that of the mid-zero padded reconstructions (pre-zero FWHM: 1.27±0.18; mid-zero FWHM: 1.72±0.22; p=5e-19), which was higher than that of the post-zero padded reconstructions (post-zero FWHM: 1.84±0.20; p=3e-7).

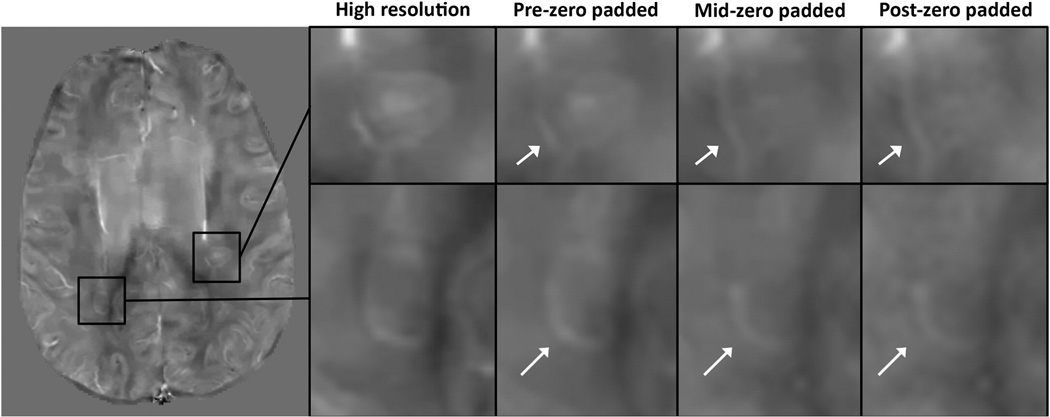
For the MS lesions, pre-zero padded QSM image quality scores (2.56±0.63) were higher than both the mid-zero padded scores (mid-zero scores: 2.02±0.83; p=4e-3), and the post-zero padded scores (post-zero scores: 1.77±0.92, p=9.7e-5). The average mid-zero score was higher than the average post-zero padded score, although this difference was not statistically significant (p=0.57). Two MS lesions magnified in Figure 3 illustrate how pre-zero padded reconstructions more accurately depict lesion geometry than mid- and post-zero padded reconstructions. Furthermore, the relative errors of pre-zero padded lesion ROIs were lower than those of the mid-zero padded lesions (pre-zero error: 0.44±0.24, mid-zero error: 0.58±0.32; p=9e-4), which were lower than those of the post-zero padded (post-zero error: 0.65±0.40; p=4e-6).

Figure 3.

Figure 3

Open in a new tab

MS patient data. High resolution QSM reconstruction displayed on left. On the right, magnified MS lesions reconstructed using the high resolution data, pre-, mid- and post-zero padded QSM methods illustrate that lesion geometry may be better depicted in the pre-zero padded QSM reconstructions than in the mid- and post-zero padded ones.

For the MS patient k-space field map analysis, the correlation coefficients between the high frequency k-space of the high resolution field map and the high frequency k-space of the pre-zero padded field map was higher than the correlation coefficient between the high frequency k-space of the high resolution field map and the high frequency k-space of the post-zero padded field map (p=5e-7).

1.4 DISCUSSION

Our results indicate that QSM image quality, apparent resolution, and accuracy (as measured by decreases in relative error) all increase when zero padding is performed on the complex GRE data before field mapping and QSM reconstruction – pre-zero padding – as compared to when zero padding is performed after field mapping but before QSM reconstruction (mid-zero padding) or after QSM reconstruction (post-zero padding). We demonstrated this effect in a healthy subject, and in a group of MS patients, where pre-zero padded QSM reconstruction resulted in more accurate delineation of MS lesion geometry as compared to post-zero padded QSM. These results suggest that pre-zero padding, rather than post-zero padding, may be an effective way to improve lesion visualization in QSM.

Recent pathological studies have demonstrated that different subclasses of MS lesions may contain different iron distribution patterns (19, 20). Therefore, improving the visualization of lesion geometry on QSM can potentially be used both to distinguish different pathological stages of lesion genesis and to monitor MS disease activity.

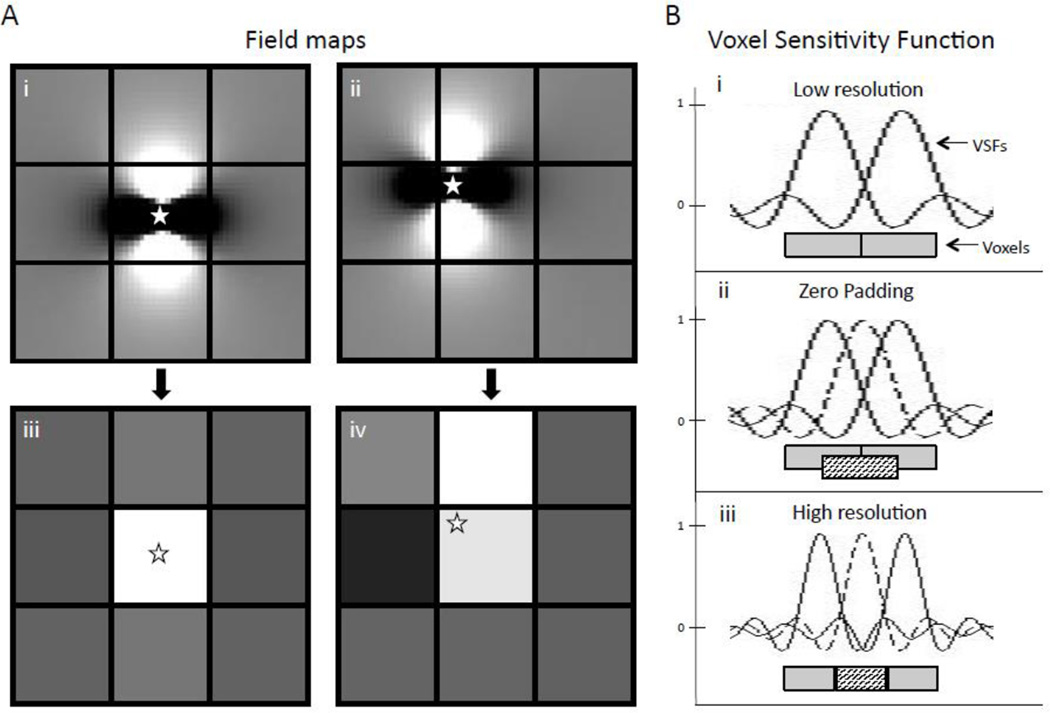
Zero padding is a well-known interpolation technique whereby zeros are added to the periphery of k-space (6, 7), which is equivalent to inserting sinc-interpolated voxels for a smooth display of the wave-like k-space data in image space. Zero padding improves overall image visualization and may enable visualization of small structures at the corner of the voxel, but does not change spatial resolution (6–12). The results in this paper suggest that zero padding of the complex GRE data interacts with several of the nonlinear steps used to obtain a susceptibility map, resulting in improved visualization compared to performing the zero-padding at the end. The QSM algorithm used here includes several nonlinear steps such as field map estimation, phase unwrapping and L1 regularized dipole deconvolution. When these non-linear operations are performed on zero padded data, non-zero high frequency k-space information is introduced into formerly zero padded regions, as is demonstrated in Figure 4. For instance, zero padding prior to phase unwrapping and field map estimation results in an estimated field map with non-zero high frequency k-space data that is a closer approximation of “true” high frequency k-space than are zeroes alone. This may be explained by thinking about these nonlinear steps as introducing prior information, e.g. field map estimation imposes a linear phase over time in each voxel.

Figure 4.

Figure 4

Open in a new tab

Field map estimation, a non-linear transformation, adds non-zero values to the high frequency k-space. A) K-space of the 1st echo of high resolution complex MRI data; B) K-space of the 1st echo of pre-zero-padded complex MRI data. Low frequency k-space is identical to A, but high frequency k-space is set to zero. C) and D) display the k-space of the field maps estimated using A) and B) respectively. Note that D), unlike B), exhibits non-zero high frequency k-space information.

Another way to understand these results is that zero padding followed by nonlinear operations permits deconvolution with a higher resolution dipole kernel, thereby solving the field-to-source inverse problem on a finer grid than that of the acquired data. This enables one to increase the apparent spatial resolution of the final QSM image, since sub-voxel distributions of magnetic susceptibility may result in different field measurements on the original voxel grid (see Figure 5A).

Figure 5.

Figure 5

Open in a new tab

A) Subvoxel shifts in susceptibility affect the field measured in adjacent voxels. i) and ii) show the high resolution field map generated by a single susceptibility source (white star). iii) and iv) show the field measured on the voxel grid, which was derived from summing over the subvoxel fields of i) and ii). B) Zero padding versus increased k-space sampling. i) Voxel sensitivity functions (VSFs) for two adjacent low resolution voxels are shown. ii) Zero padding produces the interpolated black voxel thereby giving higher weighting to small structures at the corner of the low resolution voxel, but the FWHM of the VSF has not changed. iii) Increased k-space sampling decreases the FWHM of the VSF, resulting in a higher resolution image.

As a result, pre-zero padded QSM is closer to high resolution QSM than is mid- or post-zero padded QSM, as measured by apparent spatial resolution, relative error and qualitative image score.

In this study, pre-zero padding was found to provide a more accurate QSM image with higher apparent image resolution without an increase in scan time as compared to post-zero padding. Conversely, this post-processing technique can be used to shorten scan time with a decrease in apparent image resolution that is smaller than would be expected based on the acquired matrix size. We demonstrate a decrease in scan time in the absence of compressed sensing, projection onto convex sets (POCS), etc, but we expect the early zero padding step to act as a plus factor in shortening scan time when these other fast scanning methods are employed.

In conclusion, zero padding of the complex GRE data prior to the nonlinear steps of QSM improves image accuracy and increases apparent image resolution. It also provides better delineation of MS lesion geometry, which may improve lesion subclassification and disease monitoring in MS patients.

Acknowledgments

This research was supported in part by the National Institutes of Health [grant numbers R01EB013443 and R01NS072370].

Abbreviations

QSM

Quantitative susceptibility mapping

GRE

gradient echo

PDF

Projection onto Dipole Fields

MEDI

morphology enabled dipole inversion

ROI

region of interest

PSF

point spread function

FWHM

full-width-half-maximum

PCOS

projection onto convex sets

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

REFERENCES

  • 1.Liu T, Liu J, de Rochefort L, Spincemaille P, Khalidov I, Ledoux JR, et al. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: comparison with COSMOS in human brain imaging. Magn. Reson. Med. 2011;66(3):777–783. doi: 10.1002/mrm.22816. [DOI] [PubMed] [Google Scholar]
  • 2.Langkammer C, Liu T, Khalil M, Enzinger C, Jehna M, Fuchs S, et al. Quantitative susceptibility mapping in multiple sclerosis. Radiology. 2013;267(2):551–559. doi: 10.1148/radiol.12120707. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Khalil M, Teunissen C, Langkammer C. Iron and neurodegeneration in multiple sclerosis. Multiple sclerosis international. 2011;2011:606807. doi: 10.1155/2011/606807. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Langkammer C, Schweser F, Krebs N, Deistung A, Goessler W, Scheurer E, et al. Quantitative susceptibility mapping (QSM) as a means to measure brain iron? A post mortem validation study. NeuroImage. 2012;62(3):1593–1599. doi: 10.1016/j.neuroimage.2012.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Argyridis I, Li W, Johnson GA, Liu C. Quantitative magnetic susceptibility of the developing mouse brain reveals microstructural changes in the white matter. NeuroImage. 2013;88C:134–142. doi: 10.1016/j.neuroimage.2013.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Du YP, Parker DL, Davis WL, Cao G. Reduction of partial-volume artifacts with zero-filled interpolation in three-dimensional MR angiography. Journal of magnetic resonance imaging : JMRI. 1994;4(5):733–741. doi: 10.1002/jmri.1880040517. [DOI] [PubMed] [Google Scholar]
  • 7.Parker DL, Du YP, Davis WL. The voxel sensitivity function in Fourier transform imaging: applications to magnetic resonance angiography. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 1995;33(2):156–162. doi: 10.1002/mrm.1910330203. [DOI] [PubMed] [Google Scholar]
  • 8.Bernstein MA, Fain SB, Riederer SJ. Effect of windowing and zero-filled reconstruction of MRI data on spatial resolution and acquisition strategy. Journal of Magnetic Resonance Imaging. 2001;14(3):270–280. doi: 10.1002/jmri.1183. [DOI] [PubMed] [Google Scholar]
  • 9.Elgavish RA, Twieg DB. Improved depiction of small anatomic structures in MR images using Gaussian-weighted spirals and zero-filled interpolation. Magn Reson Imaging. 2003;21(2):103–112. doi: 10.1016/s0730-725x(02)00642-2. [DOI] [PubMed] [Google Scholar]
  • 10.Forbes KP, Pipe JG, Karis JP, Heiserman JE. Effects of zero-filled interpolation on cervical magnetic resonance angiographic measurement. AJNR American journal of neuroradiology. 2003;24(3):319–322. [PMC free article] [PubMed] [Google Scholar]
  • 11.Lin R, Wu R, Xiao Z, Liu G, Kong K, Lang Z. Zero-filling interpolation processing technique can efficiently suppress segmental stenosis artifact on small arteries of anatomical phantoms. Riv Neuroradiol. 2005;18(2):169–174. [Google Scholar]
  • 12.Zhu XL, Tomanek B, Sharp J. A pixel is an artifact: On the necessity of zero-filling in fourier imaging. Concept Magn Reson A. 2013;42(2):32–44. [Google Scholar]
  • 13.Liu T, Wisnieff C, Lou M, Chen W, Spincemaille P, Wang Y. Nonlinear formulation of the magnetic field to source relationship for robust quantitative susceptibility mapping. Magn. Reson. Medic. 2013;69(2):467–476. doi: 10.1002/mrm.24272. [DOI] [PubMed] [Google Scholar]
  • 14.Liu T, Khalidov I, de Rochefort L, Spincemaille P, Liu J, Tsiouris AJ, et al. A novel background field removal method for MRI using projection onto dipole fields (PDF) NMR in biomedicine. 2011;24(9):1129–1136. doi: 10.1002/nbm.1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Smith SM. Fast robust automated brain extraction. Human brain mapping. 2002;17(3):143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Kressler B, de Rochefort L, Liu T, Spincemaille P, Jiang Q, Wang Y. Nonlinear regularization for per voxel estimation of magnetic susceptibility distributions from MRI field maps. IEEE transactions on medical imaging. 2010;29(2):273–281. doi: 10.1109/TMI.2009.2023787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, et al. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 2010;63(1):194–206. doi: 10.1002/mrm.22187. [DOI] [PubMed] [Google Scholar]
  • 18.Liu J, Liu T, de Rochefort L, Ledoux J, Khalidov I, Chen W, et al. Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map. NeuroImage. 2012;59(3):2560–2568. doi: 10.1016/j.neuroimage.2011.08.082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Mehta V, Pei W, Yang G, Li S, Swamy E, Boster A, et al. Iron is a sensitive biomarker for inflammation in multiple sclerosis lesions. PloS one. 2013;8(3):e57573. doi: 10.1371/journal.pone.0057573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Hametner S, Wimmer I, Haider L, Pfeifenbring S, Bruck W, Lassmann H. Iron and neurodegeneration in the multiple sclerosis brain. Annals of neurology. 2013;74(6):848–861. doi: 10.1002/ana.23974. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES