Explosive genetic evidence for explosive human population growth

Abstract

The advent of next-generation sequencing technology has allowed the collection of vast amounts of genetic variation data. A recurring discovery from studying larger and larger samples of individuals had been the extreme, previously unexpected, excess of very rare genetic variants, which has been shown to be mostly due to the recent explosive growth of human populations. Here, we review recent literature that inferred recent changes in population size in different human populations and with different methodologies, with many pointing to recent explosive growth, especially in European populations for which more data has been available. We also review the state-of-the-art methods and software for the inference of historical population size changes that lead to these discoveries. Finally, we discuss the implications of recent population growth on personalized genomics, on purifying selection in the non-equilibrium state it entails and, as a consequence, on the genetic architecture underlying complex disease and the performance of mapping methods in discovering rare variants that contribute to complex disease risk.

Introduction

Inferring effective population size¹ throughout the history of human populations has been an active research area for decades. Earlier studies based on single nucleotide polymorphisms (SNPs) and microsatellites were able to infer clear historical changes in the size of populations (e.g. [1–7]). However, due to the small sample size (less than 100 individuals) and small number of variants (up to tens of thousands), these pioneering studies had limited power to infer a detailed picture of historical changes in population size.

The improvements in sequencing technologies, especially the advent of “next-generation sequencing” technologies, have made it possible to sequence very large numbers of individuals. Specifically, over 100,000 human whole genomes and over a million human whole-exomes have been sequenced to date. Hence, recent studies of population size changes were based on up to many thousands of sequenced individuals [8–12]. A common thread coming out of the analyses of different large-scale genetic datasets has been the observation of an extreme excess of rare SNPs (commonly defined as those where the minor, less common allele appears in <1% or even <0.1% of the sample) compared with both previous observations and predictions from earlier models of population history [8–14]. Specifically, by analyzing the sequences of 200 genes in over 14,000 individuals, mostly from different European populations, Nelson et al. (2012) [9] reported that over 70% have the minor allele presented in only one or two individuals. Similarly, after whole-genome sequencing of >4,000 individuals from a certain European population, more than 12,000 novel variants are expected with the sequencing of the next individual, which constitutes 0.5% of all heterozygous sites in the newly sequenced individual [14]. The elevated proportion of rare variants has provided a window into very recent history of populations because, as population genetic theory suggests, rare variants are generally younger—due to more recent mutations—than more common variants [13,15,16].

Theoretical development of methods to infer historical population sizes did not lag behind the rapid technological advancement, where numerous methods have emerged over the last decade. The BOX summarizes the different types of approaches focusing as well on specific methods and corresponding software implementations where available. Briefly, the most widely used summary of genetic data for historical population size inference, especially since the sequencing of entire regions became possible, has been the distribution of frequencies of genetic variants, also known as the site frequency spectrum (SFS)². Inference methods that employ the SFS of one or more populations are mostly based on coalescent theory (e.g., [17–22]), though methods based on diffusion approximations (e.g., [23,24]) have also been very successful. The main limitation of SFS-based methods is that they do not use important information from linkage disequilibrium (LD). However, there is no shortage of complementary methods that are based on LD and haplotype information. Many of these methods were built on coalescent and hidden Markov models [25–29] and others incorporate inference of identity-by-descent (IBD) and identity-by-state (IBS) [30–33] (BOX).

BOX. Methods and software for inference of population size changes, including of recent growth.

This box summarizes many of the key methods and software for the inference of population size history. Due to space constraint, this is by no means a comprehensive summary (for a more detailed recent review of methods see for example [70]). In particular, it focuses on methods that are designed to perform inference of population size changes of a population, often with a focus on human populations, and excludes those that target inter-species inferences, as well as present only recent methods and software that are often built on earlier versions that are not discussed.

The methods of interest can be broadly divided into two groups. The first group of inference methods makes use of genetic summary statistics that can be obtained by independently considering each site, mostly the site frequency spectrum (SFS) and mostly by carrying out inference based on setting a parameterized model of history and searching for parameter values that maximize the likelihood (or an equivalent approach) of observing the values of the SFS. Evaluation of the likelihood for each set of parameter values is performed either via simulations or analytical derivation. These methods can be further divided according to whether coalescent theory or diffusion theory is at the basis of this evaluation. These set of methods do not capitalize on the interaction (linkage disequilibrium) between nearby sites, and as such do not require phasing.

Excoffier et al. (2013) [17] extended on previous similar methods in implementing an SFS-based inference approach using coalescent simulations in the software fastsimcoal2. This software supports the simultaneous inference of arbitrary numbers of populations. However, the inference can be computational intractable as the number of populations and/or the number of parameters for inference become large and the desired accuracy increases, which is a general disadvantage of simulation-based methods. Bhaskar et al. (2015) [18] developed a very efficient method and software (fastNeutrino) for inferring population size changes for a single population. The efficiency of stems from analytical computation of the SFS for a set of parameter values of a pre-defined model of population size changes, together with a fast optimization technique. More recently, Kamm et al. (2016) [21] extended this method to multi-populations, maintaining analytical calculation of the SFS is implemented in the software momi (which currently does not support inference, but momi2 will support inference as well; personal communication). Instead of using the SFS, Chen et al. (2015) [19] proposed a method based on the total number of segregating sites in a single population as a function of sample size. Liu and Fu (2015) [20] also infer population size changes of a single population based on the SFS (implemented in stairway plot). However, instead of making assumptions about the number of epochs and shape of each epoch in the history, such as exponential growth as the pre-defined model underlying other inference methods, it approximates historical population size via a non-parametric approach that fits many epochs, each of constant population size, while adding population size changing points (new epoch) until a good fit is obtained. Most recently, similar to fastNeutrino [18], we (2016) [22] developed a method (implemented in EGGS, without inference) that allows an analytical and efficient computation of the SFS for a set of parameters from more generalized models than previously possible, including population growth that is sub- or super-exponential.

Methods based on diffusion approximations rather than coalescent theory include the widely used ∂a∂i software by Gutenkunst et al. [23], which supports the simultaneous inference of population size changes, split times and migration among up to three populations. It uses a finite difference method for estimating the SFS for a set of parameters. Lukic and Hey (2012) [24] introduced a method with the same aim as ∂a∂i (implemented in MultiPop), but that is based on spectral approximation of the SFS by polynomials. Several limitations of diffusion approximations have been shown, such as dramatic increase of inference time as the number of populations increases [21] and the instability of numerically solving the partial differential equations. Methods based on exact diffusion–based calculations that address these limitations will appear in the near future (personal communication with Simon Gravel).

The second group of inference approaches relies on linkage disequilibrium (LD) and haplotype information of genetic sequences, which typically requires the sequences to be phased. Most such methods are based on hidden Markov models.

Li and Durbin (2011) [25] and later Schiffels and Durbin (2014) [28] introduced popular methods (PSMC and MSMC, respectively) for inferring population size changes based on Sequential Markovian Coalescent (SMC) [71,72]. Both methods are non-parametric. PSMC infers the history of a single population using a pair of sequences from the same diploid individual, hence it does not require phasing. It utilizes a hidden Markov model where the observations are the sequences from a diploid genome, the hidden states are times to the most common ancestor (TMRCA) and the transitions represent ancestral recombination events. MSMC (and a newer version MSMC2, personal communication with Richard Durbin and Stephen Schiffels, which, among else, overcomes scaling bias) is an extension of PSMC that can work on the sequences from multiple individuals and also enables the study of the genetic separation between pairs of populations. Coupled with SMC model, Palacios et al. (2015) [73] developed a Gaussian process-based Bayesian non-parametric method to infer population size history from a set of genealogies, which can be estimated by methods that infer the ancestral recombination graphs such as ARGweaver [74]. Sheehan et al. (2013) [26] and then Steinrücken et al. (2015) [29] introduced other methods based on sequentially Markov conditional sampling distribution framework (implemented in diCal and diCal2, respectively). The input to this method is a collection of haplotype sequences. This method optimizes changes in the population size history by iteratively maximizing the conditional probability of observing another unused haplotype in the dataset given the inferred history and the used sequences up to the last round. Two major differences between diCal and diCal2 are: (1) diCal is a non-parametric method, while diCal2 is parametric; (2) diCal can only infer the history of a single population while diCal2 can infer the history of several populations, including splits, mergers and migration.

Another family of methods that rely on LD and haplotype information infer population size history by fitting the distributions of haplotype-based genetic summaries. Palamara et al. (2012) [30] developed a parametric method that fits the distribution of IBD⁶ segment lengths to a population bottleneck followed by recent exponential growth, implemented in the software DoIRS. A more recent study by Browning and Browning (2015) [32] presented a non-parametric method by using inferred long segments of IBD (IBDNe software). Unlike DoIRS, which directly uses the distribution of IBD segment lengths, this method calculates the expected distribution of TMRCAs given an IBD segment length, and uses the total amount of genetic material in IBD segments due to each TMRCA to estimate the effective population size for that TMRCA. This method focuses on the inference of very recent history and can infer the population size at each generation. Harris and Nielsen (2013) [31] developed a parametric inference method by fitting the length distribution of IBS⁷. While very powerful for recent history, a limiting factor for the accuracy of these methods is the quality of IBD or IBS segments, which decreases as they become shorter [75,76]. As shorter segments correspond to less recent events, IBD-based methods are powerful only for the recent past. Additionally, population size estimates beyond the thousands are typically unreliable, as barely any IBD segments descend from periods when the population size is as large [77].

Consensus on ancient changes in size of major human populations

We first provide a brief overview of ancient population size history, since many studies on recent changes in population size make assumptions of ancient events. Several studies have shown that non-African populations have experienced at least two severe population bottlenecks³ in their history, one resulting from the Out-of-Africa event and the other likely around the time of the initial split of European and Asian populations [23,34–36] (Figure 1a). Importantly, different studies reached different estimates for the times and intensities of the population bottlenecks, potentially making the inference of recent history sensitive to the specific values assumed for these ancient events, as discussed in [12,19,22]. Table 1 presents estimates of the more intense, Out-of-Africa bottleneck from three studies that have been later used as the basis for inferring recent changes in population size.

Figure 1. Population growth of major continental human populations.

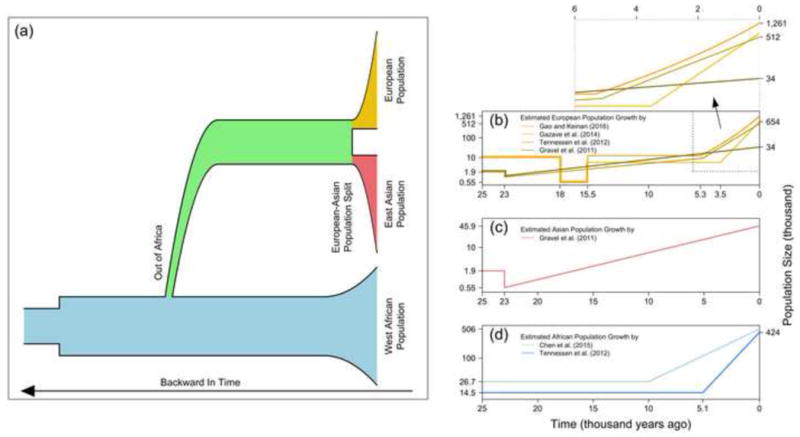
The figure presents the population size of three populations: Europeans, East Asians, and West Africans, over time (with time from right to left, i.e. present at the far right). (a) Schematic illustration of historical population size changes in the three populations. The population size history of the African population is shown in blue. The population history from the Out-of-Africa bottleneck to European-Asian split is shown in green. After the split, the European population is shown in orange and the Asian population in red. Population sizes are broadly represented by the width of the area of each population, but these are merely schematic and do not correspond to any estimated model. For simplicity, we ignored recent evidence of both admixture of human populations [78] and admixture with archaic hominids [79]. (b) Inferred recent population growth in European populations according to the models of Gravel et al. [36], Tennessen et al. [10], Gazave et al. [12], and Gao and Keinan [22]. A further zoom-in of the most recent 6,000 years is presented above this panel and emphasizes the difference between exponential growth (straight lines) and faster-than-exponential growth (concave curve). Due to space limitation, we only selected to plot these four representative models among those discussed in this paper. (c) Inferred recent population growth in an East Asian population by Gravel et al. [36] (to compare with the same model for Europeans in panel b). (d) Recent exponential population growth in a West African population estimated by Tennessen et al. [10] and Chen et al. [19]. Y-axis (on either the left or the right side of the plot) of panels b–d show the estimated population size, on a log scale, with an indication of important values for the included model/s, including assumed values, estimated values, and extant population size. Note the different scale of the y-axis between the three panels. Detailed parameter estimates for these models are presented in Table 2 and described throughout the text. The inferred history plotted in panels b–d focuses on the studies that utilized the SFS to specifically model the recent growth using exponential or generalized models.

Table 1.

Estimates of Out-of-Africa bottleneck from three studies that have been assumed as the basis of studies that inferred recent population growth (see Table 2). For the second, more recent bottleneck we only provide the time it started, to be compared with the Out-of-Africa bottleneck, since studies make different assumptions regarding it and what follows it.

Study	Population Size Prior to Bottleneck	Starting Time of Bottleneck (kya)	Intensity $\left(F=\frac{T}{2N}\right)$a	Time Recent Bottleneck Started (kya)
(1) Schaffner et al. (2005) [34]	24,000	87.5 (fixed in study)	0.085	50 (fixed in study)
(2) Keinan et al. (2007) [35]	10,000	118	0.264	18
(3) Gravel et al. (2011) [36]	14,470	51	0.301	23

^aSee definition in main text.

Rare variants point to recent explosive growth in European populations

European populations have been at the focus for inference of changes in population size due to the availability of large samples of sequencing data. The recently observed excess of rare variants in Europeans has been shown to result from extreme recent growth in population size, as predicted by recent exponential growth [13] and super-exponential growth [15]. An earlier study [8] based on sequencing two genes in 10,000 Europeans assumed the ancient European history of Schaffner et al. (2005) [34], including a recent population size of 7,700, and inferred an exponential growth from that population size starting 1.4 (95% Confidence Interval (CI): 0.9–2.8) thousand years ago (kya)⁴ with a growth rate of 9.4% (4.5%–14.5%) per generation, entailing 1.1 million individuals at present (Table 1). Based on the sequencing of 202 drug target genes in 14,000 individuals from a variety of European populations, Nelson et al. (2012) [9] assumed the same ancient history and estimated exponential growth starting 9.3 kya with a rate of 1.7% (1.2%–2.3%) per generation, entailing 4 (2.5–5) million individuals at present (Table 1). In a parallel study, based on exome sequencing data of 1,351 Europeans, as part of the Exome Sequencing Project (ESP), Tennessen et al. (2012) [10] assumed the ancient history of [36], and estimated two separate recent epochs of exponential growth to accommodate the possibility of accelerated growth, which is supported by the census data [13]. Their estimates point to a mild growth during the first epoch—which is assumed to start at a fixed time of 23 kya, corresponding to a European-Asian split according to [36]—at a rate of 0.307% (0.301%–0.313%)⁵. This mild growth epoch, starting with ~1,000 individuals and ending with ~9,000 individuals, essentially corresponds to the recovery from the second bottleneck in models assumed by other studies, whether that growth is instantaneous or exponential. The second epoch was estimated to exhibit much more extreme growth of rate 1.95% (1.35%–2.55%) starting 5.1 kya, leading to a current population size of about 0.5 million (Figure 1b; Table 2). While all these studies considered the SFS, Chen et al. (2015) [19] considered the total number of segregating sites as a function of sample size (BOX). Based on an updated version of the same ESP dataset with an expanded number of individuals and assuming the timing of ancient events from [12], they estimated one epoch of exponential growth, starting 7.3 (6.95–7.55) kya at a rate of 1.49% (1.11%–1.87%) and leading to a current population size of 1.20 (1.09–1.31) million, only broadly consistent with the second epoch estimated by [10] using the same data (Table 2). While exact parameter estimates are different between the different studies, which is partially due to the assumed model of ancient history [12,19], they all clearly point to explosive growth in European population size that culminates in an extant effective population size on the order of magnitude of a million individuals.

Table 2.

Detailed parameter values for recent population size growth inferred in the studies discussed in this review. The table focuses on parametric inference methods. All these are based on methods that fit a model to the SFS, with the exception of one based on the number of segregating sites (Chen et al. (2015)) and one based on IBD segment distribution (Carmi et al. (2014)) (BOX). The results of additional studies, including based on non-parametric inference, are described in the main text. The numbers in parentheses indicate 95% confidence interval of parameter values if available from that study.

Population	Ancient Model Assumeda	Study	Sample Size	Variants Analyzed	Recent Growth Starting Time (kya)		Growth Rate (%)
European	(1)	Coventry et al. (2010) [8]	10,000	2 Genes	1.4 (0.9, 2.8)		9.4 (4.5, 14.5)
	(1)	Nelson et al. (2012) [9]	14,002	202 Genes	9.3		1.7 (1.2, 2.3)
	(3)	Tennessen et al. (2012) [10]b	1,351	Whole Exome	5.1		1.95 (1.35, 2.55)
	(2)	Gazave et al. (2014) [12]	500	Neutral variants (216 kb)	3.5		3.4
	(2)c	Chen et al. (2015) [19]	4,298	Whole Exome	7.3 (6.95, 7.55)		1.49 (1.11, 1.87)
	(2)	Gao and Keinan (2016) [22]	4,300	Whole Exome	Exponential	4.95 (4.88, 5.05)	2.2 (2.15, 2.26)
					Super-exponential	5.33 (5.15, 5.5)	NAd
Ashkenazi Jewish		Carmi et al. (2014) [45]	128	Whole Genome	0.7 (0.63, 0.8)		30 (16, 53)
African		Tennessen et al. (2012) [10]	1,088	Whole Exome	5.1		1.66 (1.6, 1.72)
		Chen et al. (2015) [19]	2,217	Whole Exome	10 (9.6, 10.4)		0.74 (0.6, 0.88)
Asian		Gravel et al. (2011) [36]	40	Whole Genome	23 (21, 27)		0.48 (0.3, 0.75)

^aFor European Population only, indicates the model of historical changes in population size that is assumed prior to estimating recent growth. The model number corresponds to Table 1, where the ancient model is further described.

^bTennessen et al. (2012) models recent growth in the European population by two epochs, a more ancient mild growth followed by the recent explosive growth. The values here are for the estimated recent explosive growth, with the less recent one corresponding to the recovery from the recent bottleneck in other models, including in the ancient model it is based on.

^cChen et al. (2015) applied an ancestral model that has the same skeleton of (2), but the population size parameters for the bottlenecks and recovery epochs were inferred, while only the times remained fixed on the assumed model.

^dGao and Keinan (2016) inferred recent growth using an exponential model and a generalized model, with the estimates of the latter pointing to faster-than-exponential growth. In that case, the growth rate is not defined, while the growth speed has been estimated to be 12% (7%–15%) faster than the estimated exponential that is reported in the table.

All of the above studies were based on protein-coding genes, in which variants are affected not only by population size history, but also by natural selection. In fact, some of these same studies have also shown that purifying (negative) selection that acts on deleterious alleles can result in an excess of rare variants [9,10], which is similar to the effect of population growth. Hence, most inference studies based on protein-coding genes used only synonymous variants to minimize this confounding effect. However, it has been shown that sysnoymous variants are often not strictly neutral [9–11,38–41]. Furthermore, beyond the direct effect of selection, background selection, i.e. the effect on neutral SNPs due to being linked to sites under selection, can also distort their allele frequencies in a manner similar to exponential growth [42]. To study recent history with minimal confounding by these forces, a recent study [12] generated and made available the Neutral Regions dataset, which consists of 500 individuals of North-Western European ancestry sequenced at regions where variants are putatively neutral [43], spanning a total of 216 kb. These regions are very far from genes and other potentially coding loci, outside segmental duplications, copy number variants and CpG islands, and of low conservation and repetitive element content. Based on these data, they assumed the ancient model of [35] and estimated both a recent epoch of exponential growth and the population size prior to growth, pointing to growth starting 3.5 (2.9–4.1) kya at a rate of 3.4% (2.4%–5.1%) per generation, resulting at 0.65 (0.30–2.87) millions individuals today (Figure 1b; Table 2).

All of the above studies estimated and assumed a single recent epoch of exponential growth, with one study [10] attempting to describe acceleration in the rate of recent growth by modeling two such epochs. Two recent studies considered the theoretical impact of growth that is super-exponential (accelerating) or sub-exponential (decelerating) on the SFS and developed software for simulating genetic sequences under these scenarios, also including the cases of exponential growth, population decline, and constant population size [15,44]. More recently, we presented an analytical solution for the SFS under a framework in which each growth epoch in history—not just the most recent one as in the above—has been generalized allowing for super- and sub-exponential forms as above, but also linear growth and a variety of other scenarios [22]. Hence, the implementation of the framework of [22] (BOX) side steps the need to run simulations and allows for a quick analytical evaluation of the SFS which facilitates inference based on real data. Applied to synonymous variants from the recent version of ESP data [11], and assuming the ancient model of [35], it inferred one epoch of recent growth, with the estimate of growth start time and population size parameters generally consistent with the above studies [22]. However, growth speed was estimated to be 12% (7%–15%) faster than exponential growth, suggesting growth that is accelerating moderately compared to exponential growth [22] (Figure 1b; Table 2).

Recent explosive growth based on other types of inference methods and for additional populations

Using their IBD-based method IBDNe (BOX), Browning and Browning (2015) [32] considered population growth in two European populations, 5,200 individuals from the UK and 5,402 Finnish individuals. While all the above results have been based on sequencing data in order to capture the statistics (mostly the SFS) with little ascertainment bias, IBD-based methods, such as in this study, can be based on genotype data. They estimated population size for each generation during the last 50 generations (~1250 years) and showed that the UK population had grown from ~0.1 million to 27 (21–34) million individuals during this time. Similarly, the Finnish population grew from about 3,000 individuals to 0.38 (0.33–0.46) million, with the growth occurring mostly during the last 15 generations (375 years) [32], consistent with the re-population of Northern Finland about 300–500 years ago. Also based on IBD (BOX), Carmi et al. (2014) [45] used whole-genome sequencing of 128 individuals to estimate the recent bottleneck and population growth of Ashkenazi Jews (Jews from Eastern Europe). They estimated a severe founder event 700 (630–800) years ago, with the population consisting of only 330 (250–420) individuals, followed by exponential growth with an extreme growth rate of 34% (16%–53%) per generation, which results in an extant population of 1.45 million individuals (Table 2).

Evidence of recent exponential growth has been observed in non-European populations as well. Based on exome of 1,088 African Americans and accounting for their recent admixture, Tennessen et al. (2012) [10] showed that their modeled African population experienced exponential growth starting 5.1 kya with a rate of 1.66% (1.6%–1.72%) per generation, concluding with an extant population size of ~0.42 million (Figure 1d; Table 2). With an updated version of the same ESP dataset, which includes a larger sample size, Chen et al. (2015) [19] estimated the onset time of African population growth to be about 10 (9.6–10.4) kya with growth rate of 0.74% (0.60%–0.88%) per generation (Figure 1d; Table 2). Based on whole-genome sequencing of only 40 individuals from the 1000 Genomes pilot data [46], Gravel et al. (2011) demonstrated that East Asian populations (Han Chinese and Japanese combined) experienced a mild growth starting about 23 (21–27) kya with a rate of 0.48% (0.30%–0.75%) per generation, leading to an extant population size of 45,900 (Figure 1c; Table 2). This mild growth mirrors their estimated current European population size of 34,000, where a similar sample size has been used. As shown above, with much larger sample size that allows observing variants of much lower frequency, this model of European history has been expanded to predict more extreme growth and much larger extant population size [10] (Figure 1b; Table 2). It remains to be re-estimated for East Asians with a much larger sample size.

Results of non-parametric methods for estimation of population size changes

Studies that use non-parametric approaches for inference of population size changes can potentially still point to general trends of growth. For example, applying the MSMC method to whole-genome sequences from each of the 9 populations with European, Asian, African and Native American ancestry, for a total of 34 individuals, Schiffels and Durbin (2014) [28] showed population size changes that generally support population growth after the Out-of-Africa event. However, the estimated population size fluctuates greatly in recent history, specifically during the last few thousand years, which is when explosive growth is expected based on both the historical record [12,13] and the results of parametric studies reviewed above. The reason for MSMC’s results being inaccurate during recent time is the availability of few haplotypes at that time, with the point estimate for the extant population size being especially unreliable due to the nature of the methodology (personal communication with Stephan Schiffels and Richard Durbin). Another recent non-parametric method, stairway plot by Liu and Fu (2016) [20] has been tested on the whole-genome sequencing of each of 9 populations from 1000 Genomes Project phase 1 data [47]. A recent trend of growth after the Out-of-Africa is clearly reflected in the results [20]. However, recent explosive growth was not observed since the results during the last 10,000 years are inaccurate, and have actually been excluded from the figures, since (as per personal communication with Xiaoming Liu) the inference power of very recent history is highly influenced by singletons, for which calling is less reliable in the analyzed low-coverage sequencing data.

Discussion

The increasing availability of next-generation sequencing data with large sample sizes has uncovered more rare variants and, hence, allowed the characterization of recent explosive growth. Some statistical methods are limited in making use of such huge amount of data and some assumptions made by current models start to break down. Hence, these types of data have opened avenues for theoretical research and development of new methods. For example, researchers have started to study the effect of multiple-and simultaneous-coalescent events on the SFS—the probability of which increases with increasing sample size—which have been ignored by traditional coalescent-based inference methods [48–50]. Bhaskar et al. (2014) [48] showed that these events have an effect on the SFS, hence it would be important to incorporate more sensitive coalescent-based inference in future study.

The ever-increasing data sizes can also make amenable similar analyses of the X chromosome, despite its size and the relatively small number of variants it carries. This is a promising topic for future research considering that recent years have shown the importance of learning about genetic history also based on the sex chromosomes, and particularly by contrasting results from the autosomes to those based on the sex chromosomes [51–60]. Specifically, several studies showed that the ratio of population size of chromosome X to that of the autosomes is, at times, significantly different from the expected ¾ [51,52,54,56,57,61]. Interestingly, due to the smaller allelic sample size, chromosome X is expected to be affected more by more recent epochs [52,62]. Beyond the X chromosome, a recent study provided likely the most comprehensive view of male history using Y-chromosome sequences [60]. However, all studies described in this review have focused on studying the autosomes alone, and our own attempt to replicate some of these studies for the X chromosome indeed lacked enough statistical power with existing data. Any unexplained differences in population genetics of the autosomes and the sex chromosomes during the recent epoch of explosive growth—which can be revealed with much larger datasets and/or new methods—might point to differences between the roles of males and females in population growth or to effects of natural selection during that epoch.

As in other “big data” fields, with increasing data, machine-learning techniques have gained some traction also in population genetics. For example, deep learning has been utilized recently to jointly infer population size changes and selection in Drosophila [63] and can be similarly applied to data from human populations. Overall, with the combination of emerging novel methods and high-quality large-scale genetic sequencing, we expect a much more refined and accurate picture of population size history to be inferred in the near future for many more populations, and with the ability to focus on more and more recent history and to account for the X chromosome, admixture events, and joint-analysis of many populations. (See Figure 1’s legend for known admixture events that are ignored by the studies reviewed herein.)

Implications

One consequence of recent explosive growth is the extreme excess of very rare variants, including those observed only in a single genome out of a large sample (singletons). In fact, explosive population growth predicts not only more rare variants, e.g. singletons, as the sample size increases, but also a larger proportion of such variants (e.g. [13,14]). A recent study characterized how population growth and purifying selection has shaped the fraction of variants private to an individual, hence the number of new variants that will be discovered with each newly-sequenced individual [14]. Assuming 10,000 genomes from the exact same population have already been perfectly sequenced, with growth of the magnitude estimated for Europeans [12] it predicts > 6,000 novel variants to be discovered as heterozygous in the 10,001^st sequenced genomes, which is 18-times more than that in the absence of growth. This entails that personalized medicine or personalized genomics will have to be much more personal in recently expanded populations than expected in the absence of growth.

Several studies have examined the effect of explosive growth on the impact of purifying selection against deleterious mutations and how the two interact in affecting the genetic architecture of human complex disease and other complex traits [64–67]. Generally, deleterious mutations that are still polymorphic are expected to be of lower frequency if affected by purifying selection. A recent study [64] carried out computer simulations to test how purifying selection operates in the non-equilibrium state of explosive population growth and described the implications it has on the load of deleterious mutations in populations today. It concluded that due to explosive growth, the population as a whole carries orders of magnitude more deleterious rare mutations but that each individual is expected to carry only a slightly larger fraction of deleterious variants than in the absence of growth. It further showed the efficiency of selection that due to the larger population size in reducing the frequency of the very deleterious variants, resulting in each individual carrying variants that are a little less harmful than otherwise expected. A more recent study conducted simulations under different scenarios, including capturing the effect of growth on deleterious mutations in several models [65]. The pertaining results are in line with those described above [64]. One seeming contradiction is that this study reported that following explosive growth each individual carries a smaller number of deleterious mutations overall, which is the case since very weakly deleterious mutations are considered as neutral rather than deleterious [65].

Several studies showed that recent growth can increase the amount of additive genetic variance for a disease or trait accounted for by very rare variants under certain genetic architectures, where variants under purifying selection are implicated in diseases or other traits such that their effect is harmful [13,66–68]. Considering that rare variants arose recently, this implies that the causal variants of such traits more likely to vary between different populations due to population growth. Recent growth may also hamper the ability to map causal variants, with fewer being significant in standard single-variant association testing [13,66]. Hence, sequence-based rare variant association studies (RVAS) combine all variants in a functional unit (e.g. a gene; an exon) or another locus and apply any of a number of tests that consider an association of the variants in aggregate. However, a recent study reported that such tests also suffer from a loss of power under scenarios with recent growth, and that super-exponential growth results in an even greater decrease in power [67]. These findings suggest that accounting for recent population history will be important when considering the power of different types of association studies in different populations and that ever larger samples will be required to map rare variants in populations that have recently expanded.

To close on an optimistic note, while complicating association studies, contributing to a deleterious load in populations, and challenging personalized medicine, the excess rare variants and their population-specificity have a thick silver lining for population geneticists: They facilitate a refined study of different populations and their relationship that is not possible based on more common variants. Specifically, population structure can be inferred on a finer-scale, which is demonstrated both theoretically and by application to 4,298 whole exomes from European Americans (ESP dataset) by O’Connor et al. (2015) [69]. It shows that while each rare variant provides little information for inferring population structure, their large number facilitates more powerful and finer-scale inference, which resulted, for example, in the discovery of a sub-population of Ashkenazi Jews in the ESP dataset [69]. Another example of a silver lining is the improved power for IBD segment detection in the presence of many rare variants since the sharing of a very rare variant provides strong support for IBD [32].