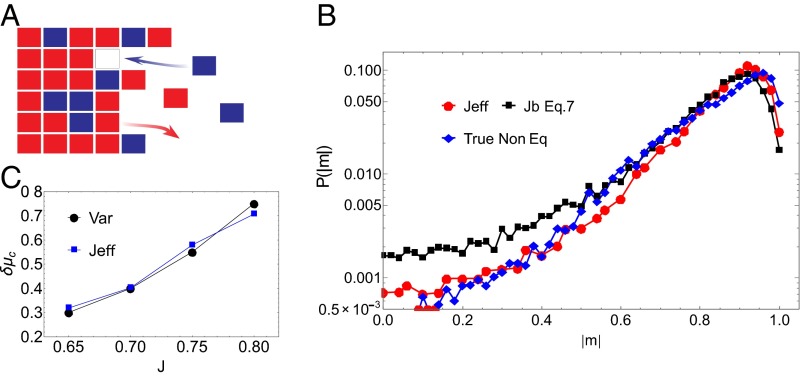
Fig. 2.

Application of the bounds to the nonequilibrium 2D growth process. (A) We assemble a 2D configuration from a monomer bath containing red and blue blocks. The energy of interaction between similar monomers is ${ϵ}_s$, whereas that between dissimilar monomers is ${ϵ}_d$. As discussed in the main text, when the assembly is grown at equilibrium, the statistics of compositional fluctuations in the assembly are equivalent to that of an Ising magnet with coupling constant $J=\frac{{ϵ}_s-{ϵ}_d}{2}$. (B) We compare the value of critical driving force $\delta {\mu }_c$ obtained by computing $J_{eff}$ using the Onsager solution, as described in the main text, with that obtained by computing the variance of magnetization fluctuations as described in ref. 24. The agreement between the two estimates confirms that the system has anomalously large fluctuations at the nonequilibrium critical driving force we identify. (C) We calculate the probability of magnetization from the nonequilibrium simulations and compare it with distribution obtained by sampling an Ising model at $J_{eff}$ and $J_b$ from Eq. 7. These data were obtained for $J=0.65$ and $\delta \mu =0.1$. The system grows rapidly for these parameters as evidenced by the value of $J_{eff}$ computed for these parameters. We expect the system to be far from linear response. The close agreement between the distribution predicted by $J_b$ and the nonequilibrium distribution, even far from the mean, suggest that our theoretical bound indeed accurately captures the fluctuations in this nonequilibrium system.