Structural quality of unrefined models in protein docking

Abstract

Structural characterization of protein-protein interactions is essential for understanding life processes at the molecular level. However, only a fraction of protein interactions have experimentally resolved structures. Thus reliable computational methods for structural modeling of protein interactions (protein docking) are important for generating such structures and understanding the principles of protein recognition. Template-based docking techniques that utilize structural similarity between target protein-protein interaction and co-crystallized protein-protein complexes (templates) are gaining popularity due to generally higher reliability than that of the template-free docking. However, the template-based approach lacks explicit penalties for inter-molecular penetration, as opposed to the typical free docking where such penalty is inherent due to the shape complementarity paradigm. Thus, template-based docking models are commonly assumed to require special treatment to remove large structural penetrations. In this study, we compared clashes in the template-based and free docking of the same proteins, with crystallographically determined and modeled structures. The results show that for the less accurate protein models, free docking produces fewer clashes than the template-based approach. However, contrary to the common expectation, in acceptable and better quality docking models of unbound crystallographically determined proteins, the clashes in the template-based docking are comparable to those in the free docking, due to the overall higher quality of the template-based docking predictions. This suggests that the free docking refinement protocols can in principle be applied to the template-based docking predictions as well.

INTRODUCTION

Structural characterization of protein-protein interactions is essential for our ability to understand and manipulate biomolecular processes. Structures of protein-protein complexes are more difficult to determine experimentally than structures of the individual proteins. Moreover, proteins potentially participate in multiple protein-protein interactions, making the number of protein-protein prediction targets much larger than that of the individual proteins. Thus, only a fraction of known protein-protein interactions has experimentally resolved structures.¹ Modeling is essential for generating such structures, as well as for learning the principles of molecular recognition and structure/function relationships.

Prediction of protein-protein structures (protein docking) aims at determining the spatial arrangement of the target proteins within the complex, given the structure (experimentally determined or modeled) of the individual proteins, in the general case, without any other a priori information on the docking mode. The docking protocols usually consist of the global scan (global search for an approximate structure of the complex) with a coarse-grained, computationally inexpensive objective function, followed by scoring/refinement of the putative matches, using more accurate functions and structural adjustment.^2,3 For computational efficiency, the scan is often rigid-body, whereas the refinement may involve conformational sampling of the internal degrees of freedom. In terms of the intermolecular energy, the scan typically means the global, landscape-wide search for the intermolecular energy funnel, and the refinement is the local minimization within that funnel.^4,5

In free docking, the scan is performed by sampling of the protein relative positions across the intermolecular landscape, either explicitly (e.g., Monte Carlo moves⁶), or implicitly (e.g., correlation by Fast Fourier Transform - FFT⁷). In the template-based (comparative) docking, the scan is sequence or structure alignment of the target proteins to the pool of templates - co-crystallized protein-protein complexes (template detection). The free docking, typically, is explicitly based on the surface complementarity paradigm, which searches for the maximal surface match, and penalizes structural penetrations. Thus, the structural penetrations of the putative matches are relatively small, and amenable to structural refinement protocols based on energy minimization. To remove the clashes, rigid-body moves with the side-chains repacking may be sufficient for proteins with moderate conformational changes upon binding.^6,8,9 For difficult targets, backbone flexibility can be accounted for by low-frequency normal mode analysis,^10–13 backbone perturbations using the fold-tree-based method,¹⁴ and semi flexible refinement of interface residues in torsion angle space followed by Cartesian dynamics refinement in explicit solvent.¹⁵

As opposed to the free docking, the template-based docking is based on a different premise - the one of similarity of the protein folds, and does not include penalty for structural penetration. Thus the scan output of the template-based docking may contain severe structural penetrations (clashes), e.g. in the case of variable loop conformations in otherwise similar proteins. With such structural overlaps, typical refinement protocols, which effectively amount to energy minimization, would be ineffective, having to deal with infinite energies in very large areas of the search space.

Despite increasing popularity of the template-based docking, a systematic analysis of the clashes, which can be used in development of procedures for their removal, is lacking. In this paper, we compare and analyze the extent of clashes in unrefined template-based and free docking of crystallographically determined unbound proteins and protein models. The results show that for the less accurate protein models, free docking produces fewer clashes than the template-based approach. However, contrary to the common expectation, in acceptable and better quality docking models of unbound crystallographically determined proteins, the clashes in the template-based docking are comparable to those in the free docking, due to the overall higher quality of the template-based docking predictions. This suggests that the free docking refinement protocols can in principle be applied to the template-based docking predictions.

METHODS

The free docking was performed by the rigid-body FFT protocol as implemented in GRAMM.^7,16 Top 100,000 matches from the scan stage with 3.5 Å spatial grid step, and 10° angular step were scored by Miyazawa-Jernigan (MJ3h) statistical potential,¹⁷ and 1,000 matches with the lowest MJ3h energy were retained for further analysis.

The template-based docking protocol, developed previously in our lab¹⁸ utilizes experimentally determined structures of protein-protein complexes (templates) for full structure alignment to the target proteins by TM-align.¹⁹ The algorithm performs a systematic search for best templates in the template library²⁰ composed of 4,950 co-crystallized binary complexes from DOCKGROUND.²¹ Models with any of the two TM-scores < 0.4 and the fraction of contacts shared by the target and the template < 0.05 were previously shown to be unreliable,^1,22 and thus were removed from the final pool of predictions.

The free and the template-based docking was performed on the unbound set 3²³ and model set 2²⁴ from DOCKGROUND. The unbound set consists of 102 protein-protein complexes and the unbound structures of each protein. The set of protein models is composed of 165 binary protein-protein complexes with each monomer represented by six models with increasing levels of inaccuracy (model-to-native C^α RMSD 1 ± 0.2 Å, 2 ± 0.2 Å,…, 6 ± 0.2 Å), and the co-crystallized bound structure of each complex as reference.

RESULTS AND DISCUSSION

The purpose of the global scan in docking is detection of the protein-protein matches that can be further refined by local minimization. This means that such matches have to be inside the intermolecular energy funnel (see Introduction). Thus the size of the funnel limits the accuracy of the scan output (distance from the native structure at the bottom of the funnel) amenable for local minimization.⁵ Methods of measuring the size of the funnel^5,25 are consistent in their estimates for its upper bound of ~10 Å ligand RMSD (L-RMSD). This is also consistent with the range of the electrostatic and desolvation energies in protein-protein complexes.²⁵ Thus, in this study, we deal with the docking predictions within such limit, focusing on the community accepted Critical Assessment of Predicted Interactions (CAPRI) quality criteria for docking predictions.²⁶

To quantify the amount of clashes in the docking models, an intersection of van der Waals volumes, ΔV_vdw, of the two interacting proteins was calculated for their projection onto a cubic grid with 1.0 Å step (the van der Waals radii according to Ref ²⁷). To obtain a quantity that is independent of the interface size, we normalized ΔV_vdw by the average solvent-accessible surface area buried upon the complex formation (this quantity hereafter referred to as average penetration, d_av).

$$d_{\text{av}}=\frac{\mathrm{\Delta }{V}_{\text{vdw}}}{(\mathrm{\Delta }{\text{SASA}}_{AB}+\mathrm{\Delta }{\text{SASA}}_{BA})/2},$$ (1)

where ΔSASA_ij is solvent-accessible surface area of protein i screened from the solvent by protein j. The severity of clashes in docking models was calculated as the maximal penetration, defined as follows. For every point x⃗ on ΔSASA_AB, the closest point y⃗ on ΔSASA_BA is determined, and the maximum of these distances represents the maximal penetration of the two proteins

$$d_{max}=\underset{\overrightarrow{x}\in {\text{SASA}}_{AB}}{max}\left(\underset{\overrightarrow{y}\in {\text{SASA}}_{BA}}{min}\Vert \overrightarrow{x}-\overrightarrow{y}\Vert \right)-2.8Å$$ (2)

Since the solvent-accessible surface can be considered as the molecular surface “inflated” by the radius of a water molecule (1.4 Å), a correction of 2 × 1.4 Å is introduced in Eq. (2) to eliminate the effect of mutual penetrations of the water shells. Rapid calculation of solvent-accessible surfaces was achieved by Le Grand and Merz algorithm²⁸ and the use of k-d trees²⁹ for quick retrieval of spatially adjacent atom pairs.

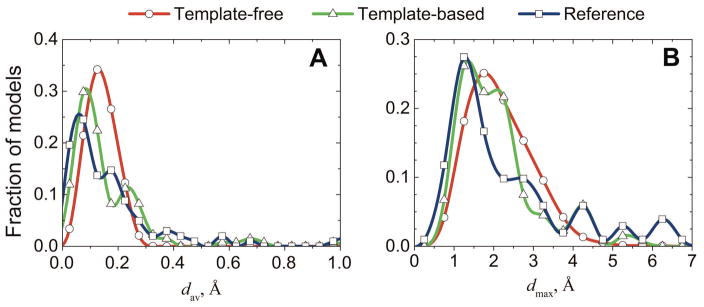
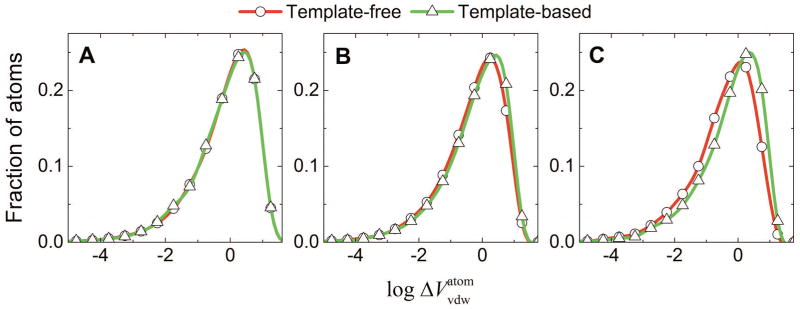
The unbound structures of 102 protein-protein complexes from the DOCKGROUND benchmark set were docked by the free and template-based docking protocols (see Methods). Models of acceptable and higher quality (according to CAPRI criteria²⁶) were retained in both protocols, resulting in the pools of 2,513 and 134 models for the free and the template-based predictions, correspondingly. The template-based docking yielded on average 3, and maximum 65 near-native matches per target. The corresponding numbers for the free docking were 39 and 227. At least one near-native match was produced for 40 and 65 targets by the template-based and the free docking, respectively. Despite different paradigms of the two methodologies (shape complementarity in free docking and fold similarity in template-based docking), most models had clashes with comparable average and maximal penetrations, with only a minor increase of clashes in the template-based predictions (Fig 1). The composition of the clashes (side-chains vs. backbones) was also similar (Fig 2).

Figure 1. Clashes in docking of unbound proteins.

For 102 complexes in DOCKGROUND Benchmark 3, 2513 free docking and 134 template-based docking predictions of acceptable and higher quality were assessed by average (A) and maximum (B) penetrations, calculated from Eqs 1 and 2, respectively. Reference is the distribution of clashes in the 102 reference complexes obtained by superimposition of the two unbound protein structures onto corresponding proteins in the co-crystallized complex.

Figure 2. Side chain and backbone clashes in docking of unbound proteins.

Volumes of intersections $\mathrm{\Delta }{V}_{\text{vdw}}^{\text{atom}}({Å}^3)$ were calculated for each pair of overlapping atoms, based on their radii and the interatomic distance. The distributions were obtained for 201,422 and 12,827 pairs of side-chain atoms (A), 191,700 and 14,937 pairs of backbone and side-chain atoms (B), and 28,982 and 4,466 pairs of backbone atoms (C) in free and template-based docking, respectively.

The average penetration d_av introduced in this study, is strongly correlated with the number of clashing atom pairs (atom pairs with overlapping van der Waals spheres), normalized by the buried SASA of the interface (Pearson’s correlation coefficient 0.99 for the template-based, and 0.94 for the free docking). This equals to 15 – 20 clashing atom pairs per 100 Ų of ΔSASA in the unrefined docking predictions of acceptable or better quality.

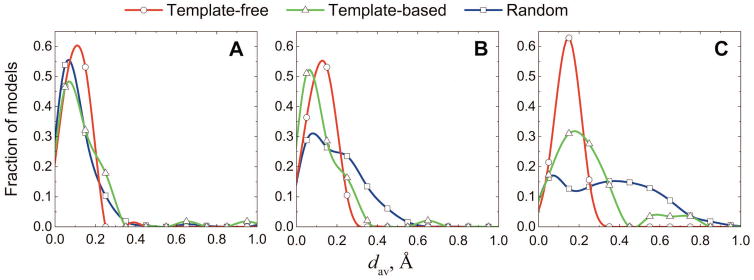
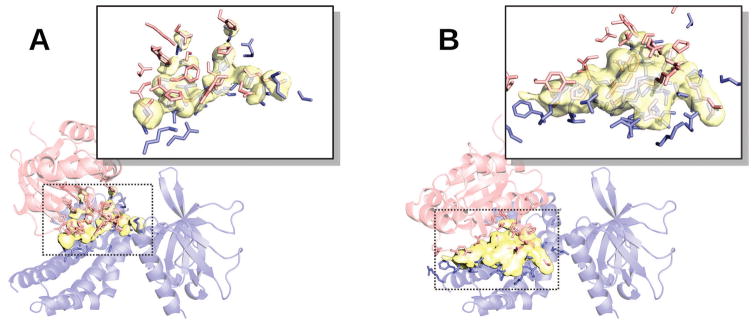
Most free docking predictions are of acceptable quality (1,967 out of 2,513), whereas most template-based predictions are of high and medium quality (56 and 49 out of 134, correspondingly). For the free docking predictions the amount of clashes is almost independent of the docking quality, whereas less accurate docking predictions by template-based docking have more clashes than the more accurate ones (Fig 3). The largest discrepancies in the amounts of clashes between free and template-based docking are observed for predictions of acceptable quality (Fig 3C, and an example in Fig 4).

Figure 3. Clashes in docking of different quality.

Distributions of average penetrations (Eq. 1) are shown separately for high (A), medium (B), and acceptable (C) quality models (according to CAPRI criteria). Plots are obtained for 32, 514, 1967 free and 56, 48, 29 template-based high, medium, and acceptable quality predictions, respectively. The reference distributions were obtained from the analysis of clashes in random models. For each target with at least one free or template-based prediction within a certain quality category, ten random models (one for targets with acceptable free models) of the same quality were generated (see text and Figure 5).

Figure 4. Example of clashes in acceptable quality docking predictions.

Docking was performed by free (A) and template-based (B) protocols. Unbound structures corresponding to 2nz8, chains A and B, from DOCKGROUND Benchmark 3 were used. The unbound structure 1mh1, chain A, is in blue, and the unbound structure 1nty, chain A is in red. Overlapping van der Waals volumes are in yellow. The interface side-chains selected at 3 Å cut-off are in sticks. Average, d_av, and maximum, d_max, penetrations are 0.15 Å and 1.62 Å for the free and 0.58 Å and 3.80 Å for the template-based predictions, respectively.

To understand whether the observed differences are significant, one needs a baseline that shows how many clashes are generally expected in a prediction of a given quality, regardless of the docking method used to produce it. To acquire such baseline, we generated docking matches of pre-defined quality by randomly translating (t⃗) and rotating (U) the ligand multiple times until the match was in the desired CAPRI category (Fig 5). For each quality category, the distribution of clashes in these matches yields characteristic distributions of d_av, which are not biased towards any specific docking method. We generated ten random models of a protein-protein complex for each complex yielding acceptable or higher quality docking predictions (Fig 5). The amount of clashes in the random models decreases with the increase of the docking quality (thin lines in Fig 3). The random docking models have a larger amount of clashes than both free and template-based predictions. In all quality categories, the clashes in the template-based predictions are closer to the clashes in the random docking models than to the clashes in the free docking, which inherently include the penalty for the clashes (Fig 3).

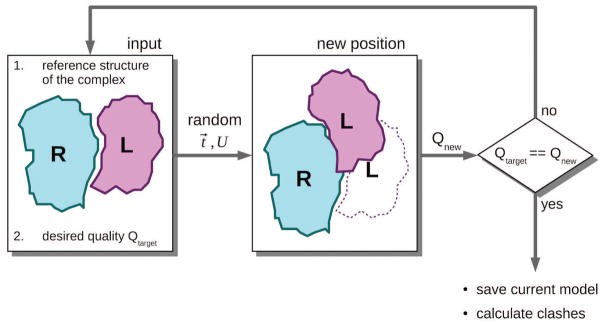
Figure 5. Flowchart of random model generation.

Given two proteins in their reference positions (overlapped with the co-crystallized monomers), and the intended quality Q_target (high, medium, or acceptable), the procedure repeatedly generates a model by randomly translating (translation vector t⃗) and rotating (rotation matrix U) the ligand L with respect to the receptor R. At each trial, the quality Q_new of the complex RL’ is calculated. The procedure is repeated until the model with the intended quality is obtained.

Conditions that define each CAPRI quality category restrict the receptor-ligand configuration space to an area around the native state of the complex, resulting in the upper limit for the clashes (d_av and d_max ≤ 1.2 Å and 7.0 Å, respectively, in any of the docking predictions analyzed). Thus, clashes in a near-native prediction produced by any rigid-body docking method are inherently restricted to this limit. Therefore, a minimization procedure capable of removing clashes in this area from the random models should be sufficient for the predictions of free or template-based docking.

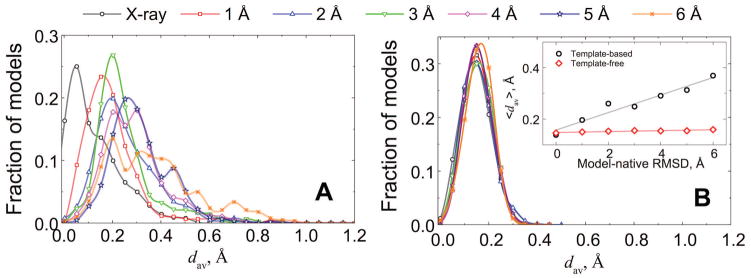
In the structural reconstruction of protein-protein interaction networks, most docked complexes would consist of individual protein models.³⁰ Deviations of such models from the native structures could significantly exceed the structural variations observed in the proteins upon binding (e.g., the average interface C^α RMSD between bound and unbound conformations.³¹) Thus, we also analyzed clashes in the docking predictions generated from our benchmark set of protein models²⁴ (Fig 6). The decrease in protein structural accuracy yields increasing amounts of clashes in the template-based docking. Although the template-based docking success rates are weakly dependent on the proteins accuracy, the docking predictions of highly distorted protein models are mainly in the acceptable quality category,²² with such predictions characterized by a larger amounts of clashes (Fig 3). Due to the free docking paradigm that penalizes clashes, it yields docking predictions, on average, with a constant amount of clashes, regardless of the monomer’s accuracy (inset in Fig 6).

Figure 6. Clashes in docking of modeled proteins.

Protein models are from 165 complexes in the DOCKGROUND model set 2. Distributions of average penetrations, d_av (Eq. 1), in the template-based (A) and free (B) docking predictions of acceptable and higher quality are shown separately for each accuracy level of protein models (1 to 6 Å RMSD from the corresponding native structures). For reference, the plot shows d_av distribution of docking predictions from the co-crystallized bound proteins. The inset shows the mean values of the main panel distributions along with corresponding mean values of d_av distributions in free docking of the same set of modeled proteins.

CONCLUSIONS AND FUTURE DIRECTIONS

Without explicit constraints on structural penetration, the template-based docking predictions are more likely to have clashes than the free docking predictions. Indeed, for the less accurate models of the individual proteins, the free docking produces fewer clashes than the template-based approach. However, because of the generally higher quality of the template-based predictions, the clashes in the free and the template-based docking of the crystallographically determined unbound proteins are overall similar. Thus approaches to structural refinement of the docking predictions developed for the free docking, should in principle be applicable to the template-based docking. In our future studies we plan a systematic comparative evaluation of the refinement protocols for the free and template-based docking output.