Absolute cross-sections for DNA strand breaks and crosslinks induced by low energy electrons

Abstract

Absolute cross sections (CSs) for the interaction of low energy electrons with condensed macromolecules are essential parameters to accurately model ionizing radiation induced reactions. To determine CSs for various conformational DNA damage induced by 2–20 eV electrons, we investigated the influence of the attenuation length (AL) and penetration factor (f) using a mathematical model. Solid films of super-coiled plasmid DNA with thicknesses of 10, 15 and 20 nm were irradiated with 4.6, 5.6, 9.6 and 14.6 eV electrons. DNA conformational changes were quantified by gel electrophoresis, and the respective yields were extrapolated from exposure–response curves. The absolute CS, AL and f values were generated by applying the model developed by Rezaee et al. The values of AL were found to lie between 11 and 16 nm with the maximum at 14.6 eV. The absolute CSs for the loss of the supercoiled (LS) configuration and production of crosslinks (CL), single strand breaks (SSB) and double strand breaks (DSB) induced by 4.6, 5.6, 9.6 and 14.6 eV electrons are obtained. The CSs for SSB are smaller, but similar to those for LS, indicating that SSB are the main conformational damage. The CSs for DSB and CL are about one order of magnitude smaller than those of LS and SSB. The value of f is found to be independent of electron energy, which allows extending the absolute CSs for these types of damage within the range 2–20 eV, from previous measurements of effective CSs. When comparison is possible, the absolute CSs are found to be in good agreement with those obtained from previous similar studies with double-stranded DNA. The high values of the absolute CSs of 4.6 and 9.6 eV provide quantitative evidence for the high efficiency of low energy electrons to induce DNA damage via the formation of transient anions.

I. Introduction

In radiotherapy, the energy imparted per unit mass (i.e., the radiation dose) to different tissues and organs by the energetic primary photons or fast charged particles must be known to maximize destruction of cancer cells, while minimizing side effects.¹ The primary particles initiate the production of secondary species, including a large number of secondary electrons² as well as ions, radicals and excited states of the irradiated molecules.³ Monte Carlo (MC) methods are usually preferred to simulate the production of these initial reactive species and the subsequent reactions engendered in biological materials.³ Liquid water has received considerable attention and has been modelled quite successfully.^4,5

In the case of complex targets, such as DNA, the molecule can be superimposed over the liquid water track structure of the MC calculation to obtain the yields of various types of damage arising from the species produced in the liquid solution.⁶ Such a simulation provides data on the indirect effects of radiation, but the damage produced directly by the radiation-induced reactive species from molecules other than water are not included. A priori, to simulate the direct effect of radiation on a biomolecule, the absolute cross-sections (CSs) for all scattering events of the high-energy particles, and secondary electrons, with the target biomolecule embedded in a water medium, are required, particularly those leading to biologically significant lesions.^3–5 These CSs could then be fed into the MC code as input parameters and so provide absolute yields of temporal and spatial evolution of reactions and the species produced by the direct effect of radiation along the tracks.

Electrons with less than 30 eV represent the vast majority of secondary electrons created along high-energy particle tracks.² Thus, CSs for such low energy electrons (LEEs) are needed to estimate the chemical and biological consequences of the direct effects of radiation in cells and radiotherapy. They are essential to provide a quantitative description of the energy deposited by any type of high-energy particle at the nanoscopic level. These CSs are of particular importance in targeted radio-nuclide therapy (TRT). Usually in TRT, radioisotopes emitting Auger electrons are administered to patients via pharmaceutical carriers aimed at the cancer cells.^7–9 When bound to or incorporated into the DNA of cells, these radiopharmaceutical agents are highly radiotoxic, since the emitted Auger electrons produce biological effects comparable to those induced by alpha particles, which have a high linear energy transfer (LET).^10,11 In this type of radiotherapy, optimal treatment requires the knowledge of the energy deposited by such agents at the single-cell level, with emphasis on sub-cellular critical structures. In patient treatments with targeted Auger emitters of high atomic number, the radionuclide decays by electron capture or internal conversion processes, both of which create a cascade ejection of many Auger electrons (e.g., 5 and 25 electrons are released on average per decay of ⁶⁷Ga and ¹²⁵I, respectively).^12,13 Most of these electrons have energies less than few hundreds of eV and ranges on the order of 10 nm in biological media.¹⁴ Those with energies above the ionization potential of water, and those of biomolecules in the cells, generate another distribution of LEEs, which necessarily have high density considering the nanoscale dimensions of the reaction volume. The local density of LEEs becomes even larger if the targeted radionuclides are combined with gold nanoparticles¹⁵ or embedded in gold nanocages.¹⁶ In this case, most of the radiation energy is transformed into kinetic energy of LEEs.¹⁷ High local densities of LEEs are also produced in positron emission tomography (PET); since in this case, the emitted positron must be short range in order to provide high spatial resolution. Hence, CSs for LEE-induced damage may also be of considerable value to calculate the local absorbed doses in PET and help better understand the biological consequences of radiation-based imaging.

For relatively simple targets, one may introduce in the code calculations of electron–molecule scattering, but these are usually free from multiple scattering effects present in the condensed phase.^18,19 At the experimental level, techniques have been developed to measure product yields and effective CSs for LEE interactions within condensed matter.²⁰ In these techniques, the molecules are deposited on a metal substrate by vapour condensation, sublimation, molecular self-assembly and freeze drying (lyophilisation). A flux of LEEs, provided by an external electron source under ultrahigh vacuum conditions, is incident on the molecular solid film.²¹ Depending on the apparatus, the measured signal includes scattered electrons,²² trapped anions²⁰ or the yields of products remaining in the film.^21,23,24 The latter can be measured by liquid chromatography,²³ mass spectrometry²⁴ and gel electrophoresis.²¹ The CS in the condensed phase necessarily depends on the environment, including the band structure and molecular ordering.²¹

In the past decade, most LEE-induced damage yields on complex biomolecules in films were measured with the DNA molecule.^25,26 While these measurements provided valuable information on LEE–DNA interactions, most measured CSs were effective in the sense that they depended on film thickness.^27–29 Considering that the thermalization distance or attenuation length (AL) of a LEE lies within the 10 nm range,¹⁴ only a few monolayers of DNA with a double helix diameter of about 2–3 nm in a film are needed to absorb the energy of the incident particle. Thus, because of electron energy losses along the path of the LEE in the film, the CS for DNA damage depends on the film thickness. Secondly, some LEEs can terminate their path in intermolecular traps, stabilize on a molecule, or via dissociative electron attachment (DEA) stabilize as atomic or radical anions. These phenomena usually cause film charging,^30–32 which depends on the film thickness. So far, such effective CSs for condensed films of supercoiled plasmid DNA have been directly obtained from quantifying the configurational changes in the plasmid as a function of irradiation time t (i.e., exposure–response curve).^27,29

Recently, Rezaee et al. developed a molecular survival model, which can extract from LEE impact experiments on thin films the total damage CS independent of film thickness and charging.³³ As an example, these authors derived the “absolute” CS for DNA strand breaks induced by 10 and 100 eV electrons within lyophilised plasmid DNA films. The ALs needed for the calculations were obtained from exposure–response curves recorded as a function of the film thickness. From these ALs and film thicknesses, the critical parameter of the model (i.e., the penetration factor ( f )), which depends on the film thickness, density, uniformity and morphology could be derived and applied to convert an effective CS measured at a given energy to an absolute CS. In its present form, the model of Rezaee et al.³³ is useful to derive absolute CSs for the sum of all types of conformational damage (i.e., the loss of the initial supercoiled (LS) configuration of plasmid DNA).

In the present study, we show that the mathematical formulation of Rezaee et al. can easily be adapted to generate absolute CSs for specific DNA damage induced by LEEs. In addition to the absolute CSs for LS, we generate absolute CSs for the formation of single strand breaks (SSB), crosslinks (CL) and double strand breaks (DSB) induced by electrons of energies 4.6, 5.6, 9.6 and 14.6 eV, typical for the low-energy range. The electrons are incident on lyophilized plasmid DNA films with thicknesses varying between 10 to 20 nm. The effective CS and AL are shown to depend strongly on the film thickness. The f factor, which can be used to transform an effective CS into an absolute one, also depends on the film thickness, but is found to be independent of electron energy in the investigated range. We show that from this behavior of f, it is possible to transform previously measured effective CSs, in the range of 2–20 eV, into absolute ones. When comparison is possible, the latter are found to be in good agreement with previous measurements.

II. Experimental method

The experimental details of sample preparation, irradiation, and post-irradiation analysis techniques employed in the present studies have been reported in detail elsewhere.^21,34,35 Here, we provide a brief description of the most pertinent elements.

Plasmid DNA [pGEM-3Zf(—), 3197 base pairs, ca. 1 968 966 amu per plasmid] was extracted from Escherichia coli JM109 and purified with a HiSpeed plasmid Maxi kit (QIAGEN). The purified plasmid consisted of 96% supercoiled, 1% concatemeric, 1% nicked circular and 2% crosslink forms. The concentration of DNA relative to the quantity of proteins in the plasmid solution was calculated by measuring the absorption ratio of 260 nm and 280 nm light with a spectrophotometer (BioTek, Epoch). The ratio was 1.92, which corresponds to a purity greater than 90%.³⁶ The TE buffer (Tris–EDTA: 10 mM/1 mM) was separated from DNA by gel filtration with a Sephadex G-50 medium. The final solution consisted of DNA with about 10% proteins and ddH₂O after the filtration.

The DNA solution was separated into three parts and each of them was further diluted in ddH₂O to obtain concentrations of 30, 45, and 60 ng μl⁻¹ DNA. To make 10, 15 and 20 nm thick films of the plasmid, 7 μl of these solutions were deposited onto clean tantalum (Ta) substrates (7 × 20 mm). The latter consisted of a thin layer (450 × 50 nm) of Ta sublimated onto either a 0.4 mm thick silicon wafer or clean borosilicate glass. The deposited samples were placed on a liquid-nitrogen cooled surface and frozen at ~−70 °C for 10 minutes in a glove box held under dry nitrogen. Afterwards, they were dried under a pressure of 5–7 mTorr with a hydrocarbon-free pump for 2 hours to form solid films. The films were circular in shape with 4 ± 2 mm average diameter. Using the known density of 1.7 g cm⁻³ for plasmids extracted from E. coli, their average thicknesses were estimated to be 10, 15 and 20 nm.

The present method does not allow measuring the orientation of the DNA in the film. Such measurements can be made by atomic force microscopy, when the plasmids are ordered by self-assembly.³⁷ In this case, they lie parallel to the surface. As shown by electron stimulated desorption of anions from self-assembled monolayers of DNA,³⁸ orientation could influence LEE-induced damage near the film surface, since the initial electron capture probability is expected to depend on the orientation of the electron beam with respect to that of the basic units within DNA.³⁹ We also note that electrons of 4.6 and 9.6 eV produce no or very few secondary electrons when hitting the Ta surface.

The samples were inserted into holders on a rotary platform inside an UHV chamber equipped with an electron irradiator. The chamber was also filled with dry nitrogen to avoid any contamination by hydrocarbons and water from the atmosphere. The samples were inserted into holders on a rotatory platform inside an UHV chamber equipped with an electron irradiator. Afterwards, the chamber was evacuated for 24 hours, with a hydrocarbon-free turbomolecular pump, to a pressure of 5 × 10⁻⁹ Torr at room temperature. By changing the potential between the sample target (ground) and the center of the filament of the LEE gun, the electron energy could be varied from 2 to 20 eV. The films were bombarded at 5, 6, 10 and 15 eV, with an electron current of 6 nA hitting a surface area on the substrate larger than the DNA sample. The current density of the beam was 3 × 10¹¹ electron s⁻¹ cm⁻² and exposure times varied from 5 to 60 s. Four control samples were placed into the irradiator chamber and left un-irradiated, to serve as the data point at zero fluence in exposure–response curves. The energy scale was calibrated within −0.5 eV by taking, as the zero electron energy reference, the onset of electron transmission through the uncharged film. At this onset, the potential measured between the point of emission of the filament and the substrate was +0.4 V, due to differences in work function between the connections in our apparatus and the DNA–vacuum interface. By subtracting 0.4 V from the voltages (5, 6, 10 and 15 V) initially measured between the filament and the metal substrate one obtains the absolute energies of 4.6, 5.6, 9.6 and 14.6 eV for the impinging electrons.

After irradiation, the samples were removed from the chamber and immediately dissolved in 10 μl of ddH₂O. A comparison of the amount of recovered DNA with the original solution showed that nearly 98% of the deposited DNA was recovered from the substrate. The different structural forms of DNA (i.e., supercoiled, nicked circular and linear forms corresponding to non-deformed DNA, SSB and DSB) and CL in the samples were separated by agarose gel electrophoresis. The DNA samples and the agarose gels were stained with SYBR Green I in the concentration of 100× and 10 000×, respectively. The samples were passed on 1% agarose gel in 1× TAE buffer at 100 volts for 7 minutes followed by 75 volts for 90 minutes (5 V cm⁻¹). The gels were then scanned with a STORM 860 scanner (Molecular Dynamics) adjusted for the blue fluorescence mode at an excitation wavelength of 450 nm and a PMT voltage of 800 in the normal sensitivity mode. The amount of each structural form of the DNA was analyzed using ImageQuant (Molecular Dynamics) software. The binding efficiencies of SYBR Green I for the same amount (75 ng) of supercoiled and linear DNA were measured to establish a correction factor for the weaker binding of SYBR Green I to supercoiled DNA. A multiplication factor of 1.2 was applied to the quantification of supercoiled DNA.

III. Calculation of cross-sections for DNA strand breaks

In the present study, absolute CSs for LEE-induced LS, SSB, DSB and CL to plasmid DNA are derived from the survival model developed by Rezaee et al.³³ For a monoenergetic incident electron beam with a uniform surface current density J₀ impinging on a molecular film, the current density J(x) at a depth x inside the film, after bombardment for time t, is given by:

$$J(x,t)=J_0{\mathrm{e}}^{-\frac{x}{\lambda }}{\mathrm{e}}^{-\frac{t}{\tau }}$$ (1)

where λ is the AL, which depends on the incident electron energy and τ a film charging time constant.^40,41 The total percentage of intact molecules in a film of thickness h after bombardment for time t is obtained from

$$P(t)=P_0\frac{1}{h}{\int }_0^h{\mathrm{e}}^{-\sigma J_0\tau \left(1-{\mathrm{e}}^{-\frac{t}{\tau }}\right){\mathrm{e}}^{-\frac{x}{\lambda }}}\mathrm{d}x$$ (2)

where P₀ is the percentage of intact molecules in the film before irradiation and σ is the CS to change the supercoiled configuration (i.e., LS).³³ Simulations of P(t) vs. time with different values of the parameters indicate that the slopes of the exposure–response curves for different τ at t = 0 are the same;³³ i.e., the initial (t = 0) rate of decrease of the concentration of the target molecules is independent of film charging. Therefore, for sufficiently short irradiation times, the charging should have a minimal effect on the slope of an exposure–response curve. Under this condition, the initial slope P′(0) is given by

$$P^{\prime }(0)=-P_0\sigma J_0\left(\frac{\lambda }{h}\right)\left(1-{\mathrm{e}}^{-\frac{h}{\lambda }}\right).$$ (3)

At a specific electron energy, the AL (i.e., λ) can be determined from the ratio R_1,2 of the initial slope of exposure–response curves (P₁′(0), P₂′(0)) between two different thicknesses h₁ and h₂:

$$\begin{array}{l}{R}_{1,2}(\lambda )=\frac{{P_1}^{\prime }(0)}{{P_2}^{\prime }(0)}=\frac{-P_{01}\sigma J_0\left(\frac{\lambda }{h_1}\right)\left(1-{\mathrm{e}}^{-\frac{h_1}{\lambda }}\right)}{-P_{02}\sigma J_0\left(\frac{\lambda }{h_2}\right)\left(1-{\mathrm{e}}^{\frac{-h_2}{\lambda }}\right)}\\ =\frac{-P_{01}{h}_2\left(1-{\mathrm{e}}^{\frac{-h_1}{\lambda }}\right)}{-P_{02}{h}_1\left(1-{\mathrm{e}}^{\frac{-h_2}{\lambda }}\right)}.\end{array}$$ (4)

Since P and h are known experimental parameters, it is possible to obtain a statistical average value for λ by repeating the analysis for all possible pairs (i.e., from three thicknesses in our experiment). From the average value of λ, the penetration factor f is derived as³³

$$f=\frac{\lambda }{h}\left(1-{\mathrm{e}}^{-\frac{h}{\lambda }}\right).$$ (5)

The penetration factor corresponds to the last two terms of eqn (3) so that:

$$P^{\prime }(0)=-P_0\sigma J_{0}f.$$ (6)

The total conformational damage to DNA (LS) consists of SSB, CL, DSB and any other damage not detected by electrophoresis that changed the supercoiled configuration. The initial slope of these types of damage is denoted as P′(0)_SSB, P′(0)_CL and P′(0)_DSB, respectively, and because of the linearity of eqn (6), the various absolute CSs for DNA strand breaks σ_SSB, σ_CL and σ_DSB are readily obtained from:

$$\begin{array}{l}{\sigma }_{\text{LS}}={\sigma }_{\text{SSB}}+{\sigma }_{\text{CL}}+{\sigma }_{\text{DSB}}+{\sigma }_{\text{other}}=-\frac{P^{\prime }{(0)}_{\text{LS}}}{P_0{J}_{0}f}\\ =\frac{P^{\prime }{(0)}_{\text{SSB}}+P^{\prime }{(0)}_{\text{CL}}+P^{\prime }{(0)}_{\text{DSB}}+P^{\prime }{(0)}_{\text{other}}}{P_0{J}_{0}f}=\frac{{\sigma }_{\text{eff}(\text{LS})}}{f}.\end{array}$$ (7)

Each term in eqn (7) can be assigned to the corresponding σ_SSB, σ_CL, and σ_DSB. Similarly, the effective CS (σ_eff) for each type of conformational damage can be correlated to the corresponding initial slope via ${\sigma }_{\text{eff}}=-\frac{P^{\prime }(0)}{P_0{J}_0}$. In other words, any effective CS measurement of a given conformational damage can be converted to an absolute CS via the factor f, if the film thickness and electron energy are well characterized. If within a given energy range f does not vary, then it becomes possible to determine absolute CSs from effective CSs recorded at different energies, as long as the absolute CS and f are known for a single energy within this range.

IV. Results and discussion

A. Yields and ALs for LEE-induced DNA damage

According to previous measurements of yield functions between 2 and 20 eV, strong resonances appear at 4.6 and 9.6 eV in the effective CS for SSB formation and at 5.6 eV and 9.6 eV for the induction of DSB.³⁴ The existence of core-excited transient anions in the DNA and its subunits at these energies dictated our choice of electron impact energies. A higher value of 14.6 eV was also chosen to represent a region devoid of resonances.³⁴

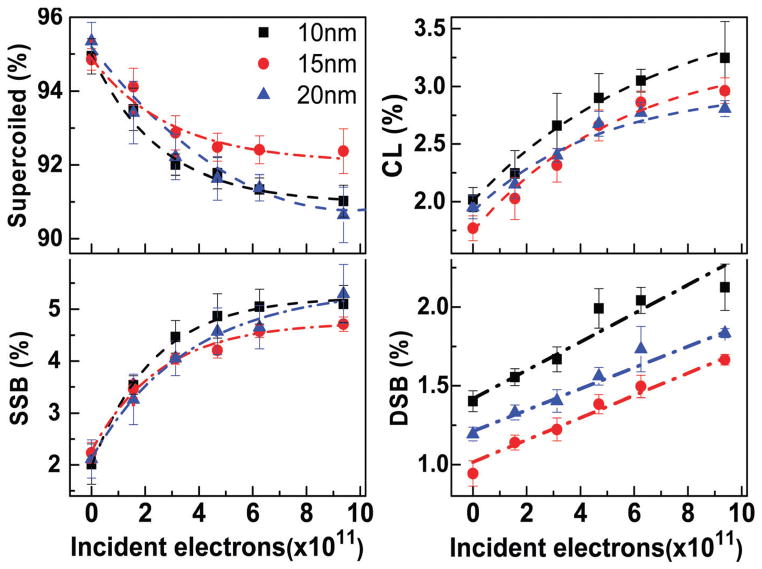
An example from 9.6 eV electron bombardment of the measured exposure–response curves is presented in Fig. 1. It shows the percentage of LS, SSB, DSB and CL as a function of the total number of incident electrons impinging on 10, 15 and 20 nm-thick films of lyophilized plasmid DNA. The percentage of supercoiled DNA decreases (i.e. LS) with electron bombardment, as the molecules are primarily transformed into the nicked circular configuration via SSB. At short exposures, the curves for LS, SSB and CL exhibit a near-linear behaviour. The slopes of these curves become less steep and tend toward a saturating value with increasing fluence, due to film charging. The yields of DSB display a linear function, since the number of initial targets leading to DSB does not change appreciably within the irradiation exposure range (i.e., both supercoiled and circular DNA can lead to DSB). Probably due to the detection limit, no change in the number of DSB could be seen at energies of 4.6 and 14.6 eV. The result is consistent with previous studies, where a resonance in the DSB yield function at 5.6 eV increases the damage, but yields cut off below 5 eV and they are weak between 11 and 15 eV.³⁴

Fig. 1.

Exposure–response curves for lyophilized plasmid DNA films of 10 (■), 15 (●) and 20 (▲) nm average thickness, irradiated with 9.6 eV electrons. The measurements are expressed in percentage of supercoiled, SSB, CL and DSB configurations. The dash-point lines are guides for the eye. Each data point corresponds to the mean value of six electrophoresis results from six different samples with the corresponding standard deviation.

Table 1 presents the ratios of initial slopes of exposure–response curves for LS as defined by eqn (4). The ratios are given for thicknesses of 10, 15 and 20 nm and 4.6, 5.6, 9.6, and 14.6 eV electrons. The values of λ deduced from eqn (4) for each ratio are also provided in Table 1 with the average. The ratios yield progressively smaller λ values as the film thickness increases at all energies. The AL depends on the film uniformity, density, morphology and the targeted biomolecule. The latter three factors are not expected to change much with different amounts of DNA in the lyophilisation process. It has been shown, however, that the uniformity of lyophilized films varies considerably.⁴² As the thickness increases, the percentage of variation in h with respect to the total thickness decreases and we expect the lack of film uniformity to have less influence on the value of AL. Thus, the variation of AL with thickness probably arises principally from the local variations in film thickness.

Table 1.

Attenuation lengths (λ) for 4.6, 5.6, 9.6 and 14.6 eV electron impact on plasmid DNA films

Energy (eV)	Ratioa			λ (nm)
	R10,15	R10,20	R15,20	λ1	λ2	λ3	Average ± SD
4.6	1.12 ± 0.2	1.33 ± 0.24	1.19 ± 0.23	17.98	13.14	9.32	13.5 ± 4.3
5.6	1.32 ± 0.54	1.66 ± 0.70	1.25 ± 0.42	15.14	10.34	6.60	10.7 ± 4.3
9.6	1.12 ± 0.11	1.31 ± 0.2	1.17 ± 0.19	16.51	14.01	11.71	14.1 ± 2.4
14.6	1.11 ± 0.28	1.28 ± 0.41	1.15 ± 0.35	19.45	16.24	13.50	16.4 ± 3.0

^aSubscripts denote the thickness of the DNA films.

SD = standard deviation.

All average values of λ can be considered similar within standard deviations. Nevertheless, we expect the longer AL to be found at 14.6 eV, as seen in Table 1, due to the absence of transient negative ions (TNI) at this energy.³⁴ TNI increase the electron–molecule interactions leading to higher total energy-loss CS, which shorten the AL. The AL value for 9.6 eV electrons can be compared to those previously reported by Rezaee et al.³³ and Boulanouar et al.³⁷ (i.e., 10.4 ± 5.4 nm and 14.1 ± 5.4, respectively). It is particularly encouraging to find that the present AL of 14.1 ± 2.4 nm is in excellent agreement with that of 14.1 ± 5.4 nm obtained from diaminopropane (Dap)-DNA films,³⁷ whose thickness was verified to be highly uniform by AFM.

B. Penetration factor (f) and absolute CS

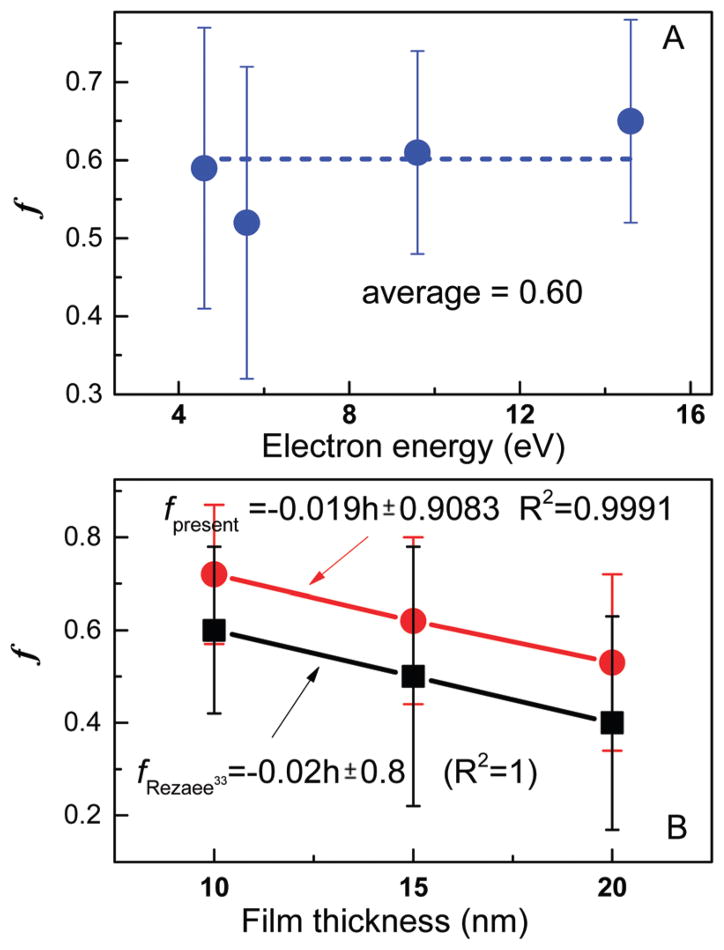
As shown from the model of Rezaee et al., for h/λ ≤ 2, which corresponds to our film thicknesses, the effective CS can be corrected by a factor f to remove the effect of film thickness. Based on eqn (7), the absolute CSs of DNA damage can be calculated from the initial slope of the exposure–response curves, when λ and f are known. As seen from the values in Table 2, the calculated absolute CSs for a given energy are, as expected, similar for three different film thicknesses and ALs. Table 2 presents absolute CSs for LS, SSB, DSB and CL calculated from the results obtained with DNA films of different thicknesses irradiated with 4.6, 5.6, 9.6 and 14.6 eV electrons. All types of damage have maximum values at 9.6 eV. The σ_DSB and σ_CL are about one order of magnitude smaller than those of LS and SSB, indicating that a majority of supercoiled DNA transforms into SSB. The σ of 9.6 and 4.6 eV are larger than those of 5.6 and 14.6 eV. The results are consistent with previous studies³³ suggesting that the first two energies correlate with the formation of TNI in DNA that decay preferentially into inelastic channels leading to the formation of SSB. The average f values for various LEE energies and thicknesses are plotted in Fig. 2.

Table 2.

Absolute CSs for the loss of the supercoiled configuration and the formation of SSB, DSB and CL by 4.6, 5.6, 9.6, 14.6 eV electrons. SD denotes the standard deviation of the CS at each thickness

Electron energy (eV)	Film thickness (nm)	σLS (×10−14 cm2)	σSSB (×10−14 cm2)	σDSB (×10−15 cm2)	σCL (×10−15 cm2)
4.6	10	4.31	3.84	n.d.	4.6
	15	4.46	3.62	n.d.	4.8
	20	4.27	3.73	n.d.	4.7
	Average + SD	4.34 ± 0.10	3.73 ± 0.11	—	4.7 ± 0.1
5.6	10	2.98	2.36	4.1	5.6
	15	2.65	1.92	3.4	6.0
	20	2.51	1.88	3.1	5.5
	Average + SD	2.71 ± 0.24	2.05 ± 0.27	3.5 ± 0.5	5.7 ± 0.3
9.6	10	5.06	4.76	4.5	8.0
	15	5.14	4.57	4.1	7.4
	20	5.04	4.39	4.4	7.2
	Average + SD	5.08 ± 0.05	4.57 ± 0.18	4.3 ± 0.2	7.5 ± 0.4
14.6	10	2.39	1.96	n.d.	5.7
	15	2.43	1.78	n.d.	5.4
	20	2.38	1.77	n.d.	4.9
	Average + SD	2.4 ± 0.03	1.84 ± 0.10	—	5.3 ± 0.4

n.d.: not detected.

Fig. 2.

Average value of f as a function of electron energy (A) and film thickness (B). The data in (B) were recorded with 9.6 eV (present experiment) and 10 eV electrons (Rezaee et al.³³). The error bars represent standard deviations.

Fig. 2A shows that f remains fairly constant with energy. In contrast, it depends on film thickness as seen from Fig. 2B. Interestingly, the magnitude of f (i.e., h/λ) depends on the experiment (i.e., ours or that of Rezaee et al.), but not the variation with thickness. The change in magnitude probably reflects the slight differences in the lyophilisation procedure of the two groups. On the other hand, since the absolute CS must be the same from one film to another under similar conditions, it is possible to calculate the f of other similar LEE–DNA experiments based on the present f value. Furthermore, the invariance of f with electron energy should allow transforming effective CSs, recorded at other energies within the low-energy range, to absolute values.

Table 3 compares the CS data for DNA damage measured in the present study with those available in the literature from similar irradiation of dry plasmid DNA films; most of the latter have been measured only at 10 eV. We provide in the last column the average cross-section per nucleotide. These values assume that any electron coherence³⁹ and sequence-dependent⁴³ effects on the CS, average out for a 3197 base-pair DNA. The table also contains f calculated from eqn (5) using data from experiments performed with sufficiently thick films of DNA. From these f values, the reported CSs (σ_eff) are transformed into absolute CSs (σ). Within experimental error, the present CSs are in good agreement with those reported by Rezaee et al.,³³ who applied the same mathematical model. The values generated by the other authors,^27,44 which did not benefit from the model of Rezaee et al. in their analysis, produce absolute CSs of lower values, when we transform their σ_eff to σ. Panajotovic et al.²⁷ and Dumont et al.⁴⁴ measured only σ_eff for SSBs, which may also contribute to their lower value.

Table 3.

Present and previous CS data for DNA conformational damage induced by the impact of 9.6 and 10 eV electrons. f is the penetration factor applied to the measured effective CS to generate the absolute CS. σ represents the absolute CS per plasmid for LS. σ_n stands for the CS per nucleotide for LS, whose value arise essentially from strand breaks

Reference	Film medium	Film preparation method	Electron energy (eV)	Film thickness (nm)	f	σ (10−14 cm2)	σn (10−18 cm2)
This study	Plasmid DNA	Lyophilization	9.6	10	0.72 ± 0.15	5.1 ± 1.3	7.7 ± 2.1
				15	0.62 ± 0.18	5.1 ± 1.8	7.8 ± 2.8
				20	0.53 ± 0.19	5.0 ± 2.6	7.5 ± 4.0
Rezaee et al.33	Plasmid DNA	Lyophilization	10	10	0.6 ± 0.18	3.7 ± 1.4	5.8 ± 2.2
				15	0.5 ± 0.28	3.9 ± 1.5	6.1 ± 2.3
				20	0.4 ± 0.23	3.6 ± 1.4	5.6 ± 2.2
Panajotovic et al.27a	Plasmid DNA	Lyophilization	10	21	0.4 ± 0.2	2.7 ± 1.8	4.2 ± 2.6
Dumont et al.44	Plasmid DNA	Lyophilization	10	10	0.6 ± 0.1	1.5 ± 0.3	2.3 ± 0.5
Boulanouar et al.37b	Plasmid DNA	Self-assembly	10	8.8, 15.3, 19.8	0.73 ± 0.17	3.0 ± 0.3	4.8 ± 0.5

^aThe corrected CS recorded by Panajotovic et al. is for the formation of circular DNA, which contributes to more than 95% of loss of the supercoiled configuration.

^bThe statistical error for f is calculated based on the uncertainty in the average value of λ and film thickness.

The interaction of a LEE with a condensed molecule is affected by the neighboring molecules (e.g., via target polarization, diffraction and electron correlation)³⁹ and film morphology that may affect CS values. One expects different morphologies between the films in the experiment of Boulanouar et al.³⁷ and those in the others. In the former, the plasmid was different and stacked by intercalating Dap molecules. Thus, the similarity between CSs generated from the results of Boulanouar et al.,³⁷ the present ones and those of Rezaee et al.³³ suggests that film morphology is not a dominant factor contributing to the values of LEE-induced damage CS generated from multilayer duplex DNA films.

The CSs in Table 3 can also be compared to those recorded with single-stranded DNA under different film conditions. Cai et al.²⁸ measured strand break CSs for electron impact on self-assembled monolayer DNA films consisting of 50-base oligonucleotides. At energies of 8, 12 and 18 eV, they obtained values of 3.2, 17 and 28 × 10⁻¹⁸ cm² per nucleotide, respectively. The last two values, which are higher than those of Table 3 and Fig. 3, may indicate that single-stranded DNA is more vulnerable to LEE-induced damage than duplex DNA. Considering the relatively small number of nucleotides in the sample used by Cai et al., sequence dependence⁴³ may also influence their cross-section values. Much higher values are found for targets, which include the oligonucleotide and the supporting substrate. In that respect, Keller et al.⁴⁵ and Rackwitz et al.⁴⁶ obtained an average strand break CS of 4.8 × 10⁻¹⁵ cm² per nucleotide at 18 eV and 6.2 × 10⁻¹⁵ cm² per nucleotide at 10 eV, respectively, for a sub-monolayer of 13-mer oligonucleotide (5′-d(TT(ATA)₃TT)) fixed on an origami template; i.e., at least two orders of magnitude higher than the value from the experiment of Cai et al.,²⁸ in which electron collisions occurred away from the gold substrate.

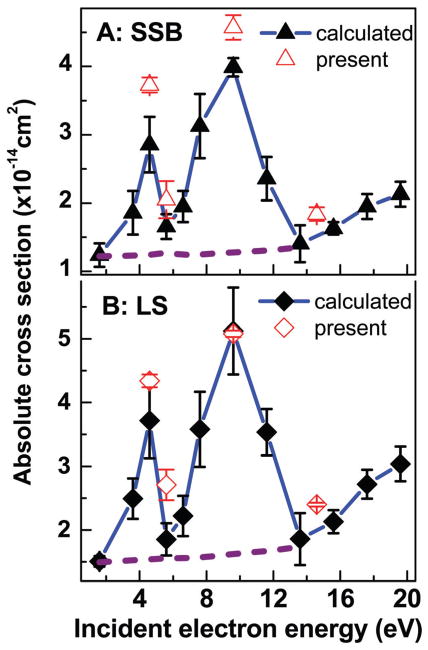
Fig. 3.

Absolute CSs for SSB (A) (solid triangles) and loss of the initial supercoiled configuration of DNA (B) (solid diamonds) induced by 2–20 eV electrons. The black points are the absolute values generated by using the effective yields of Luo et al.³⁴ The error bars are the standard deviations in their experiments. The penetration factor f of 0.29 obtained from transposing the present average f value from the dashed horizontal line in Fig. 2A to their results was used in the calculation. Open points are the average absolute CSs of the present study with the standard deviation given in Table 2.

C. Electron energy dependence of absolute CSs for DNA damage

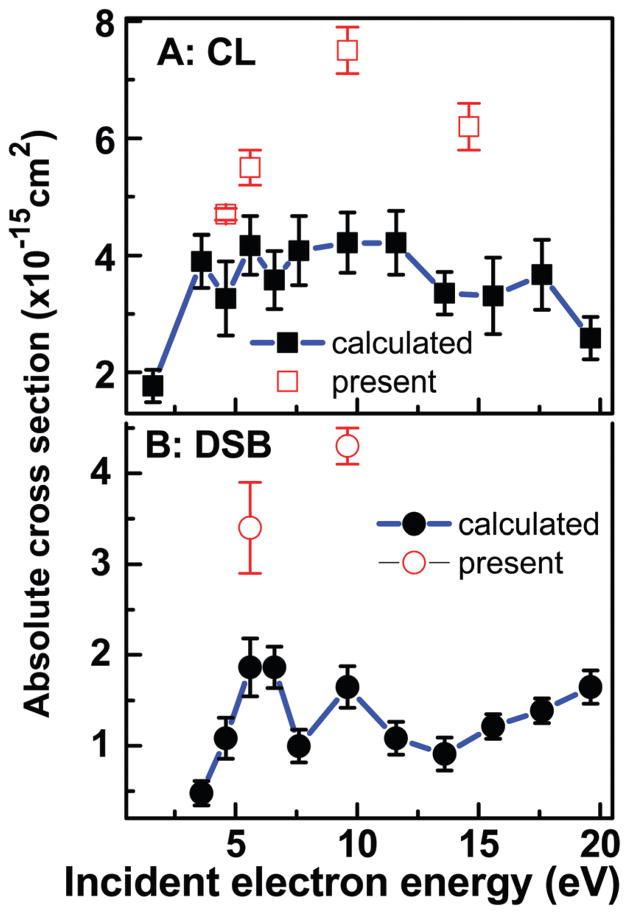
Luo et al. have reported the effective CSs for SSB, DSB, CL and LS induced by 2–20 eV in plasmid DNA.³⁴ These measurements were performed for films similar to those of the present experiments. Hence, according to preceding arguments, the present data could be used to generate absolute CSs over the 2–20 eV range from their results, as long as the assumption that f is independent of electron energy (Fig. 2A) remains valid. Here, we take the absolute value of σ_LS at 9.6 eV and the average f of 0.61 ± 0.13 found in the present experiments, to calculate the corresponding f in Luo et al. experiments (i.e., 0.29 ± 0.14). As far as σ_LS is concerned, the result shown in Fig. 3B is equivalent to simply calibrating the 2–20 eV LS curve of Luo et al. on our absolute CS at 9.6 eV. The other absolute CSs in Fig. 3A and 4 are produced via eqn (7) using f = 0.29 ± 0.14 and the effective CS of Luo et al.³⁴ The error bars are the standard deviations in their experiments. When the systematic percentage error on f is taken into account, the percentage errors on the CS values become much higher (e.g., those of Fig. 3B vary from 54 to 70%). As seen from Fig. 3, comparing the 2–20 eV CS with the present absolute values (open points) indicates that the approximation of a constant f over the 2–20 eV range works fairly well for σ_LS and σ_SSB. In similar comparisons in Fig. 4, larger deviations by factors of 1.5–1.8 and 1.7–2.4 are found between our absolute values of σ_CL and σ_DSB (open points), respectively, and those extrapolated from eqn (7) with the data from Luo et al.³⁴ For determining the contributions to this deviation arising from the errors in the measurements and those arising from the assumptions in the model of Rezaee et al. (and its extension from the invariance of f on energy), much more data points would have to be recorded on the yields of CL and DSB. Overall, the present results suggest the possibility to convert effective CSs to absolute values via the parameter f in the mathematic model of Rezaee et al.

Fig. 4.

Absolute CSs for CL and DSB (solid points) induced by 2–20 eV electrons generated from the effective yields of ref. 34 and the penetration factor f = 0.29 ± 0.14. The error bars are the standard deviations in the experiments of ref. 34. The open points are the average CSs of the present study with the standard deviations given in Table 2.

Interestingly, the CSs at the four electron energies investigated, particularly those at 4.6, and 9.6 eV, are only about twice lower than those at 100 eV.^47,48 100 eV electrons may cleave DNA by multiple events through non-resonant mechanisms including ionization, excitation and neutral dissociations.⁴⁹ The CS for the sum of the ionization and fragmentation channels at 100 eV is reported to be larger by one or two orders of magnitude than that at 10 eV for most organic molecules.^49,50 Therefore, it is expected that CSs of DNA SB at 100 eV should be much larger than those below 20 eV. According to previous studies 5, 6 and 10 eV electrons predominantly generate fragmentation in DNA by single events via the formation of transient core-excited anions decaying into dissociative neutral states and DEA.^21,26 Since 100 eV electrons have about the same thermalization distance as those of 10 eV,¹⁴ this comparison of the CS testifies the high efficiency (i.e., amount of damage per energy deposited) of LEEs to damage DNA. These results confirm quantitatively the previous suggestion²¹ that the formation of transient anions and DEA are more efficient processes than others to damage DNA.

V. Summary and conclusions

Films with thicknesses varying between 10 and 20 nm, made of lyophilized supercoiled DNA, were bombarded with electrons of 4.6, 5.6, 9.6 and 14.6 eV. The absolute CS at those energies for the loss of the initial supercoiled configuration (LS) and formation of SSB, DSB and CL were generated by applying the model of Rezaee et al.³³ to the yields measured near zero fluence. The CSs and attenuation lengths were shown to depend strongly on the thickness of the films. The crucial parameter of the model (i.e., the penetration factor f ) was found to be independent of the LEE energy within experimental errors. This invariance allowed determining the energy dependence of absolute CSs for these various types of DNA damage, over a wider range (2–20 eV), from previously measured effective CSs. The CS to produce SSB is smaller, but similar to that of LS, indicating that SSB are the main conformational damage. The CS for DSB and CL are about one order of magnitude smaller than those of LS and SSB. The results corroborate quantitatively previous measurements indicating that LEEs are highly efficient to induce conformational DNA damage.

The good agreement of present results with the transformed values from previous measurements suggests that it is possible to convert effective CSs to absolute CSs via the parameter f in the mathematic model of Rezaee et al.³³ Considering the amount of work required to generate absolute CSs, the present method appears highly efficient to produce such CSs over a wide energy range. The present comprehensive study suggests that a similar procedure could be adapted to obtain absolute CSs for electron-induced damage/reaction occurring in other molecular or biomolecular solids. Similar studies are presently underway with the chemotherapeutic agent cisplatin bound to plasmid DNA, to transform the LEE energy dependence of effective CSs for damage to the cisplatin–DNA complex⁵¹ to absolute CSs. The latter are expected to be of considerable value to estimate the increase in the local dose distribution near the DNA of cancer cells in patients receiving concomitant radio-and chemo-therapy.