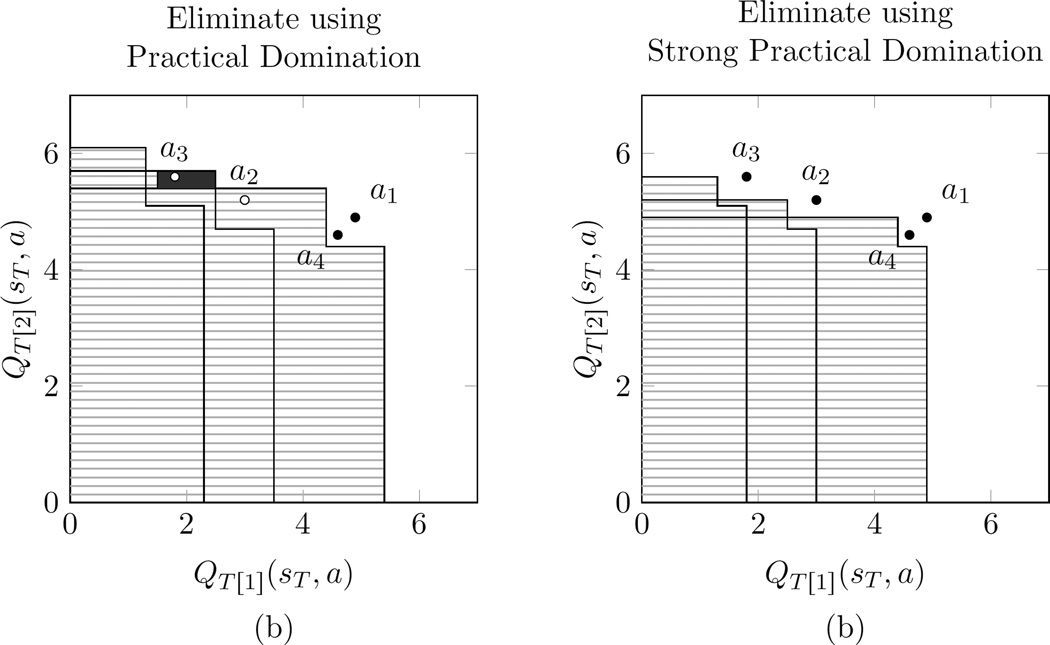
Figure 4.

Comparison of rules for eliminating actions. In this simple example, we suppose the Q-vectors (Q_T[1] (s_T, a), Q_T[2] (s_T, a)) are (4.9, 4.9), (3, 5.2), (1.8, 5.6), (4.6, 4.6) for a₁, a₂, a₃, a₄, respectively, and suppose Δ₁ = Δ₂ = 0.5. Figure 4(a): Using the Practical Domination rule, action a₄ is not eliminated by a₃ because it is not much worse according to either basis reward, as judged by Δ₁ and Δ₂. Action a₂ is eliminated because although it is slightly better than a₁ according to basis reward 2, it is much worse according to basis reward 1. Similarly, a₃ is eliminated by a₂. Note the small solid rectangle to the left of a₂: points in this region (including a₃) are dominated by a₂, but not by a₁. This illustrates the non-transitivity of the Practical Domination relation, and in turn shows that it is not a partial order. Figure 4(b): Using Strong Practical Domination, which is a partial order, no actions are eliminated, and there are no regions of non-transitivity.