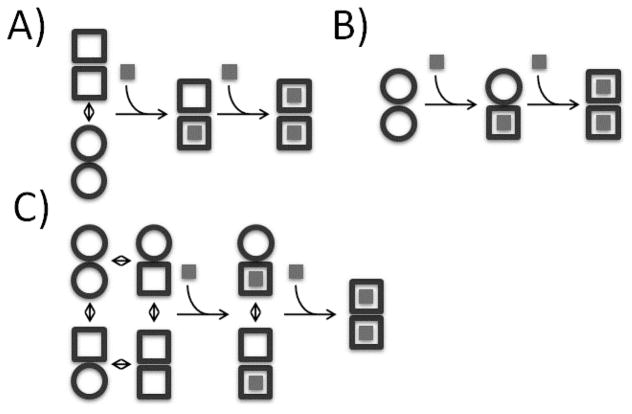
Figure 1.

Schematic representation of homotropic allosteric models for a dimeric protein. ○ and □ correspond to subunits in binding-incompetent, and binding-competent states, respectively. (A) Monod-Wyman-Changeux (MWC): The symmetry of the dimer is preserved, so that only ○○ and □□ states are permitted. In the absence of ligand, both states are populated, while ligand binding forces the dimer into the □□ state. If the initial equilibrium favors the ○○ state, binding is positively cooperative, since the energetic cost of the ○○ to □□ transition is paid by binding the first, but not the second ligand. Note that in the standard MWC model, both ○○ and □□ bind ligand, but with different affinities. For the sake of simplicity we have shown the limiting case where ○○ is binding-incompetent. (B) Koshland-Nemethy-Filmer (KNF): Each subunit converts from the ○ to the □ state only upon binding ligand. Cooperativity is explained in terms of the strengths subunit-subunit interactions. If the transition from the ○○ to ○□ interface is energetically more favorable than from the ○□ to □□, binding is negatively cooperative, and the first ligand is bound more strongly than the second. If the transition from the ○○ to ○□ interface is less favorable than from the ○□ to □□, binding is positively cooperative, and the second ligand is bound more strongly than the first. (C) Energy allosteric model (EAM): Each unbound subunit can populate either the ○ or □ state, and the equilibrium of each subunit is influenced by the state of the adjacent subunit. If the binding competent (□) state of one subunit stabilizes the □ state of the adjacent subunit, binding is positively cooperative. Conversely, if the binding competent □ state of one subunit stabilizes the binding-incompetent ○ state of the adjacent subunit, binding is negatively cooperative. Adapted from Freiburger et al [23]