Figure 2.
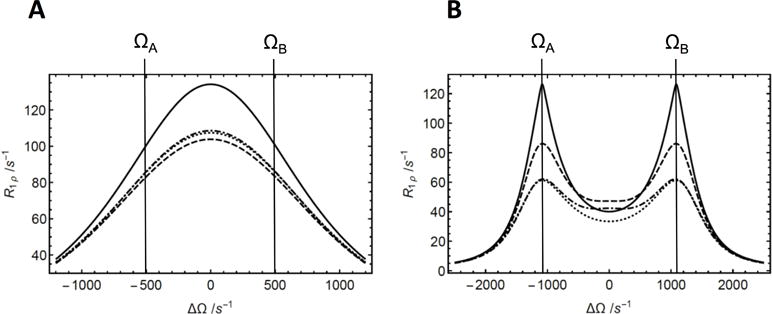
Approximations of R1ρ for two-site chemical exchange. (a) (Solid) Numerical calculation of the least negative real eigenvalue of the 6 × 6 evolution matrix, (dashed) calculation from the first-order (in) approximation, based on L + K + R (Eq. 8); (dotted) calculation from the first-order (in) approximation, based on L + K + R, and truncated to first order in R (Eq. 10), as also previously provided by Trott and Palmer [10] and Baldwin and Kay [11]; (dashed-dotted) calculation from the first-order approximation, based on L + K (Eq. 14). Parameters used for the calculations were R1 = 1.5 s−1, R2 = 11 s−1, pA = 0.5, pB = 0.5, ω1 = 1000 s−1, ΩB − ΩA = 1000 s−1, and kex = k12 + k21 = 1000 s−1. (b) (solid) Numerical calculation of the least negative real eigenvalue of the 6 × 6 evolution matrix; (dashed) calculation from the second-order approximation from Eqs. 14, 25 and 29; (dotted) calculation from the first-order (in) approximation, based on L + K + R (Eq. 8); (dashed-dotted) calculation from the first-order approximation, based on L + K (Eq. 14). Parameters used for the calculations were R1 = 1.5 s−1, R2 = 11 s−1, pA = 0.5, pB = 0.5, ω1 = 500 s−1, ΩB − ΩA = 2400 s−1, and kex = k12 + k21 = 250 s−1.
