Figure 5.
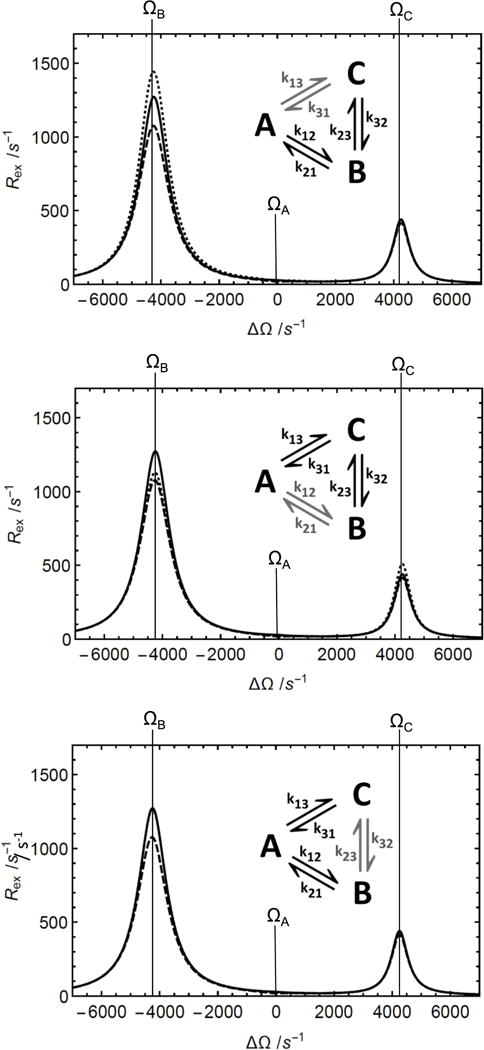
The Woodbury approximation of the Rex contribution to R1ρ in the triangular three-state chemical exchange situation depends on how the linear fragment for the approximation is chosen. (Solid) Numerical solution of Rex = −λ/sin2θ from the least negative real eigenvalue of the 9 × 9 evolution matrix, (dashed) first-order approximation (Eq. 11) and (dotted) Woodbury approximation (Eq. 50). To center the graph, parameters were chosen so that δA = ΔΩ. Parameters used for all calculations were pA = 0.9, pB = 0.05, pC = 0.05, k12 +k21 = 500 s−1, k13+k31 = 50 s−1, k23+k32 = 20 s−1, ω1= 350 s−1, ΩB − ΩA = 4250 s−1, and ΩC − ΩA = −4250 s−1. The kinetic scheme is shown in each panel (black: linear fragment; grey: non-linear fragment). Linear fragments are (top) A-B-C, (middle) A-C-B, (bottom) C-A-B. The Woodbury approximation fits best when the slowest exchange process is chosen as the nonlinear fragment.
