Conservation of coevolving protein interfaces bridges prokaryote–eukaryote homologies in the twilight zone

Significance

Interacting proteins tend to coevolve through interdependent changes at the interaction interface. This phenomenon leads to patterns of coordinated mutations that can be exploited to systematically predict contacts between interacting proteins in prokaryotes. We explore the hypothesis that coevolving contacts at protein interfaces are preferentially conserved through long evolutionary periods. We demonstrate that coevolving residues in prokaryotes identify interprotein contacts that are particularly well conserved in the corresponding structure of their eukaryotic homologues. Therefore, these contacts have likely been important to maintain protein–protein interactions during evolution. We show that this property can be used to reliably predict interacting residues between eukaryotic proteins with homologues in prokaryotes even if they are very distantly related in sequence.

Abstract

Protein–protein interactions are fundamental for the proper functioning of the cell. As a result, protein interaction surfaces are subject to strong evolutionary constraints. Recent developments have shown that residue coevolution provides accurate predictions of heterodimeric protein interfaces from sequence information. So far these approaches have been limited to the analysis of families of prokaryotic complexes for which large multiple sequence alignments of homologous sequences can be compiled. We explore the hypothesis that coevolution points to structurally conserved contacts at protein–protein interfaces, which can be reliably projected to homologous complexes with distantly related sequences. We introduce a domain-centered protocol to study the interplay between residue coevolution and structural conservation of protein–protein interfaces. We show that sequence-based coevolutionary analysis systematically identifies residue contacts at prokaryotic interfaces that are structurally conserved at the interface of their eukaryotic counterparts. In turn, this allows the prediction of conserved contacts at eukaryotic protein–protein interfaces with high confidence using solely mutational patterns extracted from prokaryotic genomes. Even in the context of high divergence in sequence (the twilight zone), where standard homology modeling of protein complexes is unreliable, our approach provides sequence-based accurate information about specific details of protein interactions at the residue level. Selected examples of the application of prokaryotic coevolutionary analysis to the prediction of eukaryotic interfaces further illustrate the potential of this approach.

Cells function as a remarkably synchronized orchestra of finely tuned molecular interactions, and establishing this molecular network has become a major goal of molecular biology. Important methodological and technical advances have led to the identification of a large number of novel protein–protein interactions and to major contributions to our understanding of the functioning of cells and organisms (1, 2). In contrast, and despite relevant advances in EM (3) and crystallography (4), the molecular details of a large number of interactions remain unknown.

When experimental structural data are absent or incomplete, template-based homology modeling of protein complexes represents the most reliable option (5, 6). Similarly to modeling of tertiary structure for single-chain proteins, homology modeling of protein–protein interactions follows a conservation-based approach, in which the quaternary structure of one or more experimentally solved complexes with enough sequence similarity to a target complex (the templates) is projected onto the target. Template-based techniques have provided models for a large number of protein complexes with structurally solved homologous complexes (7–10). Unfortunately, proteins involved in homologous protein dimers tend to systematically preserve their interaction mode only for sequence identities above 30–40% (11). For larger divergences, defining the so-called twilight zone (11, 12), it is not possible to discriminate between complexes having similar or different quaternary structures (11, 13, 14). As a consequence, the quality of the final models strongly depends on the degree of sequence divergence between the target and the available templates.

In contrast to more traditional approaches based on homology detection and sequence conservation, contact prediction supported by residue coevolution (15–25) makes use of sequence variability as an alternative source of information (26). The analysis of residue coevolution has been successfully applied to contact prediction at the interface of protein dimers (27–33), eventually leading to de novo prediction of protein complexes assisted by coevolution (29, 30). In these methods, coevolutionary signals are statistically inferred from the mutational patterns in multiple sequence alignments of interacting proteins. Coevolution-based methods have been shown to be highly reliable predictors of physical contacts in heterodimers, when applied to large protein families with hundreds of nonredundant pairs of interacting proteins (28–30, 34, 35). Unfortunately, these methods cannot be straightforwardly applied to the analysis of eukaryotic complexes where paralogues are abundant, making it very difficult to distinguish their interaction specificities. In consequence, many eukaryotic complexes remain out of reach for both template-based homology modeling (14) and coevolution-guided reconstruction. To address this eukaryotic “blind spot” it is essential to identify long-standing evolutionary constraints that could be used for guiding the reliable projection of structural information from remote homologs.

We test the hypothesis that strong coevolutionary signals identify highly conserved protein–protein contacts, making them particularly adequate for homology-based projections. From a structural modeling point of view, we test whether and when coevolution-based contact predictions can be projected to homologous complexes. In particular, we focus on the paradigmatic problem of contact prediction in eukaryotic complexes based on coevolutionary signals detected in distant alignments of prokaryotic sequences. To this aim, we develop a domain-centered protocol to detect coevolving residues in multiple sequence alignments of prokaryotic complexes and evaluate their accuracy in predicting interprotein contacts in eukaryotes. Our results show that when the signal of coevolution in prokaryotic alignments is strong, conserved interprotein contacts in eukaryotes can be reliably predicted solely using prokaryotic sequence information. These results provide the basis for the application of coevolution to assist de novo structure prediction of eukaryotic complexes with homologs in prokaryotes even when they are highly divergent in sequence, a scenario where standard template-based homology modeling is unfeasible or unreliable.

Results

Benchmark Dataset to Study the Interplay Between Coevolution and Structural Conservation at Protein Interfaces.

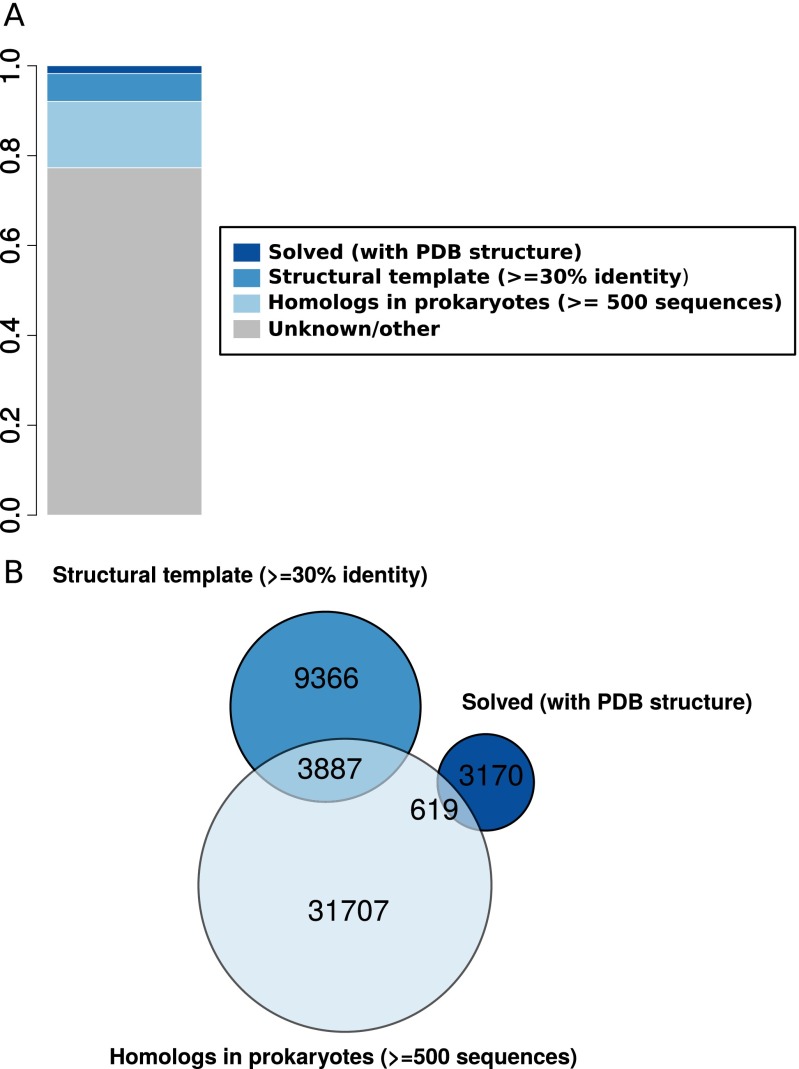
An initial analysis of the human interactome (SI Text and Fig. S1) reveals that for ∼17% of human protein–protein interactions each interaction partner shares homology with many prokaryotic sequences. Most of these interactions lack reliable structural information. In the following, we propose that interprotein coevolution based on large collections of prokaryote sequences can be an invaluable source of information about those, otherwise unsolved, protein–protein interaction interfaces.

Fig. S1.

(A) Proportion of pairs of proteins in the human protein–protein interaction network [214,806 heterodimeric interactions retrieved from BIOGRID (64)] containing interprotein domain interactions with solved structure (dark blue), having reliable structural templates (≥30% sequence identity, blue), with more than 500 prokaryotic nonredundant homologs (<80% sequence identity), and lacking an experimental structure or a reliable structural template (light blue). (B) Venn diagram for the three sets of human interactions with structural or evolutionary information.

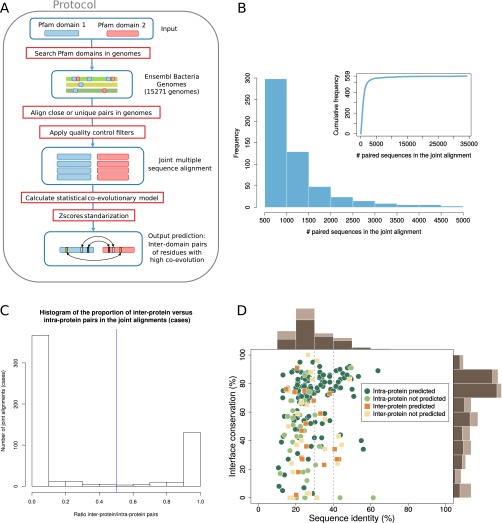
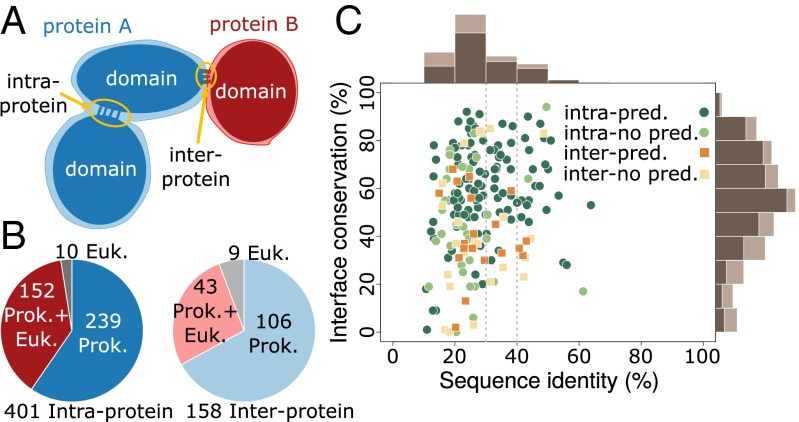
To investigate the relevance of coevolution in the structural conservation at protein–protein interfaces among highly divergent homologs, we created a dataset of prokaryotic and eukaryotic domain–domain interfaces that integrates structural and coevolutionary data at the residue level. We started from the complete dataset of heterodimeric Pfam (36) domain–domain interactions with known 3D structure (37). Coevolutionary analysis of a protein interface requires a large set of paired sequences from the families of two interacting proteins in the complex (28–30). Distant evolutionary relationships can be often unveiled only at the level of domains (38); therefore, we devised a domain-centered protocol that enables the detection and the alignment of many conserved families of interacting domains (Materials and Methods and Fig. S2A). We searched for homologous sequences of the interacting domains in 15,271 prokaryotic genomes and built a joint alignment by pairing domains in genomic proximity (29, 30). We used proximity in the genome to identify the existence of a specific physical interaction between two domains (39). This protocol retrieved 559 cases of domain–domain pairs (each corresponding to a unique Pfam family–family pair) having 3D structural evidence of interaction in at least one prokaryotic or eukaryotic species and containing more than 500 sequences in the corresponding (nonredundant) joint alignment (Fig. 1B and Fig. S2B). For every domain–domain pair in this set, we computed coevolutionary z-scores for all of the interdomain residue–residue pairs that quantify the direct mutual influence between two residues (28) in different domains. Finally, we obtained the set of coevolving interdomain pairs of residues by retaining those pairs for which a strong coevolutionary signal was detected (Materials and Methods). We classified each domain–domain interface as intra- or interprotein (Fig. 1A) if the majority of paired sequences are codified within the same or different genes, respectively; 401 out of 559 domain pairs were classified as intraprotein and 158 as interprotein (Fig. 1B and Fig. S2C).

Fig. S2.

(A) Scheme of the coevolutionary protocol developed. (B) Frequency distribution of the number of paired sequences in the joint alignments in the range of 500–5,000 sequences. (Inset) Cumulative frequency distribution for the whole range of number of paired sequences in the joint alignments. (C) Histogram of the ratio of interprotein to intraprotein pairs in the joint alignments. Cases of ambiguous classifications are rare: In 493 out of 559 cases, the paired sequences are predominantly (more than 90% of the pairs) found either in the same gene or in different genes. We classified a case as intra- or interprotein when the ratio was lower or higher than 0.5, respectively. (D) Percentages of interface conservation and sequence identities for the 152 intraprotein and 43 interprotein cases using representative interfaces. Interface conservation and sequence similarity were defined as described in Fig. 1. Marginal histograms computed on the whole set of cases are in light brown; marginal histograms for predicted cases are in dark brown.

Fig. 1.

Summary of the coevolutionary/structural dataset generated by our protocol. (A) The two kinds of domain–domain interactions discussed in the text: In intraprotein cases the two domains are codified within the same gene; in interprotein cases they are found in different genes. (B) Dataset composition according to inter- or intraprotein classification and the availability of 3D structure in prokaryotes and eukaryotes. (C) Percentages of interface conservation and sequence identities for 152 intraprotein cases and 43 interprotein cases. Interface conservation was calculated as the proportion of contacts in prokaryotic interfaces that are also in contact in eukaryotes. Sequence identities were calculated as the proportion of identical amino acids between the best aligned prokaryotic PDB sequence and the best aligned eukaryotic PDB sequence (SI Text). A domain–domain interaction was labeled as predicted when at least an interdomain pair of residues was classified as coevolving (Materials and Methods). Marginal histograms computed on the whole set of cases are in light brown; marginal histograms for predicted cases are in dark brown.

We first classified every 3D structure for each domain–domain interaction as prokaryotic or eukaryotic (SI Text). To deal with conformational variability in the available experimental structures, we used two different definitions for the set of contacts forming each domain–domain interface (Materials and Methods). First, we defined a comprehensive interface by merging all of the interdomain contacts (defined as residues closer than 8 Å) extracted from all known homologous structures. This definition incorporates information from different biological (e.g., conformational changes) and methodological scenarios. Second, we selected the complex that best aligns to the Pfam profile and defined the corresponding contacts as the representative interface. A comprehensive and a representative interface were computed separately for each domain–domain pair and for both eukaryotic and prokaryotic structures. When not specified otherwise, we will refer to the results obtained from the analysis of comprehensive interfaces; however, all of the analyses were performed in parallel for the representative complexes with similar results. All of the collected data were integrated in a dataset (Fig. 1) of 559 domain interactions with their interdomain coevolving residues and their corresponding prokaryotic and/or eukaryotic structural interfaces.

Our dataset includes 43 interprotein and 152 intraprotein cases (Fig. 1B) with structure in both prokaryotes and eukaryotes. For these cases, we quantified the structural interface conservation as the proportion of prokaryotic contacts that are also in contact in their homologous sites in eukaryotes. In this subset, 66% (129 out of 195) of the cases correspond to sequence identities below 30%. Complexes with sequence identities below 30–40% have highly variable values of interface conservation, and conserved interfaces cannot be identified using sequence identity alone (see Fig. 1C and Fig. S2D for representative interfaces). This variability reflects the difficulties associated to accurate template-based homology modeling in the twilight zone. In our dataset, a naive extrapolation of contacts from prokaryotes to eukaryotes would result in highly unreliable predictions, due to the large divergences. This set of homologous interfaces provides the basis for investigating the structural conservation of coevolving residues between prokaryotic and eukaryotic interfaces even at large sequence distances.

Coevolving Residues Identify Structurally Conserved Contacts at Protein Interfaces.

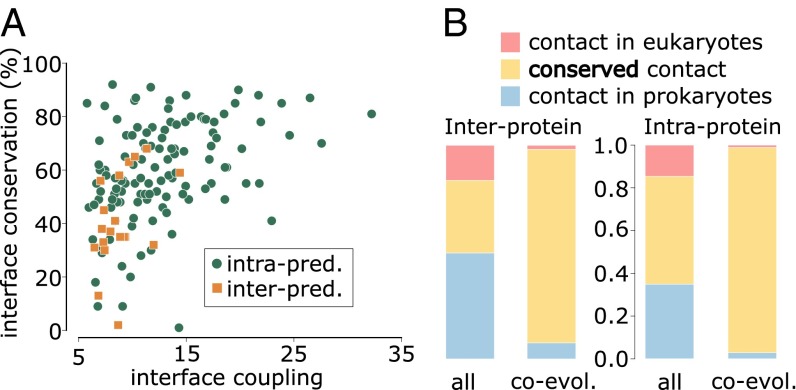
We detected strong coevolutionary signals in 20 out of 43 interprotein cases (and in 121 out of 152 intraprotein cases). The proportion of cases with predictions (strong coevolutionary signals) is higher when the structural interface conservation is larger (Fig. 1C). This suggests that coevolution is indicative of a greater structural conservation. To gain further insight, we studied the relationship between structural interface conservation and the degree of coevolution detected in each case. To this aim, we calculated a score, called interface coupling, by averaging the z-score of the five strongest interdomain coevolving pairs (33). As shown in Fig. 2A, the level of interface coupling determines a lower bound for interface conservation (i.e., the stronger the interface coupling, the higher the minimal interface conservation observed in our dataset). Moreover, large interface coupling values consistently identify domain–domain pairs that interact via a single 3D interaction topology (SI Text), suggesting that a single, conserved interface may be an important factor in explaining strong domain–domain coevolution.

Fig. 2.

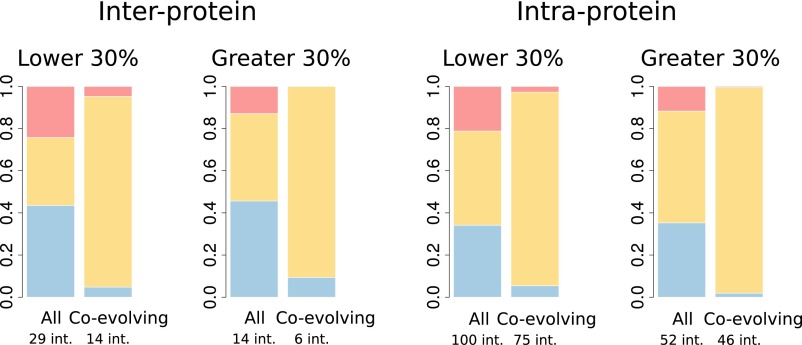
(A) Relation between interface structural conservation (defined as in Fig. 1) and interface coupling (the average z-score of the five strongest interdomain coevolving pairs) for 20 interprotein and 121 intraprotein domain–domain interactions with contact predictions (i.e., strong coevolutionary signals) and structurally solved prokaryotic and eukaryotic homologous complexes. (B) Proportion of conserved contacts at the homologous sites of prokaryotic/eukaryotic complexes, computed from the total set of contacts and the subset of coevolving contacts, and for inter- and intraprotein cases. Blue: contacts found in a prokaryotic complex and not in the homologous eukaryotic complex. Red: contacts found in a eukaryotic complex and not present in the homologous prokaryotic complex. Yellow: contacts shared by prokaryotic and eukaryotic complexes. Forty-eight out of 52 coevolving contacts in interprotein complexes and 1,039 out of 1,070 coevolving contacts in intraprotein complexes are shared by prokaryotes and eukaryotes.

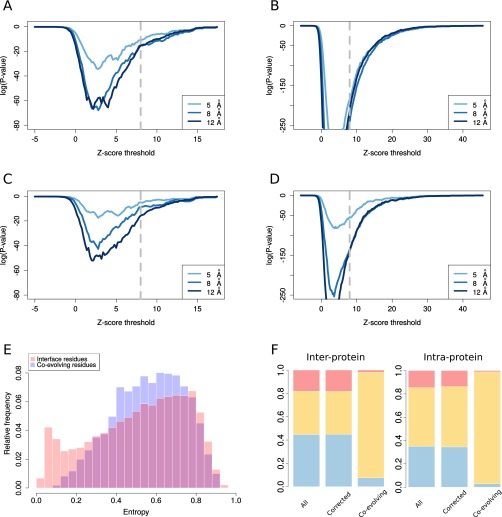
A comparison between homologous sites in eukaryotic and prokaryotic structures clearly reveals that pairs of residues that are coevolving and in contact in prokaryotes (interprotein: 52 contacts out of 56 coevolving pairs; intraprotein: 1,070 contacts out of 1,107 coevolving pairs) are systematically found in contact in the 3D structures of the corresponding eukaryotic homologs (Fig. 2B). This effect is highly significant compared with the proportion of prokaryotic contacts shared with a eukaryotic homolog expected by chance (P < 10⁻¹⁰, one-tailed Fisher exact test for both interprotein and intraprotein cases; SI Text) and it is robust to different definitions of coevolution and contacts (Fig. S3 A and B). The analysis of representative interfaces leads to the same conclusion (Fig. S3 C and D). Moreover, the structural conservation of coevolving contacts is much higher than expected by chance after considering the conservation in sequence of the coevolving residues (SI Text and Fig. S3 E and F). Remarkably, focusing on the difficult cases in the twilight zone (less than 30% sequence identities, 29 interprotein and 100 intraprotein) we also found a highly significant enrichment in conserved coevolving contacts (Fig. S4, P < 10⁻⁶, one-tailed Fisher exact test for both interprotein and intraprotein cases, and SI Text).

Fig. S3.

(A and B) One-tailed Fisher test P value (SI Text) as a function of the z-score threshold (all coevolving pairs with a z-score greater than the z-score threshold are considered) using comprehensive interfaces, for interprotein (A) and intraprotein (B) cases. (C and D) One-tailed Fisher test P value (SI Text) as a function of the z-score threshold using representative interfaces, for interprotein (C) and intraprotein (D) cases. (E) Probability distributions for the entropy of positions in sequence alignments corresponding to two different sets of residues: interface residues (residues involved in domain–domain contact, red) and coevolving residues (residues involved in a coevolving pair, blue). The entropy of each position is calculated from the corresponding column in the joint multiple sequence alignments. (F) Proportion of conserved contacts at the homologous sites of prokaryotic/eukaryotic complexes, as computed from the total set of contacts (All), from a corrected set having the same entropy distribution of the subset of coevolving contacts (Corrected, SI Text), and from the subset of coevolving contacts (Co-evolving), both for interprotein (Left) and intraprotein (Right) cases. In blue: proportion of contacts found in a prokaryotic complex and not in the homologous eukaryotic complex. In red: proportion of contacts found in a eukaryotic complex and not present in the homologous prokaryotic complex. In yellow: proportion of contacts shared by prokaryotic and eukaryotic complexes.

Fig. S4.

Proportion of contacts found only in prokaryotes, only in eukaryotes, or conserved for all of the contacts and for coevolving contact. The cases are divided into two groups depending on whether the percentage of sequence identity (Materials and Methods) between prokaryotic and eukaryotic representative complexes is lower or greater than 30%.

In detail, the proportion of interprotein contacts conserved in prokaryotic and eukaryotic interfaces (37%) increases up to 91% (48 conserved contacts out of 53 coevolving pairs in contact in prokaryotes or eukaryotes) for pairs of coevolving residues (Fig. 2B). Interestingly, three out of the four coevolving pairs that apparently are not conserved correspond to residue pairs that are spatially close in the eukaryotic structure (less than 10 Å). For the cases in the twilight zone, 23 out of 25 coevolving contacts are conserved and one of the remaining pairs is at 8.1 Å in eukaryotes. Intraprotein interfaces follow the same trend: The proportion of conserved contacts goes from 50 to 96% for coevolving pairs (Fig. 2B; 1,039 conserved contacts out of 1,082 coevolving contacts). Again, we found that coevolving contacts are highly conserved even for interfaces in the twilight zone (583 conserved out of 615). These results are robust to the specific measure of sequence divergence (SI Text and Fig. S5). They clearly prove that coevolving contacts have been preferentially conserved during the course of evolution, validating our hypothesis that coevolution identifies structurally conserved contacts. Moreover, when applied to coevolving pairs of residues at prokaryotic interfaces, this property should allow one to predict interface contacts in eukaryotic proteins, in a wide range of evolutionary distances, including the twilight zone.

Fig. S5.

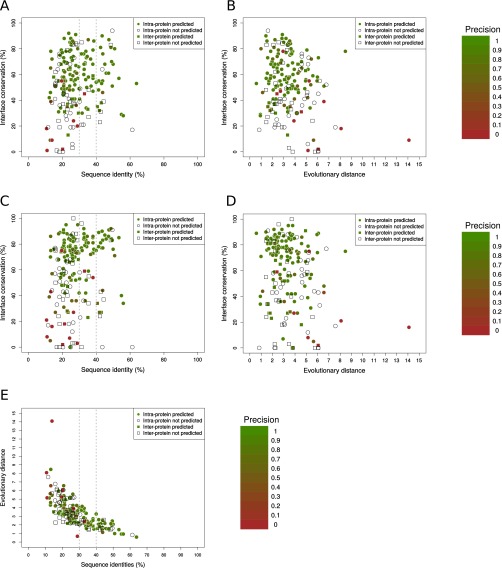
Each point represents a domain–domain interaction (interprotein in squares, intraprotein in circles) with structure in both prokaryotes and eukaryotes, colored by its contact prediction precision (white when there are not predictions). Percentages of sequence identity between the prokaryotic and eukaryotic representative complexes and interface conservation (SI Text) are also shown. (A) Precision by case in eukaryotes as a function of the percentage of sequence identity and interface conservation using contacts from the comprehensive interfaces. (B) Precision by case in eukaryotes as a function the evolutionary distance and interface conservation using contacts from representative interfaces. (C) Precision by case in eukaryotes as a function of the percentage of sequence identity and interface conservation using contacts from comprehensive interfaces. (D) Precision by case in eukaryotes as a function of the evolutionary distance and interface conservation using contacts from representative interfaces. (E) Evolutionary distances versus sequence identity plot. Each point corresponds to a domain–domain pair having both a prokaryotic and a eukaryotic experimentally solved structure. (188 cases, Spearman’s correlation = −0.79; SI Text).

Contact Prediction at Eukaryotic Protein Interfaces.

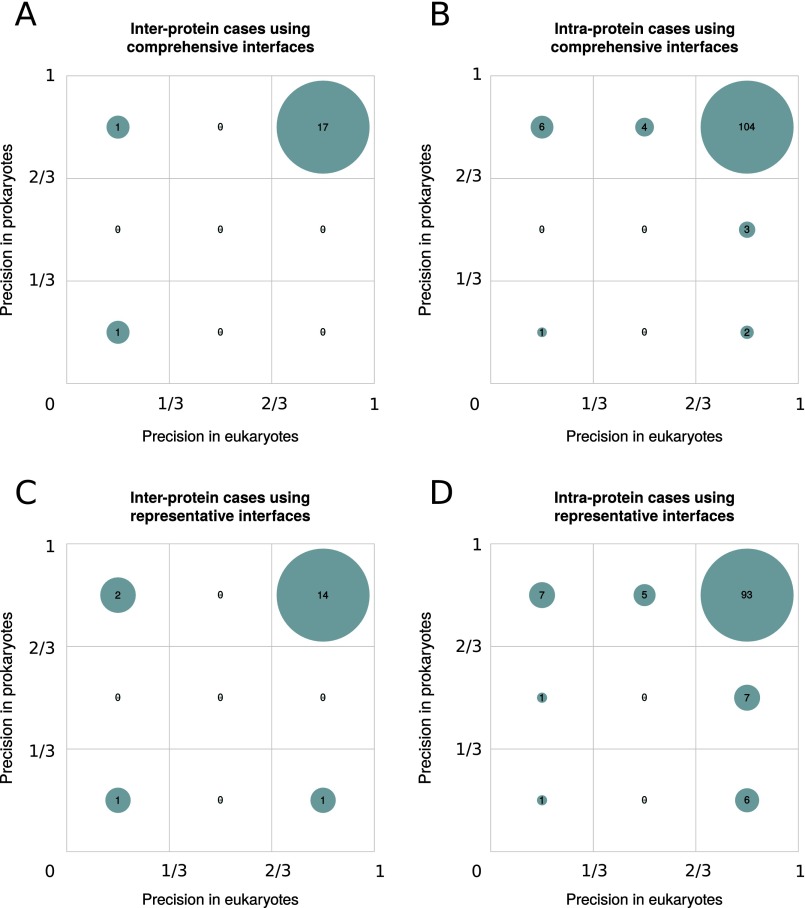
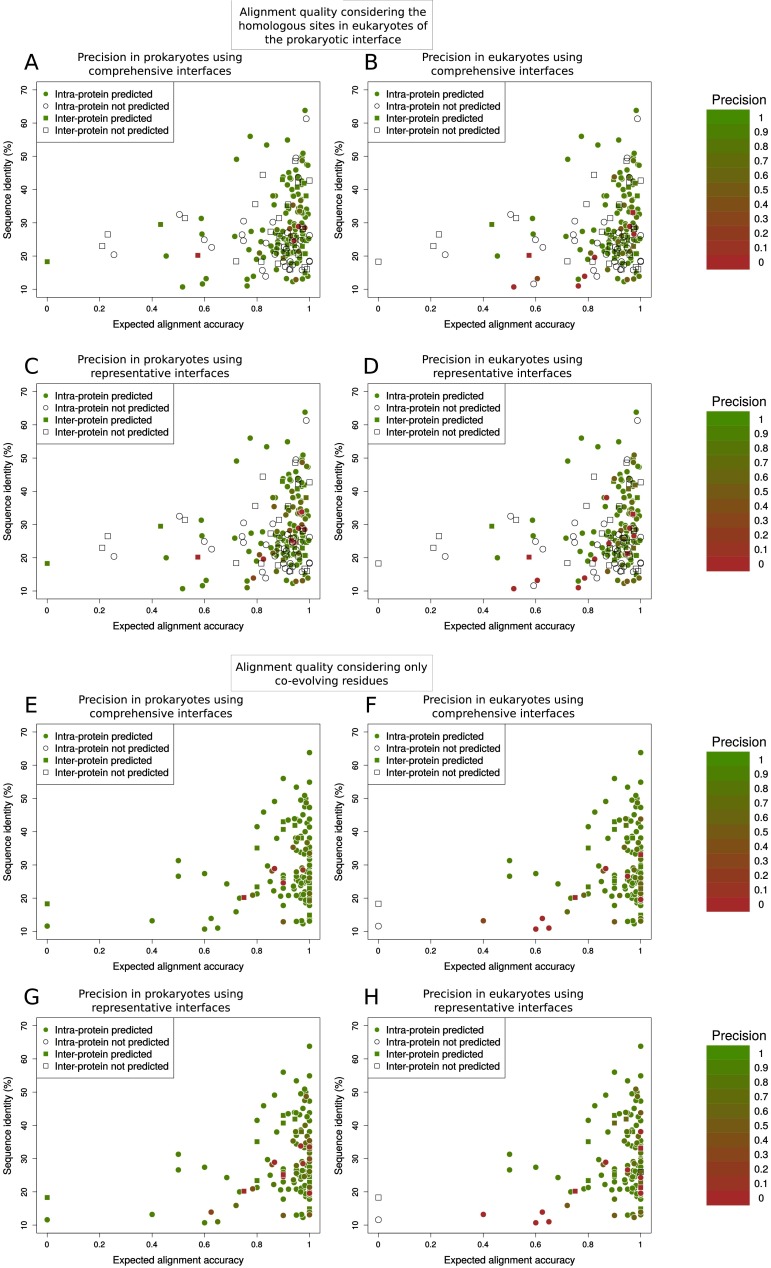
We assessed the precision of prokaryotic coevolving pairs in predicting contacts in prokaryotic and eukaryotic structures for cases with predictions in structurally solved regions, both in prokaryotic and eukaryotic interfaces (19 interprotein and 120 intraprotein). The vast majority of these cases have a high precision in the two superkingdoms (Fig. S6). Only 1 out of 19 interprotein cases in prokaryotes (6 out of 120 in intraprotein) was predicted with a precision lower than 0.6 (Fig. S6). For eukaryotes, these numbers are only slightly higher with 2 out of 19 interprotein (11 out of 120 in intraprotein; Fig. S6). The few additional cases with low precision found for representative interfaces are evenly distributed in prokaryotes and eukaryotes, suggesting that they are not related with the projection procedure (Fig. S6). Most false positives occur in cases within the twilight zone with low structural interface conservation (Fig. S5 A and C). This low structural conservation could result in poorly aligned eukaryotic sequences. We evaluated the impact of alignment quality on the projection of contact predictions from prokaryotes to eukaryotes by computing the averaged expected alignment accuracy for residues at the eukaryotic homologous sites of the prokaryotic interface (SI Text). Indeed, most of the cases with low-quality predictions in eukaryotes but not in prokaryotes correspond to low-quality sequence alignments, both for comprehensive (Fig. S7 A and B) and representative interfaces (Fig. S7 C and D).

Fig. S6.

Precision comparison of contact predictions between prokaryotic and eukaryotic interfaces with 3D structures in both superkingdoms. (A) Relative frequency of interprotein interfaces in three intervals of precision in both prokaryotes and eukaryotes using comprehensive interfaces. (B) Relative frequency of prokaryotic and eukaryotic precisions of intraprotein interfaces using comprehensive interfaces. (C) Relative frequency of prokaryotic and eukaryotic precisions for interprotein interfaces using representative interfaces. (D) Relative frequency of prokaryotic and eukaryotic precisions for intraprotein interfaces using representative interfaces.

Fig. S7.

Quality alignment influence on the transference from prokaryotes to eukaryotes. Each point represents a domain–domain interaction (interprotein in squares, intraprotein in circles) with structure in both prokaryotes and eukaryotes, colored by its contact prediction precision (white when there are not predictions). Percentage of sequence identity between the prokaryotic and eukaryotic representative complexes and expected alignment accuracy (see SI Text, Alignment Quality Measurement) are also shown. (A–D) The alignment quality has been computed considering the homologous sites in the eukaryotic sequences of the comprehensive prokaryotic interface for comprehensive (A and B) and representative (C and D) interfaces. (E–H) The alignment quality has been computed considering only coevolving residues (see SI Text, Alignment Quality Measurement) for comprehensive (E and F) and representative interfaces (G and H).

As discussed above, the high reliability of coevolution as a predictor of contacts in prokaryotes and the preferential conservation of coevolving contacts allows one to predict contacts in eukaryotes without any prior structural information. To further assess this point, we quantified the quality of eukaryotic contact prediction for all cases in which a eukaryotic structure was available to check the resulting predictions (51 interprotein and 162 intraprotein; Fig. 1B). We detected 62 coevolving pairs in 22 interprotein cases (approximately three predictions per case) and 1,140 pairs in 124 intraprotein cases (approximately nine per case). We found that the precision in eukaryotes is very high both in interprotein (precision = 0.81, Fig. 3A) and in intraprotein cases (precision = 0.95, Fig. 3B) and it is only slightly lower than the precision obtained in prokaryotes (Fig. 3 C and D; precision interprotein = 0.86 and precision intraprotein = 0.95). We repeated the analysis after removing cases with low alignment quality, using a filter based on the pairs of coevolving residues (SI Text). In line with the discussion in the previous paragraph, the results suggest that an a priori filter can detect cases in which projected predictions have a lower precision (Fig. S7 E and F and Table S1).

Fig. 3.

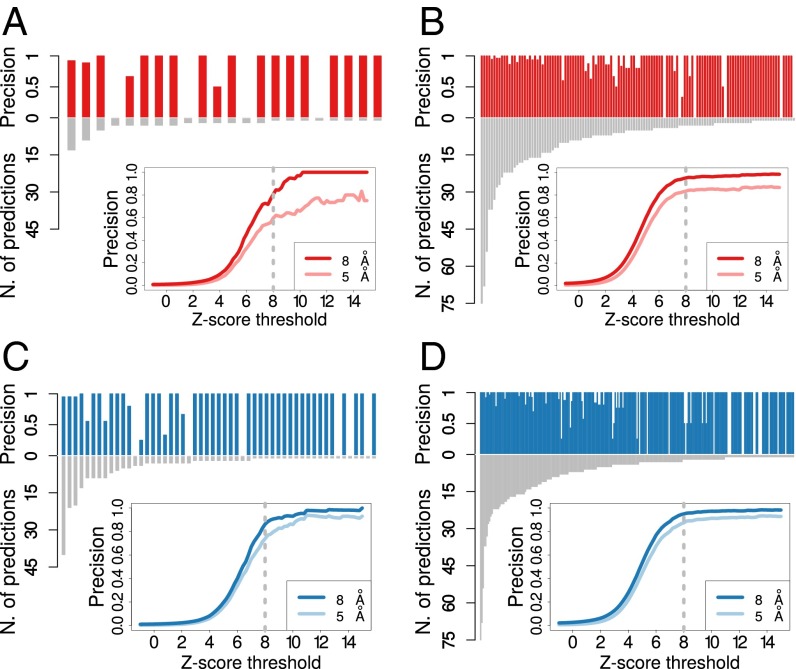
Precision and number of predictions for each of the 22 interprotein (A) and 124 intraprotein (B) domain–domain interfaces in eukaryotes with at least one detected coevolving pairs. Coevolutionary z-scores were computed for all residue pairs for each domain–domain interface, and those pairs having a z-score larger than 8 were classified as coevolving (Materials and Methods). (Insets) The fraction of coevolving pairs closer than 8 Å (dark blue line) and 5 Å (light blue line) as a function of the threshold for the z-score. The dashed gray lines highlight the reference z-score threshold (z-score = 8) for detection of coevolution. We detected 62 coevolving pairs for interprotein interfaces (approximately three predictions per case on average) with an average precision of 0.81 for a contact distance of 8 Å (and 0.6 at 5 Å), and 1,140 pairs in the intraprotein case (approximately nine per case, on average) with a precision of 0.95 at 8 Å (and 0.83 at 5 Å). Precision and number of predictions for each of the 53 interprotein (C) and 245 intraprotein (D) domain–domain interfaces in prokaryotes with at least one detected coevolving pair. We obtained a precision of 0.86 at 8 Å and 0.74 at 5 Å for interprotein domain–domain interfaces (respectively 0.95 and 0.87 in the case of intraprotein interfaces).

Table S1.

Precision for contact predictions at eukaryotic interfaces

Set	Comprehensive		Representative
	Before filter	After filter	Before filter	After filter
Precision
Inter	0.81 ± 0.05	0.91 ± 0.04	0.74 ± 0.06	0.83 ± 0.05
Intra	0.95 ± 0.01	0.96 ± 0.01	0.90 ± 0.01	0.91 ± 0.01
Interface-averaged precision
Inter	0.77 ± 0.08	0.88 ± 0.06	0.69 ± 0.09	0.78 ± 0.08
Intra	0.90 ± 0.02	0.93 ± 0.02	0.87 ± 0.02	0.89 ± 0.02

Contact precision for inter- and intraprotein predictions and for both comprehensive and representative interfaces is given in the top half of the table. For each dataset, the precision has been computed using the formula ${\displaystyle \sum }_i^{N}T{P}_i/{\displaystyle \sum }_i^N(T{P}_i+F{P}_i),$ where TP_i and FP_i are, respectively, the number of true positive and false positives in the predicted contacts for the i-th interface. In the bottom half of the table interface-averaged contact precision is given, computed as the average precision over the set of interfaces in each dataset: $N^{-1}{\displaystyle \sum }_i^{N}T{P}_i/(T{P}_i+F{P}_i)$. SEs were obtained by bootstrap resampling (10,000 iterations with replacement).

Application to Mammalian Complexes.

The pyruvate dehydrogenase complex, responsible for the catalysis of pyruvate to acetyl-CoA and CO₂, is the complex in our dataset with the highest interface coupling in eukaryotes. Its E1 component forms a homodimer of heterodimers of its α and β subunits (40). The coevolving contacts detected by our protocol are distributed over the interface between the two subunits and are well conserved in the eukaryotic interface. Among the 13 coevolving pairs, 10 are in contact at the subunits interface of the branched-chain 2-oxo acid dehydrogenase remote homolog in the Thermus thermophilus structure (Fig. 4A) and are conserved in the human pyruvate dehydrogenase complex (Fig. 4B). Two out of three apparent false positives do actually correspond to contacts at the homodimer interface. These results show that coevolution has been key in the conservation of quaternary structure in the pyruvate dehydrogenase E1 component.

Fig. 4.

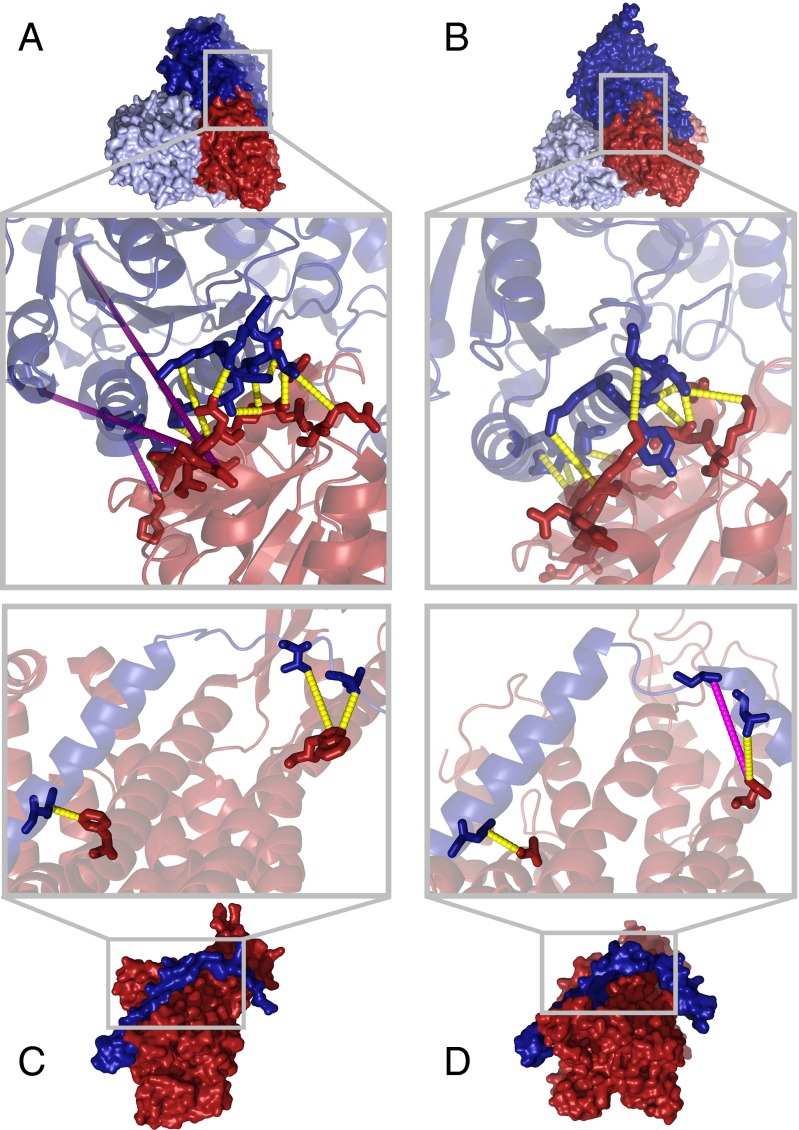
(A and B) E1 component of the branched-chain 2-oxo acid dehydrogenase in T. thermophilus [A, PDB ID code 1UMB (61)] and the human mitochondrial pyruvate dehydrogenase E1 component of the pyruvate dehydrogenase complex [B, PDB ID code 3EXI (40)]. In the zoomed inset coevolving pairs of residues are shown as sticks and connected by dashed lines (yellow if they are in contact, magenta otherwise). Ten contacts out of 13 coevolving pairs are detected at the T. thermophilus interface (A). Eleven out of these 13 pairs can be mapped to the human complex where they are all in contact (B). (C and D) Protein transportation channels across bacterial plasma membrane SecYE in T. thermophilus X-ray structure of SecY (in dark red) in complex with SecE (in dark blue) [C, PDB ID code 2ZJS (62)]. Eukaryotic endoplasmic reticulum Sec61 in C. lupus EM structure of Sec61 complex with its α subunit in dark red and γ subunit in dark blue [D, PDB ID code 4CG7 (63)]. The three coevolving pairs (drawn as sticks) are in contact in T. thermophilus and two of them are conserved in the C. lupus structure.

The translocon complex, one of the main mechanisms of transporting proteins across the membrane, is a good example of a conserved mode of interaction with very low sequence conservation. The α and γ subunits of the mammalian Sec61 are homologous to the bacterial proteins SecY and SecE, respectively. Despite the low sequence identity between these proteins in T. thermophilus and Canis lupus (18.8% SecY/Sec61α and 10.5% SecE/Sec61γ), and a strong structural divergence of the domains, two out of three coevolving contacts (Fig. 4C) have been conserved (Fig. 4D). In fact, seven out the nine residue pairs in the crystal structure for T. thermophilus with the highest coevolutionary z-scores are in contact and six of them are structurally conserved in C. lupus. The lower resolution (6.8 Å) of the available EM in C. lupus introduces some uncertainty on the definition of the interface. Still, our predictions support the overall arrangement of the interaction given in this experimental structure and highlight the potential use of our approach to refine atomic details of cryo-EM experiments.

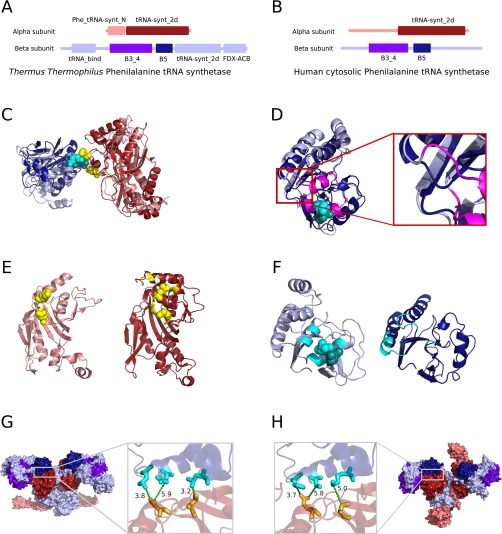
Among the 20 cases of interprotein interfaces with structural information in both eukaryotes and prokaryotes and with strong coevolutionary signals, we only detected one case where a strong coevolutionary signal does not go together with an, at least partially, conserved interface: the interaction between the α and β subunits of the phenylalanyl tRNA synthetase (PheRS). PheRS catalyzes the attachment of a phenylalanine amino acid to its cognate transfer RNA molecule. Despite important differences between the prokaryotic and the eukaryotic PheRS complexes (41), several homologous domains can be found in both the α subunit (core catalytic domain) and β subunit (B5 and B3/4 domains) between prokaryotes and eukaryotes (Fig. S8 A and B). The coevolutionary analysis of the interaction between the core catalytic domain and the B3/4 domain detects two coevolving pairs located at the T. thermophilus interface (Fig. S8C). These pairs are no longer aligned in the human B3/4 domain due to an insertion in the T. thermophilus PheRS compared with the human cytosolic complex as proved by a structural alignment (Fig. S8D) and therefore cannot be projected to the corresponding interface. Notably, this interacting region in human is deleted just at one of the two turns where the interaction takes place (Fig. S8D). Moreover, the α subunit also interacts with the B5 domain of the β subunit and the three coevolving contacts at the prokaryotic interface are completely preserved in the human PheRS (Fig. S8 G and H). This example illustrates that even after a drastic event, such as removal of a region at the interface in one of the interacting proteins, the remaining coevolving residues can keep pointing to the real interfaces.

Fig. S8.

(A and B) Pfam domains found in T. thermophilus (A) and human cytosolic (B) phenylalanine tRNA synthetase are shown as rectangles. Pfam domains found in both eukaryotes and prokaryotes are drawn in darker colors, core catalytic domain (Pfam: tRNA-synt_2d) in α subunit in dark red, B5 and B3/4 (Pfam: B3_4) domains in β subunit in purple and dark blue, respectively. (C) Superimposition of T. thermophilus (in light colors) PheRS structure [PDB ID code 1EIY (74)] and human PheRS (in dark colors) structure [PDB ID code 3L4G (41)] where the core catalytic domain (in reds) of both complexes have been structurally aligned. The B3/4 domains are shown in blues. Detected coevolving pairs are shown as cyan spheres in the B3/4 domains and yellow in core catalytic domain. (D) Structural alignment of the T. thermophilus (in light blue) and human (in dark blue) B3/4 domain. The insertion in the T. thermophilus B3/4 domain is drawn in magenta. (Inset) Zoomed-in view showing the inserted region in detail. (E) (Left) T. thermophilus core catalytic domain with interface residues in yellow and coevolving residues in yellow spheres. (Right) Human core catalytic domain with interface residues in yellow and projected coevolving residues in yellow spheres. Despite the changes at the interface of the B3/4 domain, projected coevolving residues at the human core catalytic domain are found at its interface. (F) (Left) T. thermophilus B3/4 domain with interface residues in cyan and coevolving residues in cyan spheres. (Right) Human core catalytic domain with interface residues in cyan. (G and H) The three coevolving pairs at the interface between the core catalytic domain and the B5 domain mapped to T. thermophilus (G) and human (H) structures are shown as sticks and connected by green dash lines together with the distance between the closest atoms in angstroms.

SI Text

Estimation of the Number of Human Protein–Protein Interactions with Structural Templates and/or Many Prokaryotic Sequences.

The potential practical impact of our results can be better explained by estimating the number of interactions in the twilight zone that could be modeled using prokaryotic coevolutionary information. We focused on human protein–protein interactions. The human interaction network represents a good reference, being one of the best characterized and most recently published interactomes. First, we retrieved a list of protein–protein interactions having enough eukaryota-to-prokaryota domain homologies. We determined how many of these interactions lack a reliable source of structural information (either from experiments or via homology modeling). Full details for the analysis are discussed below. We started from the network of human protein–protein interactions. For each pair of interacting proteins in this network (i) we looked for Pfam domains within them, (ii) we found the best (highest sequence identity) interaction template (PDB structure containing Pfam domains from both interactors, (iii) we determined the number of nonredundant prokaryotic sequences for Pfam domains in each interactor, and (iv) we estimated the subset of interactions with different interacting domains having enough prokaryotic sequence information but without reliable structural information.

We started from a comprehensive set of 214,806 known human protein–protein heterodimeric interactions, extracted from BIOGRID (64), involving 16,053 different human proteins. First, to be consistent with our protocol, we looked for Pfam domains in the principal isoforms of every interacting protein [APPRIS (65) version 2016_06.v17; Gencode24/Ensembl84 gene dataset]. A search with all of the Pfam HMM models (hmmsearch - -cut_ga) detected at least one significant human hit (covering a minimum of 80% of the Pfam profile) for 5,854 out of the 14,831 Pfam profiles. We also looked for significant hits (also covering at least 80% of the Pfam profile) of these HMM models in PDB (file pdb_seqres.txt, September 2016). We calculated the sequence identity between human and PDB hits for the same Pfam model based on their alignment to the corresponding profile (hmmalign - -trim - -allcol).

We classified the 214,806 heterodimeric human interactions in terms of the structural information available for them. For this, we considered all PDBs containing at least one Pfam domain from each interactor as putative templates of the interaction. For each combination of PDB and pair of Pfam domains, we selected the minimum of the two (one per domain) percentages of sequence identity (11) as reference. From these combinations we selected the best template (i.e., the one with the highest sequence identity). We classified the human interactions according to their sequence identities to its best template into four groups (Fig. S1): (i) 3,789 structurally solved interactions (≥98% identity), (ii) 13,253 interactions with reliable structural templates for homology modeling (<98% and ≥30% identity), (iii) 14,515 interactions with structural templates in the twilight zone (<30% identity), and (iv) 165,812 without template.

We next found which human protein–protein interactions have many homologous sequences in prokaryotes. To that aim, we searched the 5,854 Pfams in this human interactome against a nonredundant (below 80% identity using cd-hit) sequence database including the protein sequences from 15,271 prokaryotic genomes. For every interaction, we selected the pair of domains with the best template as explained above. When no template was available, we selected the pair of domains with more prokaryotic hits (again, we considered the minimum of the two possible numbers, one per domain). We detected 158,790 interactions where both interactors have at least one hit, 51,461 have 100, 36,213 have 500, and 22,958 have 1,000.

In summary, we retrieved 36,213 interactions (out of 214,806 total interactions) having at least 500 nonredundant prokaryotic homologs for both interactors. This suggests that up to ∼17% of the known human interactome can be currently addressable by our approach. Among these 36,213 interactions, we found 619 complexes that already have an experimentally solved 3D structure and 3,887 complexes with no solved structure but that are amenable to homology modeling (Fig. S1B). The remaining 31,707 cases are human interactions for which coevolutionary analysis of prokaryotic homologs could furnish novel structural information (Fig. S1A). This corresponds to ∼15% of the known human interactome and shows clearly that coevolution in prokaryotes has the potential of providing useful information for a significant number of structurally uncharacterized eukaryotic complexes. For 5,310 of these 31,707 cases we were able to detect possible templates in the twilight zone where our approach could also help to select good templates for homology modeling. Interestingly, for 23,433 of the 26,397 interactions without a template we could find good templates for the individual domains of both interactors. For these cases, our approach could be combined with protein docking methods to guide the selection of good models.

Dataset.

The 3did [version 06_2014 (37)] contains 8,651 pairs of Pfam domains with solved 3D structures, 4,556 of which are heterodimers. We run our protocol for these 4,556 heterodimers Pfam pairs. For 559 pairs of Pfam domains, our protocol produced joint alignments with more than 500 paired domain sequences (see SI Text, Domain–Domain Pairing Protocol). We classified each domain–domain interface as intra- or interprotein if the majority of paired sequences are codified within the same or different genes, respectively; 401 out of 559 domain pairs were classified as intraprotein and 158 as interprotein (Fig. 1B and Fig. S2C). Using the corresponding PDB sequence we classified each structure as eukaryotic or prokaryotic (as explained in the next paragraph).

Prokaryotic/Eukaryotic Structure Classification.

Using annotations from 3did, we retrieved the PDB identifiers, chains, and ranges of 37,126 domain–domain interfaces with known structure in PDB. Using their taxonomy identifiers extracted from SIFTS (66) annotations, we classified each PDB chain as prokaryotic or eukaryotic by traversing up the National Center for Biotechnology Information taxonomy (67) tree, all of the way up to the level of “Eukaryotes” or “Bacteria” or “Archaea.” Interfaces for which both interacting regions belong to the same chain (and are annotated in SIFTS) were classified correspondingly. Interfaces for which the two interacting regions belong to different PDB chains were classified when both chains were annotated in SIFTS in the same superkingdom (prokaryotes or eukaryotes; viruses were removed). Finally, we extracted the PDB sequences for the remaining unclassified structural interfaces and we searched them locally against a TrEMBL sequence database (68) using the blastp algorithm [version 2.2.18 (69)]. Sequences having a similar sequence in the TrEMBL sequence database (percentage of sequence identity > 80%) were annotated following the TrEMBL phylogeny annotations, and the interface was classified when the two interacting regions were annotated and belonged to the same superkingdom (prokaryotes or eukaryotes, not viruses). The remaining 387 unclassified pairs were discarded.

Domain–Domain Pairing Protocol.

Given a pair of Pfam domains (version 27.0), for each domain in the pair, our protocol searched for proteins containing a member of the corresponding Pfam family through hmmsearch (HMMER 3.0 package, hmmsearch - -noali - -domtblout - -cut_ga) across all of the coding regions of the 15,271 prokaryotic genomes [ensembl bacteria (56) release 23]. Our protocol implements two strategies to find interacting domains. The first strategy is by gene fusion and gene neighboring. The protocol checks whether there is (i) gene fusion—each hit found for the first domain has a hit of the second domain in the same protein; overlapping sequences are paired when the overlap is less than 10% of the smaller domain, up to a maximum of 20 residues, and the overlapping residues are removed in one of the two domains and (ii) gene neighboring—each hit found for the first domain has a hit of the second domain in another protein in the same contig but closer than 300 bp of nucleotides (using the annotation provided by ensembl bacteria). If the same Pfam domain appears more than once in a protein, these hits are discarded to avoid noise because it is not possible to ensure that all of them interact with its partner Pfam domain. The second strategy is by uniqueness across the genomes: The protocol checks whether both Pfam domains appear just once in a genome. Once the pairs are made, the sequences of each Pfam domain from each Pfam domain are separately aligned against the corresponding HMM Pfam profiles using the hmmalign command from HMMER (hmmalign - -trim - -allcol). The two output alignments are merged considering only matches states to the HMM profile. Several quality controls and filters are applied. (i) If the same sequence has more than one pairing, all of the pairs involving the sequence are removed to avoid any ambiguity. (ii) Any pair where one of the two sequences have more than 20% of gaps is discarded. (iii) Redundant paired sequences with greater than 80% sequence identity (considering both sequences as a whole) are filtered out using the cd-hit program [version 2 (70)] to reduce the phylogenetic bias.

Calculation of Coevolutionary Z-Scores.

For each domain–domain pair, coevolutionary z-scores were calculated from the parameters of a maximum-entropy model for protein sequences, based on pairwise interactions between positions in a joint sequence alignment. The maximum-likelihood solution of this problem can be directly tackled via Markov chain Monte Carlo-based inference (25). However, given the size of the benchmark dataset (559 cases) we resorted to a faster approximated solution based on multinomial logistic regression. Let $A_i$ be a discrete random variable representing the amino acids at position $i$ in a joint alignment, and taking values from an alphabet of 21 letters corresponding to the 20 natural amino acids plus the gap state. We performed multiclass logistic regression of each position $A_i$ on the remaining positions ${\mathit{A}}_{\backslash i}$ (23, 59), using a pairwise model of interaction between amino acids. In this model, the conditional probability of observing an amino acid $a_i$ at position $i$ given all of the others is given by $P\left(A_i=a_i|{\mathit{A}}_{\backslash i}={\mathit{a}}_{\backslash i}\right)\propto exp\left[h_i\left(a_i\right)+{\displaystyle \sum _j}{J}_{ij}\left(a_i,a_j\right)\right]$, where $a_i$ and $a_j$ are the amino acids at positions $i$ and $j$ of sequence $\mathit{a}$. For a given position $i$, the coupling parameters $\mathit{J}$ that regulate the interaction with the remaining positions in the alignment were inferred by maximization of a l₂-regularized version of the (log) conditional likelihood $L{L}_i\left(\mathit{h},\mathit{J}\right)$: ${\mathit{h}}^{\ast },{\mathit{J}}^{\ast }=argma{x}_{\mathit{h},\mathit{J}}\left\{L{L}_i\left(\mathit{h},\mathit{J}\right)-\lambda {\displaystyle \sum }_{\alpha }{h}_i^2\left(\alpha \right)-\lambda {\displaystyle \sum }_{j,\alpha ,\beta }{J}_{ij}^2\left(\alpha ,\beta \right)\right\}$, where $L{L}_i\left(\mathit{h},\mathit{J}\right)=N^{-1}{\displaystyle \sum }_{s}log\left[P\left(A_i=a_i^s|{\mathit{A}}_{\backslash i}={\mathit{a}}_{\backslash i}^s\right)\right]$, ${\mathit{a}}^s$ is the s-th sequence in the joint alignment, $N$ is the total number of sequences, and $\lambda =0.01$ (23). The procedure requires a numerical maximization for each position in the alignment. These calculations were conducted using an in-house Fortran code calling the MINPACK-2 (71) dvmlm routine, which implements a limited memory variable metric minimizer. Following a protocol proposed by Ekeberg et al. (23), the coupling values resulting from the regression of each position were double-centered, $J_{ij}^c\left(\alpha ,\beta \right)$ =$J_{ij}^{\ast }\left(\alpha ,\beta \right)-J_{ij}^{\ast }\left(\alpha ,:\right)-J_{ij}^{\ast }\left(:,\beta \right)+J_{ij}^{\ast }\left(:,:\right)$ where “:” denotes an average over the corresponding indices, and couplings from different positions were symmetrized, $J_{ij}^{sym}\left(\alpha ,\beta \right)=\left(J_{ij}^c\left(\alpha ,\beta \right)+J_{ji}^c\left(\beta ,\alpha \right)\right)/2$. A corrected Frobenius norm score (23, 30) was computed for each pair of residues. To reduce heterogeneity between cases, these values were standardized and used as coevolutionary z-scores: z-score$\left(i,j\right)$ = (score$\left(i,j\right)$ − median)/(1.4826 MAD), where median and MAD are the median and the mean absolute deviation of the scores of all of the pairs. An interdomain pair of residues was considered as coevolving when the corresponding coevolutionary z-score was higher than a threshold value of 8, that resulted in a good trade-off between number and precision of predictions. The precision of contact prediction was calculated as Prec = TP/(TP + FP) considering coevolving pairs of residues as positives.

Interface Definition.

For a given pair of Pfam families, we retrieved the biological unit for all of the structures of complexes in which two members of the families were in physical contact from the PDB. The PDB identifiers were retrieved from the 3did annotations. For structures with multiple biological units, the first one was selected. When a biological unit was not available, we analyzed the asymmetric unit. For NMR structures only the first model was considered. We extracted the PDB sequences and aligned them to their corresponding Pfam domains. We included in the analysis domain–domain interactions from the 3did annotations only when both domains were in the biological unit. When the biological unit contains more than one domain from the interacting Pfam families, we retrieved the shortest distance between all of the possible domain–domain combinations for each pair of residues. Disordered and unaligned residues were not included in the analysis.

Calculation of Eukaryote–Prokaryote Sequence Identities and Structural Conservations.

We classified each PDB structure as a eukaryotic or a prokaryotic structure. We defined one representative interface for these superkingdoms when at least one 3D structure is available (Materials and Methods). For those pairs of Pfams domains with structure in both prokaryotes and eukaryotes, we calculated the percentages of sequence identity between the eukaryotic and the prokaryotic representative complex. We calculated the sequence identities for the two Pfam domains using the alignments of the PDB sequences against the Pfam profiles obtained with hmmalign. Following ref. 11, we took the minimum of these two percentages of sequence identity as reference. The rationale behind this procedure is that the domain with the lower sequence identity tends to be a better estimator of the divergence in the interaction (11). For every pair of interacting Pfam domains with at least one eukaryotic and one prokaryotic structure, we defined its structural conservation as the percentage of contacts at the (comprehensive or representative) prokaryotic interface whose homologous positions are also in contact in the corresponding eukaryotic interface.

Domain–Domain Interactions with a High Coevolutionary Interface Coupling Correspond to Conserved 3D Interaction Topologies.

We partitioned the full list of domain–domain interfaces in two disjoint sets, one containing pairs of Pfam domains that always interact with a common, conserved topology in all of the available experimental structures (single-topology interfaces) and the other containing pairs interacting with variable topologies (multitopology interfaces). To classify a given pair of Pfam domains as single- or multitopology, we codified the topology of every experimentally available interface for that pair as a set of interdomain contacts. We defined a measure of similarity between the topologies of two interfaces $a$ and $b$ as $s_{ab}=n_{ab}/min\left\{n_a,n_b\right\}$, where $n_a$ is the number of contacts in the topology of interface $a$, $n_b$ is the number of contacts in topology of interface $b$ and $n_{ab}$ is the number of contacts shared by the two topologies. Two interfaces $a$ and $b$ are defined to have a similar topology when $s_{ab}>0.1$ (i.e., when they have at least 10% of the contacts of the smallest domain in common). The final results do not change qualitatively for thresholds in the range 0–0.3. Interfaces with fewer than 10 contacts were excluded from the analysis. Using this definition, for each interface $a$ we counted the number of interfaces with a similar topology contained in the structural set for this pair of domains (including interface $a$), $R_a$. The $\left\{R_a\right\}$ values were used to down-weight redundant interfaces (having a topology similar to many others interfaces) in the calculation of an effective number of topologies, $n_{eff}={\displaystyle \sum }_{a}1/R_a$. Finally, Pfam domain–domain pairs having $n_{eff}<1.5$ were classified as single-topology, and the others as multitopology. The 49 pairs with the largest interface coupling (see the main text for the definition of interface coupling) correspond to single-topology cases. The statistical significance of this result was evaluated by shuffling the classification in single- and multitopology and computing the number of single-topology cases having an interface coupling larger than the maximum value observed in multitopology pairs. The procedure was repeated 10⁶ times. The observed value of 49 is statistically significant with P $\sim$ 0.001.

Statistical Analysis of Preferential Structural Conservation of Coevolving Contacts.

The preferential structural conservation of coevolving contacts was evaluated by applying Fisher’s exact test. The contingency table is based on two conditions: structurally conserved contact/nonconserved contact and coevolving contact/noncoevolving contact. We compared the proportion of expected conserved contacts with the proportion of conserved contacts in the presence of strong coevolutionary signals. Given a contact threshold, a contact in the prokaryotic structure comprehensive (or representative) interfaces is structurally conserved if the corresponding homologous sites are also in contact in the eukaryotic comprehensive (or representative) interface; otherwise they were considered not conserved. Coevolving pairs of residues were defined as those with a coevolutionary signal above a given coevolutionary threshold; otherwise, they were considered as noncoevolving. The results of the test were P ∼ 10⁻¹² for interprotein cases (48 conserved contacts out of 52) and P ∼ 10⁻¹⁸⁸ for intraprotein cases (1,039 out of 1,070). A similar conservation was observed when the 10 first predictions (with annotated distances in both prokaryotes and eukaryotes) for each case were considered (interprotein: 118 out of 135, P ∼ 10⁻²⁴; intraprotein: 989 out of 984, P ∼ 10⁻¹³⁰). When considering only cases with lower than 30% sequence identity, interprotein P ∼ 10⁻⁷ (23 out of 24) and intraprotein P ∼ 10⁻¹⁰⁷ (583 out of 607).

Comparison of Conservation in Sequence and Coevolutionary Signals.

In general, coevolving residues cannot be completely conserved, but because they reflect evolutionary constraints their sequence conservation could be enough to predict some structural conservation. To address this point, we first examined the distribution of the entropies of sequence positions (see Fig. S3E, logarithms to base 21) for two sets of residues: interface residues (residues involved in a domain–domain contact, red histogram) and coevolving residues (residues involved in a coevolving pair, blue histogram). The peak at low entropy values (centered at ∼0.1) corresponds to highly conserved positions in the alignment(s). Coherently with the fact that some degree of variation is needed to detect coevolution, the peak associated to highly conserved positions is clearly absent in the distribution of entropies for the coevolving residues. The set of coevolving residues is enriched in positions of intermediate variability (entropies in the range 0.4–0.7). The structurally conserved contacts detected by coevolution could be statistically associated to this intermediate regime of conservation in sequence. To rule out this possibility, we created a corrected set of contacts by selecting pairs of residues with a probability that depends only on the entropy of the corresponding positions. This probability has been chosen such that the corrected set has the same entropy distribution of the coevolving set. More specifically, we computed the joint probability $P\left(H_a,H_b\right)$ of observing, for a pair of residues in contact, two entropy values $H_a$ and $H_b$ from the corresponding positions in the sequence alignment. We also computed the joint distribution $P_C\left(H_a,H_b\right)$ restricted to contacts involving coevolving pairs. The entropy of a position in a sequence alignment has been computed using the standard formula $H\left[\pi \right]=-{\displaystyle {\sum }_a\pi \left(a\right){\log }_{21}\pi \left(a\right)}$, where $\pi$ is the estimated distribution of amino acids (the 20 natural amino acids plus the gap state) for the position. $\pi$ was estimated adding 21 pseudocounts to the statistics from the alignment, $\pi \left(a\right)=\left(n_a+1\right)/\left(N+21\right)$, where $n_a$ is the empirical frequency of amino acid $a$ and $N$ is the total number of sequences in the alignment. The joint probabilities were computed by binning the range of possible entropy values (to base 21) using a bin size of 0.1. Finally, for each pair of residues in contact $\left\{x,y\right\}$, we computed a weight $w\left(x,y\right)=P_C\left(H\left[{\pi }_x\right],H\left[{\pi }_y\right]\right)/P\left(H\left[{\pi }_x\right],H\left[{\pi }_y\right]\right)$, where $H\left[{\pi }_x\right]$ and $H\left[{\pi }_y\right]$ are the entropy values corresponding to the positions $x$ and $y$ in the alignment. These weights define a corrected ensemble of contacts that by construction has the same joint distribution of entropies than the restricted set of contacts involving only coevolving residues, $P_C\left(H_a,H_b\right)$. Averages over contacts in this corrected ensemble can be computed as weighted averages: $\langle A\rangle ={\displaystyle {\sum }_{\left\{\mathit{x},\mathit{y}\right\}}A\left(x,y\right)w\left(x,y\right)}/{\displaystyle {\sum }_{\left\{\mathit{x},\mathit{y}\right\}}w\left(x,y\right)}$. If sequence conservation was enough to explain structural conservation of coevolving residues (i.e., if the statistical relation between coevolution and conserved contacts could be explained by conservation in sequence), conserved contacts in the corrected ensemble should be as frequent as in the coevolving set. As shown in Fig. S3F, however, the probability of conserved contacts in the corrected ensemble is almost identical to the naive background computed over all pairs (see also Fig. 2B). In fact, contact conservation in coevolving pairs remains highly significant (P < 10⁻¹⁰, one-tailed Fisher exact test for both interprotein and intraprotein cases) when considering this corrected reference distribution, demonstrating that sequence conservation does not explain the precision of our protocol based on coevolution.

Structural Conservation of Coevolving Contacts at Long-Sequence Evolutionary Distances.

We explored an alternative definition of the twilight zone based on evolutionary distances. To perform comparable evolutionary analyses for all of the cases in our benchmark, we selected a set of 89 reference proteomes including both eukaryotic and prokaryotic species (listed below). Our set of reference species combines the species used for two recent whole-proteome phylogenetic analyses (www.phylomedb.org/phylome_514 and www.phylomedb.org/phylome_28) in phylomeDB (72). We also included four additional species (T. thermophilus HB8, Staphylococcus aureus, Sus scrofa, and Oryctolagus cuniculus) for which SIFTS associated more than 500 PDB chains in our benchmark. We searched in these proteomes (hmmsearch - -cut_ga) for the 274 Pfam interacting domains in the 195 cases with structures for homologs in prokaryotes and eukaryotes (discussed above). We aligned the significant hits in these proteomes and the sequences from the representatives PDBs in our benchmark to the corresponding Pfam profiles discarding nonhomologous residues (hmmalign - -trim - -allcol). Maximum-likelihood trees were inferred from these alignments using IQ-TREE (73) (options -m TESTNEWONLY -b 100 -nt 2; version 1.4.4). Seven cases were discarded because one of the interactors had not enough sequences on the reference proteomes (fewer than four sequences). Evolutionary distances were calculated as the branch distance in the tree between the prokaryotic and eukaryotic structural representative sequences (tree leaves). For each case, in analogy to sequence identities (discussed above), we selected the largest evolutionary distance of the two interacting domains. A direct comparison of sequence identities and evolutionary distances obtained with this protocol shows that they are highly correlated (Spearman’s correlation approximately −0.8; see Fig. S5E). We analyzed the conservation of coevolving residues in highly divergent cases using evolutionary distance as a measure of divergence. We first estimated the value of evolutionary distance equivalent to 30% sequence identity as the median evolutionary distance (2.88) of the cases with a sequence identity between 27% and 33%. Any case with an evolutionary distance higher than 2.88 is thus considered as belonging to the twilight zone according to its evolutionary distance. This criterion corresponds to a more stringent definition of the twilight zone including 109 instead of the 125 cases with less than 30% sequence identity. The precisions for the predicted cases in both definitions of the twilight zone are very similar (0.86 for 80 predicted out of 109 cases by evolutionary distance compared with 0.87 for 83 predicted out of the 125 cases by sequence identity). In fact, 95.6% (549 out of 574) of the coevolving contacts in prokaryota are conserved in eukaryota; this proportion is 93.3% (14 out of 15) for interprotein and 95.7% (535 out of 559) for intraprotein cases. These figures are very similar to those obtained for the twilight zone based on sequence identities (discussed in the main text), showing that our observations about the structural conservation of coevolving residues in interfaces are robust to the measure of sequence divergence used to define the twilight zone.

The species names of the 89 reference proteomes used in this analysis are as follows:

• Anopheles gambiae, Aquifex aeolicus VF5, Arabidopsis lyrata, Arabidopsis thaliana, Aspergillus fumigatus A1163, Bacillus subtilis, Bacteroides thetaiotaomicron VPI-5482, Bos taurus, Brachypodium distachyon, Bradyrhizobium japonicum, Branchiostoma floridae, Caenorhabditis elegans, Candida albicans, Canis familiaris, Chlamydia trachomatis A/HAR-13, Chlamydomonas reinhardtii, Chloroflexus aurantiacus J-10-fl, Ciona intestinalis, Cryptococcus neoformans var. neoformans JEC21, Cucumis sativus, Danio rerio, Deinococcus radiodurans R1, Dictyoglomus turgidum DSM 6724, Dictyostelium discoideum, Drosophila melanogaster, Escherichia coli K-12, Fusobacterium nucleatum subsp. nucleatum ATCC 25586, Gallus gallus, Geobacter sulfurreducens PCA, Giardia lamblia ATCC 50803, Gloeobacter violaceus PCC 7421, Glycine max, Halobacterium sp. NRC-1, Homo sapiens, Ixodes scapularis, Korarchaeum cryptofilum (strain OPF8), Leishmania major, Leptospira interrogans serovar Lai str. 56601, Macaca mulatta, Medicago truncatula, Methanocaldococcus jannaschii DSM 2661, Methanosarcina acetivorans C2A, Micromonas pusilla CCMP1545, Mimulus guttatus, Monodelphis domestica, Monosiga brevicollis, Mus musculus, Mycobacterium tuberculosis, Nematostella vectensis, Neurospora crassa, Ornithorhynchus anatinus, Oryctolagus cuniculus, Oryza sativa subsp. indica, Oryza sativa subsp. japonica, Ostreococcus lucimarinus (strain CCE9901), Ostreococcus tauri, Pan troglodytes, Phaeosphaeria nodorum SN15, Physcomitrella patens subsp. patens, Physcomitrella patens subsp. patens, Plasmodium falciparum 3D7, Populus trichocarpa, Pseudomonas aeruginosa PAO1, Rattus norvegicus, Rhodopirellula baltica SH 1, Ricinus communis, Saccharomyces cerevisiae, Schistosoma mansoni, Schizosaccharomyces pombe (strain 972/ATCC 24843), Sclerotinia sclerotiorum 1980 UF-70, Selaginella moellendorffii, Sorghum bicolor, Staphylococcus aureus, Streptomyces coelicolor A3 (2), Sulfolobus solfataricus P2, Sus scrofa, Synechocystis sp. PCC 6803 substr. Kazusa, Takifugu rubripes, Thalassiosira pseudonana, Thermococcus kodakarensis KOD1, Thermodesulfovibrio yellowstonii DSM 11347, Thermotoga maritima MSB8, Thermus thermophilus HB8, Trichomonas vaginalis, Ustilago maydis, Vitis vinifera, Xenopus tropicalis, Yarrowia lipolytica, and Zea mays.

Alignment Quality Measurement.

To estimate how the alignment quality was affecting to our interdomain couplings at the interface, we calculated the average minimum expected alignment quality of the eukaryotic sequences. We used the PDB sequences of the eukaryotic representative complexes (Materials and Methods) and considered the homologous sites at the eukaryotic sequence of the residues at the prokaryotic comprehensive interface. We recovered the expected alignment quality per residue obtained by HMMER and considered gaps as positions with 0 expected quality. We averaged the expected alignment quality per residue for each one of the two domains, and selected the minimum of these two averages. To avoid the requirement of a structurally solved interface at prokaryotes, we calculated an equivalent score based on the coevolving residues. In this case, we are targeting cases where a low quality alignment is associated to those residues detected as interdependent. If the expected alignment quality measurement is equal to or less than 0.8, the corresponding case is identified as poorly aligned (Fig. S7).

Data Availability.

All of the data discussed in this work is available at the website cointerfaces.bioinfo.cnio.es.

Discussion

In this work we introduce and validate an important property of coevolving contacts at protein interfaces: their propensity to be preferentially conserved at large evolutionary distances. This behavior is confirmed by the analysis of coevolving residues between domains in 15,271 prokaryotic genomes and their homologous sites in 3D structures of eukaryotic complexes. This previously unrecognized aspect of the evolution of protein interfaces highlights the important role of coevolving residues in maintaining quaternary structure and protein–protein interactions. As a first and important consequence of this property, we show that contacts at eukaryotic interfaces can be predicted with high accuracy using solely prokaryotic sequence data, both for protein–protein and for domain–domain interfaces. We tested these conclusions by analyzing a large dataset of prokaryotic/eukaryotic interfaces with a domain-centered protocol. We were able to predict contacts in interprotein eukaryotic complexes with a mean precision >0.8 (Fig. 3 and Table S1). This result is particularly relevant taking into account that this level of accuracy was attained for predictions of contacts in highly divergent complexes (sequence identities lower than 30%), where standard homology modeling is hardly useful. We have also shown that the few errors in these prokaryote–eukaryote projections are generally associated to cases with low structural conservation that can be detected a priori by checking the alignment quality. Moreover, we extended this analysis to domain–domain contact predictions, showing that intraprotein interfaces exhibit even stronger coevolutionary signals, leading to an increased precision in contact prediction. The analysis protocol we propose relies on sequence data only. As a consequence, our strategy can provide useful information on a protein interface both in remote homology-based complex reconstruction and when no structural template is available, and it is inherently complementary to current methods based on the analysis of structural similarity (42) or sequence similarity (6, 7, 10, 43) to a set of available templates.

The main obstacle to structural modeling of eukaryotic protein complexes by means of coevolution-based approaches is the need for a large number of homologous interactions to permit statistical analysis. Eukaryotic complexes present a paradoxical scenario: Large families of eukaryotic proteins are the result of duplication-based expansions, but these duplications make uncertain which paralogues of one family interact with which ones of the other. In the future, improvements aimed to disentangle the network of paralogous interactions will be fundamental to deal with eukaryotic interactions (44–47). Our approach, based on preferential conservation, tackles this problem for proteins with prokaryotic homologs by looking at very divergent, well-populated, and easy-to-couple pairs of interacting prokaryotic proteins. This strategy cannot be applied in some specific contexts; for example, our approach cannot cope with recently evolved interactions, or with disordered—and difficult-to-align—interfacial regions. However, we found enough prokaryotic homologs to perform these analyses for 31,707 experimentally known human interactions without reliable structural templates (an estimated 15% of the human interactome; SI Text), suggesting that large-scale prediction of contacts at eukaryotic interfaces is actually possible. The resulting projected contact predictions represent a source of structural information that can be easily incorporated in integrative structural computational methods (48–52) or used to improve the scope of the successful methods that already incorporate coevolutionary information from closer homologs (24, 29, 30, 53–55). At a more general level, these results indicate that coevolving contacts have played a fundamental role in the evolution of interacting surfaces as structurally conserved anchor points.

Materials and Methods

Dataset and Joint Alignments.

We extracted a list of 4,556 heterodimeric pairs of interacting Pfam domains with solved 3D structures [3did database (37)]. For each pair of Pfam domains, our protocol searched for proteins containing members of at least one of these two Pfam domain families in 15,271 prokaryotic genomes (56) using HMMER software (version 3.0) (57, 58). Two domains were paired if they were in the same protein, adjacent proteins, or when both had no other paralogous in the corresponding genome. From this set of pairs, a joint alignment was built by aligning each domain to its corresponding Pfam profile. We next applied a stringent set of quality controls (SI Text) including alignment coverage (>80%) and redundancy (<80%). Insertions were removed by considering only residues that were assigned to match states of the HMM model. We retained 559 domain–domain interactions with a large number of nonredundant sequences (>500) for further analyses. Each pair of Pfam domains was classified as intra- or interprotein if the majority of paired sequences are codified within the same or different genes, respectively (Fig. S2C).

Calculation of Coevolutionary Z-Scores.

We retrieved the coevolutionary z-scores by performing a (multinomial) logistic regression of each position in the joint alignment on the remaining positions, a standard network inference strategy (59) that has already been adopted for the analysis of monomeric protein sequences (23) in combination with l₂ regularization. For each residue–residue pair we computed the corrected Frobenius norm score (23), a measure of statistical coupling between residues, from the (symmetrized) estimates of the coupling parameters. Finally, these values were standardized to reduce heterogeneity between cases and used as coevolutionary z-scores. An interdomain pair of residues was considered as coevolving when its coevolutionary z-score was higher than a threshold value of 8 (see SI Text for details).

Interface Definition and Contact Prediction Evaluation.

For a given pair of Pfam families, we retrieved, from the Protein Data Bank (PDB) (60), the biological unit for all of the structures of complexes in which two members of the families are in physical contact. The PDB identifiers were retrieved from the 3did annotations. For structures with multiple biological units, we selected the one labeled as first. We extracted the PDB sequences and aligned them to their corresponding Pfam domains. We classified each PDB structure as eukaryotic or prokaryotic (SI Text). We defined a comprehensive and a representative interface in one or both superkingdoms depending on the availability of at least one 3D structure in prokaryotes and/or eukaryotes. To that aim, for each pair of Pfam domains (i) we recovered the interdomain contacts in all PDB containing those Pfam domains. We used a distance of 8 Å between any heavy atom as the distance threshold for contacts (29, 30). Other contact definitions were used and are shown when appropriate. (ii) We mapped all PDB positions to their corresponding positions in the Pfam HMM profiles. (iii) We selected the most reliably aligned PDB (according to the alignment bitscores; SI Text) as the representative complex in prokaryotes and eukaryotes. (iv) Using the alignments of PDB sequences against both Pfam domains, we retrieved the set of PDBs with a 98% or higher percentage of sequence identity with respect to the representative complex. The representative interface is composed by the collection of contacts of the PDBs in this latter set, whereas the comprehensive interface is composed by all of the contacts found in the PDBs containing the Pfam domains. Both interfaces were separately computed for eukaryotes and prokaryotes. Only pairs of interdomain residues that were both aligned and having geometric coordinates in at least one PDB file were used to compute the precision of contact predictions.