Rules to fly by: pigeons navigating horizontal obstacles limit steering by selecting gaps most aligned to their flight direction

Abstract

Flying animals must successfully contend with obstacles in their natural environments. Inspired by the robust manoeuvring abilities of flying animals, unmanned aerial systems are being developed and tested to improve flight control through cluttered environments. We previously examined steering strategies that pigeons adopt to fly through an array of vertical obstacles (VOs). Modelling VO flight guidance revealed that pigeons steer towards larger visual gaps when making fast steering decisions. In the present experiments, we recorded three-dimensional flight kinematics of pigeons as they flew through randomized arrays of horizontal obstacles (HOs). We found that pigeons still decelerated upon approach but flew faster through a denser array of HOs compared with the VO array previously tested. Pigeons exhibited limited steering and chose gaps between obstacles most aligned to their immediate flight direction, in contrast to VO navigation that favoured widest gap steering. In addition, pigeons navigated past the HOs with more variable and decreased wing stroke span and adjusted their wing stroke plane to reduce contact with the obstacles. Variability in wing extension, stroke plane and wing stroke path was greater during HO flight. Pigeons also exhibited pronounced head movements when negotiating HOs, which potentially serve a visual function. These head-bobbing-like movements were most pronounced in the horizontal (flight direction) and vertical directions, consistent with engaging motion vision mechanisms for obstacle detection. These results show that pigeons exhibit a keen kinesthetic sense of their body and wings in relation to obstacles. Together with aerodynamic flapping flight mechanics that favours vertical manoeuvring, pigeons are able to navigate HOs using simple rules, with remarkable success.

1. Introduction

Moment-to-moment navigation through a complex obstacle-laden ecosystem is necessary for the evolutionary success and survival of flying animals. Flight navigation through cluttered environments requires exceptional aerodynamic manoeuvring performance coordinated by rapid processing of sensory cues. The manner in which flying animals manoeuvre to avoid obstacles and select flight paths has become a growing focus of investigation. Studies of animal flight navigation also hold promise for inspiring more robust algorithms for short-range navigation of unmanned aerial systems (UAS) [1,2].

Birds and insects rely heavily on visual cues for short-range navigation to avoid obstacles, pursue prey [3–5] and select flight paths [6–13], whereas many bats and some specialized species of birds [14,15] rely on echolocation when foraging and during transit flights [16–19]. When flying through narrow openings, birds demonstrate a strong kinesthetic sense of body position and movement with respect to nearby obstacles, reducing their risk of wing and/or body damage associated with obstacle contacts [20–22].

Obstacle negotiation is also arguably a central component of successfully deploying autonomous mobile robots in unstructured real-world environments. The main challenges in obstacle negotiation are to identify relevant obstacles, determine the manoeuvres needed to avoid them and to execute the manoeuvres with appropriate dynamics. Obstacle avoidance can be achieved via path planning and/or reactive control [23]. Path planning requires some level of spatial map information [24]. However, for many robotic applications, an accurate map of the environment is not available and can be computationally expensive to obtain. Instead, the use of relatively simple sensory heuristics for guidance provides an alternative approach and has been explored to model visual guidance by animals, ranging from insects to humans [25–29]. Such a heuristics approach has been successfully used to guide autonomous robots. Good examples are UAS obstacle avoidance and autonomous landing, using optic flow [30–32]. Understanding the behavioural strategies, used by animals for guiding movement in cluttered environments, has key relevance to robotic applications.

Behavioural strategies, however, are difficult to extract, because an animal typically integrates multiple sensory cues and chooses from a multitude of possible actions. Visually guided behaviours constrain the role of sensory modalities, which can be further simplified, using an artificial visual environment [11,13,33]. In past work [34], we developed a simple obstacle negotiation behavioural paradigm and modelling procedure to evaluate possible behavioural strategies used by pigeons (Columba livia) to navigate through an artificial forest. By recording the flight trajectories of the pigeons in the horizontal (XY) plane and combining their trajectories with obstacle positions, we were able to reconstruct the visual cues that pigeons might use to navigate past obstacles. Rather than using obstacle avoidance strategies [29,35] or time-to-collision (τ) [36,37] as steering cues, we developed a gap-aiming guidance model based on proportional-derivative (PD) control with a fixed delay. We extensively searched for the gains and visuomotor delays that best described the observed manoeuvring flight trajectories. We used our model to test whether pigeons selected the widest gap or the gap most in line with their flight direction to navigate past vertical obstacles (VOs). We found VO negotiation was best described by proportional steering control driven by the error between their flight direction and the desired opening, with pigeons biasing their steering towards larger gaps, rather than those most in line with their flight bearing or their destination direction. A widest gap-aiming model was able to predict up to 80% of the observed flight paths, given only the initial conditions.

Flying animals must navigate past horizontal as well as VOs when flying through natural environments. An obstacle's orientation relative to the wing stroke plane imposes fundamental constraints on obstacle avoidance biomechanics and aerodynamics. While VOs require pigeons and other flying animals [21,22] to pause at the end of a stroke reversal or narrow their wingspan at mid-stroke, horizontal obstacles (HOs) likely allow birds to keep their wings extended for brief glides to manoeuvre past obstacles. Whereas VOs challenge a bird to generate lateral forces, HOs require changes in vertical force, which therefore require different aerodynamic mechanisms. Here, we examine the flight trajectories and strategies that pigeons adopt to negotiate HOs and propose three hypotheses according to biomechanical and aerodynamic constraints. First, the control authority of birds is likely greatest in the vertical plane, as the majority of aerodynamic lift production is to support the animal's weight against gravity. We therefore expect pigeons to navigate HOs at higher average speeds, but assist braking and conserve energy by converting kinetic energy (KE) into potential energy (PE), resulting in an upward bias of their flight trajectories. Second, because the bird's body–wing profile is oriented more parallel to the HOs, the acceptable gap size for navigation between obstacles may be much smaller. We therefore expect that the widest gap-aiming model may not best describe HO navigation in the vertical plane, as it did for VO navigation in the horizontal plane [34]. Finally, pigeons must make adjustments in wing stroke amplitude and stroke plane angle to avoid contact with the obstacles, while also controlling body pitch to adjust flight trajectories through HOs. We test these hypotheses by analysing pigeon kinematics during HO flight.

2. Material and methods

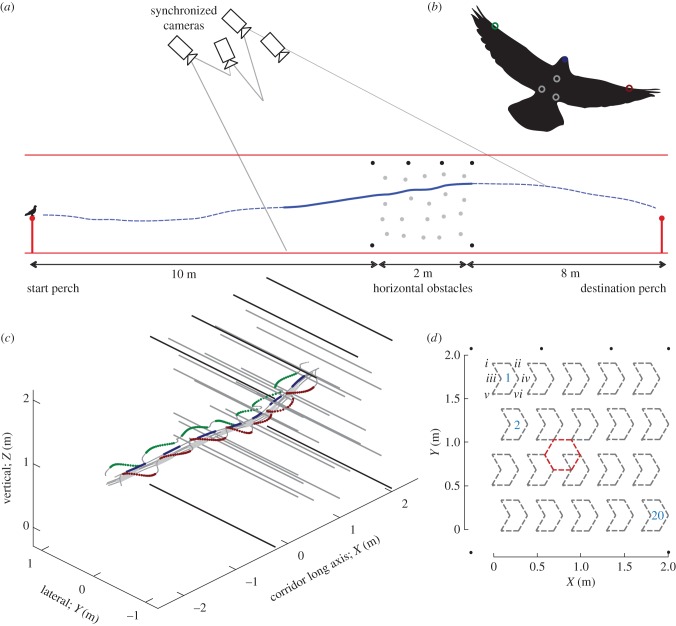
Four wild-caught adult rock doves, C. livia, (pigeons; 353 ± 37 g body mass) used in the experiments were housed, trained and studied at the Concord Field Station (Bedford, MA) in accordance with protocols approved by Harvard University's Institutional Animal Care and Use Committee (animal experimentation protocol no.: 98-04). Over the course of two weeks, seven pigeons were trained to fly between two 1 m high perches and vocally discouraged from landing on the floor. The interperch distance was gradually increased until the perches were positioned permanently on either end of a 3 m wide by 3 m high by 20 m long corridor. The four pigeons that flew most consistently (as subjectively assessed by the trainer) were selected as study subjects for flight navigation. Following training, 20 HOs (HO, 1.25 cm× 3 m, figure 1a) were semi-randomly positioned across a hexagonal lattice with edges of 0.2 m. For each trial, an obstacle was semi-randomly allocated to one of six locations for each of 20 grid locations on a 2×2 m area (figure 1d). The HO forest started 10 m from the obstacle flight take-off perch and ended 8 m before the landing perch (similar corridor location as for our prior study of VO flight [34]). The resulting HO distributions averaged 4.8 obstacles m⁻², significantly denser than the VO forest in our previous study, which averaged 1.7 obstacles m⁻². However, the VOs had a diameter of 3.8 cm, substantially exceeding the 1.25 cm diameter of the HOs used here. We used Bungee™ cords drawn tight between eye-bolt anchors installed in the lateral walls of the obstacle field as HOs (rather than the plastic poles used for the VO navigation study), to ensure that the pigeons would not land on an obstacle but would fly through the obstacle field to land on the far perch. Four permanent HOs were set above and two permanent obstacles were set near the ground (black dots, figure 1a) to ensure that the pigeons navigated through the HO forest. For simplicity, we refer to flights without the 20 semi-randomly distributed obstacles as non-obstacle flights (NO flights), even though the six permanent obstacles were present for all flights. The walls of the corridor were uniformly covered with white polyethylene sheets.

Figure 1.

Flight corridor with horizontal obstacles (HOs). (a) Pigeons were trained to fly down a 3 m wide × 3 m high × 20 m long corridor between two 1 m high perches (dashed blue line; takeoff—left; landing—right). The corridor ceiling was covered by plastic mesh netting to enable four high-speed video cameras to capture the pigeon's flight paths from above. Flights were recorded (solid blue trace) from 2 m prior to, until passage through, a forest of HOs (black and grey dots). (b) Infrared, 2.4 mm LEDs mounted on the bird's head, body and wings (coloured circles on black silhouette) were tracked in the camera views and used to reconstruct three-dimensional flight positions. The head centre (blue dot) was approximated by a weighted average of two head LEDs (not shown). (c) Marker positions for an example flight through the HOs (thick black and grey lines). Upstroke phases are depicted in small, grey symbols, whereas downstroke phases are in bold for the left (green) and right (purple) wings, along with the body (grey) and head (blue). (d). Four fixed HOs (black) define the upper height of the field, and two fixed obstacles (black) were placed near the ground. Within an evenly distributed grid (grey dashes), 20 HOs (grey dots and lines in (a) and (c), respectively) were semi-randomly allocated to one of six locations (i–vi) for every trial. The resulting obstacle distributions across a hexagonal lattice with edges of 0.2 m (red dashes) yielded an average obstacle density of 4.8 obstacles m⁻².

Four synchronized high-speed video cameras (two Integrated Design Tools, Inc. model N5S1 recording 2336 × 1728 pixel images and two Photron model PCI recording 1024 × 1024 pixel images) recorded the pigeons' flight trajectories at 250 Hz. The calibrated volume of the four cameras included the HO field, as well as an approximately 2 m approach to the obstacles (figure 1a). Infrared LEDs were used as active markers to facilitate tracking of key landmarks on the birds (figure 1b; Vishay Intertechnology, Inc., Malvern, PA). The LEDs were powered by a battery pack secured to the dorsal side of the torso, near the centre of mass of the bird. Two LEDs attached to either end of a 5.5 cm piece of balsawood were secured to the bird's head with thermoplastic adhesive and elastic tape. A weighted average of these two LEDs approximated the centre of the head. Three LEDs mounted via elastic tape to the bird's torso provided three-dimensional measurements of body position and orientation. The feathers on the dorsal side of the head and the torso were carefully trimmed to reduce relative motion of the LEDs. LEDs mounted halfway along the shaft of the ninth primary of the left and right wings were used to calculate kinematic variables relevant to flight manoeuvres (table 1 and figure 5c,d). To prevent the wires from interfering with wing motion, we secured the wires with small amounts of thermoplastic adhesive to the ventral side of the elbow and wrist joints, while guiding the wires along the ventral side of brachium and antebrachium of each wing. The weight of all components added to each bird totalled 9.7 ± 0.8% of their body mass.

Table 1.

Local wing kinematics, normalized to NO flight downstroke values. Mean ± s.d. of individual wing kinematics. Significant differences between NO and HO flights are in italics.

	stroke amplitude (%)	stroke duration (%)	wing speed (%)	wing extension (%)	stroke plane angle (%)
downstroke
NO flights	100	100	100	100	100
HO flights	103.3 ± 13.0	92.4 ± 10.3	113.5 ± 24.5	93.3 ± 3.2	77.9 ± 6.6
upstroke
NO flights	98.7 ± 4.1	98.8 ± 6.0	110.1 ± 3.8	78.7 ± 6.7	91.3 ± 2.4
HO flights	100.4 ± 14.7	82.7 ± 10.5	123.2 ± 28.0	60.0 ± 5.3	73.9 ± 6.9

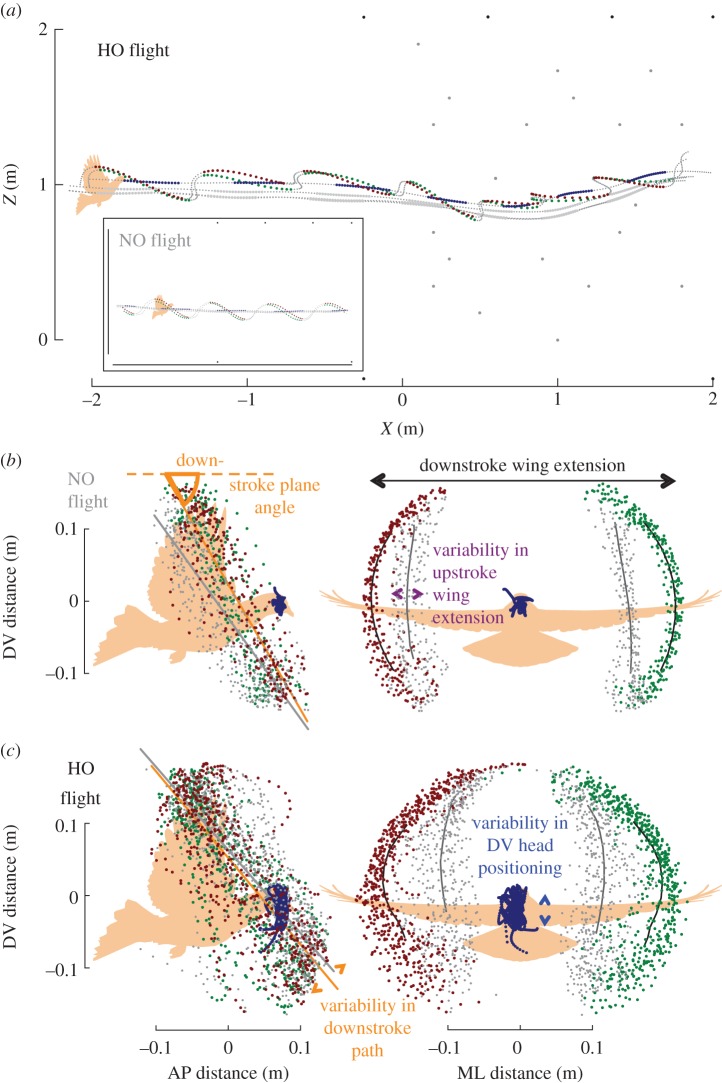
Figure 5.

Horizontal obstacle (HO) manoeuvring is associated with changes in wing stroke trajectories and wing extension, as well as increased head movements. (a) Lateral view of a representative HO flight (same trial as figure 1d) as the pigeon approaches and then flies through the HO forest (20 grey circles semi-randomly distributed at right). Wing stroke patterns (left, green; right, red) are stereotypic during downstroke (larger, coloured symbols) and upstroke (smaller, grey symbols) as the pigeon approaches, but exhibit variable paths to navigate between obstacles and to avoid obstacle contacts. Positions of the head during downstroke (large blue symbols) and upstroke (small grey symbols) are shown relative to the three body markers (grey points) and are, not surprisingly, less variable in their trajectory than the motions of the bird's wings. Wing and body motions during NO flight (lower left inset) are highly regular in pattern, similar to those observed during the approach section to the obstacle field in the HO flight. (b,c) Lateral and frontal views of the left (green) and right (red) wing trajectories relative to the body, together with head positions (blue), follow more regular movement patterns during NO flight (b) compared with flight in the HO forest (c). Regressions of wing paths during downstroke (orange) and upstroke (grey) document wing stroke plane angles relative to the anteroposterior body axis (orange arc, left panel for the downstroke plane angle). The stroke plane angles for both the downstroke and upstroke are lower in the forest, compared with NO flights, for the represented individual and across individuals (table 1). The reduced stroke plane angles are caused by more anteriorly swept wings during downstroke. The pigeons also reduce their wingspan in the obstacle forest, both during downstroke and upstroke (shown for downstroke in frontal view). Furthermore, HO manoeuvres are associated with more variable wing extension ((b), right panel) and stroke paths ((c), left panel), as well as a more variable head positioning along the dorsoventral body axis ((c), right panel). (a-c) Pigeon silhouettes are approximately to scale.

Using the four calibrated high-speed camera views, three-dimensional positions of the LEDs were reconstructed in MATLAB within the 9 m³ volume covering the approach and obstacle forest (MathWorks, Natick, MA); [38]. Only flights in which the birds did not contact the obstacles were accepted for analysis. For every marker, the positional data were filtered, using a cubic spline filter with tolerances that resulted in marker speeds that most closely matched those obtained with a fourth-order, zero time lag Butterworth filter, using a low-pass cut-off frequency equal to the average wingbeat frequency. Raw positional data were smoothed with a cubic spline to avoid poor performance near the tails of the time-varying positional traces [39].

The three non-collinear body LEDs were used to define a body frame with orthogonal axes along the anatomical anteroposterior, AP, mediolateral, ML and dorsoventral, DV, axes. After expressing the wing markers in the body frame for each individual, a least-squares linear regression of all wing positions projected on the midsagittal plane was used to separate downstrokes from upstrokes: wings were defined to be in downstroke when wing marker velocities were directed anteroventrally in the direction of the regression trend line. If not, wings were defined to be in upstroke. Instead of defining wing amplitude as the one-dimensional angle between two extreme wing orientations, we used the integral distance travelled by a wing marker during each half stroke to define wing stroke amplitude. Similarly, the down/upstroke duration was the time a wing marker spent in down/upstroke, and wing speed was the average speed over the duration of down/upstroke. The stroke plane angle was defined as the angle between the AP axis and linear regressions of wing positions during down/upstroke projected on the midsagittal plane (figure 5b). We did not separate left from right wing to quantify these metrics for downstroke versus upstroke, as navigation past HOs is likely to be independent of contralateral asymmetries in wing kinematics. Wing extension was defined as the average Euclidian distance between the two wing markers at 50% duration of each half stroke.

To identify likely candidates for manoeuvring mechanisms used in negotiating HOs, we additionally determined stroke-to-stroke variability in amplitude, duration and speed as the standard deviation across all strokes, for each individual. Variability in wing extension was quantified as the average deviation in the mediolateral direction of the wing markers from the mean stroke trajectories (dark and grey lines in the frontal views in figure 5b,c). Similarly, variability in stroke path was quantified as the average deviation in the wing markers' sagittal plane motion relative to regression lines through all down/upstroke marker positions of each individual.

We applied a false discovery rate (FDR) controlling procedure [40] in multiple significance testing between NO and HO flights. Correlations between changes in potential and KE over the forest flight sections were tested with multiple least-squares linear regression models (JMP, SAS Institute, Cary, NC). These mixed-effect statistical models included a random effect of bird identity to correct for individual effects. We compared FDR adjusted p-values, p*, with a significance level of α = 0.05.

3. Experimental results

3.1. Characteristic features of horizontal obstacle flight

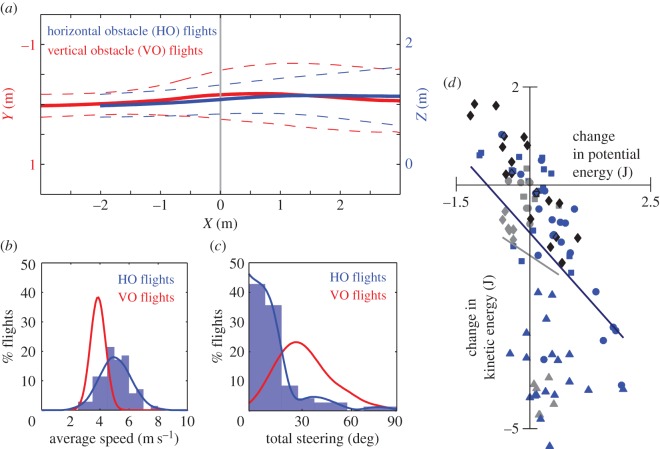
Despite the denser array of HOs, HO flights (blue, figure 2a) involved less steering by the pigeons in the XZ plane (87% of trials less than 30°) compared with VO flights (red) in the XY plane (87% of trials less than 60°). Overall, the mean trajectory for each set of obstacle flights matched the destination direction of the landing perch. As for VO flights, HO flights showed little evidence of path planning during the approach, with little or no evidence of steering until within 0.5–1.5 m of the obstacle field. Pigeons decelerated when approaching the obstacles (6.2 ± 1.1 m s⁻¹ greater than 1 m before versus 5.6 ± 1.0 m s⁻¹ within 1 m), but still flew past the HOs at higher speeds (5.0 ± 1.0 m s⁻¹) compared with VO flight speeds (3.9 ± 0.5 m s⁻¹; figure 2b). Steering was also more variable, as well as being substantially less strong, during HO flights compared with VO flights (figure 2c). For example, 42.8% of HO flights involved less than 10° of total steering whereas only 17.5% of VH flights had such low steering. Pigeons consistently traded off KE for PE and vice versa within the HO forest (multiple LS-regressions model: p < 0.0001; figure 2d). No such correlation was present for NO flights (p = 0.06). However, counter to our expectation, we did not observe a bias of converting KE to PE within the obstacle forest. PE changes were small compared with KE changes, and pigeons also converted PE to KE when flying through the HO field.

Figure 2.

Pigeons trade off potential and kinetic energy, but fly faster and steer less past horizontal obstacles (HOs) compared with vertical obstacle (VO) flights. (a) HO flights (blue) involved less steering in the XZ plane compared with VO flight navigation (red) in the XY plane (VO data originally reported in [34]). Overall, the mean trajectory for each set of obstacle flights matched the destination direction of the landing perch. As for VO flights, HO flights showed little evidence of path planning during the approach, with little or no evidence of steering until within 0.5–1.5 m of the obstacle field (dashed lines are s.d. of pooled traces). (b) Pigeons slowed down but flew past the HOs at a more variable and higher speed (5.0 ± 1.0 m s⁻¹) compared with VO flight speeds (3.9 ± 0.5 m s⁻¹). (c) Overall steering was also more variable as well as being lower in magnitude during HO flights compared with VO flights. For example, more than 40% of HO flights involved less than 10° of total steering. (d) Changes in potential energy (PE) relative to kinetic energy (KE) over flight sections within the HO forest were generally exchanged to conserve the pigeon's mechanical energy state (each shade of blue and symbol represents an individual; multiple LS-regressions model: p < 0.0001). No such trend was present for NO flights (grey symbols; p = 0.06). In the HO forest, however, PE changes were generally small and failed to show a bias for increased PE with decreased KE, indicating that in some trials the pigeons also steered down and increased flight speed in the forest.

Consistent with the reduced steering observed for horizontal navigation and the possibility that manoeuvring to navigate past HOs is less demanding, the frequency of obstacle contacts (determined across individual trials) with HOs (19.8 ± 3.5%, n = 4) was much less than the frequency of contacts with VOs (37.7 ± 13.6%, n = 3). Whereas 100% of VO contacts were made with one or both wings, only 8.7% of HO contacts were by the wings. The remainder resulted from contacts with the head, body, feet or tail of the bird. Obstacle contacts did not temporally cluster in earlier flights, and occurred with a variable distribution over HO flight trials.

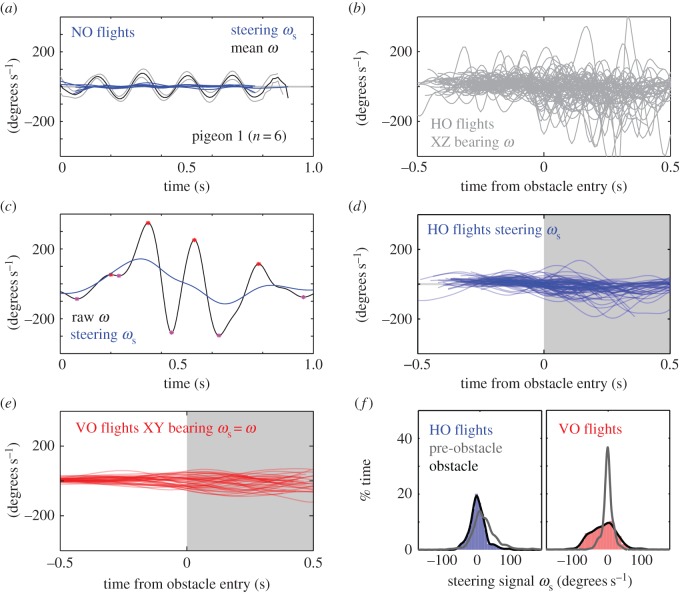
The pigeon's bearing angular velocity (ω) in the XZ plane fluctuated in a stereotypic sinusoidal pattern when flying without obstacles (figure 3a). When phase-corrected, all pigeons showed similar time-varying patterns of ω, with each pigeon having a unique frequency and magnitude. In these NO flights, the periodicity in head direction changes is possibly caused by oscillating pitch torques occurring at the wingbeat frequency [41]. A smoothing cubic spline filter was used to approximate the pigeon's steering signal (ω_s), which showed virtually no steering for non-obstacle flights (figure 3a). When negotiating HOs, ω fluctuated much more erratically (figure 3b). An overlay of all trials from the four pigeons for HO flights shows that some trials reached more than three times the amplitude of bearing ω compared with normal flights (figure 3b). One example HO trace (figure 3c) illustrates the substantial amplitude modulation as well as some frequency modulation of ω. Again, we can use the same cubic spline filter to extract the steering signal (ω_s). An overlay of all the approximated steering signals for HO flights (figure 3d) shows qualitative differences relative to the steering signals for VO flights (figure 3e). Whereas the steering for VO flights is smooth and persistent, the steering for HO contains transient large amplitude features. Although we observed little evidence of flight trajectory deviations prior to entering the obstacle field, the bearing angular velocity during the pigeon's approach for HO flights fluctuates more compared with no-obstacle flights shown in figure 3a. Distributions of steering signal prior to (grey) and during (black, shaded red) VO flight navigation show that steering dramatically increased when the pigeons entered the VO field (figure 3f, right). In contrast, the distributions of steering signal prior to (grey) and during (black, shaded blue) HO field navigation (right) differ much less (figure 3f, left).

Figure 3.

Determination of the pigeon's steering signal for horizontal versus vertical obstacle (VO) flights. The pigeon's steering signal (ω_s) was deduced from the head velocity direction (bearing) in the vertical, XZ plane. (a) The pigeon's head bearing angular velocity, ω, fluctuated in regular sinusoidal pattern during flights without obstacles, matching phase-corrected flight-averages of ω for each individual. A cubic spline-smoothing fit approximated changes in flight bearing with near zero steering for NO flights. (b) During HO flights, ω fluctuated more strongly and erratically (overlay of all trials; n = 74). During HO flights ω occasionally reaches >3× the amplitude of peak ω during NO flights. (c) One example HO trace demonstrates the high amplitude and frequency components of ω. We used a smoothing spline fit_, to approximate the steering signal (ω_s). (d,e) Whereas steering for VO flights is qualitatively smooth and persistent, the steering for horizontal obstacles (HOs) contains transient, large amplitude features (overlays of ω_s for HO and VO flights in blue and red, respectively). Although we did not observe flight trajectory deviations prior to entering the obstacle field, the bearing angular velocity during the pigeon's approach for HO flights fluctuates more compared with NO flights shown in (a). (f) Distributions of steering signal prior to (grey) and during (black, shaded blue) HO field navigation (left). Steering differed little when the pigeons entered the VO field. In contrast, the distributions of steering strength prior to (grey) and during (black, shaded red) VO field navigation (right) reflect a dramatic increase.

3.2. Head and wing motions during horizontal obstacle flight

A striking behavioural difference compared with non-obstacle flights was the presence of larger head speed fluctuations during obstacle flights (figure 4a–c). Head speed oscillated periodically, following a lower-frequency trend determined by the flight speed. Therefore, spline-filtered head speed containing only frequencies less than 50% wingbeat frequency were considered to represent flight speed. Relative head speed was determined by subtracting flight speed from global head speed. Relative body speed was similarly determined by subtracting the low frequency trend of body speed, obtained by spline-filtering the body speed with the same filter settings used to obtain flight speed, from global body speed. The mean ± s.d. (shaded areas) of individual mean cross-correlations of relative body speed with relative head speed for NO flights peaked at a time lag near 0 s (figure 4d, left panel), indicating synchronous relative head and body speed fluctuations when no obstacles were present. In contrast, during HO flights, fluctuations in relative body speed and relative head speed were nearly counter phase to each other (figure 4e, right panel). The autocorrelations of relative body and head speed contain periodic local maxima and minima near the wingbeat frequency, indicative of periodicity in both relative body speed and relative head speed (figure 4d). To quantify the relative head speed fluctuations, we computed the variability in global head speed as the mean rectified relative head speed. Head speed variability was consistently higher during HO flights than during NO flights for three-dimensional speed, as well as for each of the velocity components along the three corridor axes (figure 4f; all p* < 0.006). Variability in head speed was particularly pronounced in the X- (corridor fore–aft) and Z (vertical)-directions.

Figure 4.

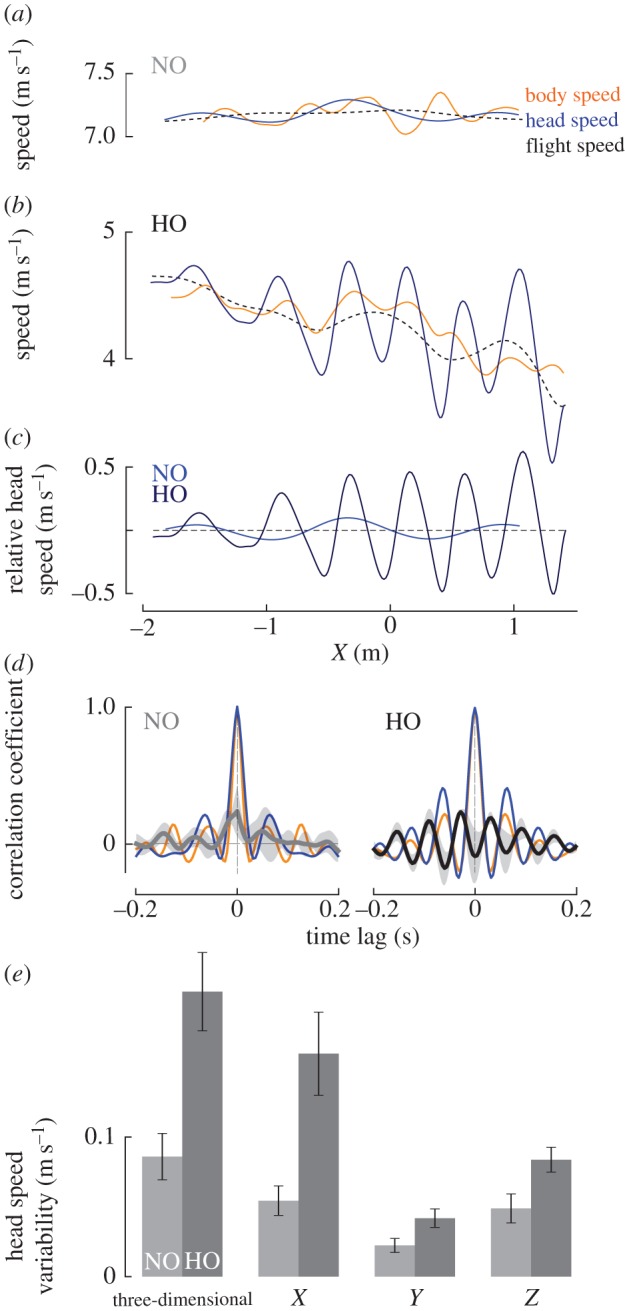
Pigeons bob their heads during obstacle flights, exhibiting larger head speed fluctuations in the presence of obstacles. (a,b) As illustrated by representative trials, head speed fluctuates more during HO flight compared with an NO flight (solid blue lines; light, NO; dark, HO flight). Head speed oscillates periodically, following a lower frequency trend determined by the pigeon's flight speed (dashed black lines). Body speed fluctuates at lower amplitudes and with no clear phase-relation to head speed. (c) Relative head speed, determined by subtracting flight speed from global head speed, oscillates more strongly during HO flight compared with NO flight, particularly near and within the HO forest (X > 0 m). (d) The mean ± s.d. (shaded areas) of individual mean cross-correlations of relative body speed with relative head speed for NO flights peaks at a time lag near 0 s (grey line, left panel), indicating synchronous relative head and body speed fluctuations when no obstacles are present. In contrast, during HO flights (right panel), fluctuations in relative body and head speeds are nearly counter-phase. The autocorrelations of the body and head (orange for body, blue for head) contain periodic local maxima and minima, indicating periodicity near the wingbeat frequency. (e) Head speed variability, based on the mean rectified relative head speed, is higher during HO flights than during NO flights for three-dimensional speed, as well as for individual velocity components along the three corridor axes (all p* < 0.006). Head speed fluctuations are particularly pronounced in the fore–aft and vertical directions.

Together with increased variability of global head speed during HO flights, we also observed a significant increase in translational head movements relative to the body during HO flights compared with non-obstacle flights, with the envelope of head positions and its variability increasing more than twofold in the anatomical dorsoventral direction across individuals (p* = 0.015; table 2 and figure 5b,c). Both increased global head speed variability and relative head translational movements indicate the same increase in head-bobbing-like movements during HO flights when compared with NO flights.

Table 2.

Variability of local head positioning. Mean ± s.d. of individual variability of head position. Significant differences between NO and HO flights are in italics.

	variability along AP (cm)	variability along ML (cm)	variability along DV (cm)
NO flights	0.64 ± 0.59	0.88 ± 0.24	0.77 ± 0.15
HO flights	1.15 ± 0.61	0.75 ± 0.12	1.56 ± 0.44

In addition to increasing head movements, the pigeons also altered particular wing kinematics parameters while negotiating the HO forest. To account for variation in marker placement among individuals, local wing kinematics were normalized to the individual downstroke means during NO flights (table 1; for non-normalized values, see electronic supplementary material, table S1). To navigate past the HOs, the pigeons tilted their wing stroke plane backward by increasing the anterior sweep of the wings, compared with the stereotypic pattern of wing movements during non-obstacle flight and while approaching the obstacles (table 1; p* = 0.005 for upstroke and downstroke). They also reduced downstroke and upstroke wing extension (table 1; p* = 0.013 and 0.016, respectively), compared with NO flight. Lastly, HO manoeuvres were associated with more variable wing extension (p* = 0.045 and 0.002 for downstroke and upstroke, respectively) and wing path (p* = 0.001 for downstroke and upstroke; table 3 and figure 5b,c) movements. Overall, averages of wing stroke amplitude, duration and thus, wing speed, however, did not differ between NO versus HO flights (table 1); nor were these metrics more variable in the HO forest (table 3).

Table 3.

Stroke-to-stroke variability of local wing kinematics. Mean ± SD of individual variability of wing kinematics. Significant differences between NO and HO flights are in italics.

	variability in stroke amplitude (cm)	variability in stroke duration (ms)	variability in wing speed (m s−1)	variability in wing extension (cm)	variability in stroke path (cm)
downstroke
NO flights	8.4 ± 1.1	17 ± 4	0.3 ± 0.0	2.1 ± 1.5	3.4 ± 0.5
HO flights	9.6 ± 0.9	13 ± 2	0.6 ± 0.2	4.9 ± 0.7	6.0 ± 0.3
upstroke
NO flights	8.3 ± 0.7	15 ± 5	0.3 ± 0.1	2.2 ± 0.5	3.1 ± 0.2
HO flights	9.3 ± 0.8	14 ± 1	0.4 ± 0.2	4.2 ± 0.3	4.6 ± 0.3

3.3. Guidance modelling results

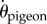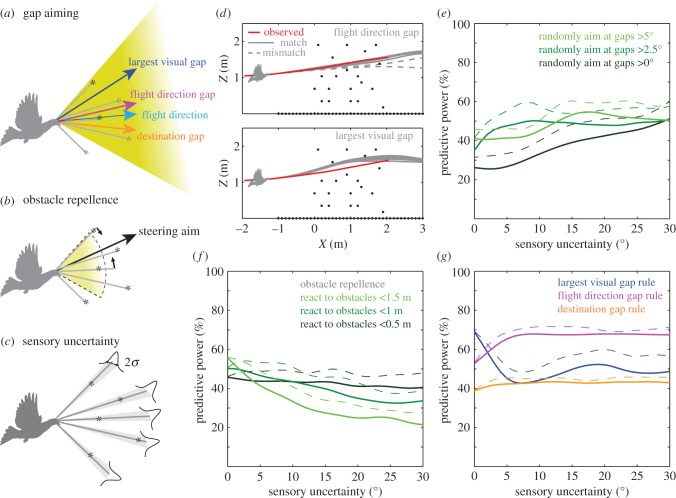
We have shown previously that pigeons navigating past VOs can be modelled as a proportional controller with a fixed delay [34]. For the purpose of comparing VO and HO flights, we used the same proportional controller (gain = 4.7 s⁻¹, delay = 134 ms) to compute the predictive power of each guidance rule as a function of sensory uncertainty. The pigeon's bearing angular velocity served as the control variable, which evolved the flight trajectory over time. The model applied a corrective term to 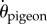as a function of the deviation from the ideal steering aim. The ideal steering aim was determined by a choice of gap given 134 ms prior to the moment of steering correction. Three gap-aiming rules were evaluated: largest gap, flight direction gap and destination gap (figure 6a). These gaps were evaluated within a ± 30° ‘attention zone’ (yellow-shaded cone, figure 6a,b), which matched the prior maximal steering range that was observed for pigeons during VO navigation. As a reference, we also implemented an obstacle avoidance model that drove the pigeon's steering aim away from obstacles within a given range (figure 6b). Specifically, each ‘in-range’ obstacle contributed an aim bias, and the sum of all these biases determined the ideal aim for the pigeon for this steering strategy.

Figure 6.

Aiming for gaps most aligned with the flight direction best predicts the observed limited steering past horizontal obstacles in the pigeon. The pigeon's guidance strategy was evaluated by simulating four simple steering rules given observed initial conditions. (a) Following the gap-aiming paradigm that we introduced in previous work [34], we categorize gaps between obstacles (denoted by asterisks) based on their angular size and position: largest visual gap, flight direction gap and destination gap. Gaps are considered within a ±30° attention cone (yellow shading) over a range of 1.5 m (the maximum steering and reaction distance we observed for vertical obstacle navigation). Our model assumes that the pigeon steers towards one type of gap throughout its obstacle flight. (b) As a reference, we implemented an obstacle repellence model [35] in which each obstacle within a certain range contributes to the steering aim of the pigeon. The pigeon's steering aim results from the weighted contribution of all obstacles within this range. (c) In reality, animals can never perfectly measure obstacle positions. We simulate this sensory uncertainty by introducing Gaussian noise, with a tunable standard deviation. (d) Given a sensory uncertainty of 5°, the model pigeon generates different trajectories from the same initial conditions. Some trajectories match the observed trajectory (solid grey lines) and some do not (dashed grey lines). Here, we show one particular trial simulated by two different gap-aiming rules. By repeating the simulation 50 times, we quantify the predictive power of a specific guidance rule. (e) To establish a baseline for the predictive power of different steering rules, we first simulate randomly chosen gaps given a minimum gap size threshold. The average predictive powers (solid lines) for all three conditions are below 50% given zero sensory uncertainty. As sensory uncertainty increases, the random gap selection simulations converge to 50%, with the maximum predictive powers (dashed lines) approaching 60%. (f) The obstacle repellence model has average predictive powers (solid lines) close to 50% at zero sensory uncertainty but degrades quickly as sensory uncertainty increases, particularly when guided by more distant obstacles. A similar trend is observed in maximum predictive powers (dashed lines). (g) The largest visual gap rule (blue) exhibits the highest predictive power at zero sensory uncertainty, but drops quickly with as little as 5° sensory uncertainty. The flight direction gap rule (magenta) is most robust and maintains predictive power close to 70% from 5° to 30° sensory uncertainty. The destination gap rule (orange lines) never predicts more than 50% of the flights. The flight direction gap rule maximally predicts the actual flight trajectories by just over 70% (pink dashed line). (Online version in colour.)

In reality, any visual system has sensory noise, which degrades the exact knowledge of the obstacle angular position. We simulated this sensory uncertainty by replacing the angular positions of the obstacles by a random sample from a Gaussian distribution centred at the actual obstacle position (figure 6c). Two example sets of simulated flights (grey traces) relative to the observed flight trajectory (red trace) are shown based on the flight direction rule and the largest gap rule (figure 6d), given a sensory uncertainty of ±5°. Owing to the random uncertainty of the obstacle location, the simulated pigeon trajectories may bifurcate from the same initial condition. Thus, some simulated trials will match the observed trajectory, whereas some will not (solid versus dashed grey lines, figure 6d). By running the simulation 50 times per trial across many trials, we quantified the percentage of successful trajectory reconstruction (predictive power) for each steering rule, both on average and at a maximum level.

By changing the level of sensory uncertainty (figure 6c), we evaluated how the predictive power changes for each steering rule as a function of increasing sensory uncertainty. When the sensory uncertainty is zero, the flight trajectory is deterministic and the predictive power is fixed. As a result, the modelled simulations cannot accommodate any subtle degeneracy of the flight trajectory (e.g. if two gaps have practically the same quality, then the model and the real pigeon could pick different gaps despite having the same guidance strategy). At the other extreme, when the sensory uncertainty approaches 30°, the simulated pigeon essentially cannot determine the location of any particular obstacle within its ±30° ‘attention zone’.

In carrying out these simulations, we first found that randomly steering to gaps of a given angular threshold within the ±30° attention zone results in predictive powers less than 50%, all of which converge to 50% when sensory uncertainty reaches 30° (figure 6e). This established a baseline from which we can evaluate the predictive performance of other steering rules. The fact that randomized ‘blind’ steering still accounts for half of the flight trajectories indicates that the pigeons did not exhibit much steering. On the other hand, if the simulated pigeon were to steer away from all obstacles within a certain range from its current position, then the predictive power of obstacle avoidance is generally only as good as randomly aiming to a gap with zero sensory noise; as sensory uncertainty increases, the predictive power of obstacle avoidance decreases further (figure 6f).

In contrast, if the simulated pigeon steers towards the largest visual gap within its attention zone (blue trace, figure 6g), then 70% of observed flights are accurately recapitulated with zero sensory uncertainty. However, as sensory uncertainty increases, predictive power quickly drops below 50% and does not substantially improve with a further increase in sensory uncertainty. If the simulated pigeon steers towards the gap most aligned with its flight direction (or bearing), predictive power increases from 54% (zero sensory uncertainty) to nearly 70% as sensory uncertainty reaches 5° (magenta trace, figure 6g). Notably, predictive power plateaus and remains stable for this gap-aiming rule as sensory uncertainty increase up to 30°. This suggests that pigeons may have a strong steering bias towards maintaining their flight direction, regardless of other visual cues. Finally, steering towards gaps most aligned to the pigeon's destination direction results in uniformly low (approx. 43%) predictive power (orange trace, figure 6g).

Overall, these results suggest that a gap-aiming behaviour better describes pigeon steering to navigate HOs than does an obstacle repellence model, and that steering to gaps most closely aligned with the bird's current flight direction best predicts observed flight trajectories.

4. Discussion

Speeding through a cluttered environment is an extreme sensorimotor challenge, which reduces sensory accuracy and limits computational resources by imposing a time pressure, while simultaneously increasing the cost of failure through the potential of high-speed collisions. We have shown that pigeons can fly through obstacle arrays of both vertical and horizontal orientations while maintaining relatively high speed. They achieve this by employing simple visual heuristics and by tolerating minor contacts with the obstacles. Specifically, while pigeons slowed down and steered towards the largest visual gap between VOs, when flying past HOs they maintained higher speed and preferred gaps that were more aligned to their flight direction, despite a denser obstacle arrangement. Both these gap-aiming strategies are supported by flight guidance work showing that bees [42] and budgerigars [11] adjust their flight path and speed to balance left versus right optic flow, as steering to a gap essentially balances the angular motion of obstacles to either side of the gap.

To navigate HOs, pigeons adopted several behavioural modifications, which may have important sensory and motor implications. Tilting the wing upstroke plane backward is a signature of a tip-reversal upstroke that enhances the ability to generate extra lift [43] at slower flight speeds. The pigeons also actively increased horizontal fore–aft and vertical translational movements of their head when flying through HOs, which could engage motion vision mechanisms (e.g. motion parallax, hyperacuity) or visually stabilize some obstacles (e.g. bar fixation). Whether such head motion truly serves a visual function and what function remain unclear and will require future investigation.

4.1. Flight differences for navigating horizontal versus vertical obstacles

To negotiate close-range obstacles of either vertical or horizontal orientation, the pigeons exhibited a reactive approach to navigation, with little evidence of prior path planning following perch takeoff. Little, if any, steering was observed until the pigeons were within 0.5–1.5 m of the obstacle field (figure 3a). Although the pigeons consistently slowed down during their approach to the obstacle fields, they flew significantly faster past the HOs than they did past VOs (figure 3b). Even though the vertical pole obstacles were thicker, the HOs were more densely distributed with a larger number of obstacles. Overall, obstacle density likely has a stronger effect on manoeuvring requirements than obstacle dimensions, as most of the required steering to avoid obstacles is determined by the dimensions of the body part that needs to avoid the obstacle, rather than the small (extra) width of (vertical) obstacles.

We hypothesized that pigeons would trade-off reduced KE with increased PE, biasing their flight paths upward (+Z) to facilitate HO navigation; however, we found no evidence of this. Although overall changes in PE were small, when PE decreased a significant increase in KE was observed and vice versa (figure 2d). Flying through HOs seems less challenging than flying through VOs. Consistent with this, there was a substantially greater incidence of vertical (38% of flights) than horizontal (20%) obstacle contacts, in which 100% of VO contacts were with the wings, versus only 9% for HOs. The high incidence of wing (and body) contacts that we observed indicates the challenging nature of the experimental designs. In fact, we initially challenged pigeons to fly through even denser distributions of HOs (7.5 obstacles m⁻²), but none of the birds managed to fly through. Nevertheless, pigeons were highly successful in executing both sets of obstacle navigation flight trials, consistent with their ability to fly through extremely narrow spaces [21]. Clearly, a limitation of our experimental design is that the HOs were of a different size and spacing density compared with the VOs, limiting direct comparisons between the two sets of experiments.

The observed higher flight speeds, fewer obstacle contacts and more limited steering suggest higher agility in vertical manoeuvring past HOs. This higher agility is likely based on the greater control authority that birds and other flapping animals have for producing aerodynamic force in the vertical direction to support their weight. Further, whereas VOs often require birds to pause their wings at stroke reversal [21,22], limiting the aerodynamic force that the wings can generate while in this position, pauses in the wingbeat cycle can occur at mid-downstroke, with the wings held in a gliding posture that allows effective aerodynamic force generation, to facilitate HO manoeuvring. Although HO manoeuvring may be less challenging than VO navigation with respect to flight aerodynamics, the pigeons still needed to steer clear of obstacles and/or reduce the vertically projected area swept by the wings, to reduce wing contacts with the obstacles (figure 5a). As a result, pigeons exhibit more variable wingbeat patterns when negotiating HOs when compared with the highly stereotypic patterns observed for non-obstacle flight (figure 5b versus c).

4.2. Behavioural adjustments associated with horizontal obstacle flight

As expected, we observed significant adjustments in wing stroke kinematics as pigeons navigated through the HO field. The pigeons tilted their wing stroke plane backward by increasing the anterior sweep of the wings and reduced their mid-stroke wing extension in comparison with the stereotypic patterns of wing movements observed during non-obstacle flights (table 1). Increased variability in wing extension and stroke paths were also observed in both downstroke and upstroke during HO manoeuvring (table 3 and figure 5b,c), despite the fact that overall averages of wing stroke amplitude, duration and wing speed did not differ between NO versus HO flights. Manoeuvring through a HO forest involves mostly vertical flight path changes. Steering up or down likely involves modulation of body pitch, and thus the generation of pitch torques [44]. It is difficult to infer torque-generating mechanisms from changes in mean wing kinematics and their variability, between level flight and vertical manoeuvring flight past HOs. However, the observed changes in stroke plane angle, particularly more anteriorly swept wings, likely relate to shifting the centre of aerodynamic pressure anteriorly and dorsally, later in downstroke and early in upstroke, to produce a pitch-up torque. Similarly, changes in wing stroke trajectories produce roll torque in pigeons during turning flight [41].

A surprising behavioural modification during obstacle flight was the increase in head speed fluctuations (figure 4a,b,e). Cross-correlations between relative head speeds and relative body speeds suggest independent modulation of the head, and not a simple mechanical coupling between the head and the body. In the global frame of reference, we observed significantly greater vertical head-bobbing-like movements relative to the pigeon's body during HO flights compared with non-obstacle flights (figure 5b versus c). The greater than twofold increase in dorsoventral head motion has the potential to enhance motion parallax, which can be used in depth perception of the HOs. Alternatively, the increased head movements could serve to stabilize the obstacle image on the retina, which may aid depth perception through improved measurement of relative velocity [45]. The observed obstacle-dependent head movements are similar to the head-bobbing observed in pigeons prior to landing and reminiscent of the head-bobbing observed during walking in many bird species, both of which are thought to serve a primarily visual function [46–49]. The absence of clear head-bobbing in non-obstacle flights is consistent with a lack of head-bobbing during take-off flight [46].

4.3. Strategic differences in horizontal versus vertical obstacle flight navigation

Clear strategic differences were observed for pigeon flight navigation through horizontal versus VOs. Notably, while the VO flights can be well described by steering to the largest visual gap [34], HO flights are best modelled as steering to the gap most aligned to the current flight direction. This shift of steering preference is likely due to biomechanical constraints and aerodynamic differences associated with flying past horizontal versus VOs. In order to steer past VOs, pigeons must find an opening that allows them to clear both wings sufficiently. Thus, large gap sizes seemed to be preferred. In contrast, pigeons can fit through much narrower horizontal openings given that they can coordinate the wing posture properly. As a consequence, they appear to simply aim for the gap closest to their current flight direction. It is interesting, however, that the largest gap rule outperforms the flight direction gap rule given low sensory uncertainty. In fact, the 70% predictive power of steering to the largest visual gap between HOs at zero uncertainty is comparable to the predictive power for the same gap selection rule for VO flights [34]. It, therefore, seems likely that a bird may simultaneously assess available gap sizes for clearance consideration and their alignment to the bird's current bearing for biomechanical convenience. In our modelling approach, we tested each steering strategy independently, but there is no reason why a bird should not and could not apply both strategies at the same time. Although it is unclear if and how these two strategies are integrated during other flight manoeuvring behaviours, our modelling results for both vertical and HO flight navigation suggest that the relative importance of gap size for steering control is a function of obstacle orientation and perhaps flight speed.

Reactive navigation through both horizontal and VOs is also better described by gap aiming rather than by obstacle repellence. Obstacle repellence has been a useful way to model route selection to negotiate a small number of obstacles [29,35]. However, summing up the repellent contributions from all obstacles could lead to conflicting steering signals. For faster movement through a large number of obstacles, a gap-aiming strategy performs much better. Fundamentally, by steering away from obstacles rather than towards an available gap, there is no knowledge of what regions of the cluttered environment are obstacle-free. For this reason, gap-aiming is a more comprehensive and likely successful approach for attempting to create obstacle negotiation heuristics, especially for large numbers of obstacles.

4.4. Relevance to guidance of bioinspired autonomous aerial systems

Our previous [21,34] and current studies of pigeon obstacle flight suggest that flying animals employ two general strategies to negotiate obstacles at high speed: visual heuristics and collision tolerance. How can these inspire new control schemes for UAS? ‘Reactive autonomy’ incorporates obstacle avoidance, and is the most active area of guidance control research in aerial robotics [2]. Visual heuristics provide fast alternatives to conventional map-based approaches and are commonly found in animal navigation. To date, the most reliable flights through cluttered environments are only observed in flying animals or drones piloted remotely by a human via non-stereo visual feedback (exemplified by the increasingly popular sport of drone racing). While extracting visual heuristics from flying animals enables discovery of efficient control schemes for obstacle negotiation, it might similarly be fruitful to extract visual heuristics of human steering strategies for UAS, as has been recently attempted [50]. Finally, collision tolerance, which birds and other flying animals achieve well, is also being explored in the aerial robotics community [51,52]. Consequently, we expect that parallel investigation of obstacle flight guidance from both experimental biology and control engineering will continue to contribute key insights for successfully realizing autonomous robots that move among and around us.

Data availability

Data are available at: https://figshare.com/s/667dbcb6a65adf7b249e.

Authors' contributions

I.G.R., H.T.L. and A.A.B. conceived the study. I.G.R. and A.A.B. designed the study. I.G.R. and P.S.B. performed the experiments and processed the data. I.G.R. performed the statistics and analyses for the behavioural modification. H.T.L. performed the analyses comparing V.O. and H.O. flights, and implemented the flight guidance models. I.G.R., H.T.L. and A.A.B. wrote the manuscript with critical input from P.S.B.

Competing interests

We declare we have no competing interests.

Funding

This research was supported by a grant from the Office of Naval Research (ONR, N0014-10-1-0951) to A.A.B.