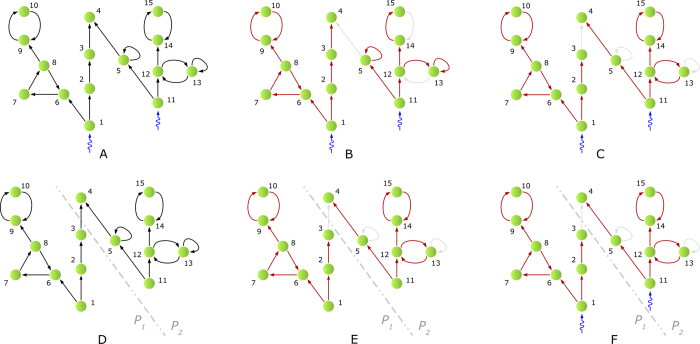
Figure 2. Actuation Spectrum.

Figures (A–C) depict the actuation spectra of three networks with N = 100 nodes using a heat-map with colors ranging from yellow to red, where yellow (respectively, red) corresponds to a low (respectively, high) number of driving nodes (denoted by 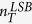) or driven nodes (denoted by 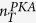) required to control the network in at least T time steps (represented in the x-axis using the scale log₁₀₀(T)). Notice that the highest number of driving/driven nodes (darkest red) is required when T = 1 (or, log₁₀₀(T) = 0), since we need to actuate all the nodes to drive the network state in a single time step (i.e., ). Similarly, the lowest number of driving/driven nodes (brightest yellow) is achieved in the absence of time constraints (i.e., T = 100 or log₁₀₀(T) = 1). In addition, we mark by vertical dashed lines the values of log_N (T) for which the number of required driving/driven nodes corresponds to 25%, 50% and 75% of the network size N. The three networks under consideration exhibit qualitatively different decays in the number of driving/driven nodes as T increases. In particular, the faster the decay in the actuation spectrum, the easier it is to control the network in a short time window. We, therefore, say that a network is ‘agile’ if its actuation spectrum decays fast as a function of T. In this sense, the Type-III network in (C) is the most ‘agile’, while the Type-I in A is the least ‘agile’. Notice how the actuation spectrum of an ‘agile’ network decays fast to the yellow level in the heat-map, or, equivalently, the vertical dashed lines are shifted to the left.