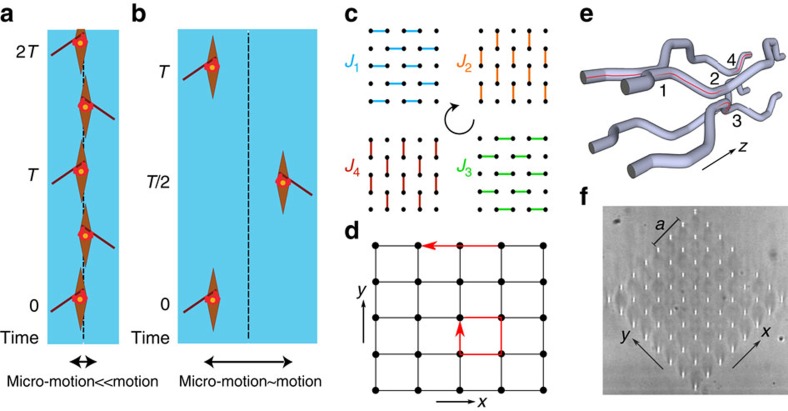
Figure 1. Slowly driven systems and photonic implementation.

Sketch illustrating the high-frequency regime (a), and away from the high-frequency regime (b), for a simple driven system, here represented by a rower. In the high-frequency regime, the micro-motion typically only slightly affects the motion: the time evolution is well captured by time-averaged dynamics, which can be probed stroboscopically at discrete times Δ_t=T × integer. Away from the high-frequency regime, the micro-motion can significantly affect the dynamics, and the time evolution is no longer well described by the time-averaged Hamiltonian only. (c) The four different bonds present in the lattice (with coupling constants J_1,2,3,4) and the cyclic driving protocol employed. (d) In the simplest case where all bond strengths are equal, JT/4=π/2, chiral edge modes arise, while the bulk is localized (the evolution operator over one period of the drive is trivial (identity) in the bulk). (e) Sketch illustrating how, using ultrafast laser inscription, different pairs of waveguides can be moved together to turn on a coupling and then apart to switch it off. Within the paraxial approximation, this flexibility allows for a realization of the driving protocol shown in c. In waveguide arrays, the propagation direction z plays a role analogous to time³⁶. (f) White-light transmission micrograph of the facet of the laser-fabricated photonic lattice. Note that the axes of the photonic lattice were rotated by 45° with respect to the vertical to obtain equal coupling constants along the two axes (ref. ³⁷). Here a is the lattice constant.