On identifying kinematic and muscle synergies: a comparison of matrix factorization methods using experimental data from the healthy population

Literature on comparing factorization methods in identifying motor synergies using numerically generated, simulation, and muscle activation data from animal studies already exists. We present an empirical evaluation of the performance of three of these methods on muscle activation and joint angles data from human reaching motion: principal component analysis, nonnegative matrix factorization, and independent component analysis. Using numerical simulation, we also studied the meaning and differences in the synergy structures returned by each method. The results can be used to unify approaches in identifying and interpreting motor synergies.

Abstract

Human motor behavior is highly goal directed, requiring the central nervous system to coordinate different aspects of motion generation to achieve the motion goals. The concept of motor synergies provides an approach to quantify the covariation of joint motions and of muscle activations, i.e., elemental variables, during a task. To analyze goal-directed movements, factorization methods can be used to reduce the high dimensionality of these variables while accounting for much of the variance in large data sets. Three factorization methods considered in this paper are principal component analysis (PCA), nonnegative matrix factorization (NNMF), and independent component analysis (ICA). Bilateral human reaching data sets are used to compare the methods, and advantages of each are presented and discussed. PCA and NNMF had a comparable performance on both EMG and joint motion data and both outperformed ICA. However, NNMF's nonnegativity condition for activation of basis vectors is a useful attribute in identifying physiologically meaningful synergies, making it a more appealing method for future studies. A simulated data set is introduced to clarify the approaches and interpretation of the synergy structures returned by the three factorization methods.

NEW & NOTEWORTHY Literature on comparing factorization methods in identifying motor synergies using numerically generated, simulation, and muscle activation data from animal studies already exists. We present an empirical evaluation of the performance of three of these methods on muscle activation and joint angles data from human reaching motion: principal component analysis, nonnegative matrix factorization, and independent component analysis. Using numerical simulation, we also studied the meaning and differences in the synergy structures returned by each method. The results can be used to unify approaches in identifying and interpreting motor synergies.

the human central nervous system (CNS) plans and executes smooth and well-coordinated motor behaviors with ease, despite facing multiple levels of challenges such as redundancy in the human musculoskeletal system, noisy sensory input, and complexity (i.e., nonlinearity and time dependency) of the biomechanics of the body. Understanding how the CNS overcomes the computational burden of motor control has been a focus of the field of human motor control and motor learning (Guigon 2010).

Human motor behavior is highly goal directed. This requires the CNS to coordinate different aspects of motion generation to achieve the motion goals (Turvey 1990). Using the terminology introduced by Latash and Anson (2006), the CNS organizes the control of elemental variables to stabilize performance variables. For example, in studying reaching in three-dimensional (3D) space, the rotation of each of the arm joints [arm's degrees of kinematic freedom (DOF)] or activation of each of the arm muscles (arm's muscular DOF) or joint torques (arm's DOF) can be considered as an elemental variable. To this end, an elemental variable is the smallest unit that can describe the musculoskeletal system at the chosen level of analysis. Continuing with the example of three-dimensional reaching, the position of the tip of the index finger or the orientation of the hand can be a performance variable depending on the goal of reaching (e.g., pointing vs. grabbing a glass of water). Performance variables are directly related to the task goal and present the most important outcomes of the motion.

The concept of motor synergies (i.e., muscle or kinematic synergies) provides an approach to quantify the covariation of the elemental variables during a task. A motor synergy can be defined as a set of stable spatiotemporal patterns of activity shared across elemental variables that leads to a desirable performance variable (McMorland et al. 2015). Recent studies, among different models of motion generation, suggest that the CNS may generate motor commands through a linear combination of motor synergies, each controlling a group of elemental variables (Santello 2002; Freitas et al. 2006; Cheung et al. 2012; Alessandro et al. 2013; Bizzi and Cheung 2013; Berger and d'Avella 2014; Tamei et al. 2015; Federolf 2016). Such coactivation of elemental variables leads to a reduction in the dimensionality of the motor control. Based on this definition, by the scaling and time shifting of a small set of covariation patterns, the entire set of muscle or joint variations during task performance can be generated (d'Avella et al. 2003).

To quantify motor synergies, dimensionality reduction methods (Tresch et al. 2006) are readily available to analyze large sets of muscle activity or joint angle changes observed over the course of motor tasks. Several recent studies have demonstrated that a range of functional tasks can be explained by motor synergies. These studies have shown that between 75 and 90% of the variance in the EMG measured during unilateral reaching (Muceli et al. 2010; d'Avella and Lacquaniti 2013; Azaripasand et al. 2015), balance (Torres-Oviedo and Ting 2010), grasping (Vinjamuri et al. 2014; Tagliabue et al. 2015), gait (Hagio et al. 2015), visuomotor adaptation (Gentner et al. 2013), and unilateral isometric force generation (Roh et al. 2015) can be explained by combinations of muscle synergies. Similarly, studies have shown that a low-dimensional space accounts for a large portion of the kinematic variance in a range of tasks such as unilateral reaching (Braido and Zhang 2004), typing (Soechting and Flanders 1997), grasping (Tagliabue et al. 2015), and multidigit force generation (Jae et al. 2005).

One of the critiques of these studies is that the synergies they report are task specific and might be reflecting the biomechanical constraints of the task rather than the underlying neural strategies of motor control (Rearick et al. 2003; Todorov and Ghahramani 2004; Tresch and Jarc 2009; Steele et al. 2015). For example, a tabletop reaching task while the torso is restrained (Dipietro et al. 2007) reduces the redundancy of joint motion patterns that can be identified as a kinematic synergy.

To address this main critique, this study is focused on quantification of motor synergies demonstrated during exploratory motor tasks instead of goal-directed motor tasks with physical constraints. Specifically, we studied exploring a task space parallel to the frontal plane using symmetric bimanual reaching motions, i.e., the two hands move synchronously in horizontal and vertical directions. This task presents two main advantages. First, with the removal of constraints imposed by the task's goal (reaching to specific targets), the apparent reduction in the redundancy of the joint space will be removed (Thakur et al. 2008). Moreover, the requirement to execute symmetric bimanual motions is a natural tendency in the activities of daily living (Kelso 1984; Steenbergen et al. 1996; Vinjamuri et al. 2008) and will not be viewed as a constraint imposed by the task. Second, the way humans execute an exploratory task is a function of their own biomechanical constraints (McDonald et al. 1995) and motor control strategies. This means that analyzing the motion patterns of an individual during an exploratory task has the potential to reveal individualized motor control strategies and deficits (Huang and Patton 2013; Lancaster et al. 2014; Valdés et al. 2015).

Although several studies support the motor synergies hypothesis, they have used several different computational methods to provide this support by identifying underlying synergies in human motor behavior. A range of factorization methods has been used in these studies to reconstruct the experimental data by linearly combining a small set of basis vectors or motor synergies. Tresch et al. (2006) empirically compared performance of six matrix factorization methods using numerically generated and experimental data from frogs. In a recent study, Steele et al. (2015) compared the performance of the factorization methods in Tresch et al. (2006) using muscle activation data generated from a musculoskeletal software model. Building on this work, we present an empirical evaluation of the performance and robustness of three factorization methods on human reaching motion data (muscle electromyography and joint angles). The three methods considered in this paper are principal component analysis (PCA), nonnegative matrix factorization (NNMF), and independent component analysis (ICA). Although similar in their general approach, these factorization methods return different synergy structures, as they utilize different algorithms. Using numerical simulation, we also studied the meaning of the synergy vectors returned by each of the factorization methods. This will inform how synergy vectors can be interpreted by motor coordination researchers.

The results presented in this article can be used to expand our understanding of the robustness and numerical interpretation of the methods used in motor synergy research, building a common ground for understanding “healthy” motor coordination. This knowledge leads to an understanding of the effects of different motor deficits on motor synergies and the nature of motor recovery and, ultimately, creating individualized care for physical therapy clients.

METHODS

Research ethics and study participants.

Fifteen healthy adults were recruited and provided written consent to take part in this study. The average age of the participants was 24.8 ± 3.5 yr. The male to female ratio was 8/7. This study was approved by University of British Columbia's Clinical Research Ethics Board.

Experiment setup, data collection, and preprocessing.

The motion-controlled gameplay system developed under the FEATHERS project (Functional Engagement in Assisted Therapy through Exercise Robotics) was used in this study. This project aims to provide an engaging solution for physical therapy for adults poststroke or teens with cerebral palsy by combining bilateral movements with computer games on a social media platform (Valdés et al. 2014; Shirzad et al. 2015). The system uses data read from a Microsoft Kinect to map the user's bilateral hand motions in the frontal plane to the motion of a cursor on the screen. Specifically, at a 30 frames/s rate, the 3D displacements of both wrists are compared at every time step to ensure that the hand motion with the least movement in the user's frontal plane is mapped into cursor motion. The user then can play simple video games using the cursor's motion. The participants were instructed to keep their hands at least 10 cm apart from each other as they used the system.

Each participant took part in one data collection session in which he or she was asked to complete a set of tasks to gain familiarity with the FEATHERS system and a game called “Lucky Pirate” (OUAT Entertainment). This game is set on a static background and requires players to explore the entire game screen to select and click on treasure chests that may contain gold coins. To promote engagement, the game provides visual and auditory feedback when the user opens a new treasure chest or completes a level. In addition, the user can obtain special items from the chests to extend game play. Completion of a level does not carry a time restriction; as a result, users are able to progress at their own pace. Retrieval of different items did not lead to any external rewards for the participants. At the end of the data collection, each participant was given a $10 coffee shop gift card to thank them for his or her time.

The game and the system are designed to provide a virtual reality-based motor exploration task (Valdés et al. 2015; Lambert-Shirzad and Van der Loos 2016). To avoid recording task-specific synergies that reflect the task's biomechanical constraints rather than the underlying neural strategies of motor control (Rearick et al. 2003; Todorov and Ghahramani 2004; Tresch and Jarc 2009; Steele et al. 2015), participants' reaching motions are made exploratory by removing task space constraints. This includes 1) presenting the participant with a variety of targets rather than presenting them with a goal-directed reaching toward a specific target, and 2) asking the participant to perform freehand reaching motions in a 3D task space rather than two-dimensional (2D) table-top reaching and/or holding on to a manipulandum. The requirement to use both hands to move the cursor on the screen is not considered a limiting physical constraint as the participants are free to choose how they want to temporally and spatially synchronize the motion of their hands. Moreover, the use of both hands at the same time does not impose any constraints in the joint and muscle spaces, letting the participants demonstrate and use separate joint/muscle space strategies (kinematic and muscle synergies) to generate the motions.

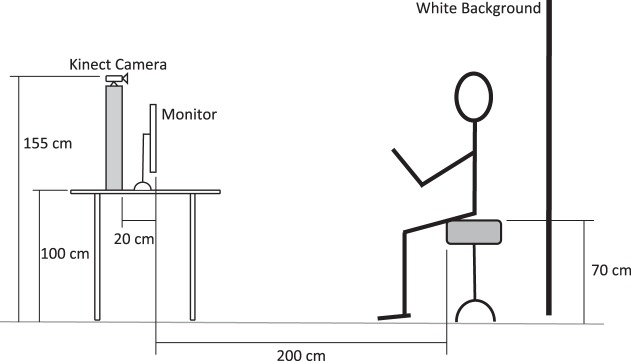
The participants were asked to sit on a 70-cm tall stool without a back support, two meters away from a flat screen monitor (Fig. 1). The Lucky Pirate gameplay screen was projected on the monitor and participants played the game by controlling a magnified cursor on the screen. The motion of the participant's wrists was captured via a Kinect camera and was used by the FEATHERS software to move the cursor on the screen.

Fig. 1.

A schematic of the experiment setup.

After gaining familiarity with the task, the participants were asked to play the game for at least 5 min while whole body motion data and muscle electromyography (EMG) data were collected. The Microsoft Kinect motion capture system was used to collect joint kinematics data (Choppin and Wheat 2013; Webster and Celik 2014). The Kinect tracked the Cartesian location of several anatomical landmarks by assigning markers to them: center of hip, chest at the level of the shoulders, shoulders, elbows, wrists, and hands. A 16-channel Delsys (Natick, MA) EMG system recorded muscle activation from 8 muscles on each side of the body: the brachioradialis, biceps brachii, triceps brachii (long and lateral heads), deltoid (anterior, medial, and posterior fibres), and pectoralis major (clavicular fibres) (Muceli et al. 2010; Gentner et al. 2013; Steele et al. 2013; Roh et al. 2015). EMG electrodes were placed in accordance with the European recommendations for surface electromyography (Hermens et al. 1999), and the signals were amplified and band-pass filtered (20–450 Hz) (Roh et al. 2013, 2015). Each muscle's EMG signal was normalized to the maximum observed value of the signal. The preprocessed EMG data were then stored in two sets, the dominant and nondominant limb, each including data from eight muscles.

To calculate joint angles (i.e., motion effectors) from marker positions, a human upper body musculoskeletal model developed by Holzbaur (2005) for the OpenSim environment (Delp et al. 2007) was used. OpenSim is an open source musculoskeletal simulation platform that provides a variety of human models and motion and motion generation simulation algorithms (simtk.org/home/opensim). The original model only includes the right extremity. This model was modified and expanded to include both extremities and to be compatible with Kinect data. With the use of OpenSim software and the modified musculoskeletal model, the inverse kinematics of the marker motions were solved to find the joint angles.

Solving the inverse kinematics problem provides the change in the following joint angles over time: trunk motion as measured by roll, pitch, and yaw angles, flexion-extension of both shoulders, abduction-adduction of both shoulders, mediolateral rotation of both shoulders, flexion-extension of both elbows, pronation-supination of both elbows, radial-ulnar deviation of both wrists, and flexion-extension of both wrists (17 DOFs). With the use of this procedure, the joint angle time series during a motor exploration task for all 15 participants was calculated at 30 Hz. These data were then bifurcated with each set containing the joint angle time series data of the dominant and nondominant upper limbs of each participant (10 DOFs in each set; trunk motion data was shared). Only movements within 2 SD of the mean speed of the entire session were kept for further analysis. This was to ensure that all periods of pause or no movement were filtered out. The joint motion data were low-pass filtered at 6 Hz (Enoka 2015; Valdés et al. 2015). Synergy analysis of kinematics and EMG data was performed independently for the dominant and nondominant limb data sets (i.e., within-arm synergies, not between-arm synergies).

Quantifying synergies by linear decomposition of data.

Following the common formulation in the literature (Cheung et al. 2009; Bizzi and Cheung 2013; Berger and d'Avella 2014; Roh et al. 2015), a t × m matrix M containing the time-series of change in m motion effectors (muscle EMGs or joint angles) during a functional task can be measured (t is the number of data points). A factorization method (one of PCA, NNMF, and ICA in this study) will solve for a set of n synergy vectors w (1 × m dimensional) arranged in an n × m synergy structure matrix W (n < m). Each synergy vector specifies a relative mode of activation/use of the motion effectors during the task. This synergy structure is found so that the error in reconstructing the motion elements in matrix M using a linear combination of the synergy vectors is minimized. This linear combination of the synergy vectors is expressed as M = C × W + E, where C is a t × n activation matrix and E is the unexplained variation.

Although the three factorization methods considered in this study assume that the data can be reconstructed using a linear combination of a set of basis vectors (M = C × W + E), they employ different assumptions and algorithms to find such basis vectors. More specifically, PCA uses singular value decomposition (SVD) to find basis vectors that best describe the variance (objective function) of the data while minimizing the covariance of the basis vectors (constraint). This can be solved analytically using SVD, which returns the eigenvectors of the covariance matrix of the data as the PCA basis vectors. This means that the largest part of the variability (mean) in the data can be reconstructed along the first basis vector (the eigenvector with the highest eigenvalue). The next vectors describe the directions that contain the highest deviation from the mean value. PCA vectors are orthogonal (eigenvectors are orthogonal) and therefore independent. As PCA utilizes second-order statistics (variance and covariance), it works best on Gaussian data sets with minimal noise and nonlinearity.

Like PCA, NNMF also utilizes second-order statistics and finds vectors that best describe the variance of the data (objective function). NNMF constrains both C and W matrices to be nonnegative and iteratively improves a set of initial guess vectors. Nonnegativity of C and W matrices makes the optimization problem convex, ensuring that the outcomes are true global minima and not a local minimum. In a nonnegative space, the basis vectors cannot be orthogonal. Nevertheless, the basis vectors are required to be independent.

ICA was developed to deal with non-Gaussianity in data and therefore utilizes higher moments of the data. ICA finds basis vectors that maximize the absolute value of the fourth moment “kurtosis” of the data. Kurtosis is a measure of tailedness of the probability distribution of a real-valued random variable (indicating non-Gaussianity of data). This will generate basis vectors that are statistically independent. ICA works particularly well to separate a multivariate signal (1 sensor recording multiple sources at the same time) into independent non-Gaussian signals (source signals), an example of which is the cocktail party problem: a partygoer hears the sum of voices of people (sources) chatting at a party but can decompose the aggregate incoming signal into what each person is saying.

Analysis of factorization performance using healthy motion data.

The collected data were divided to muscle and kinematic sets, each set containing separate time series data for the dominant and nondominant hands. After preprocessing the data, a k-fold cross validation (k = 20) was implemented to compare the performance of the factorization algorithms. Within each fold, data were divided into 5-s epochs. Within each epoch, 80% of the data was randomly assigned to the training set and the remaining 20% was assigned to the validation set of that fold. Within each fold, the validation data set was used to assess the performance of the dimensionality reduction methods on the training data set.

Variance accounted for (VAF) was used to determine the number of synergy vectors ensuring factorization methods sufficiently learned the training data (Tresch et al. 2006). The number of synergy vectors is the minimum number of synergies that achieves a global (across all training data points) VAF >90%, with a <5% increase in global VAF upon addition of another synergy vector. As a local criterion, the VAF for each muscle or joint (DOF VAF) is required to exceed 50%. This procedure ensures that the estimated number of synergies could predict both the overall data set as well as each of the DOFs of the overall data set (Ting and Chvatal 2010; Roh et al. 2013, 2015). We started this study by considering four factorization methods, PCA, NNMF, ICA, and factor analysis (Tresch et al. 2006). Factor analysis did not fulfill the training requirements and therefore was eliminated from the study.

Once the synergy structure of a fold of training data was identified, six metrics were used to quantify the performance of the factorization methods: number of identified synergies, average reconstruction error of both training and validation data sets, average correlation coefficient between the original data and the reconstructed data for both training and validation data sets, and dimension of the common subspace between the training and validation data sets (number of synergy vectors of the 2 data sets that have a strong correlation r > 0.9). To determine the first four metrics, the synergy structure of the training data was used to reconstruct both training and validation data sets. The six goodness of fit metrics considered in this study can be divided into three categories: category 1: two metrics to study the structure of the data (synergy vectors); category 2: two metrics to quantify how well-identified synergies can be used to reconstruct the data (reconstruction error); and category 3: two metrics to observe correlation of the original and reconstructed data sets.

The average performance of the factorization methods over the k-fold for each participant was used to statistically compare the methods. Finally, a two-way ANOVA was conducted to quantify the effect of different factorization methods [3 levels each at n = 2 (number of limbs) × 15 (number of participants) = 30: PCA, NNMF, ICA] and hand dominance [2 levels each at n = 3 (number of factorization methods) × 15 (number of participants) = 45: dominant vs. nondominant limb] on factorization performance. This model is valid if the interaction between choice of factorization method and hand dominance is statistically nonsignificant. MATLAB R2014b on a high-end desktop computer running Windows 7 was used for this study.

Comparison of identified synergy vectors using simulated data.

We created three sets of randomly generated, 2D data sets (3 M matrices of size 500 × 2, containing simulated muscle activations m₁ and m₂) to demonstrate the differences in how PCA, NNMF, and ICA identify synergy vectors to decompose variability in data. Two vectors w₁ = (0.25, 1) and w₂ = (1, 0.25) were used as the original basis vectors (synergies) to create the three data sets. The first set was created by randomly assigning the activation signals c₁ and c₂ from a uniform distribution between 0 and 1 (unimodal data with equal importance between the two basis vectors). The second set was created by randomly assigning the activation signals c₁ from a uniform distribution between 0 and 0.3, and c₂ from a uniform distribution between 0 and 1 (unimodal data favoring w₂). Finally, the third set was created by combining two unimodal data sets, one favoring w₁ and one favoring w₂, to create a bimodal data set. We then applied PCA, NNMF, and ICA to each of data sets to compare the synergy structure identified by each method.

RESULTS

Variation in the data (behavior, joint kinematics, EMG) during the task.

Each of the participants completed a 5-min data collection session. During the data collection session, participants played Lucky Pirate by moving their hands to move a cursor on the screen to different treasure chests. Participants were able to set their own pace and open as many chests as they wanted as long as they continuously moved their hands and played the game without any extended pauses.

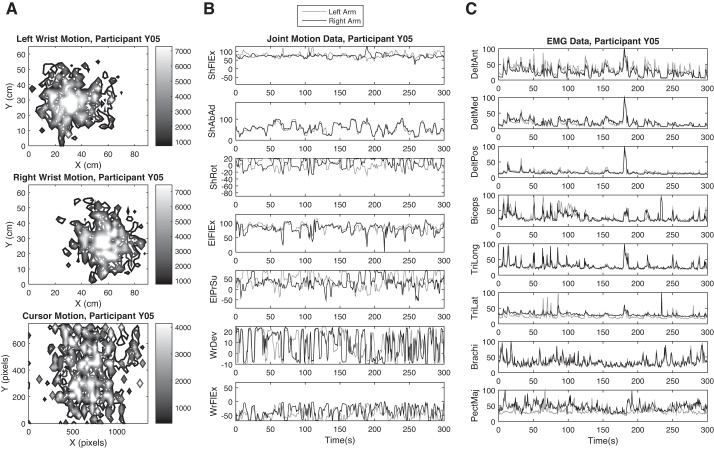
Figure 2 shows the collected data from participant Y05 (male, right handed, 29 yr old) as an example. Figure 2A shows the distribution of the wrists' position (top and middle, task space motion). The wrists' position were translated by the FEATHERS software into the motion of the cursor on the computer screen (Fig. 2A, bottom). The contours in Fig. 2A are color coded to show the minimum observed time spent at each point in a workspace in the frontal plane (the points that are surrounded by a contour line have appeared in the position data for at least the amount of time that corresponds with the color of the contour line in ms). The origin of the workspace in the Fig. 2, top and middle, was set to the lowest leftmost point that the participant's left hand visited during game play.

Fig. 2.

Variation in the data (behavior, joint kinematics, EMG) during the task for participant Y05. A: contour plots showing the time distribution of position of the wrists and the computer cursor. B: joint motion data in degrees. Joint names: ShFlEx, ShAbAd, and ShRot, shoulder flexion/extension, abduction/adduction, and rotation; ElFlEx and ElPrSu, elbow flexion/extension and pronation/supination; WrDev and WrFlEx, wrist ulnar deviation and flexion/extension. C: normalized EMG data. Muscle names: DelAnt, DelMed, and DelPos are anterior, medial, and posterior fibers of deltoid; biceps, biceps brachii; TriLong and TriLat, long and lateral heads of triceps; brachi, brachioradialis; PectMaj, clavicular fibers of pectorialis major.

Figure 2, B and C, shows the recorded joint motion (degrees) and EMG (normalized to maximum observed in the channel) data from participant Y05. All the joints and muscles considered in this study were active and involved during the task. However, their activity did not follow any specific pattern. Moreover, the recorded activity of some joints and muscles (e.g., shoulder abduction/adduction, elbow flexion/extension, deltoid posterior, and brachiradialis) was very similar between the two arms. These joints and muscles are mainly involved in up and down motions of the hands, which were symmetric as the participant completed the task. For other joints and muscles, the recorded activities from the left and right arm were asynchronous and dissimilar as they control right-left motions of the hands, which were not symmetric during the task. For example, to move the hands rightward, the right arm extends away from the body and the left arm flexes toward the midpoint of the body, causing asymmetry in the motion of joints and activation of muscles between the two arms.

Comparison of synergy structures identified by each method using simulated data.

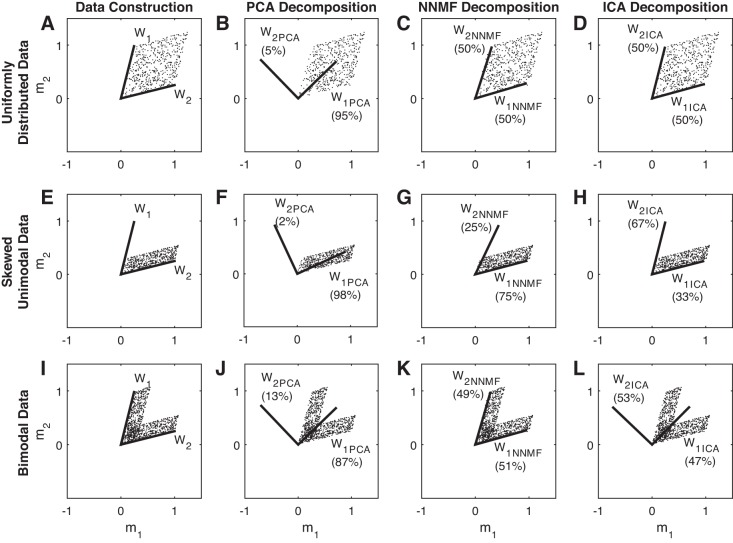
We used three sets of simulated 2D data sets (scattered dots on each row of Fig. 3) to demonstrate the differences in how PCA, NNMF, and ICA identify basis vectors to decompose variability in data. Two vectors w₁ = (0.25, 1) and w₂ = (1, 0.25) were used as the original basis vectors (synergies) to create all three data sets (muscle activations m₁ and m₂). These two vectors are shown on Fig. 3, A, E, and I, with solid lines. The three data sets created were as follows: 1) unimodal data with equal importance between the two basis vectors, Fig. 3, A–D; 2) unimodal data favoring variance along w₂, Fig. 3, E–H; and 3) bimodal data, Fig. 3, I–L; see methods for more details. The solid lines in Fig. 3, B, F, and J demonstrate the basis vectors identified by PCA; NNMF basis vectors are illustrated in Fig. 3, C, G, and K; and ICA basis vectors are illustrated in Fig. 3, D, H, and L. The numbers by each of the basis vectors indicate what percentage of the variance in the data can be reconstructed using that vector.

Fig. 3.

A 2-dimensional example illustrating differences between synergy structures identified using principal component analysis (PCA), nonnegative matrix factorization (NNMF), and independent component analysis (ICA) on 3 different data types. A–D: uniformly distributed data. E–H: skewed unimodal data. I–L: bimodal data.

Neither of the PCA basis vectors are similar to the original basis vectors. The first PCA basis vector aligns with the “center” of the data and explains most of the variance in the data, and the second vector is always orthogonal to the first vector. Moreover, NNMF basis vectors consistently identify the edges of the data set. Finally, ICA returns basis vectors that are similar to NNMF basis vectors on unimodal data but returns basis vectors that are similar to those of PCA on bimodal data.

Goodness of fit comparison: kinematic synergies.

Following the analysis procedures explained in methods, a k-fold cross validation with 20-fold was implemented to study how well different factorization methods can reduce the kinematic dimensionality of exploratory reaching movements of the dominant and nondominant sides of the body. For each side of the body 10 DOFs were included in this analysis (3 at trunk, 3 at shoulder, 2 at elbow, and 2 at wrist). For each participant's dominant and nondominant side, using the created 20-fold of training and validation data sets, we quantified the kinematic synergy structure by applying PCA, NNMF, and ICA. Then, the performance of each factorization method was determined using the introduced goodness of fit metrics: 6 performance metrics (average of the 20-fold), on each of the 2 sides of the body, for each of the 15 participants, for each of the 3 methods. We used this data in a two-way ANOVA to quantify the effect of different factorization methods (3 levels each at n = 30: PCA, NNMF, ICA) and hand dominance (2 levels each at n = 45: dominant vs. nondominant limb) on factorization performance. The interaction between choice of factorization method and hand dominance was statistically nonsignificant. Table 1 shows a summary of all the performance metrics and how they vary between the two limbs for each factorization method.

Table 1.

Kinematic synergies: comparison of different goodness of fit metrics between the two sides of the body for each factorization method

	PCA	NNMF	ICA
No. of identified synergies
Dominant limb	3.4 ± 0.7	4.1 ± 1.1	2.8 ± 0.6
Nondominant limb	3.7 ± 0.6	4.3 ± 1.1	2.9 ± 0.7
Both limbs	3.5 ± 0.7	4.2 ± 1.1	2.8 ± 0.7
Average reconstruction error (training data), °
Dominant limb	8.7 ± 1.5	9.8 ± 1.4	13.4 ± 1.3
Nondominant limb	7.8 ± 1.3	9.7 ± 1.2	13.8 ± 1.8
Both limbs	8.2 ± 1.5	9.8 ± 1.3	13.6 ± 1.6
Average reconstruction error (validation data), °
Dominant limb	8.8 ± 1.6	7.8 ± 1.9	10.8 ± 1.5
Nondominant limb	7.9 ± 1.3	7.3 ± 1.8	10.7 ± 1.9
Both limbs	8.3 ± 1.5	7.6 ± 1.8	10.8 ± 1.7
Correlation coefficient of training data
Dominant limb	0.96 ± 0.01	0.98 ± 0.02	0.95 ± 0.01
Nondominant limb	0.96 ± 0.01	0.97 ± 0.01	0.95 ± 0.01
Both limbs	0.96 ± 0.01	0.97 ± 0.02	0.95 ± 0.01
Correlation coefficient of validation data
Dominant limb	0.96 ± 0.01	0.97 ± 0.02	0.97 ± 0.01
Nondominant limb	0.96 ± 0.01	0.97 ± 0.02	0.97 ± 0.01
Both limbs	0.96 ± 0.01	0.97 ± 0.02	0.97 ± 0.01
Common synergies (training and validation data), %
Dominant arm	95 ± 6	96 ± 5	70 ± 17
Nondominant arm	97 ± 4	95 ± 5	78 ± 18
Both limbs	96 ± 5	95 ± 5	73 ± 18
Training time, s	4 ± 0.2	15 ± 6	13 ± 3

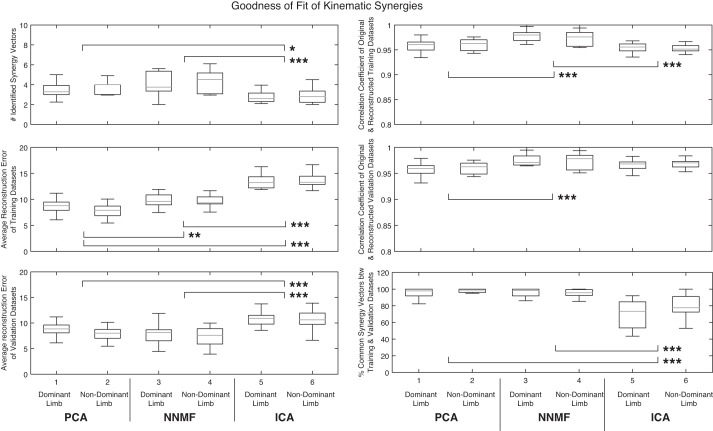
The number of synergy vectors that satisfied the training criteria differed between the dominant and nondominant limbs. On average, more synergy vectors were required to capture the variance in the motion data from the nondominant limb across all factorization methods, although this difference was not statistically significant (P = 0.32). On the other hand, choice of factorization method had a statistically significant effect on the number of identified synergies. ICA required a lower number of synergy vectors to summarize the variance in the data compared with PCA (2.8 vs. 3.5 synergy vectors, P < 0.01) and NNMF (2.8 vs. 4.2 synergy vectors, P < 0.001). The difference between PCA and NNMF was not statistically significant. Figure 4 shows the effects and statistical significance of choice of factorization method as well as dominance of the limb on the performance metrics.

Fig. 4.

Kinematic synergies' goodness of fit: effects and statistical significance of choice of factorization method and limb dominance on the performance metrics. Measures showing a significant difference between the factorization methods are indicated: *P <0.05, **P <0.01, and ***P <0.001.

Dominance of the limb did not have any significant effect on the average reconstruction error (reconstruction of the nondominant limb's data returned a slightly lower reconstruction error, P = 0.67 for the training data set and P = 0.21 for the validation data set). However, choice of factorization method had a statistically significant effect on this performance metric. In reconstructing the training data sets from synergy vectors of the training data, PCA had the lowest reconstruction error compared with both NNMF (8.2 vs. 9.8°, P < 0.01) and ICA (8.2 vs. 13.6°, P < 0.001). In this case, the difference between NNMF and ICA was also significant (9.8 vs. 13.6°, P < 0.01). The same relationship was observed in reconstructing the validation data sets from synergy vectors of the training data. ICA had a significantly larger reconstruction error compared with PCA (10.7 vs. 8.3°, P < 0.001) and NNMF (10.7 vs. 7.6°, P < 0.001). However, the difference between PCA and NNMF's ability to reconstruct the validation data was not significant.

The effect of dominance of the limb was not significant on the correlation coefficient of the original and reconstructed data (P = 0.89 for training and P = 0.49 for validation data set). However, the choice of factorization method had a statistically significant role in determining this performance metric. On training data sets, NNMF-based reconstructed training data had a larger correlation coefficient with the original training data compared with PCA (0.97 vs. 0.96, P < 0.001) and ICA (0.97 vs. 0.95, P < 0.001). Moreover, NNMF-based reconstructed validation data had a larger correlation coefficient with the original validation data compared with PCA (0.97 vs. 0.96, P < 0.01).

Similar to the other performance metrics, dominance of the limb did not have a statistically significant effect on the percentage of common synergy vectors between training and validation data (P = 0.24), whereas the effect of choice of factorization method was significant. Although the difference between PCA and NNMF was not significant on this metric, they both returned a significantly higher percentage of common synergies between training and validation data compared with ICA (PCA and NNMF vs. ICA: 96 and 95 vs. 73%, both at P < 0.001).

We also considered each method's training time (i.e., time spent to factorize the 20-fold of data for each participant) as a measure of computational efficiency of the methods. PCA returned the synergy structure significantly faster than NNMF (4 vs. 15 s, P < 0.001) and ICA (4 vs. 13 s, P < 0.001).

Goodness of fit comparison: muscle synergies.

Following the analysis procedures explained in methods, a k-fold cross validation with 20-fold was implemented to study how well different factorization methods can reduce the dimensionality observed in the participants' EMG data during exploratory reaching. For each side of the body, EMGs of eight muscles were included in this analysis. For each participant's dominant side and nondominant side, using the 20-fold of training and validation data sets, we quantified the muscle synergy structure by applying PCA, NNMF, and ICA. Performance of each factorization method was determined using the same goodness of fit metrics as for the kinematic data: 6 performance metrics (average of the 20-fold), on each of the 2 sides of the body, for each of the 15 participants, for each of the 3 methods. We used these data in a two-way ANOVA to quantify the effect of different factorization methods (3 levels each at n = 30: PCA, NNMF, ICA) and hand dominance (2 levels each at n = 45: dominant vs. nondominant limb) on factorization performance. The interaction between choice of factorization method and hand dominance was statistically nonsignificant. Table 2 shows a summary of all the performance metrics and how they vary between the two limbs for each factorization method.

Table 2.

Muscle synergies: comparison of different goodness of fit metrics between the two sides of the body for each factorization method

	PCA	NNMF	ICA
No. of identified synergies
Dominant limb	3.2 ± 0.9	3.5 ± 1.3	5.4 ± 1.1
Nondominant limb	3.5 ± 0.9	3.7 ± 1.0	5.5 ± 1.2
Both limbs	3.4 ± 0.9	3.6 ± 1.1	5.4 ± 1.1
Average reconstruction error (training data), %
Dominant limb	3.0 ± 0.9	2.9 ± 1.0	2.7 ± 1.0
Nondominant limb	2.8 ± 0.8	2.7 ± 0.9	2.4 ± 1.1
Both limbs	2.9 ± 0.8	2.8 ± 0.9	2.5 ± 1.0
Average reconstruction error (validation data), %
Dominant limb	3.0 ± 0.9	2.9 ± 1.0	2.0 ± 1.0
Nondominant limb	2.8 ± 0.8	2.7 ± 0.9	1.9 ± 1.0
Both limbs	2.9 ± 0.8	2.8 ± 0.9	2.0 ± 1.0
Correlation coefficient of training data
Dominant limb	0.89 ± 0.03	0.90 ± 0.02	0.89 ± 0.01
Nondominant limb	0.88 ± 0.05	0.90 ± 0.01	0.89 ± 0.01
Both limbs	0.89 ± 0.04	0.90 ± 0.02	0.89 ± 0.01
Correlation coefficient of validation data
Dominant limb	0.89 ± 0.03	0.90 ± 0.03	0.92 ± 0.04
Nondominant limb	0.89 ± 0.04	0.90 ± 0.02	0.92 ± 0.04
Both limbs	0.89 ± 0.04	0.90 ± 0.02	0.92 ± 0.04
Common synergies (training and validation data), %
Dominant limb	94 ± 6	95 ± 5	50 ± 9
Nondominant limb	94 ± 7	95 ± 6	58 ± 11
Both limbs	94 ± 6	95 ± 5	54 ± 11
Training time, s	5 ± 1	33 ± 17	40 ± 20

On average, more synergy vectors were required to capture the variance in the data from the nondominant limb, across all factorization methods. However, this difference was not statistically significant (P = 0.39). On the other hand, choice of factorization method had a statistically significant effect on the number of identified synergies. ICA required a higher number of synergy vectors to summarize the variance in the data compared with PCA (5.4 vs. 3.4 synergy vectors, P < 0.001) and NNMF (5.4 vs. 3.6 synergy vectors, P < 0.001). The difference between PCA and NNMF was not statistically significant. Figure 5 shows the effects and statistical significance of choice of factorization method as well as dominance of the limb on the performance metrics.

Fig. 5.

Muscle synergies' goodness of fit: effects and statistical significance of choice of factorization method and limb dominance on the performance metrics. Measures showing a significant difference between the factorization methods are indicated: *P <0.05, **P <0.01, and ***P <0.001.

Reconstruction of the nondominant limb's data returned a slightly lower error; however, this difference was not statistically significant (P = 0.36 for training and P = 0.43 for validation data sets). On the other hand, choice of factorization method had a statistically significant effect on this performance metric. The three methods did not show any statistically significant differences in reconstructing the training data sets from the identified synergy vectors. However, ICA had significantly lower reconstruction error compared with PCA (2.0 vs. 2.9%, P < 0.01) and NNMF (2.0 vs. 2.8%, P < 0.01) in reconstructing the validation data sets. The difference between PCA and NNMF in their ability to reconstruct the validation data was not significant.

The effect of dominance of the limb was not significant on the correlation coefficient of the original and reconstructed data (P = 0.62 for both training and validation sets). However, the choice of factorization method was statistically significant (validation set only). ICA-based reconstructed validation data had a larger correlation coefficient with the original validation data compared with PCA (0.92 vs. 0.89, P < 0.01) and NNMF (0.92 vs. 0.90, P < 0.05).

Similar to the other performance metrics, dominance of the limb did not have a statistically significant effect on the percentage of common synergy vectors between training and validation data (P = 0.14), whereas the effect of choice of factorization method was significant. Although the difference between PCA and NNMF was not significant on this metric, they both returned a significantly higher percentage of common synergies between training and validation data compared with ICA (PCA and NNMF vs. ICA: 94 and 95 vs. 54%, both at P < 0.001).

Considering each method's training time (i.e., time spent to factorize the 20-fold of data for each participant) as a measure of computational efficiency, PCA significantly outperformed NNMF (5 vs. 33 s, P < 0.001) and ICA (5 vs. 40 s, P < 0.001).

DISCUSSION

Factorization performance.

Considering the kinematic synergies, hand dominance had no significant effect on the factorization performance. On average, ICA identified the lowest number of synergy vectors, followed by PCA and NNMF. Despite the compactness of ICA's factorization, this method had the statistically significant largest reconstruction error. The difference between PCA and NNMF's reconstruction errors was also statistically significant. All three algorithms returned a strong correlation coefficient between the original data and the reconstructed data for both training and validation data sets (r > 0.95). ICA had the statistically significant lowest dimension of common subspace between the training and validation data sets compared with PCA and NNMF. ICA had the worst factorization performance compared with PCA and NNMF. Although PCA and NNMF had comparable performance on goodness of fit measures, PCA had a statistically significant lower training time (4 s) compared with NNMF (13 s).

Specifically considering the muscle synergies, hand dominance had no significant effect on the factorization performance. On average, PCA factorized the data with the lowest number of synergy vectors, followed by NNMF and ICA. There was no statistically significant difference between the three algorithms on reconstruction error of training and validation data sets. Similarly, there was no statistically significant difference between the three algorithms on correlation coefficient between the original training data and the reconstructed training data. ICA had a statistically significant better correlation coefficient between the original and the reconstructed validation data set compared with PCA and NNMF. However, PCA and NNMF significantly outperformed ICA in returning a higher value for the dimension of common subspace between the training and validation data sets (93.8, 95.2, and 54.0% for PCA, NNMF, and ICA. No statistical difference between PCA and NNMF). This means that ICA failed to identify the same synergy structure between the training and validation data sets, making it an unreliable factorization method. As with joint motion results, PCA had a statistically significant lower training time (5 s) compared with NNMF (33 s) and ICA (40 s) on the EMG data.

To compare our results with similar studies, consider Tresch et al. (2006) and Steele et al. (2015), who empirically compared performance of six matrix factorization methods on simulated and animal EMG data: NNMF, PCA, factor analysis, and different ICA algorithms. Although factor analysis showed a relatively high performance in Tresch et al. (2006), it could not pass the training requirement of producing a factorization with a minimum VAF for each muscle or joint (DOF VAF) of 50%. This local criterion ensures that the identified synergies can predict both the overall data set as well as each of the DOFs of the overall data set. However, it was not included in Tresch et al. (2006) as a training requirement. Our reported performance of PCA, NNMF, and ICA on kinematic and EMG data from healthy participants is comparable to the performance of these methods as reported in Tresch et al. (2006) and Steele et al. (2015) on simulated and animal EMG data.

Goodness of fit comparisons.

The six goodness of fit metrics considered in this study can be divided into three categories: category 1: two metrics concerned the structure of the data (synergy vectors); category 2: two metrics concerned how well-identified synergies can be used to reconstruct the data (reconstruction error); and category 3: two metrics concerned correlation of the original and reconstructed data sets. Of the two metrics of structure (category 1), “number of identified synergy vectors” provides an estimate of how well the factorization method can condense the data. From a numerical point of view this is an important measure when the data size is big. However, in this study the focus is on functional synergies and interpretation of three vs. four synergy vectors does not add any additional challenge. On the other hand, “percentage of common synergy vectors between training and validation data sets” provides a much richer estimate of how well a factorization method can identify the underlying structure of the data (coordination of joints or muscles in this study).

It is beneficial to reflect on the meaning of statistical significance and whether statistical significance can be interpreted as a tangible difference. Accordingly, the statistically significant differences observed between the values of the category 3 metrics across the factorization methods need to be interpreted cautiously. Although statistical significance was observed, all three of the factorization methods produced reconstructed data sets that strongly correlated with the original data sets (strong correlation is considered r > 0.7, compared with the worst case of r > 0.89 for PCA on EMG data). This makes the correlation coefficient metric a weak candidate for quantifying goodness of fit of the considered factorization methods.

Differences between the mathematical principles of the factorization models.

Understanding the mathematical principles that are used in matrix factorization methods (see methods for an overview) can assist in explaining the inferior performance of ICA compared with PCA and NNMF. Going back to Fig. 3, we see that neither of the PCA basis vectors look like the original basis vectors used to create the data sets. The first PCA basis vector aligns with the “center” of the data and explains most of the variance in the data (87–98%) depending on how wide/divergent from the center (Fig. 3, B and J) or thin (Fig. 3F) the data set is. The second PCA vector is orthogonal to the first one and explains a much lower variance in the data. The VAF of the second vector can be considered a measure of scatteredness. PCA basis vectors, resembling performance of a multiple regression line, capture the mean and (residual) variance from the mean. This means some data points might have a negative activation c along the second basis vector, making interpretation of activation matrix C in functional tasks hard (e.g., a muscle can be negatively activated).

NNMF identifies vectors that describe a subspace within which all data points will lie. The nonnegativity constraint dictates that only the points between the identified vectors can be reconstructed. Therefore, NNMF basis vectors identify the edges of the data set. This means that the importance of the original basis vectors and uni/bimodality of the data do not play a role in identifying the basis vectors, whereas PCA basis vectors change based on the importance of the original basis vectors as this changes the major direction of the data (i.e., mean). NNMF's nonnegativity condition for activation of basis vectors is a useful attribute in identifying physiologically meaningful synergies as it prevents outputs containing negative activation of the muscles. In sum, researchers utilizing motor synergies need to be cognizant of the differences in the nature of the basis vectors returned by PCA and NNMF and interpret them accordingly. Specifically, one cannot compare the synergy structures of a PCA-based and an NNMF-based study.

Considering the results presented in Fig. 3, ICA performs well on unimodal data sets, and similar to NNMF, it can identify the original basis vectors that define the edges of the data. However, NNMF can identify the importance of the vectors better than ICA can. Data in Fig. 3, E–H, black dots, were created by randomly assigning the activation signals c₁ from a uniform distribution between 0 and 0.3 and c₂ from a uniform distribution between 0 and 1 (unimodal data favoring w₂ over w₁ with a 3.3 to 1 ratio). The VAF ratio between NNMF basis vectors is 75 to 25%, closer to the weighting of the original basis vectors, compared with ICA of 67 to 33%. Moreover, on the bimodal data set, ICA identifies basis vectors that are similar to those found by PCA, describing mean and variance from the mean. This shift from describing the edge of the data to the major direction of the data can cause confusion in interpreting the results of the decomposition if the nature of the data is unknown.

It is worthwhile to repeat that ICA was developed for decomposition of non-Gaussian data, specifically data with a flat distribution curve (as opposed to a bell curve). On the other hand, PCA and NNMF use second-order statistics (mean and variance, both Gaussian features) to decompose data. Joint motion and EMG data have a low level of non-Gaussianity and have a skewed bell curve distribution [a portion of the elbow extension-flexion range of motion (ROM) is used to do a specific task and moving away from that zone of the ROM makes completion of the task hard, thus reducing the chances of the elbow being moved to those zones]. Naturally, on the relatively Gaussian joint motion and EMG data presented in this study, PCA and NNMF outperform ICA. Also, PCA is a faster method as it returns an analytic solution whereas NNMF and ICA numerically and through iterations find the basis vectors. However, NNMF can identify nonnegative synergy vectors and activation signals, making interpretation of the synergy structure easier and physiologically more meaningful and, ultimately, making NNMF a preferable method to PCA.

Interpretation of the synergy vectors: example from one participant.

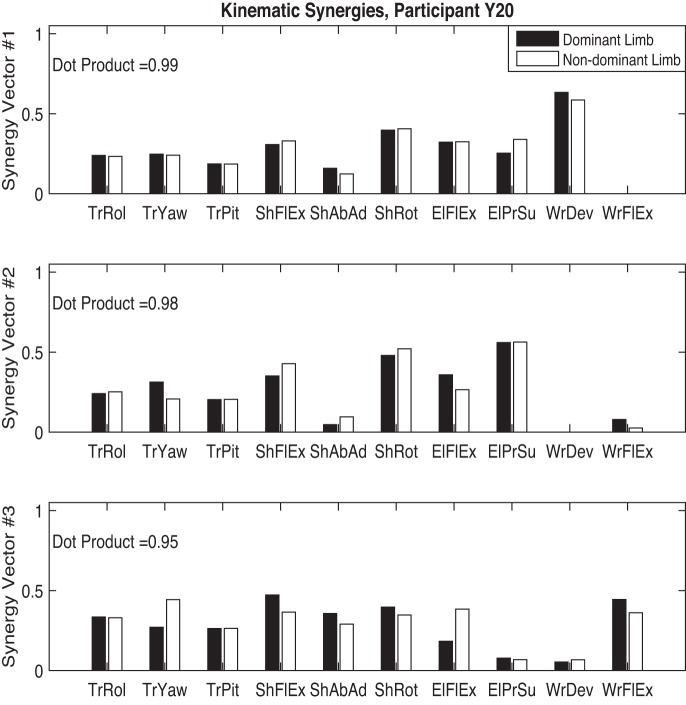
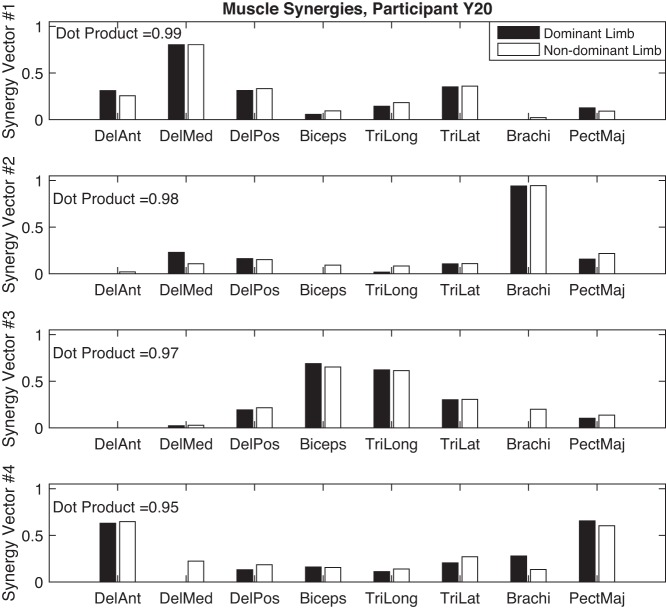
To further discuss interpretation of synergy vectors, we used NNMF to extract kinematic and muscle synergies from motion data of participant Y20 (female, right handed, 27 yr old). Figures 6 and 7 show the kinematic and muscle synergy vectors for both dominant and nondominant limbs of this participant, extracted with the training criteria introduced previously. Within kinematic and EMG data sets, synergy vectors of the two limbs were matched based on their similarity as measured by the dot product of the synergy vectors of the two limbs. Interestingly, the synergy structure of the dominant and nondominant limbs are similar for this participant [to consider 2 vectors similar, their dot product must be >0.8 (Roh et al. 2012)]. The bimanual task required similar motions in the task space [i.e., moving the 2 hands toward the same without requiring the participant to match the motion generation (EMG) and the joint space variations between the 2 limbs]. However, as shown by the similarity of the synergy vectors, the modules controlled by the CNS to create the nonsynchronized (both spatial and temporal) motions of the two limbs in the task space are similar. This suggests that the CNS uses the same control strategy to coordinate the motion of the two limbs. However, confirming this requires further studies to investigate whether within limb synergies are similar across all participants. Naturally, this leads to another question, whether or not healthy adults utilize the same synergy set to generate reaching motions (between subjects similarities). We plan to address these questions in our future work.

Fig. 6.

Kinematic synergies of the dominant and nondominant limbs of participant Y20. TrRol, trunk roll; TrYaw, trunk yaw; TrPit, trunk pitch; ShFlEx, shoulder flexion-extension; ShAbAd, shoulder abduction-adduction; ShRot, mediolateral shoulder rotation; ElFlEx, elbow flexion-extension; ElPrSu, elbow pronation-supination; WrDev, wrist radial-ulnar deviation; WrFlEx, wrist flexion-extension.

Fig. 7.

Muscle synergies of the dominant and nondominant limbs of participant Y20. DelAnt, deltoid anterior; DelMed, deltoid medial; DelPos, deltoid posterior; Biceps, biceps brachii; TriLong, triceps brachii long heads; TriLat, triceps brachii lateral heads; Brachi, brachioradialis; PectMaj, pectorialis major (clavicular fibers).

The three synergy vectors presented in Fig. 6 sufficed to return a VAF value over 98% for the kinematic data. Each synergy vector shows how different DOFs (joints or muscles) are activated relative to the other DOFs. Motion of the trunk as measured by roll, pitch, and yaw angles is represented by a similar relative activation in all three kinematic synergies. This consistency across synergies suggests that the trunk motion is not a module in controlling the reaching motions (lack of compensatory motions in trunk). On the opposite side, the involvement of the wrist DOF is very modular: synergy 1 only activates wrist deviation while synergy 3 is responsible for activation of wrist flexion-extension. Motion of the shoulder and elbow joints is represented in all three synergies, suggesting a more complex coordination strategy compared with the wrist joint.

Figure 7 shows the four muscle synergies that fulfilled the training criteria. Synergy 1 involves the activation of deltoid muscles and triceps brachii (lateral head) which can generate shoulder abduction and flexion. Synergy 2 activates brachioradialis which can generate fast flexion at the elbow and can stabilize the motion of wrist during extension and radial deviation. Vector 3 shows the synergistic activation of biceps brachii and triceps brachii (long and lateral heads) during elbow flexion and extension. Finally, synergy 4 activates anterior fibers of deltoid and pectorialis major simultaneously, generating flexion, and rotation in shoulders.

Summary.

Having an understanding of the factorization algorithms, researchers can choose the most robust algorithm to characterize the synergies observed during a functional task performed by healthy participants. This will define a “healthy” profile of motor synergies employed during arm motions. These healthy synergies can be used to study how neural injuries, for example, stroke, can change motor synergies. This knowledge can be used in quantifying motor deficits, fulfilling the need for more objective clinical assessments (Lam et al. 2015; Tatla et al. 2015) and informing the design of individualized care for physical therapy clients. Moreover, as suggested by Safavynia et al. (2011) and Urra et al. (2014), motor synergies can be used as performance metrics in developing effective new therapy tools that increase engagement of therapy clients in their exercise (similar to our previous works; Shirzad and Van der Loos 2012, 2013, 2016).

Conclusion.

Systematic comparisons of factorization methods for motor synergy identification were previously done using numerically generated and experimental data from frogs (Tresch et al. 2006) and simulated data from a musculoskeletal model (Steele et al. 2015). This paper presented a comparison of three factorization methods on identifying kinematic and muscle synergies in human data. PCA and NNMF had a comparable performance on both EMG and joint motion data and both outperformed ICA. However, NNMF's nonnegativity condition for activation of basis vectors is a useful attribute in identifying physiologically meaningful synergies, making it a more appealing method for future studies. Through a simple 2D example, we demonstrated the nature of the synergy vectors identified by each of the three methods, highlighting that PCA vectors describe the major direction of the data (means ± SD) and NNMF vectors describe the edges of the data. This difference needs to be considered in interpreting the functional meaning of the synergy vectors. The results presented here can be used to unify the methods in motor synergy research, building a common ground for understanding “healthy” motor coordination. This knowledge can lead to an understanding of the effects of different motor deficits on motor synergies and the nature of motor recovery and, ultimately, creating individualized care for physical therapy clients.

GRANTS

This research is supported by the University of British Columbia (UBC) and the Natural Sciences and Engineering Research Council (NSERC) of Canada.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

N.L.-S. performed experiments; N.L.-S. analyzed data; N.L.-S. interpreted results of experiments; N.L.-S. prepared figures; N.L.-S. drafted manuscript; N.L.-S. and H.F.M.V.d.L. edited and revised manuscript; N.L.-S. and H.F.M.V.d.L. approved final version of manuscript.