DNA Occupancy of Polymerizing Transcription Factors: A Chemical Model of the ETS Family Factor Yan

Abstract

Transcription factors use both protein-DNA and protein-protein interactions to assemble appropriate complexes to regulate gene expression. Although most transcription factors operate as monomers or dimers, a few, including the E26 transformation-specific family repressors Drosophila melanogaster Yan and its human homolog TEL/ETV6, can polymerize. Although polymerization is required for both the normal and oncogenic function of Yan and TEL/ETV6, the mechanisms by which it influences the recruitment, organization, and stability of transcriptional complexes remain poorly understood. Further, a quantitative description of the DNA occupancy of a polymerizing transcription factor is lacking, and such a description would have broader applications to the conceptually related area of polymerizing chromatin regulators. To expand the theoretical basis for understanding how the oligomeric state of a transcriptional regulator influences its chromatin occupancy and function, we leveraged the extensive biochemical characterization of E26 transformation-specific factors to develop a mathematical model of Yan occupancy at chemical equilibrium. We find that spreading condensation from a specific binding site can take place in a path-independent manner given reasonable values of the free energies of specific and non-specific DNA binding and protein-protein cooperativity. Our calculations show that polymerization confers upon a transcription factor the unique ability to extend occupancy across DNA regions far from specific binding sites. In contrast, dimerization promotes recruitment to clustered binding sites and maximizes discrimination between specific and non-specific sites. We speculate that the association with non-specific DNA afforded by polymerization may enable regulatory behaviors that are well-suited to transcriptional repressors but perhaps incompatible with precise activation.

Introduction

Sequence-specific transcription factors (TFs) regulate the gene- expression programs that drive multi-cellular animal development. To achieve this, TFs combine protein-DNA and protein-protein interactions to assemble transcriptional regulatory complexes. Although protein-DNA interactions enable recognition of and binding to specific DNA sequences, a wide variety of homo- and heterotypic protein-protein interactions modulate DNA binding, promote associations between different TFs (1), and recruit co-activators (2) or co-repressors (3). Homo- or heterotypic dimerization is common among TFs, with notable examples including helix-loop-helix proteins (4), nuclear receptors (5), and TFs of the E26 transformation-specific (ETS) family (6). More broadly, the full spectrum of protein-protein interactions stabilizes occupancy of TF complexes at appropriate cis-regulatory elements and increases the combinatorial specificity and complexity for target gene regulation (7). Thus, understanding how both protein-DNA and protein-protein interactions determine TF occupancy is necessary for gaining molecular insight into the logic of development (8).

Notable among the various types of protein-protein interactions, certain classes of transcriptional regulators are capable of open-ended polymerization, forming large homotypic complexes (9). The effects of oligomerization beyond dimerization are not well-characterized from either a functional or a theoretical perspective, and most studies of polymerizing transcriptional regulators have focused on multi-member gene-silencing complexes that contain sequence-specific activities (10, 11). However, there is a class of polymerizing TFs that unite both sequence-specific DNA binding and homotypic self-association in one molecule, namely, members of the ETS family of TFs, Drosophila Yan and its human ortholog TEL or ETV6 (12, 13).

Yan and TEL are both transcriptional repressors that regulate gene expression downstream of receptor tyrosine kinase (RTK)/Ras/mitogen-activated protein kinase(MAPK) signaling (14, 15, 16). Both bind DNA in a sequence-specific fashion via their ETS DNA binding domain, and both also homotypically polymerize via a sterile alpha motif (SAM) domain (12, 13, 17). SAM-mediated self-association is required for the repressive function of both Yan and TEL, and measurements of diffusion kinetics in cultured Drosophila cells together with genetic rescue experiments argue for the presence and importance of SAM-dependent higher-order Yan complexes in vivo (12, 18).

Despite these indications of functional significance, whether the polymerizing ability of TFs like Yan and TEL can produce distinct DNA occupancy, and so confer novel regulatory potential, as compared to that of more conventional monomeric or dimeric TFs, is not known. Suggestively, chromatin immunoprecipitation experiments in Drosophila have shown that regions of Yan occupancy are quantitatively broader than most regions associated with sequence-specific TFs (19). Since direct in vivo measurements of the specific protein-protein and protein-DNA contacts that produce a particular chromatin binding profile is currently experimentally impossible, we turned to a modeling approach to gain insight into the mechanisms by which polymerization might drive the assembly of higher-order TF complexes on DNA.

The DNA occupancy of TFs has been modeled mathematically by a variety of approaches, most extensively using one-dimensional lattice models (20, 21, 22, 23) (reviewed in (24)). These models describe TF binding to long stretches of DNA at chemical equilibrium and have investigated questions concerning specific and non-specific binding, cooperative interactions among molecules, and orientation of binding sites. The thermodynamic feasibility of the nucleation and spreading of a sequence-specific, polymerizing TF remains uninvestigated. In this work, we present a model of Yan occupancy that recapitulates some of the features of Yan binding across the genome (19), and provides a framework to consider the occupancy of polymerizing TFs more broadly. We show that Yan occupancy can spread from specific recruitment sites to more distal sites at equilibrium, and that this behavior depends on both protein-DNA and protein-protein interactions. Additionally, we calculate the phase space for the behavior of systems that have different strengths of interaction, and we demonstrate that clustering recruitment sites increases Yan occupancy, even for the same strength of interactions and concentrations. Lastly, we demonstrate quantitative differences in the stability, size and sequence specificity of transcription complexes formed by polymerizing versus non-polymerizing TFs. Taken together, our results expand the approaches utilized for assessing TF occupancy and highlight distinct roles for polymerization in determining TF occupancy patterns at equilibrium.

Materials and Methods

Calculation of occupancy at equilibrium

We represent the genome as a series of discrete, potential binding sites for Yan arranged in a one-dimensional lattice, which we refer to as an element (Fig. 1 A). A pattern of Yan occupancy across an element is referred to as a microstate. At constant temperature and pressure, the fractional occupancy of a microstate, k, at equilibrium is given by

$$f_k=\frac{\text{exp}\left(-\Delta G_k/\text{RT}\right){\left[\text{Yan}\right]}^{a\left(k\right)}}{Z}.$$ (1)

In this case, ΔG_k is the change in Gibbs free energy upon Yan binding for microstate k, R is the gas constant (1.987204118 × 10³ kcal/mol degree), T is the absolute temperature (300° K for all calculations), [Yan] is the concentration of free molecules of Yan in the nucleus, a(k) is a function representing the number of bound Yan molecules in microstate k. The numerator of Eq. 1 is a Boltzmann weight for a given microstate. The partition function, Z, is the sum of Boltzmann weights for all microstates considered, and is given by

$$\text{Z}=\sum _{\mathit{k}}\text{exp}\left(-\Delta G_k/\text{RT}\right){\left[\text{Yan}\right]}^{\text{a}\left(\text{k}\right)}.$$ (2)

Figure 1.

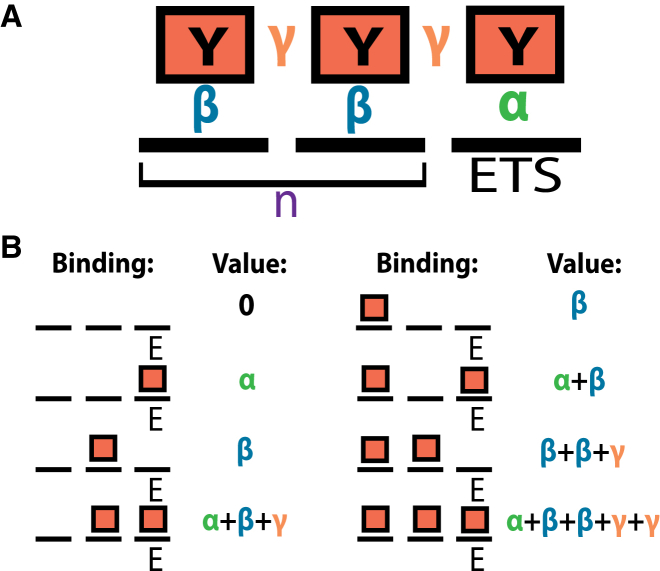
Lattice model for Yan binding at equilibrium. (A) Yan molecules (boxes) occupy discrete sites (bold black lines) at an element of DNA. The class of elements considered by the model contain one high-affinity specific binding site (ETS site) and n non-specific binding sites. Yan molecules participate in different types of interactions depending on their occupancy at the element, and the free energies of these interactions are given by the terms α, β, and γ. α represents the specific DNA binding free energy, β represents the non-specific DNA binding free energy, and γ represents the SAM-mediated protein-protein interaction free energy, contingent upon two molecules of Yan being adjacent to one another in the lattice. (B) Configurations of binding and free energy values for an element where n is equal to 2. The binary representation of the index of configurations (0,1,…,6,7) corresponds to the binding configuration itself. This provides a straightforward means of manipulating and scoring many microstates. Each microstate is shown with its free energy in terms of α, β, and γ. To see this figure in color, go online.

Binding sites within an element come in two types, specific and non-specific, with non-specific sites greatly outnumbering specific sites, which we refer to as ETS sites. ETS sites have a greater affinity for Yan binding than non-specific sites, and non-specific sites are taken to be of uniform, lower affinity for Yan, except where noted. Molecules of Yan can either be bound or unbound at each position on the element in a binary fashion, and each molecule of Yan can bind only a single site at one time. Unless otherwise noted in the text, we considered a class of elements characterized by one ETS site in the right-most position, flanked by n non-specific binding sites to the left. In this system, the total number of sites is n + 1, and the total number of microstates is equal to 2ⁿ⁺¹.

To calculate the fractional occupancy of microstates of interest, our model requires five parameters: α, β, γ, [Yan], and n (Fig. 1 A). α represents the change in Gibbs free energy of specific binding to ETS sites, whereas β represents the change in free energy of non-specific Yan binding to lower affinity sites. Given the affinity differences between the two types of binding sites, α will always have a lower ΔG than β. γ represents the change in free energy of association between two adjacent Yan molecules via their SAM domains. Reflecting Yan’s ability to polymerize, each additional adjacent Yan molecule contributes an additional increment of γ. The free energy of Yan binding is fully parameterized by α, β, and γ. Thus, the sum of interactions in a microstate, in terms of α, β, and γ, reflects the exact configuration of Yan molecules and defines the free energy of the microstate, ΔG_k.

The fractional occupancy of all microstates of a given element were calculated from k = 0 to k = 2ⁿ⁺¹ − 1. The free energies of all microstates of an element of length n + 1 can be calculated iteratively from smaller elements, from n = 0 up to the specified size. For the special case where n = 0, which corresponds to an element with just one ETS and no non-specific sites, there are only two free energies possible: ΔG_k=0 = 0 and ΔG_k=1 = α. The free energy of any microstate in an element of size n+1 (where n does not equal zero) is given by

$$\begin{array}{cc}\Delta G_{k,n+1}=\Delta G_{k,n}& \text{iff}\text{site}\mathit{n}+1\text{unbound}\\ =\Delta G_{k,n}+\beta & \text{iff}\text{site}\mathit{n}+1\text{bound}\mathrm{;site}\mathit{n}\text{unbound}\\ =\Delta G_{k,n}+\beta +\gamma & \text{iff}\text{site}\mathit{n}+1\text{bound}\mathrm{;site}\mathit{n}\text{bound}.\end{array}$$ (3)

The calculation was ordered in such a way that the molecular configuration of Yan molecules in a microstate was equivalent to the binary representation of the index of the microstate (Fig. 1 B). For instance, k = 5 represented in binary notation is 1 0 1, and k = 5 indexes a microstate where two bound Yan molecules are separated by one empty non-specific binding site. Microstates of interest can be returned by integral arithmetic operations on the index of the microstate. For example, the states where the ETS site is occupied are solutions of the equation k = 1 (mod 2), easily expressible in C++ by the elementary remainder operator, “%.”

Computation considerations

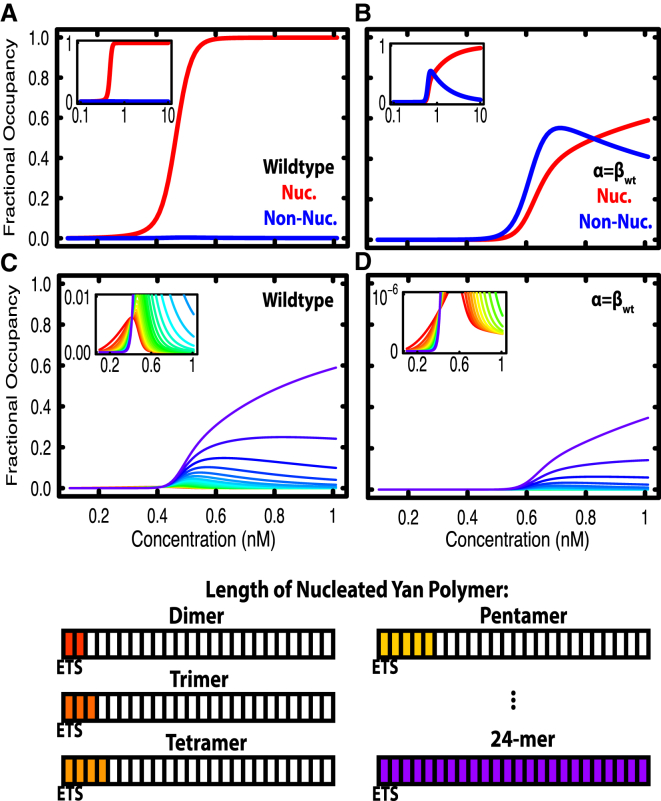
All calculations were performed using C++ compiled with gcc ver.4.4.7, and are available for download at https://uchicago.box.com/v/YanPolymerization, or by request. Unless otherwise noted, 24 site elements were chosen for computation. For an element of this size, there are 16,777,216 distinct microstates. For calculation of fractional occupancy by position within an element (see Figs. 2, 5, and 6), microstates were selected if they contained a bound Yan molecule at the position considered, which was implemented by bit-wise operations on the index of the microstate. For calculation of self-associated microstates (Fig. 3, A and B), microstates were counted if two or more molecules were adjacent to one another in the lattice, which was implemented by tracking adjacent positions with an integer flag. Microstates were counted if the adjacent position was occupied (i.e., the flag was raised) and the current position was occupied. Nucleated microstates (Fig. 3, A and B) were counted if the ETS site was occupied and a self-associated ligand was bound at the adjacent site. Thus, the expression “k%3==0” returns the set of microstates of interest. For calculation of exact nucleated chain length in Fig. 3, C and D, nucleated microstates were counted as before, with the additional caveat that the binding site adjacent to the end of the chain be unoccupied. In this way, nucleated chains of exactly x Yan molecules (but not x+1) can be counted—the only exception being the singular microstate with 24 self-associated molecules. It is important to note that microstates with chains of self-associated Yan molecules >x will be counted by this method; however, the measurement of fractional occupancy concerns nucleated microstates, which by definition requires binding at the ETS site, and not the broader set of self-associated microstates. For the calculation of spectral heat maps in Fig. 4, Boltzmann weights were calculated in log space to prevent overflow and then converted. Each spectral heat map represents 341 × 341 calculations.

Figure 2.

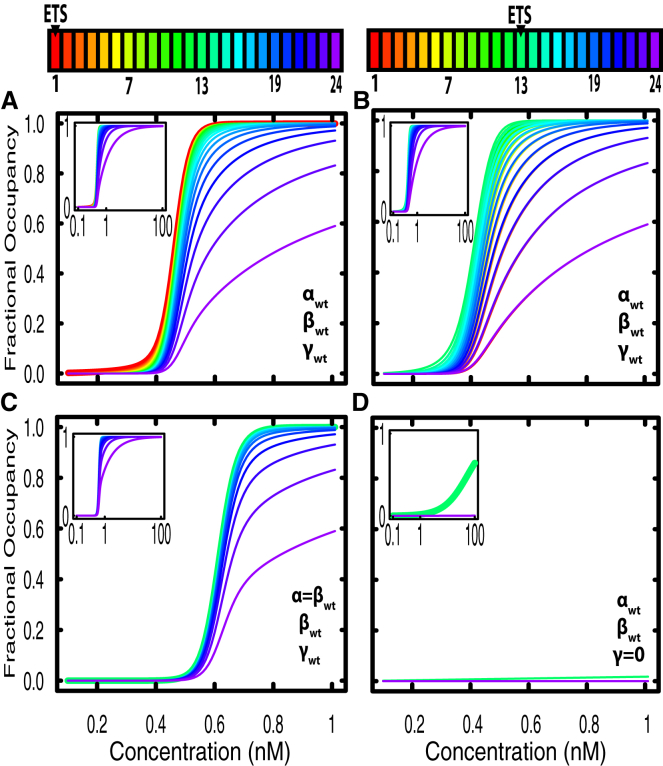
Yan occupancy spreads across the element at equilibrium and depends on both protein-DNA and protein-protein interactions. All plots show fractional occupancy of positions along a 24 site element as a function of concentration; insets plot the same data with concentration on a log scale. The ETS site is at position 1 in (A) and (C) and at position 13 in (B) and (D), as shown in the keys. (A) Site-by-site occupancy using the wild-type values for Yan binding parameters. Occupancy is highest at the ETS site (red) and progressively decreases at sites farther from the ETS, suggestive of a spreading profile. (B) Site-by-site occupancy for an element with the ETS site in the interior at position 13, using wild-type values for α, β, and γ. (C) Site-by-site occupancy when the specific DNA binding term is set equal to the wild-type value for non-specific binding, i.e., an element without any specific binding sites. Occupancy is highest in the center of the element (green) and decreases symmetrically from the center. (D) Site-by-site occupancy when the protein-protein interaction term (γ) is set to 0 kcal/mol. Significant occupancy is only observed at the ETS site for high concentrations (green curve at position 13). Note that identical lines are plotted on top of one another.

Figure 5.

Clustering multiple ETS sites within an element increases occupancy at the sites. One ETS site is held fixed, whereas another ETS site is moved from the adjacent position (orange) to the most distal position (purple). The plotted fractional occupancies are measured at the fixed ETS site as a function of concentration. Dashed lines denote fractional occupancy at the fixed site without an additional ETS site in the system. (A) Fractional occupancy with the wild-type parameters of Yan. (B) Fractional occupancy when the protein-protein interaction term is set to 0 kcal/mol. Note that all lines are identical in fractional occupancy and plotted on top of one another.

Figure 6.

Restricting Yan polymerization decreases occupancy at distal sites but maintains occupancy at specific sites, especially tandem ETS sites. Fractional occupancies are plotted as a function of concentration as in Fig. 2, with red curves representing the ETS site and purple curves representing the most distal site. Wild-type data from Fig. 2A are plotted as gray dashed lines. Wild-type parameters for α, β, and γ were used for all calculations. (A) Yan restricted to dimers (B) Yan restricted to trimers. (C) Yan restricted to tetramers. (D) Yan restricted to pentamers. (E and F) Fractional occupancy of Yan restricted to dimers, with multiple ETS sites. (E) Fractional occupancy at an element with two maximally separated ETS sites. Dashed lines are shown for some of positions 13–24 to show overlap of curves. (F) Fractional occupancy at an element with a tandem pair of ETS sites at positions 1 and 2.

Figure 3.

Occupancy of nucleated microstates depends on specific DNA binding of Yan. All graphs show fractional occupancy of types of Yan microstates as a function of concentration. Insets show the same data with concentration on a log scale (A and B) or a zoomed view of data at low fractional occupancies on a linear scale (C and D). (A) Fractional occupancy of nucleated microstates with two or more self-associated molecules versus that of non-nucleated microstates with two or more self-associated molecules, calculated for wild-type parameters. (B) Same as (A), but with specific DNA binding term set equal to the wild-type value for non-specific DNA binding. (C and D) Nucleated microstates with exactly x self-associated molecules. Values of x from 2 to 24 are shown. Colors progress through values of x, with red representing 2 and purple representing 24 (see key below the plots). (C) Fractional occupancy of nucleated microstates with exactly x self-associated molecules, for the wild-type parameters of Yan. (D) Same as (C), but with specific binding set equal to the wild-type value of non-specific binding. To see this figure in color, go online.

Figure 4.

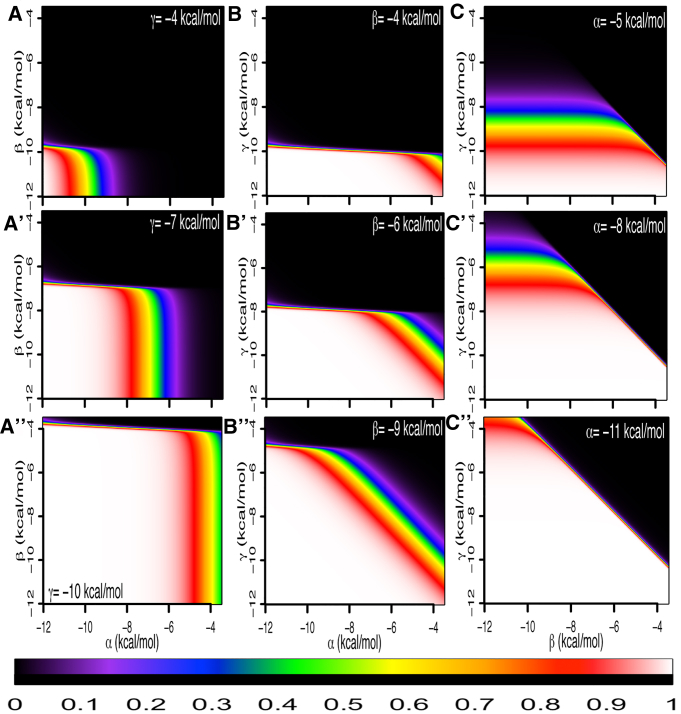
Exploration of parameter space for nucleated, self-associated microstates. All graphs are spectral heat maps plotting fractional occupancy of nucleated microstates with two or more self-associated molecules. Fractional occupancy of 0 is represented in black, and fractional occupancy increases moving through the visible color spectrum, ending with the fractional occupancy of 1 represented in white (see color key below). Values of the parameters α, β, and γ are plotted along the x or y axes from −3.5kcal/mol to −12.0 kcal/mol in 0.125 kcal/mol increments. All heat maps shown are calculated at a concentration of Yan of 0.1 nM. (A–A″) α versus β, with increasing values of γ shown from top to bottom (−4.0, −7.0, and −10.0 kcal/mol, respectively). (B–B″) α versus γ, with increasing values of β shown from top to bottom (−4.0, −6.0, and −9.0 kcal/mol, respectively). (C–C″) β versus γ, with increasing values of α shown from top to bottom (−5.0, −8.0, and −11.0 kcal/mol, respectively).

In calculations where the extent of Yan polymerization was restricted to dimers, trimers, tetramers, and pentamers (see Fig. 6), the free energy values of microstates were calculated in a different manner than specified in Eq. 3. Whereas each additional adjacent bound molecule contributes an additional increment of γ in all other calculations, when polymerization is restricted, values of γ are added up to the maximum permitted size of Yan complex. For example, when Yan is restricted to trimers, three adjacent molecules contribute two increments of γ to the free energy of a microstate, but an additional fourth adjacent molecule represents the start of a new trimer chain and does not contribute an additional increment of γ. Computationally, the extent of polymerization in a microstate was determined by a series of integer flags. Microstates were assumed to be making the maximum permitted number of protein-protein interactions allowed for the permitted size of the Yan complex. For example, four adjacent molecules were counted as “Y + Y + Y + Y” for unrestricted Yan polymers, where “+” denotes an interaction. However, when Yan was restricted to dimers, four adjacent molecules were counted as “Y + Y,Y + Y,” and not as “Y,Y + Y,Y,” which results in two values of γ added instead of one.

Results

Formulation of the model

We set out to develop a model of Yan binding at chemical equilibrium, utilizing this well-characterized protein to explore the role of polymerization in TF occupancy. Our model conceptualizes the genome as a series of binding sites for Yan, arranged in a one-dimensional lattice, which we refer to as an element (Fig. 1 A). In contrast to other one-dimensional lattice models of TF binding that consider an infinitely large genome (20, 23, 24), we calculated occupancy for a discrete element. Unless otherwise noted, the elements we calculate contain one specific binding site for Yan and n non-specific binding sites. This reflects our intuition that the majority of contacts a TF makes with DNA are not sequence specific, but instead are governed by weaker electrostatic interactions with the DNA phosphate backbone (25). Thus, higher-affinity sites, which we term ETS sites, make up a small fraction of the total sites and confer the sequence-specific contacts typical of ETS-family TFs, whereas lower-affinity non-specific sites make up the majority. Although our approach limits the scope of the binding region considered, it provides arbitrary control over the configuration of binding sites within the element, as well as the calculation of fractional occupancies of interest. Our model also incorporates parameters to represent Yan’s protein-DNA and SAM-mediated protein-protein interactions: α, β, and γ (Fig. 1 A). α represents the free energy value of specific binding to ETS sites, whereas β represents the free energy value of non-specific Yan binding to low-affinity sites. When two Yan molecules are adjacent to one another on an element, γ represents the free energy of a protein-protein interaction via their SAM domains. As Yan polymerizes, each additional adjacent Yan molecule contributes an additional increment of γ. Using this framework, the fractional occupancy of any microstate(s) of an element can be calculated as a function of four parameters: n, α, β, γ, and the concentration of Yan (Fig. 1 B; further details in Materials and Methods).

Parameterization and implementation of the model

Calculating the fractional occupancies of interest requires special consideration from a computational perspective. Because the number of microstates grows exponentially as n increases, the microstates must be generated and scored in an efficient, structured way. To minimize the complexity of the calculation, we utilized a binary notation scheme for ordering microstates. We assigned each microstate an integer index k, where k is a value from 0 to 2ⁿ⁺¹ − 1 whose binary representation reflects the molecular configuration of the microstate. Although ordering the calculation in this fashion does not reduce the computational complexity per se, the increased efficiency reduces the computing resources required.

To begin calculating fractional occupancies for Yan, we used the literature to parameterize the model with reasonable values of α, β, γ, and Yan concentration. Although there are no biochemical measurements of Yan’s specific or non-specific binding to DNA, these affinities have been measured for its human homolog, TEL, enabling us to assign values for α and β (26). Previous work has measured the affinity between two SAM molecules of Yan (27), which we used for γ. These values for α, β, and γ (−9.955, −5.837, and −7.043 kcal/mol, respectively) are referred to as the wild-type parameters, α_wt, β_wt, and γ_wt. Lastly, there are no published measurements of nuclear Yan concentration, but based on measurements of other TFs (28), we set a reasonable range of concentrations from 0.1 to 100 nM.

To determine what size of element would permit exploration of the broad-scale features of Yan occupancy without requiring exorbitant amounts of memory to track microstates, we explored Yan binding across the range of element sizes n = 2–23; a subset of these fractional occupancy curves are shown in Fig. S1 in the Supporting Material. At low values of n (Fig. S1, A and B), Yan binding curves were shallow across all concentrations calculated. As n increases, the binding profiles sharpened quickly. At elements of size n = 19–22 (Fig. S1, F–I), the sharpening slowed significantly, with these elements showing highly similar profiles. We also plotted the concentrations of 50% fractional occupancy for specific sites across the collection of elements in the size range n = 2–23 (Fig. S2). Elements with low values of n (1–5) required higher concentrations of Yan to attain 50% fractional occupancy, but as n increased, all positions measured asymptotically approached a value of ∼0.4 nM. Therefore, we selected 24 site elements (n = 23) for all further calculations, because the Yan fractional occupancy profile was representative of the larger set of fractional occupancy curves, and the computational cost was deemed reasonable.

Yan occupancy spreads across the element at equilibrium

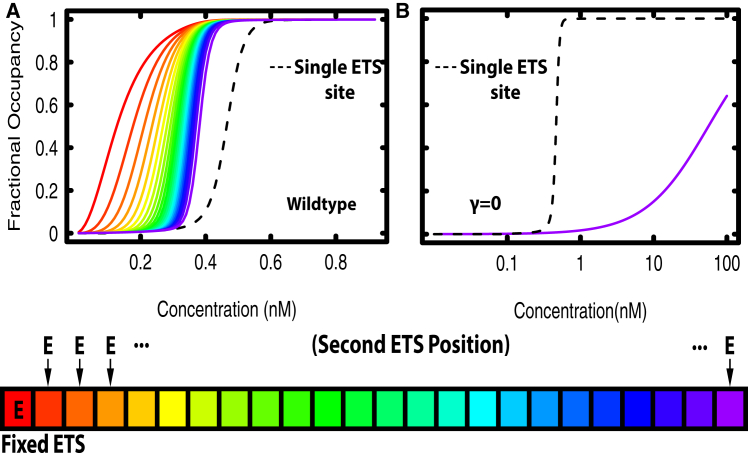
Genome-wide chromatin immunoprecipitation studies of Yan occupancy have noted extensive bound regions that are larger than those typically occupied by other Drosophila TFs (19, 29). To ask whether our model could recapitulate and explain this feature, we calculated Yan occupancy across an element at equilibrium over a range of concentrations. Microstates were counted if they contained a bound Yan molecule at a given position on the element, starting at the ETS site and moving outward to the most distal site of the element. The results show that Yan fractional occupancy at all positions increased with concentration and saturated to completion (Fig. 2 A).

Interestingly, we noted a middle regime of concentrations where Yan preferentially occupied the ETS site with progressively less occupancy at sites further from the ETS site. This suggests that Yan can generate a broad binding profile across the element, and can do so at chemical equilibrium without requiring active mechanisms to establish this type of profile. We hypothesized that this could be explained by contiguous chains of Yan molecules nucleating at the ETS site and spreading outward toward distal, non-specific sites. To rule out the possibility that edge effects might be producing this behavior, we repeated the calculation for an element of the same size, but with the ETS site in the middle (Fig. 2 B). Yan occupancy spread outwards bi-directionally and equally from the ETS site and was not affected by the position of the ETS site within the element. Highest occupancy occurred at the ETS site (position 13, light green curve). Because the ETS site is positioned slightly asymmetrically in the center of the element, there was marginally higher fractional occupancy in positions 14–24 versus 1–12 (seen most clearly from 0.4 to 0.6 nM). Based on these results, we conclude that the broad chromatin occupancy profiles of Yan observed in vivo could reflect binding at equilibrium.

Next, we assessed the sensitivity of the spreading pattern to changes in the strength of Yan’s protein-DNA and protein-protein interactions. First, we explored the impact of Yan’s protein-DNA interactions by varying α and β, the specific and non-specific DNA binding parameters. As a control, we set α and β equal to 0 kcal/mol, thus eliminating Yan protein-DNA interactions. No occupancy was detected at any of the concentrations considered (Fig. S3 A), confirming that protein-protein interactions alone are insufficient to drive occupancy. To explore the contribution of sequence-specific DNA binding, we set α equal to β_wt to represent an element with no ETS site and then recalculated Yan occupancy. In contrast to the preferential occupancy at the ETS site and spreading to the most distal site, observed with the wild-type parameters (Fig. 2 A), in the absence of a high-affinity ETS site, maximal occupancy occurred at the middle positions of the element and then tapered distally in both directions (Fig. 2 C). This suggests that Yan is condensed on DNA, but that binding is not nucleated from the ETS site.

We also examined the role of the protein-protein interaction term γ in driving Yan fractional occupancy. When γ was set to 0 kcal/mol and α and β were held at their wild-type values, occupancy at non-specific sites was reduced to nearly zero at all concentrations, and even the ETS site was only half occupied at a Yan concentration of 100 nM (Fig. 2 D). The position of the ETS site had no effect on occupancy when the protein-protein interaction term was set to 0 (Fig. S3 B), validating the essential contribution of SAM-mediated interactions. Additionally, we varied the strength of protein-protein interaction across a wide range from 0 to –12 kcal/mol and saw that this parameter strongly influenced occupancy across the element (Fig. S4). At weak values of γ (−5 to −6 kcal/mol, Fig. S4, A–C) there was almost no occupancy, whereas at strong values of γ (−8 to –9 kcal/mol; Fig. S4, G–I), the element was completely occupied at every site. In a narrow middle regime of protein-protein affinities (−6.5 to −7.5 kcal/mol; Fig. S4, D–F,), the spreading profile was observed. Fractional occupancy profiles with more extreme values of γ represented a continuation of the corresponding curves in Fig. S4 (data not shown).

Taken together, these results highlight distinct roles for protein-DNA and protein-protein interactions in influencing Yan occupancy across the element. Both non-specific protein-DNA interactions and protein-protein interactions contribute strongly to Yan fractional occupancy. In contrast, specific DNA binding interactions contribute modestly to the level of occupancy, but impact the shape of the distribution by increasing occupancy at specific binding sites. Therefore, we hypothesize that specific DNA binding may facilitate recruitment to certain regions of the genome, whereas non-specific DNA binding may allow for spreading into more distal positions.

Nucleated microstates drive Yan fractional occupancy

One mechanism that could produce the observed occupancy profiles is contiguous chains of Yan spreading across the element via SAM-mediated interactions. To test this idea, we investigated which microstates contribute most strongly to the spreading profiles by calculating the fractional occupancy of “self-associated” microstates, which we define as microstates that have at least one contiguous chain of two or more Yan molecules. This definition encompasses dimers, trimers, and so on, up to a chain that spans the entire element. The terms “nucleated” and “non-nucleated” in reference to the self-associated microstates distinguish those in which the chain of Yan molecules includes the ETS site from those in which it does not. Because nucleated and non-nucleated microstates are mutually exclusive sets, non-nucleated microstates can be calculated by removing nucleated microstates from the set of all self-associated microstates.

To explore further the role of sequence-specific binding interactions in nucleating Yan occupancy, we compared all self-associated, nucleated, and non-nucleated microstates under different conditions for α and β. When compared using the wild-type Yan parameters, nucleated microstates and self-associated microstates contributed almost equally to Yan occupancy, with non-nucleated microstates contributing negligibly across all concentrations (Fig. 3 A). When α is equal to β_wt, meaning there is no contribution from sequence-specific interactions, nucleated microstates made up a much smaller proportion of the self-associated microstates until saturation was reached at ∼10 nM (Fig. 3 B). There was also a middle regime of concentrations where non-nucleated microstates were more likely than nucleated microstates (∼0.5–0.8 nM), indicating that under these conditions, chains of Yan molecules are condensed on the element but are not nucleated by the ETS site. This confirms that condensation can occur with just non-specific DNA binding, and suggests that removing the relative advantage of specific DNA binding allows microstates that do not encompass the ETS site to predominate. Thus, α biases the distribution of bound molecules toward nucleated binding at the ETS site.

Next we measured the exact distribution of chain lengths for nucleated microstates. As shown in Fig. 3 C, the fractional occupancy of nucleated microstates with exactly x molecules was plotted, up to 24 self-associated molecules. At low concentrations (<0.4 nM), nucleated chains of two molecules were the most likely and chains of 24 molecules the least likely. At ∼0.4 nM, all curves passed through a single point of equal fractional occupancy, and at higher concentrations, chains of 24 molecules were the most likely nucleated microstates (Fig. 3 C). When we repeated the calculation with α equal to β_wt (Fig. 3 D), there was weaker fractional occupancy for all chain lengths considered. In addition, the low-concentration-regime behavior had significantly lower fractional occupancy (compare scales of 0–0.01 and 0–0.00001 in the insets of Fig. 3, C and D), and the point where all curves have equal fractional occupancy occurred at the same concentration of Yan. We conclude that chain length within nucleated microstates follows the broader trend of Yan occupancy with respect to concentration—at low concentration, the number of Yan molecules is limiting, and at a high concentration, large chain lengths predominate. This relationship holds true when α is equal to β_wt, even though fractional occupancies are decreased across the board.

Exploration of parameter space

Our initial results suggested distinct roles for protein-DNA and protein-protein interactions in determining Yan binding across the element. To test the relationships between these interactions, we systematically co-varied α, β, and γ and reiterated the calculation over a wide area of parameter space. The fractional occupancies of all nucleated microstates for a given parameter set were calculated and plotted as a spectral heat map. We fixed Yan concentration at 0.1 nM for all spectral heat maps shown in Fig. 4, because at this concentration, the broad trends upon changing α, β, and γ are most easily distinguished.

We first mapped the relationship between α and β as γ was increased (Fig. 4 A). At lower values of both α and β, nucleated fractional occupancy was increased. Consistent with non-specific interactions contributing more strongly to occupancy than specific interactions (Fig. 2), occupancy increased sharply for small increases in β (e.g., −6.75 kcal/mol to −7 kcal/mol (Fig. 4 A′)) as compared to α, for which occupancy increased slowly over a wide range of values (e.g., −5 kcal/mol to −9 kcal/mol, Fig. 4 A′). However, once occupancy was achieved at a given value of α, additional strengthening of β did not change the nucleated fractional occupancy. Thus, without non-specific DNA binding interactions, significant occupancy cannot be achieved; specific DNA binding interactions instead determine the extent to which binding occurs at the ETS versus other positions. Increasing the strength of γ resulted in greater nucleated occupancy. Specifically, as γ was increased, the sharp transition in occupancy occurred at weaker values of β, although the total width of the transition in α was unaffected (i.e., the overall shape of the map translocates to the upper right corner, but does not sharpen or change shape; compare Fig. 4 A to Fig. 4 A′ and Fig. 4 A′ to Fig. 4 A″). This was also the case if Yan concentration was increased—the sharp transition in β occurred at lower values, whereas the transition in α was unaffected (Fig. S5, A–A″).

We next examined the relationship between α and γ with increasing strength of β (Fig. 4 B). Nucleated occupancy increased by strengthening all three parameters. Reminiscent of the plots in Fig. 4, A–A″, there was a sharp transition in occupancy for γ (−7.75 kcal/mol to −8.0 kcal/mol (Fig. 4 B′)) and a broad, fixed-width transition for α. However, this transition was along a diagonal slope, suggesting a compensatory trade-off between α and γ. This suggests that γ plays a role in increasing both occupancy at the element and nucleated occupancy, in contrast to β, where strengthening the interaction increases occupancy but not nucleated occupancy. Neither the width of the transition in α nor the sharpness of the transition in γ changed as the strength of β increased, and increasing Yan concentration maintained these relationships (Fig. S5, B–B″).

Lastly, we plotted the relationship between β and γ as α was increased (Fig. 4, C–C″). The nucleated fractional occupancy did not depend on the value of β as evidenced by the horizontal stripes of color, representing a wide range of values of β (analogous to the vertical stripes in Fig. 4, A–A″). Additionally, the negative slope of the diagonal suggested a compensatory trade-off for β and γ in determining occupancy, meaning that the same occupancy was achieved by strengthening γ and weakening β (and vice versa). Increasing the strength of α translocated the figure toward higher fractional occupancy but kept the same steepness of the transition. At increased concentrations, the shape of the graph translocated, but the sharpness of the transition in α was unchanged (Fig. S5, C–C″). Taken all together, these results suggest that β and γ are both required for occupancy at the element, and that loss of strength in one interaction can be compensated by increasing the other; α does not have a dominating role in determining occupancy. In contrast, in the context of nucleated occupancy, α plays an important role and has a compensatory relationship with γ, whereas β is less influential.

Spreading is robust to variation in non-specific binding

In the calculations described above, the non-specific DNA binding affinity term β represented sequence-independent electrostatic binding to the DNA phosphate backbone but ignored the effects of sequence heterogeneity. To capture the assumption that DNA binding at non-consensus sites will occur with a range of affinities according to differences in nucleotide content, we next asked how sensitive the patterns of Yan occupancy are to variation in non-specific DNA binding. Using the wild-type value of β as a minimum threshold, we drew values of β from a half-Gaussian distribution with a fixed standard deviation to create random non-specific sites with varying affinities, and then recalculated Yan occupancy. Increasing the variation in β by increasing the standard deviation gradually shifted the profile toward greater occupancy at lower concentrations, eventually producing profiles where non-specific sites had greater occupancy than the ETS site (Fig. S6, A–C). To quantify the point where variation overwhelms the normal spreading profile, we varied the standard deviation of β and calculated occupancy for 100 random elements for each value. At the concentration where the ETS site is at half-maximal occupancy, we compared fractional occupancy of all other positions to the ETS site—if the ETS site had greater occupancy than any other position, we considered the spreading profile to be intact. Fig. S6 D shows the fraction of elements with spreading profiles for various values of the standard deviation. At a value of 0.6, which corresponds to up to a 55-fold increase in affinity in β (−5.837 kcal/mol to −8.287 kcal/mol), nucleated spreading was as likely to occur as not to occur. As a 55-fold increase in affinity approaches that of a sequence-specific binding interaction, the calculation provides a complete exploration of the effects of non-specific binding across the plausible affinity range. Therefore, we conclude that the spreading pattern is robust with respect to heterogeneity in non-specific DNA binding.

Clustering of multiple ETS sites increases fractional occupancy

Given that TF binding sites tend to be clustered into regulatory elements (30), the number and spacing between ETS binding sites could play important roles in determining Yan occupancy. We therefore expanded the model to include two specific ETS binding sites separated by an integer number of non-specific binding sites. Using the wild-type parameters, we repeatedly calculated fractional occupancy at one ETS site as the second ETS site was moved step-wise from the opposite end of the element toward the first site, and then plotted this as a function of Yan concentration (Fig. 5). Occupancy at the first ETS site increased as the opposing site was moved closer, with maximal occupancy achieved when the two sites were arranged as a tandem repeat. In all configurations, occupancy at two-site elements was greater than that at a single-site element (Fig. 5 A). Thus, clustering transcription binding sites increases their occupancy in a distance-dependent manner. To confirm the role of protein-protein interactions in generating this behavior, we repeated the calculation when γ equals 0 kcal/mol, and found that the distance-dependent increase in occupancy disappeared (Fig. 5 B). We conclude that the arrangement of binding sites relative to one another within an element can stabilize occupancy in a manner that depends on protein-protein interactions bridging the binding sites.

We also noted in the wild-type parameter calculation that as the two ETS sites were brought together, the slope of the occupancy curves became less sharp (Fig. 5 A). This suggests that site clustering exerts a stronger effect on weakly or partially occupied binding sites as compared to strongly occupied binding sites—for example, fractional occupancy of 0.1 is achieved at an ∼6-fold lower concentration by clustering sites (0.05 versus 0.35 nM), whereas fractional occupancy of 0.9 is achieved at an ∼1.5-fold lower concentration by clustering (0.27 versus 0.42 nM). Therefore, clustering TF binding sites may preferentially result in partial occupancy of these sites at equilibrium, consistent with an emerging role for the conservation and function of medium- to weak-affinity TF binding sites in regulatory element function (31, 32, 33).

Restricting the extent of Yan polymerization results in preferential occupancy at specific sites

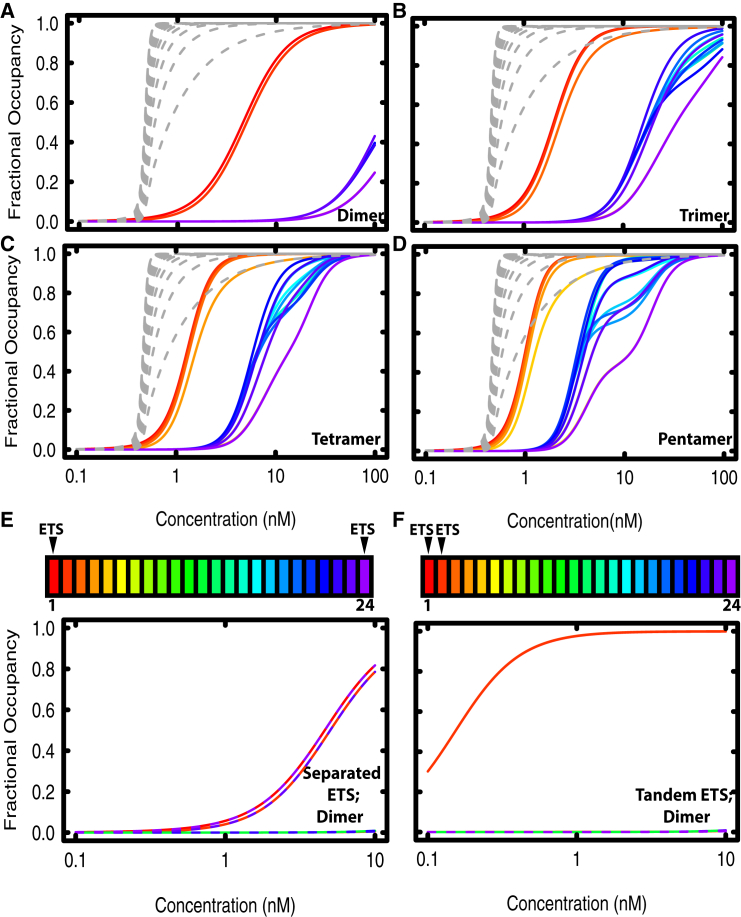
Because many TFs operate as dimers, we asked which features of the Yan occupancy profiles could be explained by dimeric interactions and which required higher-order polymerization. When we limited Yan to forming dimeric complexes, occupancy was dramatically reduced for all sites across an element (Fig. 6 A, solid lines) as compared to polymeric Yan (Fig. 6 A, dashed lines; coloring by position across the element is the same as in Fig. 2). Interestingly, there was strong occupancy at the ETS site and the immediately adjacent non-specific site, and greatly reduced occupancy at all other sites. For example, focusing on the concentration regime around 10 nM, fractional occupancies were ∼0.9 for the ETS and adjacent site (red solid lines), but near 0 elsewhere (blue/purple solid lines). These results predict that TFs that typically dimerize will have strikingly different chromatin occupancy profiles compared to those that polymerize. Specifically, dimers will only stably occupy specific DNA binding sites, whereas polymers can condense on DNA in the absence of specific binding interactions (Fig. 2 C). Additionally, the relative difference between binding at specific versus non-specific sites was much greater for dimers than for polymers. Although the fractional occupancy of a dimer was lower than that of a polymer at a given Yan concentration, dimers were better able to discriminate between specific binding sites and non-specific sites, and did so over a wide concentration range.

Fig. 6, B–D, shows the results of extending the calculation to consider trimers, tetramers, and pentamers. Occupancy remained decreased relative to polymers, but increased relative to dimers. Similar to the pattern with dimers, there was strong occupancy at the ETS site and immediately adjacent sites, but far less occupancy at all other sites. The gap in occupancy between the ETS adjacent sites and all other sites decreased as the extent of polymerization increased, suggesting that the ability to discriminate between specific and non-specific sites decreases as polymerization increases. For trimers and above, the fractional occupancy curves at distal sites were not smooth sigmoids, but showed more complicated behavior that arises from edge effects at the end of the element. For example, a trimer cannot fit into two vacant sites near the edge of the region modeled. Such numerical artifacts were not observed in earlier calculations (Fig. 2 B), because polymers fill the element completely, with no partial chains at the edge. Taken together, these results suggest that Yan’s spreading profile is highly dependent on the extent of polymerization and, by extension, that typical dimerizing TFs will exhibit significantly different DNA occupancy profiles under the same conditions.

Given that recruitment to specific sites was reduced for dimers compared to polymers, we asked if clustering of ETS sites could restore occupancy to the level observed for the polymer. To do so, we compared occupancy of Yan dimers across two elements, one in which the two ETS sites were maximally separated and one in which the two ETS sites were immediately adjacent. Similar to the single ETS element calculations (Fig. 6, A–D), Yan dimers were recruited equally to the separated ETS sites and to sites immediately adjacent to the ETS sites, whereas occupancy at all other sites was negligible (Fig. 6 E). In contrast, when ETS sites were placed immediately adjacent to one another, occupancy was much higher at both sites and rivaled the recruitment to tandem sites observed with polymers (compare Fig. 6 F to Fig. 5 A). We conclude that Yan dimers and polymers can exhibit equivalent recruitment to a tandem pair of ETS sites, but not to single ETS sites.

Discussion

In this study, we describe a mathematical model of Yan DNA binding that provides, to our knowledge, a new framework for understanding Yan’s in vivo occupancy patterns and for exploring the unique behaviors that polymerization can confer to a TF. We find that Yan occupancy spreads across DNA at equilibrium, and that this behavior shows distinct requirements for both protein-DNA and protein-protein interactions. More broadly, our results predict that a polymerizing versus non-polymerizing TF will form different kinds of complexes on a given enhancer element, with respect to both the degree of occupancy and the requirement for sequence-specific DNA binding sites. We propose that a key role of polymerization is to recruit and stabilize TF accumulation across regions of an enhancer that lack specific binding sites. In contrast, DNA occupancy of monomeric or dimeric TFs is more tightly restricted to specific sites of recruitment. This result may offer insight into why so many TFs have evolved to operate as dimers and further suggests that emphasizing the contributions of tandem versus individual binding sites might improve the success of both bioinformatic predictions and experimental manipulations of enhancers. We also note that although the model was formulated for Yan, it extends in principle to any TF or combinations of interacting TFs, with the only differences in the precise values of α, β, or γ.

A major conclusion from our calculations is that polymerization-driven TF spreading across DNA can occur at equilibrium. The traditional assumption is that TFs are first recruited to DNA via recognition of high-affinity sequence-specific binding sites and then spread via protein-protein interactions. Our model similarly predicts highest occupancy at specific sites with decreasing occupancy distally, but reveals that a precise, step-wise kinetic process is not required to produce such a profile. Instead, our model is path independent, which suggests that spreading of a polymerizing TF occurs because it is thermodynamically most favorable, and that non-polymerizing TFs do not spread primarily because the complexes are thermodynamically less favorable. This finding also bears implications for the spreading of repressive chromatin complexes assembled by either the Polycomb group (PcG) proteins or the silent information regulator (SIR) factors (10, 11). Traditionally, these systems have been thought to function analogously to polymerizing TFs in that they are recruited by specific binding of one protein (to a DNA sequence or histone mark), followed by binding and polymerization of another protein (34). However, there is also thought to be a requirement for cycles of action, such as recruiting the histone modification enzyme that installs the original mark, thus resulting in a positive feedback loop (34). Our results suggest that, in addition to those kinetic processes, the binding profile of spreading regulators could be substantially influenced by polymerization at equilibrium, depending on the strength of protein-DNA and protein-protein interactions. Conversely, the occupancy patterns of a polymerizing TF like Yan or TEL will almost certainly be modified by cycles of post-translational modification, recruitment of cofactors and other TFs, and perhaps interactions with PcG or other polymerized repressive complexes. Supporting the notion of heteropolymeric repressive complexes, the polymerizing PcG protein L(3)MBT has been shown to complex directly with TEL1 via a SAM-SAM interaction (35, 36).

Based on the thermodynamics of binding at equilibrium, we speculate further that the distinct occupancy patterns calculated for a polymerizing TF produce intrinsically repressive regulatory behavior that is perhaps incompatible with the precise activating regulation of gene expression. First, our results suggest that multimerization can be viewed as a trade-off between occupancy and discrimination of proper binding sites; as the extent of polymerization increases, the gap between specific and non-specific occupancy narrows. Because activating TFs may have a greater requirement for binding precision, restricting them to dimers enables the sharpest distinction in occupancy of specific versus non-specific sites. In contrast, repressors may use both active sequence-specific mechanisms and passive sequence-non-specific mechanisms of gene regulation. In the latter scenario, TF polymerization would drive the spreading of oligomeric complexes into distal, non-specific sites on DNA, thereby effectively occluding access to other factors, both repressive and activating. Although a polymerized activator would have a similar effect, because activating complexes are often comprised of collectives of different TFs bound to clustered specific binding sites in enhancers, with the combinatorics of binding important for regulatory specificity (37), general steric interference would seem counterproductive, as it would either inappropriately repress gene expression or lead to uncontrolled activation. As noted above in the text, clustering of binding sites produces a greater fold increase in occupancy for lower-affinity sites as opposed to higher-affinity sites (Fig. 5 A), which may explain the preference for clustered, weak sites in driving transcriptional activation in some developmental enhancers (31, 32, 33). Given that introduction of high-affinity binding sites has been shown to disrupt the expression patterns of these enhancers, either by reducing levels of expression or by inducing ectopic expression, it is reasonable to assume that excess TF occupancy may be deleterious at these elements. Therefore, polymerization might be counterproductive not only for reducing binding-site discrimination, but also for globally increasing occupancy beyond threshold levels at sensitive developmental enhancers.

In this context, it is interesting to consider the role that polymerization might play in transcriptional mis-regulation driving oncogenesis (38). Translocations involving the TEL/ETV6 gene (the human homolog of Yan) are prevalent in human leukemia, and several of these link the N-terminal exons that encode the polymerizing SAM in frame to other TFs. For example, the most common cause of childhood acute lymphoblastic leukemia is a reciprocal translocation that fuses the TEL SAM onto the RUNX family TF AML1 (38). Mechanistically, we hypothesize that conversion of AML1 into a polymerizing TF may permit spreading into regions of chromatin it would not usually occupy. Although the conversion to polymerizing TF could also fundamentally alter AML1 transcriptional activity, even absent an activity change, altered occupancy on DNA could substantially dysregulate the cell’s transcriptional program and lead to oncogenesis.

Although translocations involving TEL are thought to generate polymerizing repressive complexes, a handful of oncogenic translocations that target other TFs are hypothesized to generate polymerizing activating complexes. Prime examples are the reciprocal translocations that fuse the polymerizing low-complexity transactivation domains of the TET-family proteins, Ewing sarcoma protein or fused in Ewing sarcoma, with the DNA-binding domain of the ETS-family members FLI1 or ERG (39, 40). Based on our modeling results, we speculate that the reduced requirement for sequence-specific binding associated with polymerization will produce more promiscuous hyper-activating complexes. If correct, this would argue that TF polymerization is compatible with repression but not with precise activation of transcription.

Returning to Yan, our observation that the polymerization state of Yan can facilitate the formation of distinct complexes on DNA has explanatory power for several aspects of Yan biology. First, experiments comparing the extent of polymerization required for full in vivo function have concluded that although Yan monomers have extremely limited repressive ability, Yan dimers are almost, but perhaps not quite, as functional as wild-type polymerization-capable Yan (12, 19). Parallel experiments addressing this question for human TEL have similarly concluded that dimerization confers significant, but not complete, function (18). Based on our model, we speculate that the relatively strong recruitment of Yan/TEL dimers to clustered, specific binding sites may be sufficient to execute a majority of their transcriptional regulatory functions. However, at certain enhancers and/or in specific developmental contexts, the broader occupancy conferred by polymerization must confer biologically significant regulation.

Second, polymerization at equilibrium could theoretically explain some features of actual Yan chromatin occupancy patterns. Briefly, a meta-analysis of chromatin occupancy patterns of Drosophila TFs concluded that Yan DNA-bound regions are broader than those associated with typical non-polymerizing TFs (19). Consistent with our findings that clustering of specific binding sites can increase Yan occupancy, the top 600 Yan-bound peaks showed enrichment in terms of both the number of ETS sites and the number of clustered ETS sites (19). To consider how our model of polymerization at equilibrium might explain observed peaks, we consider the prominent subset of extensively Yan-bound regions termed high-density regions (HDRs). Yan HDRs were measured to be 4 kb in length; taking into account that chromatin immunoprecipitation of sonicated DNA fragments will define regions broader than those actually bound by the TF (41), the actual length of an average HDR might be closer to 3 kb. The ETS domain of TEL (Yan’s human homolog) bound to specific DNA has been crystallized and was shown to have a footprint of ∼10 bp (26), which would translate to 240 bp of consecutive footprints for a 24 site element. In vitro DNA binding analyses have shown that TEL dimers can bind cooperatively to ETS sites separated by up to 50 bp (42), which if true in vivo, could increase the size of bound regions by about a factor of 5, permitting occupancy up to 1500 bp in length. Our model is agnostic to the actual conformation of DNA, and so if one assumes that short stretches of intervening DNA can be looped out without impacting polymerizing interactions, then the effective binding range might increase further. Assuming that these estimates are reasonably accurate, then a majority of the broad, Yan-binding peaks observed could be explained by polymerization at equilibrium. Additionally, we note that our previous work comparing the genome-wide occupancy profile of Yan monomers to that of wild-type Yan showed that the median size of Yan HDRs was reduced by ∼20% (19). This indicates that polymerization contributes to the Yan occupancy profile, but it suggests that additional interactions contribute to the ultimate binding pattern. We speculate that cooperation with other transcriptional regulatory complexes could stabilize Yan monomer binding and lead to an underestimate of the contribution of polymerization at equilibrium to Yan occupancy. Given that Yan operates in a milieu that includes many other TFs, future iterations of our model will incorporate cooperative and competitive interactions with other TFs that could positively or negatively influence polymerization-driven Yan occupancy.

Author Contributions

M.H., I.R., and J.R. designed experiments; M.H. and J.R. wrote the code; M.H. performed the experiments; M.H., I.R., and J.R. analyzed data; M.H., I.R., and J.R. wrote the article.

Editor: Stanislav Shvartsman.