Capturing a Dynamic Chaperone–Substrate Interaction Using NMR-Informed Molecular Modeling

Abstract

Chaperones maintain a healthy proteome by preventing aggregation and by aiding in protein folding. Precisely how chaperones influence the conformational properties of their substrates, however, remains unclear. To achieve a detailed description of dynamic chaperone–substrate interactions, we fused site-specific NMR information with coarse-grained simulations. Our model system is the binding and folding of a chaperone substrate, immunity protein 7 (Im7), with the chaperone Spy. We first used an automated procedure in which NMR chemical shifts inform the construction of system-specific force fields that describe each partner individually. The models of the two binding partners are then combined to perform simulations on the chaperone–substrate complex. The binding simulations show excellent agreement with experimental data from multiple biophysical measurements. Upon binding, Im7 interacts with a mixture of hydrophobic and hydrophilic residues on Spy's surface, causing conformational exchange within Im7 to slow down as Im7 folds. Meanwhile, the motion of Spy's flexible loop region increases, allowing for better interaction with different substrate conformations, and helping offset losses in Im7 conformational dynamics that occur upon binding and folding. Spy then preferentially releases Im7 into a well-folded state. Our strategy has enabled a residue-level description of a dynamic chaperone–substrate interaction, improving our understanding of how chaperones facilitate substrate folding. More broadly, we validate our approach using two other binding partners, showing that this approach provides a general platform from which to investigate other flexible biomolecular complexes through the integration of NMR data with efficient computational models.

Graphical abstract

Introduction

Maintaining a healthy proteome is of great importance to proper cellular function and disease prevention.^1–3 Molecular chaperones play an important role in regulating the proteome by facilitating the folding of nascent polypeptide chains, preventing protein aggregation under stress conditions, and helping proteins refold during and after stress. Despite the clear importance of chaperones, achieving a detailed understanding of the mechanisms by which chaperones interact with their substrate proteins has proven to be a particularly difficult endeavor.^4,5 Most chaperones function as a part of large mega-Dalton-sized molecular machines, whose size, complexity, and ATP or co-chaperone dependence complicates analysis.^6,7 However, chaperone activity is not limited to these large, complex systems. Here, we investigate the mechanism of Spy, a 16 kDa chaperone that functions in the periplasm of Escherichia coli. Expression of Spy is induced by protein unfolding conditions.⁸ In vivo and in vitro experiments demonstrate that Spy both prevents protein aggregation and aids in protein refolding in the absence of ATP or any other high-energy cofactors.⁹ Super Spy mutants that show improved chaperone activity are generally less stable than wild-type Spy, suggesting that conformational disorder plays a role in Spy's chaperone mechanism.⁹ While several types of biochemical data suggest that Spy binds substrates within its cradle, they only provide a low-resolution description of the mode of Spy–substrate binding.⁹

Conformational dynamics is thought to be an efficient way to handle the high conformational diversity involved in chaperone–substrate interactions.¹⁰ However, achieving a detailed view of chaperone–substrate interaction is very difficult, in part due to the diversity of substrates that chaperones recognize, and in part because these substrates are often primarily partially unfolded. Given Spy's compact size and autonomous chaperone activity, it represents an attractive model system: a biophysically amenable, minimal chaperone that can be used to investigate the conformational dynamics underlying chaperone–substrate binding in detail. The principles underlying Spy's chaperone action may be informative for larger, more complex, and much less biophysically amenable chaperone–substrate pairs. Toward helping to elucidate the basic principles of chaperone–substrate binding, we recently solved the crystal structure of Spy in complex with the minimal Spy-binding portion of the in vivo and in vitro substrate immunity protein 7 (Im7).¹¹ In this structural model, Im7 was bound in several different conformations. Recently, we also probed the kinetics of Spy–Im7 interaction, and found that Im7 can fold itself while bound to Spy.^12,13 Here, we combine NMR and molecular simulations to investigate the detailed conformational dynamics underlying Spy–Im7 interaction in solution.

NMR is exquisitely suited to investigate protein conformational flexibility and protein–substrate interactions at residue-level resolution. Although several previous efforts have characterized chaperone–substrate interactions using NMR,^14–22 most chaperone–substrate pairs are large, challenging systems for NMR, and thus only a few high-resolution descriptions of chaperone–substrate conformational changes and dynamics are currently available.^20,21 These studies are informative and have identified several properties of chaperone–substrate binding and have provided insights into the chaperone-induced changes in folding kinetics and intermediate states sampled along the folding pathway. Despite these advances, exactly how the chaperone modifies the conformational landscape of the substrate and how the substrate transits between different substates remains elusive. To investigate these crucial questions and obtain complementary mechanistic information about chaperone–substrate interactions, we used a multi-pronged approach that combines straightforward NMR measurements and molecular dynamics (MD) simulations to characterize the interaction of the chaperone Spy with its substrate Im7.

Combining NMR and MD simulations has proved to be a successful strategy for studying conformational flexibility and molecular recognition and is therefore a promising way to investigate flexible complexes.^23–28 While the long time scale conformational dynamics accompanying flexible molecular recognition generally prohibits the use of detailed, all-atom MD simulations, coarse-grained methods permit a more efficient exploration of the conformational landscape.^29,30 Such minimalist models play a crucial role in testing ideas about the forces governing protein folding and recognition^31–33 and have been shown to accurately recapitulate experimental folding^34–36 and binding mechanisms.^37–39 In particular, native topology-based (or “Gō-like”) coarse-grained models have emerged as an effective approach for characterizing in residue-resolution detail the binding mechanisms of intrinsically disordered proteins (IDPs) for which an experimental structure of the IDP–partner complex exists.^40–44

Here, we harness the potential of coarse-grained modeling in combination with site-specific NMR measurements to achieve a high-resolution, dynamic description of chaperone–substrate interaction. We introduce a strategy that treats the force field as a mathematical encoding of the physical chemistry of a particular system, incorporating system-dependent experimental data. We use a Gō-like model⁴⁵ to describe our system at the amino acid level and create a system-informed force field by optimizing the model parametrization for the individual binding partners using NMR¹³C chemical shift data.⁴⁶ We then perform simulations of the chaperone–substrate complex using the optimized parametrizations of the two binding partners. These simulations are then validated by monitoring the changes in NMR peak intensities upon complex formation and by obtaining multiple other biophysical measurements. This approach allows us to characterize, in detail, the dynamic behaviors of bound and unbound Im7 constructs and to provide new insights into the mechanism of chaperone–substrate interaction. We find that this interaction is characterized by a redistribution of conformational flexibility, not just between the substrate and the chaperone, but within the chaperone itself. Our combination of site-specific NMR measurements and coarse-grained modeling was also tested and validated on two other model systems, implying it may readily be applied to other complex biological systems to help understand their structure and dynamics.

Results and Discussion

Im7_6–45 Conformational Properties Elucidated through NMR

In our study of the Spy–Im7 chaperone–substrate complex, we used an Im7 fragment consisting of residues 6–45 (Im7_6–45), the same fragment that we had previously shown encompasses the entire Spy-binding domain.^8,9 By itself in solution, Im7_6–45 exhibits the chemical shift signature of a mainly unfolded peptide (Figure S1). The backbone assignments of Im7_6–45 in solution were readily obtained using standard triple-resonance NMR experiments.⁴⁷ This helicity profile, computed here as a per-residue secondary structure propensity (SSP) from ¹³C chemical shifts,⁴⁸ indicates that Im7_6–45 remains mainly unfolded in solution (overall helicity of 21%) with residual helical elements (up to 40%) observed in the regions corresponding to helices in the crystal structure of full-length Im7⁴⁹ (Figure 1A). This observation is supported by longitudinal (R₁) and transverse (R₂) ¹⁵N spin relaxation rates and {¹H}-¹⁵N heteronuclear nuclear Overhauser effect (NOE) measurements^50,51 (Figure 1A). Thus, while being primarily unfolded, Im7_6–45 in solution contains residual structure reminiscent of folded Im7.

Figure 1.

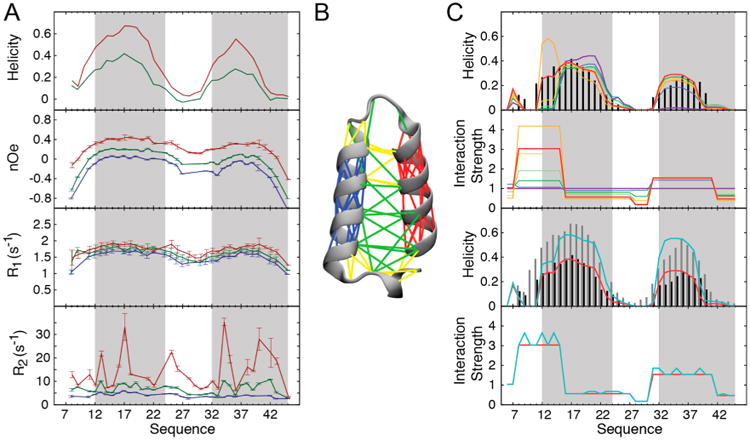
NMR measurements describe site-specific conformational properties of the Im7_6–45 substrate and permit a system-informed force field optimization. (A) Site-specific NMR measurements characterize Im7_6–45 conformational properties under different ionic strengths. From top to bottom: helical propensity determined as the secondary structure propensity (SSP) score using ¹³C secondary chemical shifts, {¹H}-¹⁵N heteronuclear nuclear Overhauser effect (NOE), longitudinal relaxation rates (R₁), and transverse relaxation rates (R₂), measured at 298 K at 14.1 T (600 MHz ¹H Larmor frequency). The protein gains helical structure with increasing salt concentration: 4 mM sodium phosphate (blue), 4 mM sodium phosphate and 50 mM NaCl (green), and 10 mM sodium phosphate and 150 mM NaCl (red). Gray boxes correspond to the positions of the helices in the crystal structure of full-length, wild-type Im7. (B) Native interactions defined in the Gō-like coarse-grained model of Im7_6–45, which is built based on residues 6–45 in the full-length Im7 crystal structure (PDB ID: 1CEI). This model was the starting point for optimization of the Im7_6–45 force field. The lines depicted on the 6–45 fragment represent local interactions within the N-terminal helix (blue), C-terminal helix (red), or other regions (yellow). Longer-range interactions are shown in green. (C) Renormalization of the strength of the interactions in the Gō-like model for Im7_6–45 based on the NMR-determined SSP score. First, we optimized the coarse-grained model against the low-salt SSP profile (top two graphs). At each iteration, the scaling factors of the interactions in the force field (lower graph) are reweighted to improve reproduction of the experimental SSP profile (upper graph): initial values (violet) and iterations 1 (blue), 2 (dark green), 3 (light green), 4 (yellow), 5 (orange), 6 (red), and the experimental targeted SSP profile (black). Iterative optimization of the interaction strengths results in a force field that reproduces the experimental profile. The model is then validated using high ionic strength data (two bottom graphs). At high salt, Im7_6–45 exhibits a higher level of helicity (gray). This effect is captured by optimizing a single additional parameter that modulates any interaction involving at least one charged residue (turquoise).

We then attempted to analyze the changes in conformation that occur in Im7_6–45 upon binding to Spy. Unfortunately, addition of Spy resulted in substantial NMR peak intensity losses within Im7_6–45, suggesting a significant contribution of chemical exchange due to complex formation (see Chaperone–Substrate Interaction, below) (Figure 2A). The exchange contributions were significant enough to eliminate the possibility of directly observing the complex by traditional NMR means. To circumvent this issue and obtain details about the Spy–Im7_6–45 interaction, we developed an alternate computational approach that was informed by NMR data for the individual partners. In this approach, we optimized the MD force fields of the interacting partners in an automated fashion using residue-resolution NMR data obtained for each partner independently. We then used these optimized force fields along with the binding affinity (K_d) of Spy–Im7_6–45 interaction to describe the conformational dynamics of the complex.^42,43,52 We also successfully applied this new approach to two other dynamic protein complexes (see below), suggesting that this strategy will be generally useful to examine flexible proteins and protein complexes whose characterization was formerly difficult.

Figure 2.

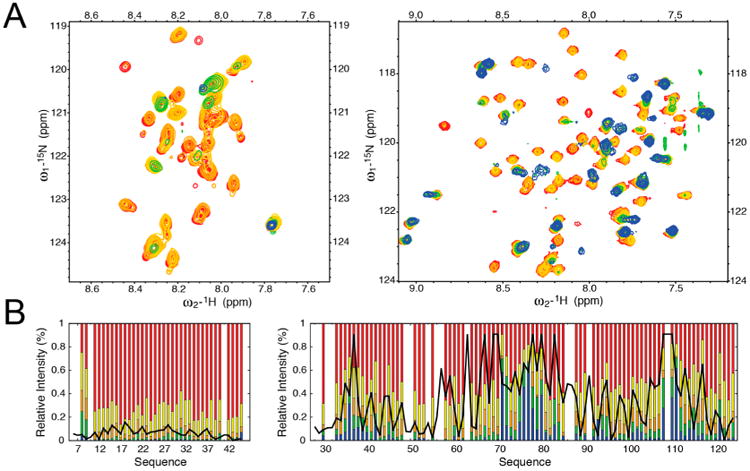
NMR titration of the Spy–Im7_6–45 interaction. (A) ¹⁵N HSQC spectra are shown for protein ratios of 0 (red), 0.1 (yellow), 0.2 (orange), 0.3 (green), and 0.4 (blue) when unlabeled Spy was added to labeled Im7_6–45 (left) and unlabeled Im7_6–45 was added to labeled Spy (right). Addition of Spy results in the significant loss of intensity for several peaks in Im7_6–45, precluding the possibility of a direct characterization of chaperone–substrate interactions by NMR alone. (B) Comparison of changes in NMR signal intensities from titration experiments to the chaperone and substrate interaction patterns observed in the binding simulations. Relative intensities, compared to the free forms, of the resonances observed in Im7_6–45 (left) and Spy (right) upon titration. Color-coding is the same as in (A). Black lines correspond to the pseudoenergy of contact between Spy and Im7_6–45 (arbitrary units) obtained from coarse-grained simulation of the complex using the optimized force field. Low values indicate favorable regions for chaperone–substrate interactions.

Building an NMR-Informed Force Field of a Partially Unfolded Substrate

To investigate the binding and folding of Im7_6–45 in the presence of Spy, we first needed to obtain an accurate coarse-grained molecular model for the partially folded substrate Im7_6–45. The force field used for simulating Im7_6–45 conformational properties is essentially a Gō-like model:^42,45 a coarse-grained description in which each residue is treated as a single bead, and the interactions between the beads are constructed based on a structural model⁴⁵ (see Methods and Figure 1B). In this case, the force field was further modified by decreasing the propensity of the force-field to overstabilize α-helices to better account for the mainly unfolded nature of Im7_6–45,⁴¹ as simply parametrizing the model against a folded structure of Im7 would not capture the mainly unfolded nature of Im7_6–45 as indicated by NMR measurements (Figure 1A). Using this initial parametrization ensures that, by itself, Im7_6–45 remains mainly unfolded in our simulations, with any residual structure stemming from the structural properties of the full-length Im7 native structure. However, simulations using this initial model did not accurately recapitulate the residual helical propensities of Im7_6–45. Most notably, the initial model (Figure 1C, violet line) did not display the appropriate level of helicity when compared to the experimental SSP profile (Figure 1C, black bars) in the entire C-terminal helical region, and parts of the N-terminal helical region. This initial simulation therefore resulted in an overall underestimation of Im7_6–45 helicity, as observed by NMR and circular dichroism (CD) spectroscopy (see below). We thus embarked upon improving this generic coarse-grained description of Im7_6–45 using NMR data, inspired by analogous all-atom MD force-field refinements previously performed using NMR data.^46,53

Overall, the approach uses NMR chemical shifts to encode site-specific experimental information for each of the binding partners (the chaperone Spy and its substrate Im7). This strategy creates system-specific force fields accurate enough to capture the conformational behavior of each partner individually. It is then possible to take advantage of this improvement to perform binding simulations involving the two partners.

Specifically, we used the experimental data measured for Im7_6–45, namely the per-residue helical propensity, to directly guide the modeling of Im7_6–45. Our initial parametrization of Im7_6–45 contains 88 inter-residue nonbonded interactions that could be renormalized to better describe Im7_6–45 behavior (Figure 1). As the experimental data consists of 40 SSP scores (one per Im7_6–45 residue), the optimization of a scaling factor for 88 separate interactions would be underdetermined. Therefore, we devised an optimization procedure that requires many fewer parameters to describe the residue-level helicity of Im7_6–45. This simulation exhibited six consecutive segments in which the helicity was contiguously under- or overestimated (Figure 1C). To minimize the number of parameters to optimize, we used only six parameters to renormalize the entire network of nonbonded interactions by using the same scaling factor for every residue within a single segment. These scaling factors are then combined via the geometric mean and applied to the pairwise interactions (see Methods). It has previously been shown that rescaling too strongly can induce some distortion in the obtained parametrization and can adversely affect the resulting models.⁵³ We therefore performed this optimization in an iterative manner. To minimize distortions, we rescaled as conservatively as possible, using a harmonic restraint to prevent excessive individual reweighting (Methods). At each step, starting from the previous sampling, the six parameters were optimized to produce a reweighting of the Im7_6–45 MD ensemble that minimizes the variance between the experimental and simulated helicity profile of Im7_6–45 (Figure 1C). After six iterations, the approach converged to excellent agreement (considering the simplicity of the model) with the experimental secondary structure profile (Table S1 and Figure S2A). Thus, by introducing only a limited number of parameters, we achieved a computationally efficient optimization procedure for constructing protein-specific force fields from a generic force field.

To test the robustness of the optimized Im7_6–45 force field, we modeled Im7_6–45 conformational dynamics under an alternative environmental condition, namely, at higher ionic strength. Im7_6–45 contains many charged residues (three lysines, four aspartic acids, and six glutamic acids), suggesting that under high-salt conditions, electrostatic screening should substantially affect Im7_6–45 properties. We therefore experimentally investigated the effect of ionic strength on Im7_6–45 conformation. Under high-salt conditions, the overall experimental helicity profile remains similar in shape to the profile seen under low-salt conditions, but the magnitude of the helicity significantly increases (Figure 1). This increase in helicity is also observed in the slight but consistent concomitant increases in R₁ and NOE relaxation rates. Interestingly, significant changes in R₂ are also observed, suggesting the presence of conformational exchange.⁵¹ The increase in R₂ correlates well with the magnitude of the ¹⁵N chemical shift perturbations seen with increasing ionic strength (Figure S3). These observations suggest that Im7_6–45 could be in exchange between the mainly unfolded state, primarily observed at low salt, and a more structured state that becomes more populated at higher ionic strength. If the force field optimized for low-salt conditions is robust, a minimal change in its parametrization to account for this new environment should be able to recapitulate the increase in helicity experimentally observed at higher salt concentrations. To test this possibility, we introduced a single scaling parameter, α, designed to modulate electrostatic interactions based on solution ionic strength conditions (Methods). This parameter scales any nonbonded interactions in Im7_6–45 that involve at least one charged residue,^52,54 which account for roughly half of all the interactions in the coarsegrained model for this system. With an optimized value of α, the coarse-grained simulations produce a helicity profile that matches very well with experiment (Figures 1C and S2B), indicating that a minimal perturbation to the optimized force field effectively recapitulates the effect of salt on Im7_6–45 conformational dynamics. Interestingly, the determined value of 1.2 for α corresponds to an effective increase in attraction between charged residues within Im7_6–45. Since many of the contacts are between residues with like charges, increasing the strength of the nonbonded interactions (α > 1) allows these like-charged pairs to interact more strongly than in the case without the α parameter. This effect reflects electrostatic screening in the model, as increasing the nonbonded attraction between charged pairs allows Im7_6–45 to overcome repulsive interactions and adopt more structure. Recapitulating Im7_6–45 properties at high salt using only a single additional parameter to encode electrostatic-screening effects suggests that our parametrization is robust and can be used to investigate Im7_6–45 under different conditions, such as binding to the chaperone Spy.

Preparing the Chaperone for Simulation

To characterize Spy so that it may be used in subsequent binding simulations, we used a classical triple-resonance-based strategy to assign 93% of the backbone spin system of Spy⁴⁷ (Figure S4). Unassigned resonances are clustered at the N terminus and within the flexible linker region. Analysis of ¹³C secondary chemical shifts reveals that Spy's structure consists mainly of four consecutive helices, and that the position and size of these helices are in excellent agreement with the X-ray crystal structure of Spy⁸ (Figure S5).

To investigate the dynamic properties of Spy via NMR, we measured the R₁ and R₂ ¹⁵N spin relaxation rates and {¹H}-¹⁵N NOE at two different magnetic field strengths (600 and 800 MHz ¹H Larmor frequencies)^50,51 (Figure S6A). Model-free analysis of the relaxation data^55,56 suggested that the structure of Spy in solution is in agreement with its apo crystal structure (Figure S6 and Tables S2–S4)⁸ in that Spy forms a well-folded helical structure that does not display large-scale motions. Diminished order parameters, slow motions and exchange contributions in the loops and the C terminus of Spy indicate higher amplitude motions in these regions (Figure S6B, Table S3, and S4). Additionally notable dynamics was observed for Thr108, located in the loop preceding the last α-helix, and exchange contribution at both magnetic fields were seen for Val76, which is located at the very beginning of the third helix. The lack of major motions within Spy also suggests that the crystal structure represents a good structural model of Spy in solution with dynamic regions restricted to loops and the C terminus.

Due to the agreement of Spy's crystal structure with the NMR measurements, we decided to use Spy's unbound crystal structure⁸ as the basis for constructing a Gō-like model⁴⁵ of the chaperone (Figure S5A). Minor adjustments in weighting the local flexibility and nonbonded interactions were used to optimize the simulation,⁴² including helping to ensure that Spy remains in its dimeric state over the time scale of the simulations (Methods). This model properly recapitulated Spy's experimentally measured conformational properties with the exception of a slight overestimation of the overall degree of helicity, especially in the second helix (Figure S5B). Note that the trajectory was run at 300 K, whereas the experimental data were recorded at 313 K, which is closer to Spy's melting temperature of 321 K.⁹ Spy could thus be subject to some local unfolding at the higher temperature relative to the lower temperature, explaining the slight differences in the observed versus predicted helicity levels. We chose to parametrize the Spy coarse-grained model at the same temperature as we did for the Im7_6–45 substrate (300 K) so that we could later combine the Spy and Im7 models for our investigation of chaperone–substrate interaction.

Back-calculating Spy NMR chemical shifts directly from the coarse-grained Spy trajectory (i.e., without performing a computationally expensive all-atom reconstruction) shows excellent agreement with the measured chemical shift values, within or close to the estimated accuracy of the predictor⁵⁷ (Figure S5B and Table S5). This agreement further suggests that we obtained a suitable description of Spy at the coarsegrained level and that further optimization would probably not lead to a significant improvement in the molecular description of Spy dynamics. We therefore used this model for Spy along with the NMR-informed force field for Im7_6–45 to investigate the details of chaperone–substrate interactions.

Testing the Generality and Accuracy of the Approach for Binding Simulations

To analyze binding and folding events, we reasoned that we could combine the system-specific force-field parametrization for each individual binding partner with a generic interprotein potential (Methods). The effective strength of the interprotein potential would then be renormalized using a single parameter, such that the trajectory of the complex contained the correct proportion of free and bound snapshots based on the experimentally measured dissociation constant (Methods).^42,58 We then evaluated this strategy using well-characterized published complexes to test the accuracy of the approach, as well as to test whether the approach is general and transferable. Toward that aim, we selected two model systems for which detailed NMR characterization was previously obtained. (Detailed methods and results are presented in the Test of the Approach on Known Complexes section in the Supporting Information.)

We first considered the interaction between the phosphorylated kinase-inducible domain (pKID) of the cAMP response-element binding protein (CBP) and the KID-binding domain (KIX) of the CREB binding protein.^59,60 It was previously shown that pKID forms an initial encounter complex with KIX before reaching its fully folded bound state.⁶⁰ Using our optimization approach, we were able to correctly predict overall properties of both the binding-and-folding pathway as well as the final complex structure (Supporting Information) arising from previous NMR investigation.^59,60

Second, we investigated the partially folded C-terminal domain of the nucleoprotein of the Sendai virus (Ntail) and its biological partner, the C-terminal subdomain of the phoshoprotein (PX).^61,62 Upon force-field optimization, we were able to recapitulate the conformational exchange of Ntail between different helices as previously identified using NMR residual dipolar couplings,⁶¹ and also observe a shift of population of those helices upon interaction with PX in agreement with existing relaxation-dispersion data (Supporting Information).⁶²

These results indicate that our approach, in which we use no information about the bound state other the dissociation constant, can capture the major features of the interaction mode and binding mechanism for various systems, further supporting our strategy and its general use for flexible complexes, including the Spy:Im7 system.

Chaperone–Substrate Interaction

As mentioned above, addition of sub-stoichiometric quantities of Spy to labeled Im7_6–45 caused a large and rather uniform decrease in NMR signal intensity across the entire spectrum, with very small chemical shift changes, indicative of intermediate exchange regime dynamics (Figure 2A). Further addition of the partner to reach full saturation of the complex and to potentially overcome this unfavorable exchange regime⁵¹ did not lead to any significant improvement in the spectra. The converse experiment, in which unlabeled Im7_6–45 was added to labeled Spy, yielded similar results (Figure 2A). As these results precluded further straightforward NMR experiments, we attempted an alternative approach to describe the dynamics of this chaperone–substrate system utilizing our knowledge of the individual binding components. Employing the same strategy as our test complexes that took into account the experimentally determined dissociation constant, we obtained a model of the chaperone–substrate interaction by combining 10 independent binding simulations.

Experimental Validations of Spy–Im7 Interactions

Before analyzing the details of the Spy:Im7 interactions and dynamics, we extensively validated the binding simulations by experiments, as presented in Table 1. The overall good agreement between simulation and experiment suggest that the simulations will provide useful insights into the Spy:Im7 complex.

Table 1. Evaluating the Consistency of the MD Simulations with Experimental Observations.

no.	experiment	experimental observation	observation from optimized force field (unoptimized force field)	comments
1a	CD/NMR of Im76–45 by itself	11%/21% helicity	15% helicity (unoptimized: 10%)	this is the only observation that was used to optimize the individual force fields
2a	CD of Spy:Im76–45, subtracting CD spectrum of Spy alone	40% helicity of Im76–45 while in complex with Spy	36% helicity of Im76–45 while in complex with Spy (unoptimized: 23%)	increased agreement after optimization
3a	CD of Spy:Im76–45	+29 pp change in Im76–45 helicity upon bindingb	+21 pp change in Im76–45 helicity upon binding (unoptimized: +13 pp)	calculated from observations 1 and 3; increased agreement after optimization
4a	NMR titrations of Spy:Im76–45	see Figure 2 for per-residue intensity decreases of Spy	similar patterns observed in the frequency of contact between Spy and Im76–45	see the Contact Maps section in Supporting Methods and Figure S8
5c	X-ray crystallography	51% of residues on the concave surface of Spy participate in Im76–45 binding, compared to 12% of residues in other regions	51% of residues on the concave surface of Spy participate in Im76–45 binding, compared to 2% of residues in other regions (unoptimized: 31%/2%)	See the Interaction Patterns section in Supporting Methods and Figure S7
6c	X-ray crystallography	Spy dimer twists by −9° upon Im76–45 binding, as defined by an interdomain dihedral angle	Spy dimer twists, on average, by −4.6° along this same dihedral angle while bound to Im76–45	intramolecular Spy force field is the same in the optimized and unoptimized simulations, Figure 4
7c	X-ray crystallography	flexible linker region (residues 47–57) more disordered upon Im76–45 binding	upon binding, per-residue fluctuations increased by ∼50% relative to the unbound state for several residues in the flexible linker region	see comment for observation 6, Figure 4
8d	kinetics of Im7 folding while bound to Spy	binding to Spy slows down both folding and unfolding of full-length Im76–45 by approximately an order of magnitude	binding to Spy slows down folding (by a factor of 2) and unfolding (by a factor of 5) of the Im76–45 substrate	network analysis only performed for the optimized simulations, Figure 5
9e	genetic selections to increase Spy chaperone activity	mutants either increase concave surface hydrophobicity, or potentially increase flexibility of linker region	binding occurs primarily within cradle, and flexible linker region increases motion in bound state	see Site-Specific Description of Chaperone–Substrate Interactions
10e	in vitro cross-linking of Spy and Im76–45	all cross-links indicate binding to concave surface	see item 5 above
11e	in vitro H/D exchange and proteolysis of Spy upon Im76–45 binding	several residues on Spy's concave surface are protected upon binding	Spy interacts with Im76–45 through its concave surface	see Site-Specific Description of Chaperone–Substrate Interactions

^aThis study.

^bpp = percentage points.

^cRef 11.

^dRef 13.

^eRef 9.

To compare the interactions between Im7 and Spy with data from other sources, we built a detailed inter-residue pairwise contact map that shows how Spy interacts with Im7_6–45 (Supporting Information). The resulting contact map (Figure 3A) reveals that Spy interacts with Im7_6–45 mainly through two regions, the inner parts of the cradle and its flexible loop (Figure 3B). On the other hand, Im7_6–45 exhibits much lower selectivity in its interaction pattern. Comparison of this contact pattern with the interaction pattern derived from our recent crystallographic analysis¹¹ of the Spy–Im7_6–45 ensemble shows very good agreement (Figure S7 and Tables 1 and 2). The breadth of the interactions demonstrates that Spy uses a combination of hydrophobic and hydrophilic residues to contact Im7. This heterogeneity could be important for Im7 folding while bound to Spy.⁶³

Figure 3.

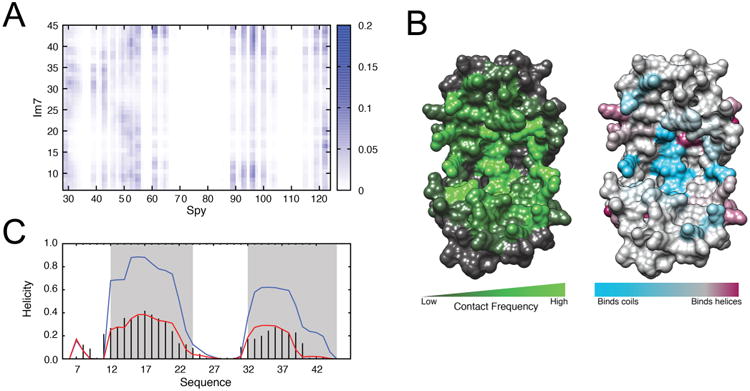
Chaperone–substrate interaction pattern from simulation. (A) Contact map reporting on the frequency of interaction between Spy and Im7_6–45 residues, color-coded from 0 (white, no interaction) to 0.2 (blue, most frequent interaction sites). (B) Left: Visualization of the contact pattern on the Spy chaperone, constructed by projecting the contact frequency in (A) onto the Spy crystal structure. Spy residues colored in green contact the Im7_6–45 substrate frequently during the binding simulations, whereas the residues colored in gray do not. The convex side of Spy does not form significant contacts with Im7_6–45 (Figure S7). Right: Propensity for Spy residues to bind unstructured (cyan) or helical residues (maroon) within Im7_6–45. (C) Change in per-residue helical propensity of Im7_6–45 upon binding, indicating that Im7_6–45 becomes more structured upon binding to Spy. The experimental and simulated helicity profiles for free Im7_6–45 are shown by black bars and the red curve, respectively. The helicity profile for bound Im7_6–45 from simulation is shown in blue.

Table 2. Fractional Composition of Spy Residues Interacting with Im7_6–45.

		simulations
category	X-raya	optimized	unoptimized
concave surfaceb	0.51	0.51	0.31
convex surface	0.12	0.02	0.02
concave surface and hydrophobic	0.38	0.31	0.19
concave surface and hydrophilic	0.61	0.65	0.39

^aRef 11.

^bIn total, 39 residues were determined to reside on the concave surface of Spy (See the Interaction Patterns section in Supporting Methods). All other residues are considered part of the convex surface. Of the 39 residues on the concave surface, 16 are hydrophobic and 23 are hydrophilic. Within the concave surface, we consider how often hydrophobic and hydrophilic residues interact with Im7_6–45 in the bottom two rows.

As a validation of our binding simulations, we projected the simulation contact map along the Spy and Im7_6–45 sequences and converted it into a pseudo-energy of interaction that reports on the frequency at which a given residue of Spy or Im7_6–45 can interact with any residue of its partner. This pseudo-contact energy profile agrees well with the decreases in intensity measured by NMR in the titration experiments (Figures 2B; Table 1), suggesting that the model of interaction derived from our simulations recapitulates the NMR site-specific information observed for this chaperone–substrate complex. Thus, the disappearances of NMR signals appear to be primarily due to the direct interaction between the two partners, which is supported by the qualitative correlation between the Spy–Im7_6–45 contact pattern and the intensity loss pattern (Figure S8). Both the NMR intensity decreases and computational modeling indicate that for Spy, the most prominent, favorable interaction sites (i.e., largest decreases in intensities) are in the cradle, including the inner helices and the flexible loops. Conversely, the least favorable interaction sites (i.e., smallest decreases in intensity) in Spy upon addition of Im7_6–45 are located only on the backside of Spy and in the hinge preceding the C-terminal helix, the two regions farthest away from the interior of the cradle. The Spy–Im7_6–45 interaction pattern from simulation is additionally in agreement with previous cross-linking, mutational, biophysical, and crystallographic data, which indicate that Spy uses its concave surface for substrate binding^8,9,11 (Table 1). This good agreement to multiple, independent experimental measurements suggests that the binding simulations obtained using our system-specific force fields of Spy and Im7_6–45 recapitulate the experimentally observed binding pattern.

For comparison, we also performed Spy–Im7_6–45 binding simulations with the initial, unoptimized force field for the substrate. Using this unoptimized force field, we observe a lower degree of Im7_6–45 secondary structure in the bound state that does not match well with experimental data. Specifically, when using our optimized force field, the overall level of helicity of Im7_6–45 in the complex is 0.36 (Figure 3C and Table 1), which is in excellent agreement with CD measurements that estimate a value of 0.40 (Figure S9). On the other hand, using the initial force field for the peptide with no optimization yields a notably less structured substrate (0.23 fraction helicity) in the bound state (Table 1). That the adequate increase in helicity upon binding is only observed after parametrization optimization demonstrates its necessity for accurately modeling Im7_6–45 in complex with Spy.

While the overall interaction patterns observed from the simulations using the optimized and unoptimized parameters are similar (i.e., the substrate primarily interacts with the Spy cradle), the detailed pattern of interaction differs between the two simulations. This difference is particularly obvious in the distribution of Spy residues involved in the interaction with Im7_6–45. Similar to the crystal structure,¹¹ the Spy cradle is more extensively involved in substrate interaction than other regions of the chaperone in our optimized binding simulations compared to the unoptimized simulations (Table 2). Within the cradle, the fraction of hydrophobic and hydrophilic residues that participate in substrate interaction is also comparable between X-ray and the optimized simulations (Table 2).

Overall, the available CD, crystallography, and NMR data reporting on the Spy–Im7 interaction (none of which were used in building our model) consistently suggest that our use of simple NMR data for the individual binding components to optimize the force field significantly improved simulation of the complex. Combined with the success of this approach in describing two previously established biological complexes, this high level of agreement between the optimized simulations and independent Spy–Im7 experiments (Table 1) suggests that the proposed molecular description is suitable for further analysis of the chaperone–substrate interaction.

Site-Specific Description of Chaperone–Substrate Interactions

We analyzed the Spy–Im7_6–45 interaction pattern to assess the Spy residues that exhibit the highest contact levels with the Im7_6–45 substrate (Figure 3). In particular, we were interested in evaluating the role of charged residues in Spy–Im7_6–45 binding, as we recently found that the Spy–Im7 interaction is strongly dependent upon ionic strength.¹² Strikingly, in the optimized simulations, arginines constitute many of the Spy residues that substantially interact with Im7_6–45. Of the seven total arginines in the Spy construct used for simulation, six of them are among the 11 highest contact scores. Arg122, Arg55, and Arg61 exhibit three of the top five scores and reside within the flexible C-terminus or linker region. Arg122 and Arg61 correspond to residues that were protected upon trypsin cleavage while Im7 was bound to Spy.⁹ Thus, our model suggests that this protection was due primarily to direct interaction of these residues with the substrate, instead of indirectly through conformational change in the chaperone. Arg122, Arg55, and Arg61 are all conserved,⁹ and in the future it would be interesting to mutate them in order to probe their specific involvement in substrate binding and folding. Further supporting the importance of electrostatics in chaperone–substrate interaction, several negatively charged residues in the Im7_6–45 substrate (Asp9, Glu12, and Glu39) exhibit the highest contact frequencies with Spy.

The other two top-five ranking contacting residues in Spy are His96 and Gln100. Intriguingly, we previously found through genetic selections that mutation of these two residues to leucine enhanced chaperone activity.⁹ While both His96 and Gln100 make significant contact with hydrophilic residues in Im7_6–45 during simulation, they are also frequently in close proximity to several hydrophobic residues (Leu38, Phe41, Val42, and Ile44) in the substrate. Taken together, our data suggest that for Spy, the optimal folding surface uses a heterogeneous mixture of hydrophobic patches to bind aggregation-prone surfaces,⁹ and charges to relieve repulsive interactions between negatively charged residues within the substrate that may inhibit folding. Given that Spy can bind to both folded and unfolded Im7 conformations,¹³ in which different chemical compositions of amino acids would be presented to the chaperone, such a heterogeneous surface is likely an essential feature of Spy's chaperone function.

We also investigated if different regions of Spy prefer binding either unfolded or helical parts of Im7_6–45 (Figure 3B and Supporting Methods, and Figure S10). Interestingly, the center of the cradle of Spy more favorably interacts with unfolded parts of the substrate, while the rim of the cradle exhibits a weaker selectivity toward helical and unfolded Im7_6–45 residues. Notably, His96 and Gln100 show a strong propensity to interact with unstructured regions of the substrate (Figure S10). This observation helps to explain why during genetic selections to enhance chaperone activity these two residues were mutated to leucines,⁹ as the placement of hydrophobic residues at these sites may improve Spy's ability to interact with exposed hydrophobic residues in unfolded regions of the substrate. This hypothesis is also consistent with our recent findings that these two mutations increase the hydrophobicity of Spy:Im7 binding, and that the unfolded state of Im7 binding to Spy is more mediated by hydrophobic interactions than for the native state.¹² This observation suggests that the cradle of Spy provides a protected environment for its substrate, where initiation of the substrate folding would occur. While the substrate folds, it may progressively move toward the rim of Spy.

Conformational Dynamics of Spy Upon Binding

In independent experiments, we also solved the co-ensemble of Spy bound to Im7_6–45 by X-ray crystallography.¹¹ From this crystallographic ensemble, two significant structural differences were evident in Im7-bound Spy relative to apo Spy. First, the Im7-bound Spy dimer is twisted about its center relative to substrate-free Spy. Second, residues 47–57, which in apo Spy are relatively flexible as indicated by high B factors, became even more disordered in bound Spy, to the extent that the electron density of this segment becomes too disordered to be resolved. This disorder indicates that this segment takes on multiple conformations when Spy is bound to Im7.

To examine whether similar changes in Spy occur in solution upon association with Im7_6–45, we compared the global and local dynamics of apo and bound Spy in our simulations (Figure 4). We measured global conformational changes by defining a pseudo-dihedral angle and an interdomain distance that describe the relative position of the two Spy monomers (Figure 4B and Supporting Methods). Free energy surfaces projected onto this two-dimensional subspace reveal a single, broad free energy minimum for both apo and bound Spy in the simulations, with a small diminution of the breadth of this minimum for the bound state. This observation indicates that Spy retains most of its conformational plasticity while interacting with its substrate (Figure 4A). Interestingly, we observe a−4.6° twist in Spy upon binding to substrate (Figure 4A and Table 1). This twist is similar to the −9° twist observed in the bound crystal structure. It could be that this twist in Spy helps to provide greater heterogeneity for Im7 binding and folding.

Figure 4.

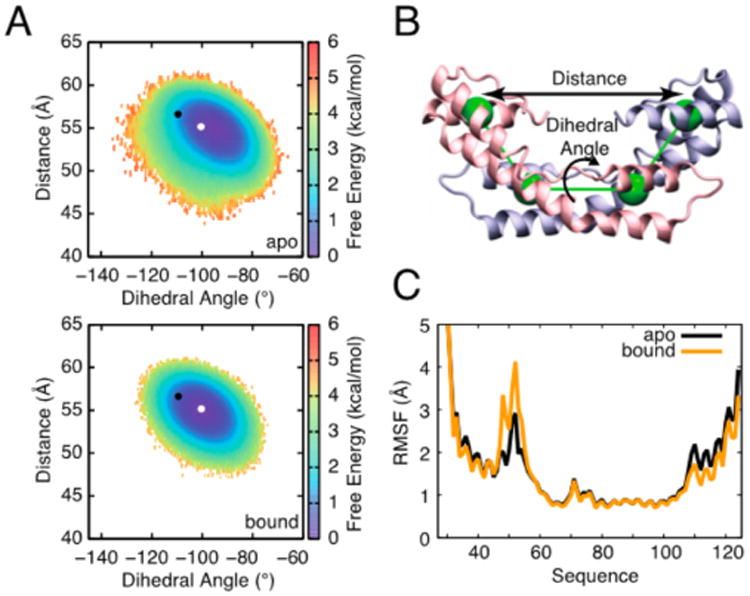
Comparison of Spy conformational dynamics in its free and bound states. (A) Free energy landscapes constructed along two parameters describing the relative position of the two Spy monomers: an interdomain distance and dihedral angle, as illustrated in panel (B). On the free energy surfaces, the white and black points, respectively, indicate the coordinates of the Spy dimer in the apo (−100.4°, 55.2 Å) (top) and bound (−109.4°, 56.6 Å) crystal structures (bottom). Conformational sampling during the bound simulations shifts toward the coordinates of the bound Spy crystal structure: the average coordinates for the apo and bound simulations are (−95.6 ± 0.2°, 54.7 ± 0.1 Å) and (−100.2 ± 0.2°, 54.9 ± 0.1 Å), respectively. A small decrease in intermonomer dynamics is also observed upon binding. The color bars denote the free energy in kcal/mol computed at 300 K. (C) The root-mean-square fluctuations (RMSFs) of residue Cα positions during coarse-grained simulations of apo Spy (black) and bound Spy (orange). While residues near the N and C termini show decreased dynamics in the bound state, the flexibility of the disordered linker region (residues 47–57), which is important for interacting with Im7_6–45, notably increases. A block error analysis of the in RMSF values indicates that the differences observed in the loop region are significant (Figure S11).

Analysis of local, per-residue fluctuations reveals that upon binding, dynamics are diminished near the N and C termini. Meanwhile, the dynamics of the flexible loop region are predicted by our model to notably increase (Figures 4C and S11), in agreement with the loops being unresolved only in the substrate-bound crystal structure of Spy¹¹ (Table 1) and possibly allowing for better interaction with the various conformations of Im7_6–45. This observation suggests a mechanism of molecular recognition in which a redistribution of the conformational dynamics⁶⁴ occurs in a way that maximizes the chaperone's capacity to interact with its partner,^40,44 underscoring the importance of disorder in chaperone function.¹⁰

Spy Stabilizes More Folded Conformations of Im7

To investigate further how Spy can interact with its substrate, a conformational network analysis was performed on our Spy–Im7_6–45 binding simulations^65,66 (Figure 5). In this approach, we first clustered the conformational ensemble of Im7_6–45 from simulation into groups, or substates, that exhibit similar structural features (Figure 5A). The structural similarity between two conformations was assessed based on the networks of inter-residue contacts present in both conformations (Methods). For apo Im7_6–45, 11 substates were detected, which range from compact, largely folded conformations (e.g., substate 3 or 11), to extended, largely unstructured conformations (e.g., substate 2 or 8) (Figure S12). This network of substates was also used to investigate the conformational behavior of Im7_6–45 while interacting with Spy (Figure 5A). The changes in the energy landscape of Im7_6–45 upon interaction with Spy can be described by the reweighting of the population of these different substates (Figure 5B). Clearly, bound conformations are biased toward substate 3, which is highly folded, and substate 6, which is characterized by a folded N-terminal helix and an unfolded C-terminus (Figure S12). The two most dominant substates in unbound Im7_6–45 (1 and 2), which both exhibit a small degree of residual structure (Figure S12), become lowly populated (<5%) in the Spy-bound environment. It is worth noting that substates 3 and 6 are the most compact conformations (Figure S13), indicating that a compaction of Im7_6–45 occurs while bound that may improve its capacity to interact with Spy.

Figure 5.

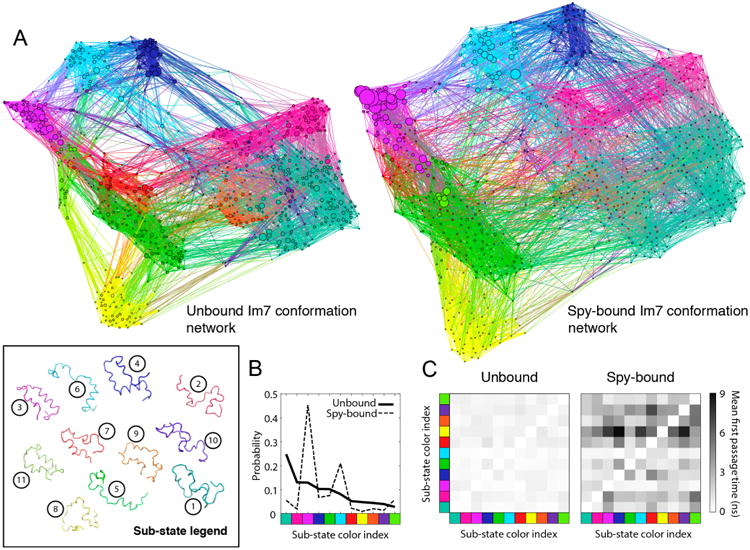
Network and kinetic analysis of Spy–Im7_6–45 simulations. (A) Conformation-space networks are shown for the unbound and bound ensembles of Im7_6–45. The nodes in each network correspond to a particular Im7_6–45 conformation, and the links between nodes indicate a transition between conformations during simulation. Node size is proportional to the population of a conformation in the ensemble, and the colors denote the substate to which a conformation belongs. The box at the bottom left shows a representative conformation for each of the substates, which are displayed using the same colors as in the networks. The numbers adjacent to each conformation show the index for each substate. (B) Populations of each substate in the bound and unbound ensembles. The indices for the substates are chosen as a ranking for the population in the unbound ensemble: substate 1 has the highest weight and substate 11 has the lowest. Reweighting of the substate population indicates that Im7_6–45 gains structure upon binding Spy. The axes labels show the color index of the substates, which are ordered according to their indices. (C) The mean first passage time for transitions between substates is shown using a heat map, with black indicating a slow transition and white indicating a fast transition. These data indicate that transitions between different Im7_6–45 substates are slowed down when bound to Spy.

These observations from the binding simulations are consistent with our previous genetic, structural, and kinetic evidence that Spy directly assists in the folding of proteins^8,9,11,13 (Table 1). Most importantly, they provide a new perspective on the challenging question of how a chaperone protein can assist in the proper folding of its substrates.

Spy Slows Down Conformational Transitions of Im7

To determine if the interaction with Spy also affects the speed at which Im7_6–45 can transit between different substates, we calculated the average time necessary to observe a transition between any pair of substates in the simulations.⁶⁵ Such “mean first passage times” were determined for free and bound Im7_6–45. Spy binding was found to slow down the vast majority of substate-to-substate transitions (Methods and Figure 5C). Accordingly, using substates 3 and 1 to define the folded and unfolded states, respectively, of the Im7_6–45 substrate, we observe in the simulation that binding to Spy slows down the kinetics of both substrate folding (by a factor of 2) and substrate unfolding (by a factor of 5), but that these transitions still occur while continuously bound to Spy. This trend is similar to the slowdown of folding and unfolding experimentally observed during stopped-flow kinetic measurements of full-length Im7 upon Spy binding¹³ (Table 1), suggesting that the coarse-grained model, despite its simplicity, captures the qualitative kinetic changes that occur in full-length Im7 upon binding.

Spy–Substrate Binding Pathway

To understand how Spy captures and releases Im7, we also characterized the chaperone–substrate interaction mechanism from our optimized simulations. Figure 6 shows a two-dimensional free energy surface that describes the binding and release mechanism of Im7_6–45 while it folds. Consistent with the substate analysis above, Spy binding shifts the conformational equilibrium of the Im7_6–45 substrate toward more-folded substates (the B_F basin). Far from Spy, Im7_6–45 mainly undergoes exchange between a largely folded (F) and an unfolded state (U), consistent with our relaxation data on free Im7_6–45 (Figure S3). The binding pathway proceeds through both unfolded and folded nonspecific complexes (NS_F and NS_U), fully consistent with recent kinetic and thermodynamic measurements.^12,13 The energy barriers to transit from bound and folded Im7_6–45 (B_F) to unbound and folded Im7_6–45 (F) is about 5 kcal/mol while the transition from B_F to unbound and unfolded Im7_6–45 (U) is higher (about 7.5 kcal/mol), suggesting that Spy tends to release Im7_6–45 into its folded state. Very recently, we found that Spy releases folded Im7 faster than unfolded Im7,¹² providing corroborating evidence from kinetic measurements for this observation. Notably, Spy–Im7_6–45 binding simulations performed with the unoptimized force field yield a different interaction mechanism that is less consistent with available kinetic,¹³ thermodynamic¹² and X-ray¹¹ data (Figure S14).

Figure 6.

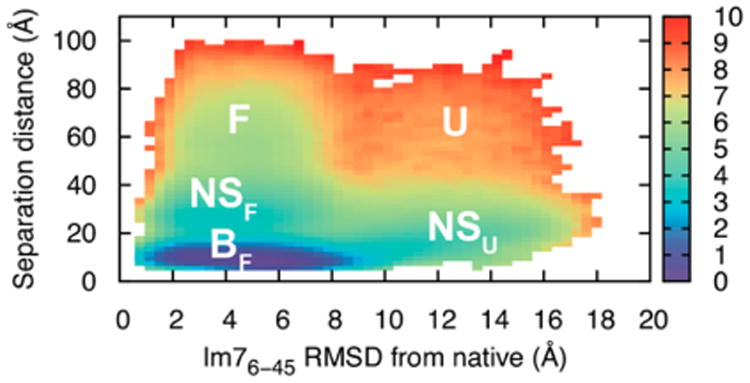
Spy–Im7_6–45 binding mechanism. A free energy surface of the Spy–Im7_6–45 separation distance and the Cα-RMSD of Im7_6–45 to the equivalent segment in the crystal structure of full-length, native-state Im7. The separation distance is defined as the distance between the centers of mass of Spy and Im7_6–45. The labels signify different conformational states of the Im7_6–45 substrate in the presence of the Spy chaperone: B_F (bound and largely folded), NS_F (nonspecific complex and folded), NS_U (nonspecific complex and unfolded), F (unbound and well-folded), and U (unbound and unfolded). The surface is computed at the simulation temperature of 300 K and the colorbar denotes the free energy in units of kcal/mol. The free energy is normalized by the volume of a spherical shell with a radius corresponding to a given distance.

Conclusions

In this study, we combine site-specific NMR measurements with coarse-grained molecular dynamics simulations to investigate a heterogeneous, dynamic chaperone–substrate interaction. We construct a system-specific force field using easily accessible NMR data on individual binding components. We then use this model in coarse-grained binding simulations to obtain a description of a flexible protein–protein complex at single residue-level resolution. Our results are highly congruent with several independent sources of biophysical data, thereby validating our approach. By investigating the interaction between the chaperone Spy and its substrate Im7, we found that Im7 binds within the interior of Spy's cradle in a flexible ensemble of partially folded states that can interconvert while continuously bound to the chaperone surface. Our results reveal specific information about how Spy and Im7 mutually modify their respective conformations and dynamics, substantially improving our understanding of chaperone-facilitated protein folding. For the chaperone Spy, the linker region becomes more flexible in the bound form, which appears to offset losses in dynamics elsewhere in the chaperone and to improve the interaction with multiple conformations of the Im7 substrate. With respect to the Im7 substrate, its energy landscape is modified upon chaperone binding through a shift toward more-folded conformers and a slowdown in the conversion between different partially folded states. Thus, a redistribution of conformational flexibility is observed upon binding both within the chaperone and between the chaperone and its substrate. As Spy is an ATP-independent chaperone, this possibility of redistribution in conformational flexibility might allow the substrate to transition along its folding pathway in the absence of external energy sources.

Understanding interactions between flexible proteins remains an important challenge. Unfortunately, it is often difficult to obtain high-resolution X-ray co-structures or an atomic resolution description from NMR for flexible complexes. Here, we show that by constructing system-specific force fields using the individual structures of the two components, their NMR chemical shifts, and the binding affinity of the complex, one can obtain a realistic description of a highly flexible complex. The realistic nature of this description is confirmed by the high correspondence of our model to several biophysical measurements and tests with two well-studied model systems. One of the advantages of our approach is that it only requires three sources of experimental data, which for many interesting systems have already been obtained: structural models of the two individual components, assigned NMR spectra, and a binding affinity for their interaction. Thus, we expect that our approach will be generally useful in examining the structure and dynamics of binding for many systems.

Methods

NMR Spectroscopy

All NMR experiments were recorded on 600 or 800 MHz Varian spectrometers equipped with a triple-resonance cryo-probe with pulse field gradient. All spectra were processed using NMRPipe⁶⁷ and analyzed using Sparky.⁶⁸

Protein Assignment

HNCO, HNCA, HN(CA)CO, HN(CO)-CA, CBCA(CO)NH, and HNCACB tridimensional experiments were recorded for both Spy and Im7_6–45 to assign HN, N, CO, CA, and CB of the two proteins.⁴⁷ For Im7_6–45, two sets of experiments were run under low- and high-salt conditions at 298 K; for Spy, the assignment was performed at 313 K and transferred at 298 K using ¹⁵N heteronuclear single quantum coherence (HSQC) recorded at various temperatures. The assignment of the spin system was realized in a semi-automated fashion using the program MARS.⁶⁹ An additional ¹⁵N-HSQC-NOESY with a mixing time of 100 ms was recorded for Spy to confirm the assignment. PANAV was used to further validate the obtained assignments.⁷⁰ The chemical shifts of Spy and Im7_6–45 are deposited in the BMRB under the access codes 26849 and 26850, respectively.

Spin Relaxation

¹⁵N spin relaxation measurements were performed using standard experiments allowing for the measurements of R₁, R₂, and {¹H}-¹⁵N NOE.^50,51 The times used to sample the magnetization decay were 0, 100, 200, 400, 600 (twice), 800, 1100, 1500, and 1900 ms for longitudinal relaxation and 10, 30, 50, 70 (twice), 90, 130, 170, 210, and 250 ms for transverse relaxation. For the measurement of the NOE, long recycling delays, above 8 s, were used and saturation of the amide proton was achieved using a WALTZ16 scheme for 3 s. The FUDA package was used to fit the different resonances and extract relaxation rates. Model-free analysis of Spy was achieved using the software TENSOR2,^55,56 and the crystal structure PDB ID: 3O39 was used as a structural model.⁸ The analysis was restricted to residues where all three relaxation rates could be accurately measured.

Molecular Modeling

All molecular simulations were performed using CHARMM⁷¹ and are based upon Gō models originally constructed using the Multiscale Modeling Tools for Structural Biology Gō model server.⁷² The simulations were carried out as follows.

For the coarse-grained simulations of Spy and Im7_6–45 alone, we implemented a Gō-like model that takes into account sequence effects.⁴⁵ In this model, each residue is represented by a single bead located at the Cα position, and attractive interactions are defined between residue pairs that are close together in the experimental structure, as described previously.^42,45

Initial Parametrization

An initial model for the substrate was taken from residues 6–45 of the crystal structure of full-length Im7 (PDB ID: 1CEI).⁴⁹ To capture the unfolded nature of Im7_6–45, we applied a dihedral adjustment to the torsion angle potential to help alleviate an α-helical bias in the model⁴¹ and then used the force field optimization procedure outlined below to renormalize the strength of native contacts in the model such that the per-residue helical propensity in simulation matched that from experiment. For each round of the optimization, 100 independent 1.5-μs-long trajectories of Im7_6–45 were run, which has been shown to be an appropriate aggregate simulation length for calibrating the Gō-like model to study unfolded proteins.⁵⁸

Initial coordinates for the Spy chaperone were obtained from the apo crystal structure (PDB: 3O39).⁸ The modified torsion angle potential was used and inter- and intramolecular interactions in Spy were uniformly scaled by a factor of 1.3 to maintain the dimer interface while still permitting significant flexibility within the monomers. This approach yielded a good agreement between calculated and experimental chemical shifts (Figure S5B and Table S5). A total of 100 independent 375 ns-long simulations of Spy were performed.

Force Field Optimization and Final Trajectory

Using the initial force field for Im7_6–45, a helicity profile was obtained as the average of the 100 1.5 μs simulations. N = 1000 equally spaced conformers were extracted and the local helicity for residue l in conformer k, F_k,l was determined using the software PCASSO⁷³ to be either 0 for non-helical or 1 for helical. For each residue l, the calculated helicity value was obtained as

$$F_l^{\text{calc}}=\sum _{k=1}^N{p}_k{F}_{k,l}$$

where p_k is the weight of conformer k (equal to 1/N in this initial run). The sequence was divided in six segments chosen by starting a new segment every time the sign of the difference between the experimental and predicted helicity profile changed. The native potential, composed of 88 interatomic interactions (or native contacts) between residues i and j, characterized by the scaling factor ${\varepsilon }_{ij}^0$, was adjusted by introducing a single optimized scaling factor, λ_i, for all of the residues within each segment, providing a new interaction parameter according to

$${\varepsilon }_{ij}={\lambda }_{ij}{\varepsilon }_{ij}^0$$

where

$${\lambda }_{ij}=\sqrt{{\lambda }_i{\lambda }_j}$$

For the initial simulations, λ_i was set to 1 for all segments. The optimization is done in an iterative manner in which the N conformers extracted from the previous sampling are subject to a reweighting according to⁴⁶

$$p_k^{\text{new}}=p_k^{\text{old}}\frac{{\mathrm{e}}^{-V_k^{\text{new}}/k_{\mathrm{B}}T}}{{\mathrm{e}}^{-V_k^{\text{old}}/k_{\mathrm{B}}T}}$$

where $p_k^{\text{new}}$ and $p_k^{\text{old}}$ are the relative weights, $V_k^{\text{new}}$ and $V_k^{\text{old}}$ are the potential energies of the conformer k in the new and old force field, k_B is the Boltzmann constant, and T is the temperature of the simulation. The optimization procedure is realized in a way to minimize the following cost function:

$${\chi }^2=\sum _{l=1}^M{(F_l^{\text{calc}}-F_l^{exp})}^2+N\sum _{k=1}^N{(p_k^{\text{new}}-p_k^{\text{old}})}^2$$

where M is the number of residues, $F_l^{\text{new}}$ is the fraction of helicity of residue l as derived from the SSP analysis of the ¹³C chemical shifts, and $F_l^{\text{calc}}$ is the fraction of helicity of residue l computed as the population weighted average over the N conformers in the ensemble. The second term, which corresponds to a weak restraint on the weight change of each conformer, was introduced to avoid excessive reweighting of a particular conformation, which could induce unwanted perturbation of the force field.⁵³ The procedure was iterated six times to reach convergence and the desired agreement with the experimental data. No further improvement was observed by pursuing the optimization with an additional iteration. The use of an iterative procedure where the reweighting of each conformer is kept reasonable allows for a smoother evolution of the force field parameters, therefore avoiding the introduction of major, potentially problematic, distortion of the force field parameter space.

High-Salt Case

For studying the high-salt case, a similar procedure was used to optimize α, a parameter that scales all the interactions involving at least one charged residue. The effect of α on the force constants is

$${\varepsilon }_{ij}^{\text{high}-\text{salt}}={\alpha }_{ij}{\varepsilon }_{ij}^{\text{low}-\text{salt}}$$

with

$${\alpha }_{ij}=\{\begin{array}{cc}1& \text{if both}i\text{and}j\text{are uncharged}\\ \sqrt{\alpha }& \text{if one of}i\text{and}j\text{is charged}\\ \alpha & \text{if both}i\text{and}j\text{are charged}\end{array}$$

A single step of optimization was used for determining the optimal value of α = 1.2. Note that a value of α larger than 1.0 corresponds to an increase in the strength of the interactions involving charged residues, amounting to the screening of repulsive interactions due to an increase in ionic strength.

Binding Simulations

To simulate chaperone–substrate interaction, we incorporated a generic Cα-based interprotein potential alongside the Gō-like model. All possible Spy–Im7_6–45 intermolecular residue pairs interact through a standard Lennard-Jones potential. For this potential, the interaction radii were obtained from a survey of the Protein Data Bank that determined the mean intermolecular Cα–Cα distance for each amino acid pair.⁷⁴ Residue-pair-specific interaction strengths were scaled in proportion to the Miyazawa–Jernigan statistical contact energies.⁷⁵ We tuned the interprotein potential by uniformly scaling the interaction strengths with an efficient reweighting procedure⁵⁸ such that the calculated (0.11 μM) and experimental (0.14 μM) binding affinities are in good agreement. The binding affinity is therefore the only experimental information on the complex that we used to calibrate the force field for the binding simulations. Ten independent 6 μs long binding simulations were performed. We ran an additional set of 10 binding simulations that yielded essentially the same results (0.12 μM binding affinity and an R value of 0.99 for the interprotein contact maps).

Network Analysis

Im7_6–45 conformations in the trajectories alone or in interaction with Spy were clustered together into 700 discrete groups using MSMBuilder.⁷⁶ Clustering was performed using the same set of contacts that are defined in the Gō-like model and a cutoff of 8 Å to form Boolean vectors for each frame. The distance metric used for clustering was the distance between these Boolean vectors. In the free trajectories, all Im7_6–45 conformations were labeled “unbound”. In the presence of Spy, a frame was considered bound if any atom in Im7_6–45 was less than 8 Å away from any atom in Spy, and unbound otherwise. Thus, two different environments were defined (“unbound” and “bound”), and a separate transition matrix for each was calculated to obtain environment-specific populations for all 700 groups in the network. This information was used to create environment-specific network plots in the program Gephi,⁷⁷ following previous work.⁶⁵ These were clustered into so-called “substates” using a modularity optimization algorithm, which maximizes connections within a given substate and minimizes connections between different substates.⁷⁸ The substates were shown using colors in the network plots.

Kinetic Analysis

Once the trajectories are clustered, and the clusters further grouped into substates, it becomes possible to compute the average time for transition between the 11 substates for the two environments defined above. These average times were computed using an algorithm described previously,^65,66 with an additional criterion that the trajectory must remain in the environment for the duration of the transition. Restated, the average transition time from, for example, substate 1 to substate 2 in the “bound” environment was computed using trajectory segments that remain bound throughout the transition.

Supplementary Material

supplemental

Supporting Methods section, Figures S1–S19, and Tables S1–S5, including NMR spectra and relaxation properties of Im7_6–45 and Spy, model building for Spy, additional comparison of interaction pattern to biophysical data, CD spectroscopy, structural properties of Im7_6–45 substates, convergence of optimization, and test of the approach on known complexes (PDF)