Biomechanics as a window into the neural control of movement

Abstract

Biomechanics and motor control are discussed as parts of a more general science, physics of living systems. Major problems of biomechanics deal with exact definition of variables and their experimental measurement. In motor control, major problems are associated with formulating currently unknown laws of nature specific for movements by biological objects. Mechanics-based hypotheses in motor control, such as those originating from notions of a generalized motor program and internal models, are non-physical. The famous problem of motor redundancy is wrongly formulated; it has to be replaced by the principle of abundance, which does not pose computational problems for the central nervous system. Biomechanical methods play a central role in motor control studies. This is illustrated with studies with the reconstruction of hypothetical control variables and those exploring motor synergies within the framework of the uncontrolled manifold hypothesis. Biomechanics and motor control have to merge into physics of living systems, and the earlier this process starts the better.

Physics of living systems

Movement science is a very broad and diverse field. I would like to focus here on two components of movement science that, in my opinion, have more similarities than differences. The two components, biomechanics and motor control, have traditionally been separated in both teaching programs and professional meetings. There are courses in biomechanics and motor control (sometimes also addressed as neural control of movement or movement neuroscience), biomechanics conferences with minimal representation of motor control researchers and motor control conferences with only a handful of biomechanists in attendance. This is puzzling because the two areas share a core attitude to biological movement: they are both parts of natural science, physics of living systems.

Physics of inanimate nature is a mature science with an impressive computational apparatus. It succeeds in uniting our experiences into a handful of basic laws. These laws, however, demonstrate striking inability to describe behavior of biological objects. Imagine an insect and a toy that is a perfect copy of the insect according to all its mechanical characteristics. If you leave the insect and the toy on the kitchen table and return a few hours later, most likely the toy will stay where you left it while the insect will be gone. The reason for the difference in the movements of the toy and the insect is the fact that the insect is an active system, which does not violate laws of mechanics, but is able to tweak them to its advantage. Later we are going to discuss what “tweaking” means in this context. Activity as a salient feature of biological systems was appreciated by Bernstein who spent the last years of his life trying to develop physiology of activity (Bernstein 1966, 1967). To me, physiology of activity is synonymous with physics of living systems.

I am going to assume that biological systems obey natural laws that rule the inanimate world as well as currently unknown laws specific for active systems. So, the challenge of motor control is to discover those unknown rules, and biomechanics is one of the cornerstones of this endeavor. On the one hand, knowledge of biomechanics is crucial to be able to take into consideration the contribution of mechanical interactions to observable movement patterns. On the other hand, many experimental approaches to motor control problems involve analysis of mechanical variables. In fact, there is no clear border between the two. Consider, for example, studies of reflex effects on mechanical properties of effectors or the neural coordination of joint trajectories or the effects of a neurological injury on the patterns of digit forces in prehensile tasks. All these belong equally to both biomechanics and motor control.

Challenges of biomechanics

Applications of classical mechanics to human and animal movements date back to the classical works of Borelli. At those times, mechanical analysis of the human body was commonly combined with functional anatomy and limited primarily to studies of cadavers. The emergence of new methods of movement analysis in the nineteenth century, in particular filming moving people and animals by Marey and Myubridge, signified an important step to mechanical analysis of natural voluntary movements (reviewed in Cappozzo et al., 1992). Since those times, it has become clear that development of biomechanics is crucially dependent on methods of accurate measurement and exact definitions of salient variables and parameters. These challenges persist in our times. I would like to suggest that the reader tries to define such commonly used terms in biomechanics as “joint torque” and “muscle work” (the definitions should be applicable across conditions, e.g., isotonic and isometric). After you write down your definitions, check them against the relevant Chapters in a recent book (Latash and Zatsiorsky, 2016).

Writing equations of classical mechanics for moving objects, including parts of the body of a moving animal, is not problematic. The problem is in adequacy of those equations for analysis of biological (active!) systems. Frequently, analysis of moving effectors, from a single muscle to the whole body, is performed using linear models representing combinations of inertial, elastic and damping terms:

$$F_M=-F_{EXT}+m{\text{d}}^{2}x/\text{d}{t}^2+\text{bd}x/\text{d}t+k(x-x_0)$$ (1)

where F_M is muscle force, F_EXT is external force, x is coordinate, t is time, x0, m, k and b are parameters, commonly assumed to be constants. Such equations are sometimes able to fit experimental data well. However, one should not forget the goal of any research in physics (and mechanics): to understand the origins of observed behaviors, not to fit experimental curves with high accuracy. In order to reach those goals, one has to make sure that the coefficients in the equations have clearly defined physical meaning and that the functional form of the equation is adequate. Both issues are challenging.

While the coefficients in Eq. (1) look like mass, damping, stiffness and resting length of a spring, they may become meaningless if the equation is applied to an object, which does not behave as a second-order linear system. For example, studies of the same human joints reported damping and stiffness coefficients that could differ from each other by two orders of magnitude (reviewed in Latash and Zatsiorsky, 1993; Zatsiorsky, 1997). Some studies even reported negative stiffness coefficients (Dyhre-Poulsen et al., 1991), which is clearly meaningless. Imagine that you are stretching a muscle very slowly and at some point, the muscle force along the direction of stretch starts to drop with further elongation (which represents typical muscle behavior, see chapters in Herzog, 2000). Formally, if one computes the partial derivative of force with respect to the coordinate, one gets a negative value of muscle stiffness. The only conclusion from this result, however, is not that the muscle can have negative stiffness, but that the muscle is not a spring and the notion of stiffness cannot be applied (for more detailed discussion and alternative terminology see Latash and Zatsiorsky, 1993, 2016).

Even if Eq. (1) were adequate (which it is not!) or if we knew a different, truly adequate equation, defining its coefficients would not be easy. Indeed, even mass-inertial properties of moving effectors change due to changes in the blood flow and geometry of the muscles and other tissues with muscle contraction. Using traditional system identification techniques to compute parameters in such equations is likely to lead to unreliable, or even physically impossible, results. Such methods certainly imply that parameters of equations stay constant while the system of interest responds to an external perturbation (e.g., a quick change in the external force). However, this is not true for active systems. For example, a perturbation applied to an effector leads, at a short time delay, to changes in muscle activations due to reflex loops. As a result, the coefficients in Eq. (1) analogous to stiffness and damping change rather dramatically (for reviews see Winters and Crago, 2000). If one analyzes the response of a system to a perturbation over a very short time interval, shorter than the quickest reflex latency (e.g., Bennett et al., 1992), two issues emerge. First, the salient coefficients may still change with a change in the system geometry. Second, the computed coefficients will have little relevance to natural behavior of the system because, effectively, one would study the response of a deafferented effector. In other words, one always deals with a dynamic (time-varying) system with changing coefficients. Clearly, Eq. (1) (and similar equations) cannot provide an adequate representation of such systems.

I hope that the previous few paragraphs have convinced the reader that biomechanics is a very non-trivial extension of classical mechanics to objects that differ rather dramatically from objects in the inanimate nature. This makes biomechanics a very exciting field: mechanics of objects that evade direct observation and change their properties in the process of experimental analysis.

Challenges of motor control

Motor control deals with both known and unknown laws of physics. On the one hand, living systems do not violate any laws of nature. On the other hand, as emphasized in the opening section, they are active: this means that behavior of a living object cannot be predicted given its initial state (at least given our current ability to specify such a state) and external forces. Indeed, natural inanimate objects do not roll uphill, swim against the current and fly against the wind, while animals have little problems with such tasks and behaviors.

I see the main challenges of motor control in the formulation of unknown laws of nature that define active movements performed by living systems. Of course, these unknown laws have to be based on basic laws of physics, but the complexity of the structure of and interactions within a living system (starting from a single cell or even a macromolecule) leads to unpredictable behaviors. Sometimes such behaviors seem to violate some of the basic laws of physics, e.g., moving away from a state with minimal potential energy as in hiking uphill. As written in one of my favorite books, Murphy’s Law (Bloch, 2003): “Under the most rigorously controlled conditions of pressure, temperature, volume, humidity and other variables, the organism will do as it well damn pleases” (Harvard’s Law).

Clearly, if there are problems in the application of the apparatus of classical mechanics to biological movement, such problems become much worse when one tries to study the neural control of such movements. While approaches based on control theory have been used to describe the neural control of movement, these approaches are by definition non-physical. They were developed to describe the control of human-made inanimate objects such as ballistic missiles equipped with powerful actuators and signal transmission circuits with close to zero time delays. Application of these methods to problems of motor control assumes computational processes within the body (cf. “computational neuroscience” – an oxymoron in my opinion). Such approaches are equivalent to assuming that electrons measure each other’s charge and distances between them to compute the requisite forces and then send signals to actuators to implement the results of such computations. While the last phrase is ridiculous, I see no major difference between it and assumptions that some neural structures in the brain compute forces needed to produce desired movements and then send signals to muscles to implement those forces (see Latash, 2010).

Motor control studies use a variety of tools, such as electromyography (EMG), brain imaging, electrical stimulation of excitable structures and – of course! – analysis of movement mechanics. As discussed in the next sections, studies of movement mechanics provide crucial information for theories in the field of motor control. On the other hand, they also lead sometimes to hypotheses incompatible with the known physiology of the human body; I am going to address such approaches as “mechanical reductionism” (see Feldman, 2015).

Mechanics-based hypotheses in motor control

A number of motor control hypotheses have been based on assumptions that the CNS computes neural signals corresponding to desired mechanics of planned movements. These approaches originate from the notion of a generalized motor program (Schmidt, 1975), which assumed that neural variables were stored in memory encoding patterns of mechanical variables (such as forces and torques) that could be scaled by time and amplitude to generate slower-faster and weaker-stronger actions. More recently, these approaches have been formalized as the control of movements with the help of internal models, neural processes simulating or computing interactions both within the body and between the body and the environment (reviewed in Wolpert et al., 1998; Kawato, 1999; Shadmehr and Wise, 2005). As applied to the neural control of movement, inverse models are assumed to compute neural signals based on desired mechanics, while direct models are assumed to compute expected mechanical outcomes of the ongoing neural processes; both types of models are combined to control natural actions. Much of the experimental support for the idea of internal models comes from experiments with adaptation to unusual force fields and after-effects of such adaptations (Shadmehr and Mussa-Ivaldi, 1994; Ostry and Feldman, 2003; Shadmehr and Wise, 2005).

The idea of motor programming and internal models is indeed based on mechanics. Consider how a person produces a movement of a hand to a new location in space. To move a motionless object, a pattern of force has to be applied to that object. Given the anatomy of the arm, moments of force in individual joints have to be generated to produce the desired force profile acting on the hand. These moments of force have to be produced by muscles crossing the joints taking into account motion-dependent torques, including joint interaction torques. Muscles have to be activated to produce forces. Muscle activation depends on descending and reflex inputs into the corresponding motoneuronal pools. And so on. The first few of the mentioned steps belong to the realm of mechanics. Most of them require solving problems with more variables than constraints (problems of motor redundancy, Bernstein, 1967). But in general, they can be solved assuming some additional criteria, for example minimization of a cost function.

A variety of optimization criteria based directly or indirectly on mechanical variables have been used in motor control. The minimum-jerk criterion (Hogan, 1984; Flash and Hogan, 1985) is arguably the most commonly used cost function in studies of movement kinematics. According to this criterion, a trajectory is selected that minimizes the integral over movement time (MT) of the third time derivative of the coordinate (jerk, J = d³x/dt³) squared:

$$J=\frac{1}{MT}{\int }_0^{MT}{(d^{3}x/d{t}^3)}^{2}dt$$ (1)

Application of this criterion leads to a solution in the form of a sixth-order polynomial function with the bell-shaped velocity profiles resembling ones seen in natural movements. There was an attempt to extend the minimum-jerk criterion to kinetic variables: the minimum-torque-change model (Uno et al., 1989):

$$\begin{array}{l}\\ \\ C=\frac{1}{MT}{\displaystyle {\int }_0^{MT}{(dT/dt)}^{2}dt}\end{array}$$ (2)

where C is the cost function and T is torque. For a purely inertial one-element system the criteria (1) and (2) produce identical results because rotational acceleration is proportional to torque. Both the minimum-jerk and the minimum-torque-change criteria fail, however, when movements of multi-joint systems are considered.

Physiological optimization criteria have been commonly based on mechanical variables. For example, the problem of sharing force among multiple muscles has been addressed as that of minimization of fatigue. Endurance time (T_E), time during which a muscle can produce a certain force level, is related to muscle stress, that is, the ratio of force to the physiological cross-sectional area (F/PCSA): T_E = (F/PCSA)^–3 (Crowninshield and Brand, 1981). The inverse of T_E may be defined as muscle fatigue, and the minimum fatigue criterion can be formulated using the following cost function:

$$\begin{array}{l}\\ C={{\displaystyle {\sum }_{i=1}^n(F_i/PCS{A}_i)}}^3\end{array}$$ (3)

where n stands for the number of muscles. Another physiological cost criterion is based on minimization of energy expenditure (Alexander, 2002):

$$\begin{array}{l}\\ C={\displaystyle {\sum }_{i=1}^n{\alpha }_i^p{F}_i^{\max }{V}_i^{\max }}\varphi (V_i/V_i^{\max })\end{array}$$ (4)

where function ϕ determines the metabolic cost; F_i^max and V_i^max are known maximum force and maximum velocity of each of the n muscles, respectively; V_i is instantaneous velocity of the i-th muscle; and is the unknown normalized activation of the i-th muscle, sought by minimizing the cost function C.

One of the problems with using optimization criteria has been the relatively arbitrary choice of cost functions based on intuition and personal views of the researchers. This problem has recently been partly overcome with the analytical inverse optimization (ANIO) method that allows computing cost functions for certain problems based on observations of behavior of the system of interest over a range of task constraints (Terekhov et al., 2010).

Typically, formal analysis of models based on the idea of programming mechanical variables starts and ends at the level of mechanics. In particular, the role of interaction torques during movements has attracted much attention. Problems with predicting and compensating for interaction torques have been invoked in studies of movements of patients with large-fiber peripheral neuropathy (“deafferented persons”, Sainburg et al., 1995) and in patients with cerebellar disorders (Bastian et al., 1996). Analysis of interaction torques forms the basis for the leading-joint hypothesis (Dounskaia, 2010). Among related approaches, one should mention the linear-torque-synergy idea proposed by Gottlieb and his group (Gottlieb et al., 1996); this idea assumes that torques during multi-joint movements represent scaled patterns of a single template.

It is obvious that the neural signals cannot be expressed in newtons and meters; the interactions among neurons are essentially electrical and the adequate physical units are volts. Appreciation of this fact led to a number of theories that presumed that the brain specified patterns of muscle activation adequate to produce desired mechanical effects. Arguably, the best-known examples are the dual-strategy hypothesis (Gottlieb et al., 1989) and the pulse-step model (Ghez and Gordon, 1987; Scheidt and Ghez, 2007).

These hypotheses, however, suffer from the same drawback as the force-control approaches: they assume that the brain structures encode time profiles of output variables, electrical or mechanical. This is clearly impossible for a dynamic system (cf. Glansdorff and Prigogine, 1971). To control such a system, one has to manipulate its parameters and output variables emerge given the actual conditions of movement execution, which are never 100% predictable.

The main problem of mechanical reductionism is ignoring the fact that the brain can only define parameters of physical laws, not variables linked by these laws. The only way to induce changes in output variables (e.g., displacements, forces, and muscle activations) is by changes in the parameters of the physical laws. To borrow an example from a recent book by Feldman (2015), consider a simple ideal pendulum consisting of a heavy ball connected by a rigid, weightless rod to a point of suspension (Figure 1). Motion of the ball is defined by the length of the rod, L, and the coordinates of the point of suspension, {x0, y0, z0} (assuming constant gravity). These are parameters of this simple system, and if one wants the pendulum to move differently in space and/or time, this person would have to modify those parameters.

Figure 1.

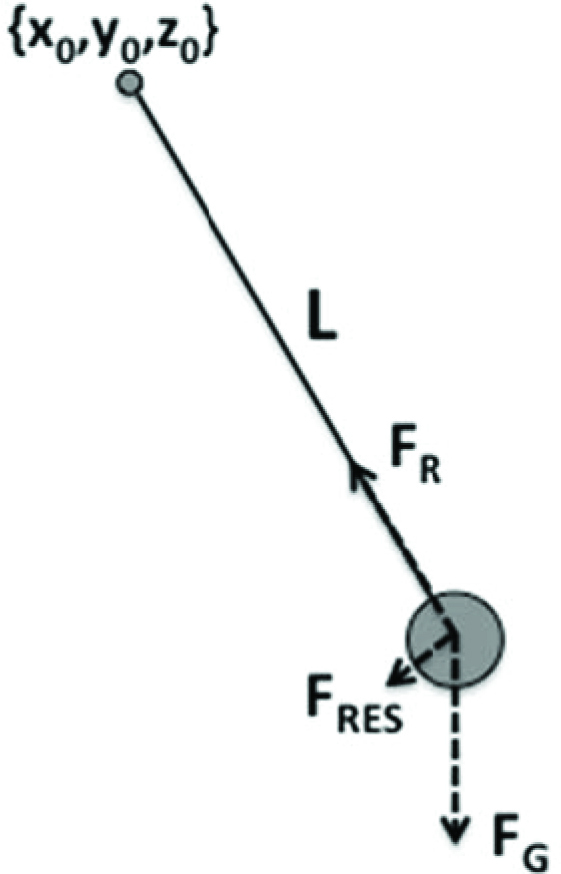
Parameters defining motion of an ideal pendulum include the length of the rod (L) and the coordinates of its suspension, {x0, y0, z0}. The forces emerge during the motion. FR – force applied to the ball by the rod; F_G – force of gravity; FRES – resultant force.

The ball motion is produced by changes in the forces acting on the ball from the rod (F_R) while the force of gravity (F_G) stays constant. These forces are not computed and implemented by actuators, however; they emerge given changes in the parameters. Of course, one could compute these force patterns and implement them with an actuator leading to the same ball motion (same resultant force, F_RES). This would be equivalent to simulating pendulum behavior with non-pendulum means. It can be done easily, but the meaning of such exercises escapes me. In more intuitive terms, driving a car does not require knowing or emulating the physical interactions translating effort applied to the steering wheel and to the gas/brake pedal to wheel rotation. One only has to be able to modify parameters of those physical interactions via action on the steering wheel and pedals, and this is sufficient to be a good driver (without being an expert in car engineering).

Is motor redundancy a problem?

Traditionally, motor redundancy has been viewed as a central problem in motor control. Indeed, Bernstein once coined a phrase “the essence of motor control is in the elimination of redundant degrees of freedom” (Bernstein, 1967). At any level of description of the system for movement production, there are more variables than constraints associated with typical actions. This problem has traditionally been analyzed at the level of mechanical variables. For example, how to compute joint rotations leading to a desired trajectory of the endpoint of a multi-joint effector? Or how to compute muscle forces leading to a desired value (pattern) of torque in a joint spanned by the muscles? Such problems emerge at non-mechanical levels as well. For example, how to select a specific pattern of recruitment of motoneurons to match a desired total level of muscle activation? Or how to compute individual synaptic inputs into a neuron to achieve a desired frequency of its firing? Such problems have no single solution. Most commonly, they have been approached using optimization methods (reviewed in Prilutsky and Zatsiorsky, 2002).

In fact, the formulation of the problem of motor redundancy, by itself, seems to be misleading. It assumes that the CNS cares about finding unique solutions to such problems and producing specific patterns of involvement of elemental variables. This assumption is another reflection of reductionism in motor control.

An alternative approach has been offered as the principle of abundance (Gelfand and Latash, 1998; Latash, 2012). This principle assumes that no single solutions are computed and implemented, but rather families of solutions can be observed that are all capable of performing the task. These families reflect not only the explicit task, but also desired stability of performance. A particular way of implementing the principle of abundance in the human body has been developed based on the ideas of hierarchical control, control with referent coordinates for salient variables and synergic control.

Arguably, the most famous, groundbreaking experiment in this area was performed by Bernstein in the 1920s (Bernstein, 1930). Bernstein constructed an ingenious device to record the kinematics of the arm during the repetitive movements of striking the chisel with the hammer. His subjects were professional blacksmiths who had performed this movement hundreds of times a day for years. So, if there is such a thing as an optimal joint rotation pattern for this motion, these subjects had it well learned. The main result of the study was that the tip of the hammer showed relatively low inter-trial variability while individual joints showed much higher inter-trial variability. Obviously, the brain could not send signals to the tip of the hammer, only to muscles that produced joint rotations. The result meant that: (1) No single optimal pattern of joint rotation was learned and reproduced; and (2) Joint rotations co-varied across trials to ensure relatively reproducible trajectory of the hammer. The second conclusion has direct relation to the notion of stability (cf. Schöner, 1995 and later in this paper).

How can a solution to this seeming problem be organized? Consider a hungry donkey and a person who wants the donkey to move to a new location. One method, suggested by the immortal Hodja Nasreddin, is to place a carrot in front of the donkey’s head and then move it to the desired location. Formally, this method means that a new referent location (carrot coordinate) is established for the donkey and the donkey’s head is moved by the difference between the referent and actual coordinates. Note that this method of controlling donkey’s movements seemingly involves solving multiple problems of motor redundancy since the donkey will have to move its legs, joints and muscles. The controller, however, does not worry about all these problems and relies on the general new law of donkey physics: donkeys move to carrots. Specifying a coordinate for the carrot parametrizes this law and a desired motion takes place, likely with varying movements of the legs, joints and muscles across repetitive trials.

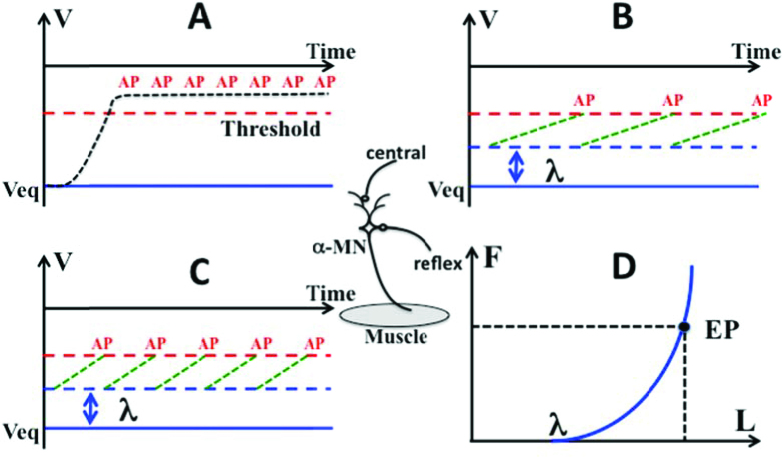
The basic principle of control with referent coordinates has to be linked to physiology. To appreciate how this is done, consider the most basic property of all neural cells, namely, that they are threshold elements. Neurons generate standard action potentials only when the membrane is depolarized to the threshold value. Imagine that a neuron receives a suprathreshold signal (Figure 2A); the neuron will generate action potentials at the highest possible frequency as long as the signal stays above the threshold. It will become insensitive to any other inputs. Imagine now that a neuron is depolarized below the threshold (Figure 2B and C). In this case, the neuron will be sensitive to other inputs, for example those from peripheral sensory receptors, and will respond stronger to them for larger initial depolarization magnitudes (compare panels B and C in Figure 2). For a motoneuron receiving both descending and length-sensitive reflex inputs, control with subthreshold depolarization effectively defines a magnitude of muscle length when the neuron starts to generate action potentials during very slow muscle stretch – threshold of the tonic stretch reflex, λ (Figure 2D).

Figure 2.

Imagine an alpha-motoneuron receiving excitation from two sources, central and reflex (the middle insert). A: If its membrane is depolarized above the threshold, it would generate action potentials (AP) at the highest possible frequency; B and C: If the membrane is depolarized below the threshold, it would generate potentials at a frequency defined by the reflex input (length-sensitive), lower in B compared to C. D: The dependence of active muscle force (F) on muscle length (L). The muscle starts generating force at a length corresponding to the threshold of the tonic stretch reflex (λ). It reaches an equilibrium point (EP) when its force is equal in magnitude to the external load.

This method of control has three important advantages. First, it couples the neural world and the mechanical world without any computations. Indeed, the same parameter, λ, is expressed in both millivolts (neuronal depolarization) and meters (tonic stretch reflex threshold). Second, it uses a parameter of a reflex-defined dependence between muscle force and length, namely its threshold (“zero length”). In other words, the mechanism of tonic stretch reflex defines a new body-specific physical law: a relation between two physical variables, forc e and length, with a parameter λ. Third, it represents an example of dealing with an apparent problem of redundancy. Indeed, each muscle is i nnervated by numerous motoneurons so that any given level of its activation can be achieved with an infinite number of combinations of recruited motor units and their firing frequenci es. If an average level of subthreshold depolarization of a pool is defined, the tonic stretch reflex naturally stabilizes an equilibrium state of the s ystem characterized by a combination of musc le length and force counterbalancing the exte rnal load.

Biomechanical methods in motor control

Applications of mechanical analysis in motor control studies are many and varied. Goniometers, accelerometers, motion analysis systems, force platforms, force/moment miniature sensors and many other devices sensitive to mechanical variables are used in studies of the neural control of posture and movement. I am going to review here a couple of less well-known examples when biomechanical methods have been used, in particular, to discover “hidden” parameters manipulated by the controller during voluntary movements.

Reconstruction of referent coordinates

According to the idea of control with referent coordinates, the neural control of a single muscle can be described with time changes of a single parameter, λ (as in the classical equilibrium-point hypothesis, Feldman, 1966, 1986). The control of a simple one degree-of-freedom joint crossed by two muscles, an agonist-antagonist pair, can be described with two parameters, two λs for the opposing muscles (Figure 3). Equivalently, two different parameters can be used associated with reciprocal activation of the muscles and their coactivation. These have been addressed as r-command (the mid-point between the two λs) and c-command (the range of joint angles where both muscles are active), respectively (Figure 3; Feldman, 1980). While both commands are measured in spatial units (units of muscle length or joint rotation), they effectively define the location (r-command) and slope (c-command) of the force-length joint characteristic (shown with the thick, solid line in Figure 3).

Figure 3.

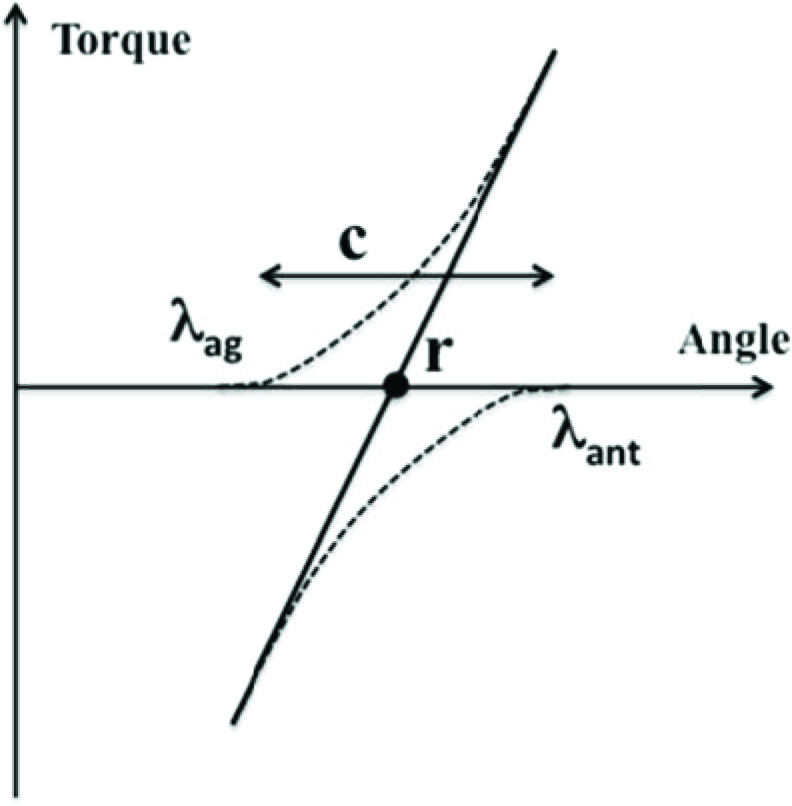
Two muscles crossing a joint, an agonist and an antagonist, produce joint torque in opposite directions (negative for the antagonist). Their control can be described with two λ_s, λ_ag and λ_ant or, alternatively, with r-command (the mid-point between λ_ag and λ_ant) and c-command (the range within which both muscles are active).

It has been assumed that joint movements are controlled with time profiles of the r- and c-commands, while such variables as joint torque, joint angle and muscle activation patterns emerge given the external forces. Biomechanical methods were used to reconstruct the hypothetical r(t) and c(t) time profiles.

The idea of the method is relatively simple. Assume that a person performs a series of trials at the same easy, well-learned task. It is reasonable to assume that each trial is performed using the same r(t) and c(t) commands. If the external torque applied to the joint is changed slowly and unexpectedly in one of the trials, the joint trajectory is expected to change (see Figure 4, dashed lines). Assume now that the subject has been trained to ignore such smooth changes in the external torque and is not correcting the ongoing movement (still using the same r(t) and c(t)). A number of trials are recorded with different directions and magnitudes of external torque change. Now, if one measures the joint angle and computes muscle torque in individual trials at the same phase of the movement (ϕ in Figure 4), the data are expected to fit a line, the torque-angle joint characteristic similar to the one illustrated in Figure 3. The intercept of the line will correspond to the r-command at the given movement phase, while the slope will reflect the c-command. This procedure can be repeated across phases resulting in samples of the r- and c-commands, which can be interpolated to produce r(t) and c(t) time functions.

Figure 4.

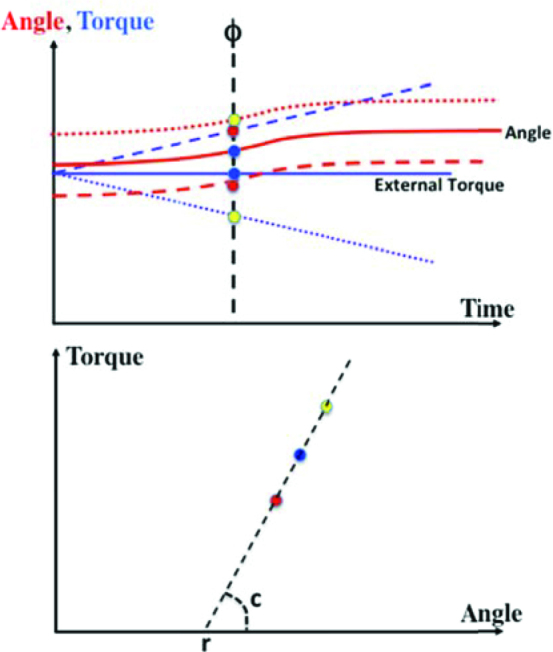
An illustration of experiments with reconstruction of r(t) and c(t) time profiles. The subject performs a simple movement against a constant external torque (solid lines). In some trials the external torque changes smoothly leading to different trajectories (dashed lines). If the subject is not reacting to these perturbations, points on the torque-angle plane measured in different trials at the same phase (the points in the two panels are color-matched) should be on a straight line (bottom panel). Its intercept is r, while its slope reflects c at that particular phase.

This method has been applied to discrete single-joint movements over different distances and at different speeds (Latash and Gottlieb, 1991, 1992), as well as to cyclical joint movements at different frequencies (Latash, 1992). It was also modified to be applicable to two-joint actions (Latash et al., 1999) and, most recently, to movements of the hand grasping an object (Ambike et al., 2015).

It is obvious to any expert in biomechanics that the application of this method hinges on accurate measurement of the joint angle (which is not problematic) and accurate estimation of muscle torque (which is). Indeed, even if a joint is modeled as a second-order linear system (which is already a dubious assumption, see earlier in the paper), its damping coefficient is unknown. Experimental estimations of damping have provided coefficients that vary within a wide range (reviewed in Zatsiorsky, 1997). While most of them suggest that human joints are underdamped (Bennett, 1993; Cannon and Zahalak, 1982; Lacquaniti et al., 1992), all these estimates may be unreliable, in particular because they do not consider damping provided by the velocity-sensitive response of the muscle spindles (see Gribble et al., 1998). Hence, specific shapes of the r(t) and c(t) reconstructed in experiments, in particular, the so-called N-shaped equilibrium trajectories during fast movements (Latash and Gottlieb, 1991, 1992) may result from the inadequate estimates of joint damping.

A recent study of hand movements used a similar method and explored a wide range of damping coefficients (Ambike et al., 2015). It even considered fractional power damping as suggested in earlier studies (Gielen and Houk, 1984). Second-order models provided the best fit to the data with very low (in fact, zero) damping values. This may mean that either the human effectors are truly underdamped or that second-order models are absolutely inapplicable to analysis of such movements.

Analysis of synergies

Another group of recent studies have used biomechanical methods to explore motor coordination within the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner, 1999; reviewed in Latash et al., 2007; Latash, 2008, 2010). The UCM hypothesis is based on the notion of task-specific stability of biological movements involving apparently redundant (actually, abundant!) sets of elemental variables (Schöner, 1995). Note that stability is crucial for everyday movements given that they are performed in the poorly predictable environment characterized by frequent and unexpected changes in the external forces (e.g., stepping on a pebble, picking an object with unknown weight, being bumped in a crowded place, standing in a vehicle that suddenly starts to move, etc.).

Neural organizations ensuring stability of performance with respect to salient variables by typical multi-degree-of-freedom systems have been addressed as synergies (Latash et al., 2007). There is quite a bit of confusion with this term. The same word has been used in clinical studies with a negative connotation implying stereotypical motor patterns interfering with purposeful movements in some groups of patients, in particular those after a stroke (Bobath, 1978; DeWald et al., 1995). The same word has also been used to address groups of variables (kinematic, kinetic and electromyographic) that show parallel scaling during performance of a task and/or with changes in task parameters (Latash and Zatsiorsky, 2016; Tresch and Jarc, 2009). Uniting elements into such synergies has been assumed to reduce the number of degrees-of-freedom and alleviate the problem of dealing with motor redundancy. Since, as mentioned earlier, redundancy is not a problem for the central nervous system, we prefer to use synergy in relation to action stability.

Imagine that a person performs a series of movements trying to be consistent across trials. Each trial will start from a somewhat different initial state of the system because of unavoidable variation in both mechanical and neural variables (Figure 5). Assume that the system is dynamically stable in some directions and dynamically unstable (or less stable) in other directions. If one records a series of movements, trajectories are expected to diverge in unstable directions and converge in stable ones. Now, if one computes across-trials variance at a certain phase of the movement, variance in unstable directions in expected to be higher than in relatively more stable directions. This illustration shows that analysis of the structure of variance provides a proxy of stability in different directions of the abundant space of elemental variables.

Figure 5.

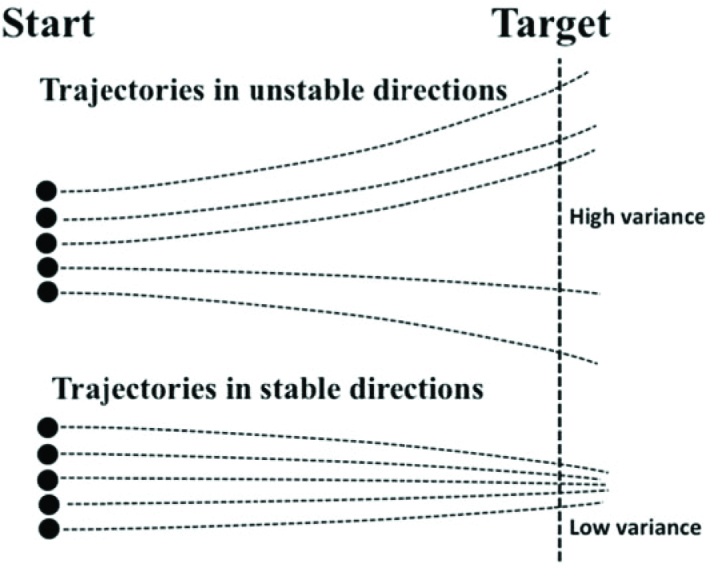
A person performs a series of trials starting from somewhat different initial states (Start). Trajectories are expected to diverge in unstable directions (top lines) and converge in stable ones (bottom lines). Now, if one computes across-trials variance at a certain phase of the movement (e.g., at the Target), variance in unstable directions is expected to be higher than in relatively more stable directions.

This method has been applied to a variety of tasks performed by different populations and analyzed within spaces of different elemental variables (reviewed in Latash, 2008, 2010). In particular, many studies used kinematic (such as joint rotations) and kinetic (such as joint torques and digit forces) variables to perform analyses of the structure of inter-trial variance to estimate stability of specific performance variables to which all the elemental variables contributed. So far, the method has proven to be very productive with the discovery of new phenomena, such as selective stabilization of only some of the performance variables (Scholz and Schöner, 1999; Scholz et al., 2002), anticipatory synergy adjustments (Olafsdottir et al., 2005), the involvement of many body joints in postural sway (Hsu et al., 2007; Scholz et al., 2012), and significant changes in task-specific stability in patients with subcortical disorders (reviewed in Latash and Huang, 2015). The method has also been extended to analyze the phenomenon of motor equivalence, large movements of the high-dimensional system of elemental variables in directions leading to no changes in salient performance variables (Mattos et al., 2011, 2015). Without proper tools supplied by biomechanics, those studies would have been impossible to perform.

Concluding comments

While the recent progress in biomechanics and motor control has been impressive, we are still far from being able to make recommendations for practitioners, such as physical therapists, coaches and physical education teachers. The current established knowledge is meager and the intuition of a good clinician or a good coach typically beats recommendation that can be made by a researcher. This situation will change only after an adequate language to describe biological movement is introduced (cf. Gelfand and Latash, 1998) and laws of nature that describe the interactions both within the body and between the body and the environment are discovered. This is an exciting time for researchers in the fields of biomechanics and motor control that, in my opinion, are inseparable parts of physics of living systems related to the motor function. The fact that the two are still considered separate subjects is an atavism. The two will merge in a near future and the sooner the better.

How to make this happen? There seem to be two main avenues towards this goal. The first is introducing a seamless sequence of courses that teach biomechanics and motor control where issues of biomechanics are considered with an understanding that biological systems are active and issues of motor control are considered based on biomechanics. The second is to run conferences, workshops and series of seminars with balanced representation of both fields. Of course, such changes will take time. So, they have to be started without further delay.

Authors submitted their contribution to the article to the editorial board.