Materials design by evolutionary optimization of functional groups in metal-organic frameworks

Machine learning is used to optimize functional groups of metal-organic frameworks for a specific application.

Abstract

A genetic algorithm that efficiently optimizes a desired physical or functional property in metal-organic frameworks (MOFs) by evolving the functional groups within the pores has been developed. The approach has been used to optimize the CO₂ uptake capacity of 141 experimentally characterized MOFs under conditions relevant for postcombustion CO₂ capture. A total search space of 1.65 trillion structures was screened, and 1035 derivatives of 23 different parent MOFs were identified as having exceptional CO₂ uptakes of >3.0 mmol/g (at 0.15 atm and 298 K). Many well-known MOF platforms were optimized, with some, such as MIL-47, having their CO₂ adsorption increase by more than 400%. The structures of the high-performing MOFs are provided as potential targets for synthesis.

INTRODUCTION

Metal-organic frameworks (MOFs) are a novel class of materials composed of metal clusters and polydentate organic linkers or secondary building units (SBUs) that self-assemble to form crystalline porous networks (1, 2). MOFs have garnered significant attention for a wide range of applications, such as gas separation and storage (3, 4), catalysis (5), and proton-conducting membranes (6). The breadth of applications is largely due to their highly tunable nature. An enormous array of metal clusters and organic groups can be combined to form a nearly limitless number of MOFs with diverse functional properties. These properties can be further tuned by altering the functional groups within the MOF.

Functionalization has been shown to have a marked effect on the properties of an MOF. For example, Deng et al. (7) synthesized an MOF-5 variant with three different functional groups and found it to have a 400% increase in selectivity for CO₂ over CO when compared to the unfunctionalized parent MOF. Using density functional theory to guide their design, Frysali and co-workers (8) found that the addition of a chosen functional group increases CO₂ adsorption significantly in IRMOF-8. There has also been a desire to increase the complexity of functionalizations (9). For example, Garibay and co-workers (10) have developed versatile postsynthetic methodologies and applied them to functionalize IRMOF-3 with five different functional groups (in this work, we consider –H as a distinct functional group), whereas Deng and co-workers (7) have synthesized MOFs with nine different functional groups.

Determining the optimal groups to functionalize an MOF for an application can be challenging and sometimes nonintuitive. For example, Vaidhyanathan and co-workers (11) synthesized an amine-functionalized zinc triazole–oxalate MOF and found it to have excellent low-pressure CO₂ uptake. The group then synthesized a related MOF in which the oxalate anions were replaced with phosphate, thereby giving more amine groups per metal center. Despite having a similar pore size, as well as a higher amine density, a significant decrease in CO₂ uptake was observed, demonstrating the complexity involved when tuning an MOF’s properties via functionalization (12). If 40 functional groups were considered, there would theoretically be 2.56 million (40⁴) distinct functional group combinations possible. Such a search space would be impossible to explore experimentally, and an exhaustive computational screening would be challenging for most properties, particularly if a quantum mechanical calculation is required in the screening process. One approach that has received attention in materials discovery is the use of evolutionary processes (13).

Genetic algorithms (GAs), which are inspired by Darwinian evolution, have been used in efficient optimization of large and complex search spaces where an exhaustive search would be impractical. GAs have been used in computational materials science for a range of applications (14), including ab initio crystal structure prediction (15). Bao et al. (16, 17) recently developed a GA to optimize an MOF’s properties and showed optimization for methane deliverable capacity and surface area. In their work, they used a large precursor library of commercially available molecules to create new organic linkers, which are combined with a set of metal SBUs to form MOFs. A GA is used to optimize the construction of new organic linkers and their combinations with metal SBUs for a given property of the MOF. As pointed out by the authors, there could be difficulties in synthesizing the MOFs with the created linkers (16) because there is no guarantee that the SBUs will self-assemble to form a stable crystalline structure with the proposed structure. This is often the criticism directed toward hypothetical materials that are proposed in silico. Here, to improve synthetic viability, we have developed a GA that will be used with experimentally realized structures; this GA focuses only on optimizing the functionalization of materials. The premise is that modifying existing stable MOFs where the functional groups can be installed either in a presynthetic or in a postsynthetic fashion will enhance the synthetic viability of the predicted materials. We demonstrate that a specialized GA can efficiently evolve the functional groups in MOFs to optimize a desired property, such that only a fraction of the search space needs to be sampled. MOF functionalization GA (or MOFF-GA, as we will term it here) has tailored mating and mutation routines, along with GA parameters that have been optimized to recover the highest-performing MOFs in the search space as potential targets for synthesis. The GA has been validated on a diverse set of 48 MOFs whose complete search space has been evaluated. We further applied MOFF-GA to optimize the CO₂ uptake of 141 experimentally characterized MOFs under conditions relevant to postcombustion CO₂ capture (0.15 atm and 298 K) and have identified hundreds of potentially high-performing targets for synthesis.

MOFF-GA has 13 GA parameters, such as the population size and mutation rates that were optimized to give the highest best-find rate and the number of top 50 MOFs recovered while minimizing the number of unique MOFs sampled. Three different properties [CO₂ uptake, surface area, and parasitic energy (PE)] computed on an assortment of MOFs were used to optimize the parameters. As a result, we consider the default MOFF-GA parameters to be fairly generalized and robust. Full details of the parameterization, implementation, and other computational details are given in Materials and Methods and the Supplementary Materials. We only highlight a few important features here. The first challenge of successfully applying a GA to the specific problem is to define a suitable chromosome representation of the search space in which desirable traits can be inherited. The chromosome representation or genome can strongly affect the optimization efficiency. The functionalizable sites that are equivalent are first identified and numerically labeled, as shown in Fig. 1A for the organic SBUs of ZBP [Zn2(1,4-benzenedicarboxylate)2(pyrazine)]. Here, equivalent functionalization sites are determined from symmetry and refer to those that will enable the SBUs to be reversed (or rotated) to give a structure with the same connectivity. This equivalence is used to limit the search space to structures that are considered more synthetically feasible. The chromosome in MOFF-GA is simply the sequence of equivalent functionalization sites and their associated functional groups. Figure 1B gives an example of a chromosome for ZBP. When creating a structure, MOFF-GA performs a partial conformation search to determine whether the functionalization is sterically feasible. If it is not, then the structure is discarded, thereby causing the mechanism that created the chromosome to repeat until a viable structure is made. MOFF-GA contains a unique mutation algorithm that, when a mutation occurs, it will replace the functional group with a chemically similar functional group. The chemical similarity is based on electrostatic potential (ESP), van der Waals potential (VdWP), and steric availability around the functional group (further details are given in Materials and Methods and the Supplementary Materials). All structures are geometry-optimized with the universal force field (UFF) (18) (including cell vectors) to alleviate steric clashes during functional group insertion. CO₂ adsorption properties were determined from grand canonical Monte Carlo (GCMC) simulations using the UFF and ab initio–fitted MEPO (MOF electrostatic potential–optimized)–charge equilibration (QEq) charges (19) for the framework atoms. The gas adsorption simulations have been shown to accurately reproduce experimental results, such as CO₂ adsorption (11, 12, 20).

Fig. 1. Chromosome representation and mating.

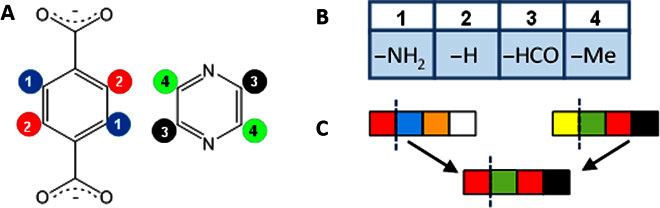
(A) The organic SBUs of the MOF ZBP with the functionalizable positions highlighted. (B) Example chromosome of ZBP. (C) Schematic of the one-cut mating process.

RESULTS

To demonstrate a typical GA run, we optimized the four functional groups in ZBP for CO₂ uptake capacity at 0.15 atm and 298 K. Here, we used 28 common functional groups (table S9); for ZBP’s 4 functional groups, there are theoretically 614,656 combinations possible. However, only 96,156 combinations were found to be sterically viable. This number is small enough that the CO₂ uptake of all viable structures has been calculated to validate the GA. It should be noted that, before the optimization, it is not known which combinations are sterically viable, and, as a result, the GA is still searching the complete search space of 614,656 combinations.

Figure 2 shows the progress of a typical MOFF-GA run in which the CO₂ uptake capacity is optimized in the MOF ZBP. The average CO₂ uptake capacity of the population (size, 113) and the uptake capacity of the best individual are plotted as a function of the generation. Figure 2 reveals that the fittest individual in the population rapidly increases and does not improve after seven generations. In this particular run, MOFF-GA does find the global optimum, which has an exceptional uptake of 4.2 mmol/g—a 4.8-fold increase over the parent MOF.

Fig. 2. MOFF-GA results.

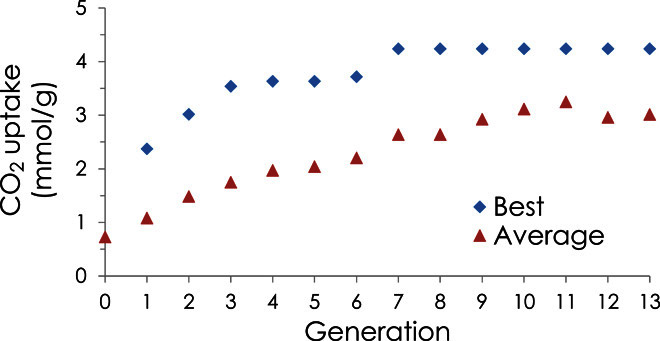
Population average and best individual CO₂ uptake (at 0.15 atm and 298 K) as a function of the generation during an MOFF-GA run for the optimization of the MOF ZBP. The generation zero uptake is that of the unfunctionalized MOF.

Table 1 shows relevant per-run optimization statistics based on 1000 GA runs on ZBP with different random seeds. The “best-find rate” provides the percentage of GA runs that locate the true global optimum. The average rank of the top MOF from a GA run is given as “rank of best,” where the closer to 1 a rank is, the better. The “number of top 50” refers to the average number of the top 50 MOFs that the GA can locate in a run. The “structures sampled” gives the average number of viable structures (and percentage of all possible viable structures) that are sampled in each run. In practice, GAs are typically run multiple times (three to five) on the same problem with different random seeds. If one were to run MOFF-GA five times to optimize the functional groups of ZBP for CO₂ uptake capacity, it would find the top-ranked structure 99.9% of the time and recover 33 of the top 50 MOFs on average while only sampling a total of 4553 unique structures.

Table 1. MOFF-GA results for ZBP.

Averaged statistic of 1000 GA runs for the functional group optimization of ZBP for different properties. The percentages under the Structures sampled column are a fraction of the total number of sterically viable structures (96,156).

Property optimized	Best-find rate (%)	Rank of best	Number of top 50	Structures sampled	Functional groups of best
CO2 uptake at 0.15 atm CO2 and 298 K	81	1.6	20.9	1069 (1.1%)	HCO, H, HCO, CH=CH2
Volumetric surface area	68	1.9	19.8	1263 (1.31%)	H,H, OPr, H
Parasitic energy	67	2.5	14.7	1519 (1.6%)	NO2, H, OH, HCO

Large surface areas are often desired in nanoporous materials. Table 1 shows the optimization statistics of ZBP for the purely geometric property of the volumetric surface area. In this case, the best-find rate of the GA is not as favorable. We attribute this to the fact that the optimal solutions can be single large functional groups, such as propyl ether, or multiple smaller functional groups having similar areas. Although the best-ride rate is not as favorable, the average rank and the number of top 50 found are similar to those found for the CO₂ uptake optimization. In pragmatic terms, finding the single best functionalization is not as important as finding a number of the top candidates.

Multiproperty fitness functions can also be optimized. To demonstrate this, we optimize the parasitic energy, which gives the energetic cost of CO₂ capture under specific adsorption and desorption conditions (21, 22). It can be defined in terms of the uptake capacities of CO₂ under adsorption (0.15 atm and 298 K) and desorption conditions (0.7 atm and 413 K), the heats of adsorption, the CO₂/N₂ adsorption selectivity, and the latent heat capacity of the MOF. All of these quantities can be evaluated with the same GCMC simulations used to calculate the CO₂ uptake, with the exception of the heat capacity, which we fix to a typical value of 1.0 kJ/kg∙K. The parasitic energy can have opposing terms similar to those found in multiobjective optimizations that must be balanced during the optimization. Specifically, a high CO₂ uptake capacity is often associated with a high binding energy or heat of adsorption (HoA), and although a high uptake is good for the parasitic energy, a high HoA is detrimental to it. Table 1 reveals that the parasitic energy is more challenging for MOFF-GA to optimize than either the CO₂ uptake capacity or the surface area for ZBP. Nevertheless, the optimization metrics are still quite favorable, and running MOFF-GA five times would recover the best-performing structure 99.0% of the time and 33 of the top 50 MOFs on average.

To examine how broadly applicable MOFF-GA is to a variety of MOFs and different-sized search spaces, we have optimized the parasitic energy of a diverse set of 48 experimentally characterized MOFs. The averaged optimization metrics for 25 two-site and 18 three-site MOFs are given in Table 2, whereas the metrics for MOFs with four or more sites are given individually. The complete search space for all of these systems has been evaluated (297,125 viable, 19 million in total) for validation purposes.

Table 2. MOFF-GA results for parasitic energy.

Averaged statistics of 1000 GA runs for the functional group optimization of MOFs for parasitic energy. Viable structures are the total number of sterically viable structures. The percentage under the Structures sampled column is an average of the fraction of the total number of viable structures.

MOF	Sites	Viable structures	Best-find rate (%)	Rank of best	Number of top 50	Structures sampled
Two-site: average of 25 MOFs (alternate GA parameters)	2	361	93 (70)	1.1 (1.6)	43.0 (25.8)	67.8 (32.0%)
Three-site: average of 18 MOFs	3	4,149	76	1.6	28.7	22.9
MEKDUC*	4	5,808	75	1.6	29.4	9.9
UTEXAT* (four of five sites)	4	20,825	84	1.3	34.0	4.3
FUNBEW-Br*	4	32,215	31	5.9	8.6	3.8
UTEXAT*	5	33,072	90	1.2	20.3	2.8

*Cambridge Structural Database identifier.

Two-site MOFs, which have a theoretical search space size of 784, were tested to determine whether the GA would apply to small search spaces (<1000). Table 2 reveals that the optimization metrics are excellent, except that the GA samples 68% of the viable structures in a single run on average. Thus, it only makes sense to run the GA once, but this does not result in a significant reduction of sampling compared to a complete scan. Because the GA parameters were optimized using test sets with large search spaces, we reoptimized the GA parameters using only two-site MOFs. The optimization metrics with this alternate set of GA parameters is given in parentheses in Table 2. With the two-site GA parameters, the number of unique structures sampled is halved, but there is also a notable reduction in the best-find rate from 93 to 70%. In some scenarios, it may be of value to apply MOFF-GA on small search spaces, for example, when optimizing a property that is very time-consuming to evaluate, such as nonlinear optical properties that require expensive first-principles calculations. In such a case, running MOFF-GA once with the two-site parameters would sample only a third of the search space while still recovering many of the top candidates (on average 26 of the top 50, with a best rank of 1.6).

Eighteen unique three-site MOFs, each having a total search space size of 21,952, have been optimized, the number of viable structures of which ranged from 1054 to 17,514. On average, a single MOFF-GA run would sample 23% of the viable structures with a best-find rate of 76%. Because one typically has an idea of the theoretical search space size beforehand, one could run the GA two or three times for searches whose size is <20,000. Using the averaged statistics, running the GA twice would sample ~40% of the viable structures but would have a 95% chance of finding the top performer. Again, in some usage scenarios, sampling only 40% of the search space would result in worthwhile time savings compared to an exhaustive systematic search.

The benefit of applying the GA becomes readily apparent with four-site and larger search spaces. Table 2 shows the optimization metrics for four- and five-site MOFs for which we have performed a full scan of the search space. If we were to include ZBP (Table 1), the number of viable structures would range from 5808 to 96,156. The optimization statistics are generally very good, and applying MOFF-GA five times will only sample a fraction of the total search space while having a high probability of recovering the top-performing structures. Even with the MOF FUNBEW-Br, which had the lowest optimization statistics found in this study, the application of the GA would be beneficial. Specifically, if one were to apply MOFF-GA five times, one would still recover the top-performing structure 84% of the time, although only 16% of the entire viable search space would be sampled. In addition, after five GA runs, on average, one would recover 27 of the top 50 structures, providing many targets for synthesis.

MOFF-GA has been applied to optimize the CO₂ uptake capacity of an additional 93 experimentally characterized MOFs, including several MOFs whose search space is too large to evaluate completely (>1.7 × 10⁷). Including the 48 MOFs used to validate MOFF-GA, we plot in Fig. 3 the optimized CO₂ uptake of 141 MOFs compared to the CO₂ uptake of the unfunctionalized parent structure. Although a small fraction of MOFs see little to no improvement (mostly small-pore MOFs), there is, on average, a 3.7-fold (1.14 mmol/g) increase in CO₂ uptake upon functional group optimization. We highlight a few well-known MOFs, such as MIL-47 and HKUST-1, which show considerable improvement. With the addition of one functional group, the uptake of MIL-47 increases by 2.74 mmol/g. In addition, 1035 functionalized structures from 23 different parent MOFs were predicted to have a CO₂ uptake capacity of more than 3 mmol/g at 0.15 atm and 298 K. This is deemed high-performing under these conditions, especially considering that none of the parent MOFs have open metal sites, which can enhance the CO₂ uptake through chemisorption (but also make them prone to water degradation). The aldehyde (–HCO) functional group and not the amine group was the most common substituent in the MOFs with uptakes >3 mmol/g. Moreover, of these high-performing MOFs, 85% have only one to three different nonhydrogen functional groups, which enhances the prospect that the MOFs identified could be synthesized. At this point, the practical application of MOFF-GA involves constructing a hypothetical structure and computing the properties. Consequently, the screening results are vulnerable to issues similar to those of other large-scale virtual screening studies in that the structures predicted may be impossible to synthesize or may be structurally different from those made in the laboratory (23, 24). However, because the structures identified in this work are derived from experimentally characterized MOFs, they may be more synthetically accessible compared to purely hypothetical MOFs.

Fig. 3. MOFF-GA results on experimental MOF.

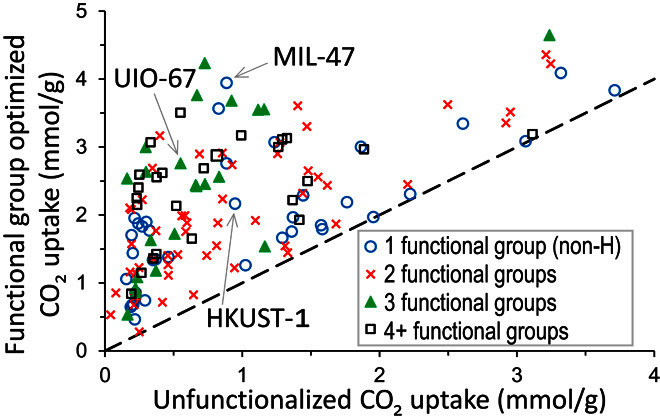
CO₂ uptake at 0.15 atm and 298 K for 141 experimentally characterized MOFs whose functional groups have been optimized with MOFF-GA compared to the uptake of the unfunctionalized parent MOF (dashed line). Data point symbols denote the number of unique, nonhydrogen functional groups in the best structure.

DISCUSSION

Functionalization has always been considered a principal avenue for improving the functional properties of MOFs. Here, we have developed a customized GA to identify the most favorable functionalizations of a parent MOF to optimize a desired functional and/or physical property. MOFF-GA, as we term it, has been validated on a diverse set of 48 MOFs with a range of search space sizes. We demonstrate that MOFF-GA can locate the best structures while sampling only a small fraction of the search space. MOFF-GA is particularly powerful when applied to large search spaces but can still be beneficial when applied to small search spaces (<1000), particularly if the property being optimized is time-consuming to evaluate. The CO₂ uptakes of 141 experimentally characterized parent MOFs have been optimized, resulting in 1035 functionalized derivatives of these MOFs being identified with exceptional uptakes of >3 mmol/g at 0.15 atm and 298 K. All of these structures are provided in the Supplementary Materials to allow researchers to browse and identify potential synthetic targets. In total, the CO₂ uptake of 581,278 unique structures has been calculated to screen a search space of more than 1.64 trillion structures. More than 20 well-known MOFs were optimized for CO₂ uptake, with MIL-47 reaching nearly a capacity of 4 mmol/g upon functionalization. Although some of these structures may be challenging or even impossible to synthesize, the approach yields many high-performing structures, which can then be examined by researchers to identify the best potential synthetic targets. MOFF-GA demonstrates an efficient method for predictive high-performance materials design that should be applicable not only to MOFs but also to the functionalization of other classes of materials, such as covalent organic frameworks and porous polymer networks (25). We also note that properties aside from those evaluated in this work can also be included in the fitness function and optimized as long as they can be accurately computed, including the synthetic accessibility (26).

MATERIALS AND METHODS

Our GA followed most of the same procedures as other GAs. An initial set of individuals were randomly created; the number of members of the set is known as the population. A set of individuals at a given time is known as a generation. All individuals in the generation were evaluated for their fitness, such as CO₂ uptake. The next generation was constructed from the previous one with mating and mutation mechanisms. Our GA used elitism, which carried forward a fraction of the top-performing individuals from one generation into the next generation with no modification. The fraction of top performers carried forward is known as the elite. The population size and the elite fraction are adjustable parameters of the optimization algorithm.

Another challenge in applying a GA involved developing mating and mutation schemes that allowed the desirable traits to be passed onto subsequent generations while still allowing for a broad sampling of the search space. In MOFF-GA, the mating scheme used consisted of cutting the chromosome of each parent at the same point and combining opposite sides of the chromosome from each parent to form the child chromosome. The cut position was determined randomly, and the process is shown schematically in Fig. 1C. A similar two-cut mating scheme was also used.

After mating occurred to create a new generation, each individual had a chance, governed by the mutation rate parameter, to undergo a mutation. Two mutation mechanisms were used in MOFF-GA. The first was a swap mutation, where two randomly chosen functional groups of a chromosome were exchanged. The second mutation involved randomly replacing one group with either a similar (that is, methyl for ethyl) or a dissimilar functional group, where the use of a similar or dissimilar group was chosen randomly according to the similarity probability parameter. The higher the similarity probability, the more likely a chemically similar functional group will be chosen. Chemical similarity was determined by three properties: the ESP, the VdWP, and steric hindrance. For all functional groups, the groups were aligned as if attached to a benzene ring, and all of the properties were calculated on identical three-dimensional grids. ESPs were calculated using QEq atomic charges on the functional group with a point charge probe. The VdWPs were calculated using a Lennard-Jones potential and a carbon probe. Steric hindrance was decided with a binary output using the VdWP. If the VdWP at a grid point was 0 or greater, it was set as sterically unavailable and assigned a value of 1. If the VdWP was below 0, it was sterically available and assigned a value of 0. To calculate the similarity between two functional groups, we used a continuous Tanimoto coefficient (27), which returns a score from 0 (maximum dissimilarity) to 1 (the same) for any pair of groups. The value of each property at each grid point was used to evaluate the Tanimoto coefficient. For each pair of functional groups, the calculated Tanimoto coefficient was used to determine whether the pair was similar or dissimilar using a similarity threshold parameter.

During the optimization process, once the top-performing individual had remained constant for a set number of generations (currently three), MOFF-GA entered a stagnation phase. During the stagnation phase, MOFF-GA used three methods to create new individuals: mutating the best, random creation, and normal mating. When mutating the best, individuals were created, which differed from the best performer by one functional group only. All combinations of these individuals were created randomly over stagnant generations and tested for their performance. A fraction of the population of each generation, determined by the best mutated parameter, was reserved for these individuals. Random creation, during the stagnation, added completely randomly made individuals for each generation of the stagnation phase. The amount of randomly created individuals for each generation was set by the random mutated parameter. The remaining populations were created using the normal mating scheme.

MOFF-GA has two convergence criteria that must be met before the optimization is stopped: First, the top-performing individual must remain the same for a certain number of generations (currently five), and second, all individuals created in the aforementioned stagnation phase, which differ by only one functional group from the top performer, must be tested. Once these two criteria are met, MOFF-GA is considered complete. Full details of MOFF-GA are given in the Supplementary Materials, along with a full description of all 13 GA parameters, their optimized values, and details of how the parameters were optimized.

Gas adsorption calculations were performed using an in-house GCMC code based on the DL_POLY 2 molecular dynamics package (28). Nonbonding interactions were calculated with a Lennard-Jones potential using parameters for the framework atoms taken directly from the UFF (18) with Lorentz-Berthelot mixing rules for cross-terms. Electrostatics were based on partial atomic charges calculated by QEq using the MEPO-QEq parameters (19), which were fit to reproduce the ESP obtained from REPEAT atomic partial charges (29). The CO₂ molecules were modeled using the force field developed by García-Sánchez et al. (30), and the N₂ molecules were modeled using the TraPPE force field parameters (31).

All GCMC simulations consisted of 30,000 cycles of equilibration and 30,000 cycles of production. One cycle consisted of n trial moves, where n is equal to the number of guest molecules in the system at that time. All simulations included random insertion, deletion, and translation moves of molecules with equal probabilities. Atoms in the framework were held fixed at their crystallographic positions. A Lennard-Jones cutoff distance of 12.5 Å was used for all simulations, and a supercell was constructed for each structure that satisfied the minimum image criterion. The ideal gas law was assumed when computing the chemical potential in GCMC simulations. Surface area calculation was performed using a helium probe (1.0 Å) in the Zeo++ software package (32).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/11/e1600954/DC1

Details of the GA

GA parameters

Parameter optimization

MOFF-GA parameter values

Structure preparation and construction

Molecular simulations

Parasitic energy

Top-performing structures

fig. S1. Example of the application of a functional group code to the unfunctionalized SBU of the parent MOF.

fig. S2. Schematic of the one-cut mating process.

fig. S3. Schematic of the two-cut mating process.

fig. S4. Schematic of swapping mutation.

fig. S5. Fitted transformation function (blue dotted line) used in GAPI (genetic algorithm performance indicator) for the best-find rate.

fig. S6. Fitted transformation function (blue dotted line) used in GAPI for the top 50 performers recovered.

fig. S7. Fitted transformation function (blue dotted line) used in GAPI for unique MOFs tested for large search space (three or more sites) MOFs.

fig. S8. Fitted transformation function (blue dotted line) used in GAPI for unique MOFs tested for two-site MOFs.

fig. S9. Linker symmetry.

table S1. Scaling functions used for fitness.

table S2. Description of the MOFF-GA optimization parameters.

table S3. Values used to fit transformation function (eq. S2) of performance properties.

table S4. Fitted values used in eq. S2 for each performance properties. R² values are calculated using table S3 values.

table S5. Sterically viable structures for training MOFs.

table S6. Parameters used by MOFF-GA that were optimized.

table S7. Terms used in parasitic energy with a brief description.

table S8. Functionalized MOFs with CO₂ uptake greater than 3 mmol/g with the corresponding functional groups.

table S9. Details of functional group codes and their associated structure.

References (33–39)